5.3: Prueba de la fórmula integral de Cauchy

Última actualización
Guardar como PDF

Page ID: 109834

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema útil

Antes de probar el teorema necesitaremos un teorema que sea útil por derecho propio.

Teorema$\PageIndex{1}$: A second extension of Cauchy's theorem

Supongamos que$A$ es una región simplemente conectada que contiene el punto$z_0$. Supongamos que$g$ es una función que es

Analítica en$A$ - {$z_0$}
Continuo encendido$A$. (En particular,$g$ no por debajo de arriba en$z_0$.)

Entonces

\[\int_{C} g(z)\ dz = 0\]

para todas las curvas cerradas$C$ en$A$.

Prueba

La versión extendida del teorema de Cauchy en las notas del Tema 3 nos dice que

\[\int_C g(z)\ dz = \int_{C_r} g(z)\ dz,\]

donde$C_r$ es un círculo de radio$r$ alrededor$z_0$.

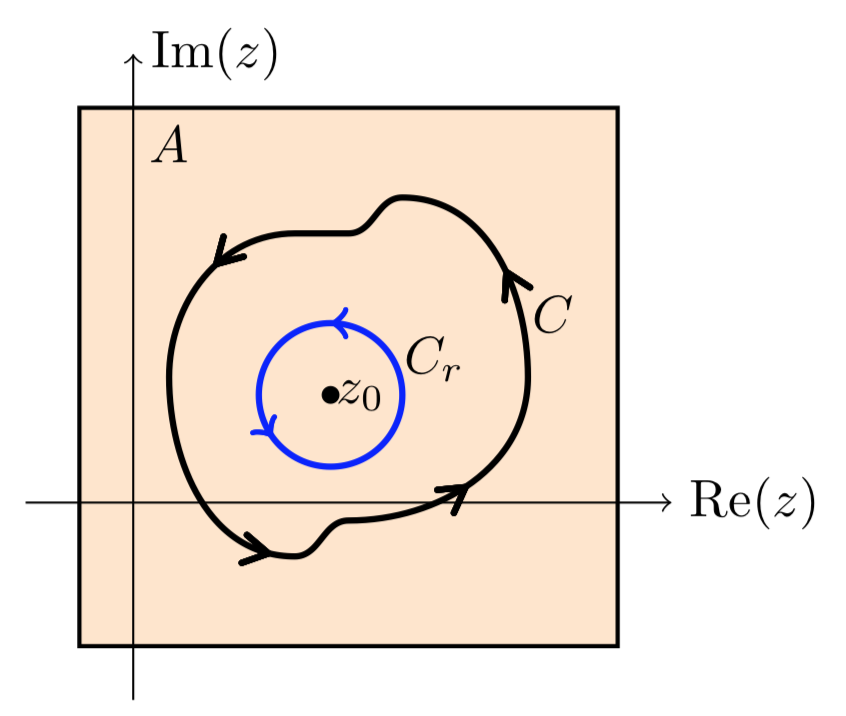
$2020-09-08 4.42.33.png$

Ya que$g(z)$ es continuo sabemos que$|g(z)|$ está acotado por dentro$C_r$. Diga,$|g(z)| < M$. El corolario de la desigualdad triangular dice que

\[|\int_{C_r} g(z)\ dz| \le M \text{ (length of } C_r) = M2 \pi r.\]

Ya que$r$ puede ser tan pequeño como queramos, esto implica que

\[\int_{C_r} g(z) \ dz = 0.\]

Nota

Usando esto, podemos demostrar que$g(z)$ es, de hecho, analítico en$z_0$. La prueba será la misma que en nuestra prueba del teorema de Cauchy que$g(z)$ tiene un antiderivado.

Prueba de la fórmula integral de Cauchy

Reiteramos la fórmula integral de Cauchy a partir de la Ecuación 5.2.1:$f(z_0) = \dfrac{1}{2\pi i} \int_C \dfrac{f(z)}{z - z_0} \ dz$.

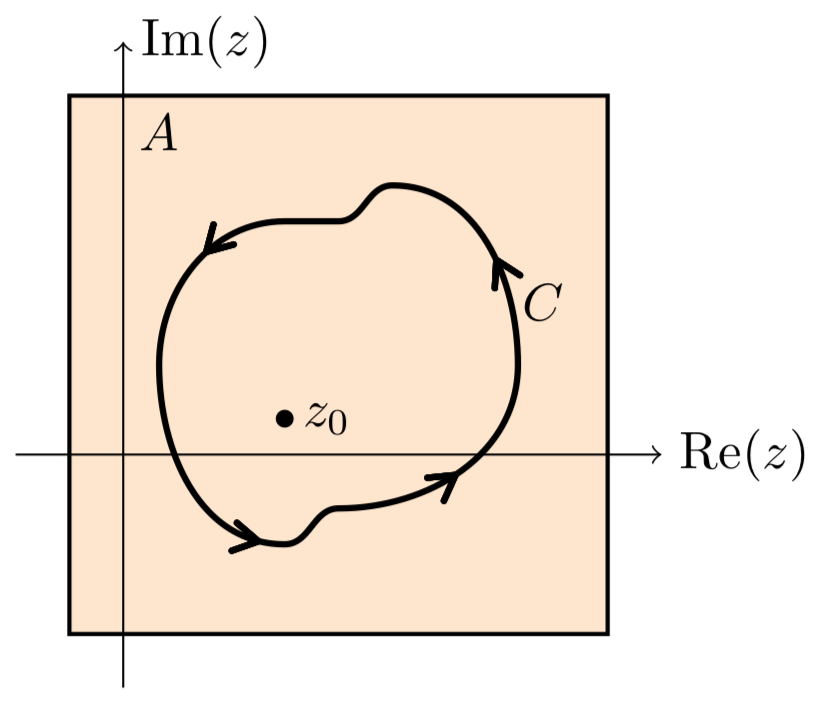
$2020-09-08 4.49.07.png$

$Proof$. (de la fórmula integral de Cauchy) Utilizamos un truco que es lo suficientemente útil como para que valga la pena recordarlo. Let

\[g(z) = \dfrac{f(z) - f(z_0)}{z - z_0}.\]

Ya que$f(z)$ es analítico en$A$, sabemos que$g(z)$ es analítico en$A - \{z_0\}$. Dado que el derivado de$f$ existe en$z_0$, sabemos que

\[\lim_{z \to z_0} g(z) = f'(z_0).\]

Es decir, si definimos$g(z_0) = f'(z_0)$ entonces$g$ es continuo en$z_0$. De la extensión del teorema de Cauchy justo arriba, tenemos

\[\int_{C} g(z)\ dz = 0, \text{ i.e. } \int_C \dfrac{f(z) - f(z_0)}{z - z_0} \ dz = 0.\]

Así

\[\int_{C} \dfrac{f(z)}{z - z_0}\ dz = \int_C \dfrac{f(z_0)}{z - z_0}\ dz = f(z_0) \int_C \dfrac{1}{z - z_0} \ dz = 2\pi i f(z_0).\]

La última igualdad se desprende de nuestra, a estas alturas, bien conocida integral de$1/(z - z_0)$ en un bucle alrededor$z_0$.