2.12: Diferenciación Implícita y Tasas Relacionadas
- Page ID
- 110593
Diferenciación implícita
En nuestro trabajo hasta ahora, las funciones que necesitábamos diferenciar se daban explícitamente, como\( y=x^2+e^x \), o era posible obtener una fórmula explícita para ellas, como resolver\( y^3-3x^2=5 \) para obtener\( y=\sqrt[3]{5+3x^2} \). A veces, sin embargo, tendremos una ecuación relativa\(x\) y\(y\) que es difícil o imposible de resolver explícitamente para\(y\), tales como\( y+e^y=x^2 \). En cualquier caso, todavía podemos encontrar\(y' = f'(x)\) mediante el uso de diferenciación implícita.
La idea clave detrás de la diferenciación implícita es asumir que\(y\) es una función de\(x\) aunque no podamos resolver explícitamente para\(y\). Esta suposición no requiere ningún trabajo, pero hay que tener mucho cuidado para tratar\(y\) como una función cuando diferenciamos y usar la Regla de Cadena.
Supongamos que\(y\) es una función de\(x\). Calcular
- \( \frac{d}{dx}\left( y^3 \right) \)
- \( \frac{d}{dx}\left( x^3y^2 \right) \)
- \( \frac{d}{dx}\left( \ln(y) \right) \)
Solución
- Necesitamos la regla de la cadena ya que y es una función de x:\[ \frac{d}{dx}\left( y^3 \right)=3y^2\frac{dy}{dx}\overset{\text{or}}{=}3y^2y' \nonumber \]
- Necesitamos usar la regla del producto y la regla de la cadena:\[ \begin{align*} \frac{d}{dx}\left( x^3y^2 \right) & = x^3\frac{d}{dx}\left( y^2 \right)+y^2\frac{d}{dx}\left( x^3\right) \\ & = x^32y\frac{dy}{dx}+y^23x^2 \\ \overset{\text{or}}{=}& 2x^3yy'+3y^2x^2 \end{align*} \nonumber \]
- Sabemos\( \frac{d}{dx}\left( \ln(x) \right) =\frac{1}{x} \), entonces usamos eso y la Regla de la Cadena:\[ \frac{d}{dx}\left( \ln(y) \right)=\frac{1}{y}\cdot y' \nonumber \]
Determinar\(y'\), differentiate each side of the defining equation, treating \(y\) as a function of \(x\), and then algebraically solve for \(y'\).
(El último ejemplo en el siguiente video se vuelve bastante desordenado — no te preocupes demasiado si no puedes seguir todas las simplificaciones al final).
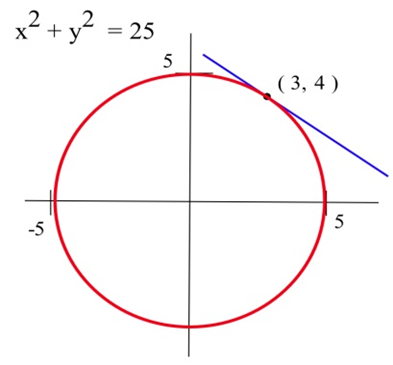
Encuentra la pendiente de la línea tangente al círculo\(x^2 + y^2 = 25\) en el punto (3,4) usando diferenciación implícita.
Solución
Diferenciamos cada lado de la ecuación\(x^2 + y^2 = 25\) y luego resolvemos para\(y'\):\[ \begin{align*} \frac{d}{dx}\left(x^2+y^2\right) & = \frac{d}{dx}(25)\\ 2x+2yy' & = 0 \end{align*} \nonumber \]
Resolviendo para\(y'\), tenemos\( y'=-\frac{2x}{2y}=-\frac{x}{y} \), y, en el punto (3,4),\[y'=-\frac{3}{4}.\nonumber \]
En el ejemplo anterior, hubiera sido fácil de resolver explícitamente para\(y\), y luego podríamos diferenciar\(y\) para obtener\(y'\). Debido a que podíamos resolver explícitamente para\(y\), teníamos una opción de métodos para calcular\(y'\). A veces, sin embargo, no podemos resolver explícitamente\(y\), y la única manera de determinar\(y'\) es usar la diferenciación implícita.
Tarifas Relacionadas
Si varias variables o cantidades están relacionadas entre sí y algunas de las variables están cambiando a una tasa conocida, entonces podemos usar derivadas para determinar qué tan rápido deben estar cambiando las otras variables.
Aquí hay un enlace a los ejemplos utilizados en los videos de esta sección: Tarifas relacionadas.
Supongamos que la frontera de un pueblo es aproximadamente circular, y el radio de ese círculo ha ido aumentando a una tasa de 0.1 millas cada año. Descubre qué tan rápido ha ido aumentando el área del pueblo cuando el radio es de 5 millas.
Solución
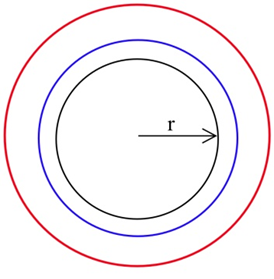
Podríamos obtener una respuesta aproximada calculando el área del círculo cuando el radio es de 5 millas (\( A = \pi r^2 = \pi (5 \text{ miles})^2 \approx 78.6 \text{ miles}^2 \)) y 1 año después cuando el radio es 0.1 pies más grande que antes (\(A = \pi r^2 = \pi (5.1 \text{ miles})^2 \approx 81.7 \text{ miles}^2\)) y luego encontrar\[ \frac{\Delta \text{Area}}{\Delta \text{time}}=\frac{81.7 \text{ mi}^2 - 78.6 \text{ mi}^2}{1 \text{ year}} = 3.1 \text{ mi}^2/\text{yr}.\nonumber \] Esta respuesta aproximada representa el promedio cambio de área durante el periodo de 1 año cuando el radio aumentó de 5 millas a 5.1 millas, y correspondería a la pendiente secante en la gráfica de área.
Para encontrar la respuesta exacta, sin embargo, necesitamos derivados. En este caso tanto el radio como el área son funciones de tiempo:\[r(t)=\text{ radius at time } t \qquad A(t)=\text{ area at time } t\nonumber \]
Sabemos lo rápido que está cambiando el radio, que es una afirmación sobre la derivada:\( \frac{dr}{dt}=0.1\frac{\text{mile}}{\text{year}} \). También sabemos que\(r = 5\) en nuestro momento de interés.
Estamos buscando qué tan rápido está aumentando el área, que es\( \frac{dA}{dt} \).
Ahora necesitamos una ecuación que relacione nuestras variables, que es la ecuación de área:\[A=\pi r^2.\nonumber \]
Tomando la derivada de ambos lados de esa ecuación con respecto a\(t\), podemos usar diferenciación implícita:\[ \begin{align*} \frac{d}{dt}\left( A \right) & = \frac{d}{dt}\left( \pi r^2 \right)\\ \frac{dA}{dt} & = \pi 2r\frac{dr}{dt} \end{align*} \nonumber \]
Enchufar los valores que conocemos\(r\) y\(\frac{dr}{dt}\),\[ \frac{dA}{dt}=\pi 2(5\text{ miles})\left(0.1\frac{\text{miles}}{\text{year}}\right)=\pi\frac{\text{miles}^2}{\text{year}}\nonumber \]
Por lo que el área del pueblo está aumentando aproximadamente 3.14 millas cuadradas al año cuando el radio es de 5 millas.
Cuando se trabaja con un problema de tarifas relacionado,
- Dibuja un cuadro (si es posible).
- Identificar las cantidades que están cambiando, y asignarles variables.
- Encuentra una ecuación que relacione esas cantidades.
- Diferenciar ambos lados de esa ecuación con respecto al tiempo.
- Conecte cualquier valor conocido para las variables o tasas de cambio.
- Resuelve para la tasa deseada.
Una empresa ha determinado la curva de demanda de su producto es\( q=\sqrt{5000-p^2} \), dónde\(p\) está el precio en dólares, y\(q\) es la cantidad en millones. Si las condiciones climáticas están haciendo subir el precio $2 a la semana, encuentra la tarifa a la que la demanda está cambiando cuando el precio es de $40.
Solución
Las cantidades que cambian son\(p\) y\(q\), y asumimos que ambas son funciones del tiempo,\(t\), en semanas. Ya tenemos una ecuación que relaciona las cantidades, por lo que podemos diferenciarla implícitamente. \[ \begin{align*} \frac{d}{dt}(q) & = \frac{d}{dt}\left(5000-p^2\right)^{1/2} \\ \frac{dq}{dt} & = \frac{1}{2}\left(5000-p^2\right)^{-1/2}\frac{d}{dt}\left(5000-p^2\right) \\ \frac{dq}{dt} & = \frac{1}{2}\left(5000-p^2\right)^{-1/2}\left(-2p\frac{dp}{dt}\right) \end{align*} \nonumber \]
Usando la información dada, sabemos que el precio está aumentando en $2 por semana cuando el precio es de $40, dando\( \frac{dp}{dt}=2 \) cuando\(p = 40\). Enchufar estos valores,\[ \frac{dq}{dt} = \frac{1}{2}\left(5000-40^2\right)^{-1/2}\left(-2(40)(2)\right) \approx -1.37 \nonumber \]
La demanda está cayendo 1.37 millones de artículos por semana.
El costo total diario para producir\(x\) artículos en un día es\(TC(x) = 300,000 + 4x + \frac{200,000}{x}\). Si la producción ha ido aumentando 20 artículos al día, encuentre la tasa a la que el costo total diario está aumentando, si actualmente están produciendo 2,000 artículos.
Solución
Las cantidades que cambian son\(x\) y\(TC\), y asumimos que ambas son funciones del tiempo,\(t\), en días. Ya tenemos una ecuación que relaciona las cantidades, por lo que podemos diferenciarla implícitamente. \[ \begin{align*} \frac{d}{dt}(TC) & = \frac{d}{dt}\left(300,000 + 4x + 200,000x^{-1}\right) \\ \frac{d TC}{dt} & = 4\frac{dx}{dt} - 200,000x^{-2}\frac{dx}{dt}\\ \frac{d TC}{dt} & = \left(4 - \frac{200,000}{x^2}\right)\frac{dx}{dt}\\ \end{align*} \nonumber \]
Sabemos que la cantidad producida está aumentando en 20 artículos por semana cuando la producción es de 2,000 artículos, dando\( \frac{dx}{dt}=20 \) cuando\(x = 2000\). Enchufar estos valores,\[ \frac{d TC}{dt} = \left(4 - \frac{200,000}{2000^2}\right)(20) = 79 \nonumber \]
El costo total diario aumenta en $79 cada día.