2.E: La Derivada (Ejercicios)
- Page ID
- 110584
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Ejercicios
Utilice la gráfica para determinar los siguientes límites.
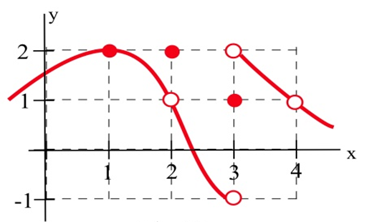
| a.\(\lim_{x \to 1} f(x)\) | b.\(\lim_{x \to 2} f(x)\) |
| c.\(\lim_{x \to 3} f(x)\) | d.\(\lim_{x \to 4} f(x)\) |
Utilice la gráfica para determinar los siguientes límites.
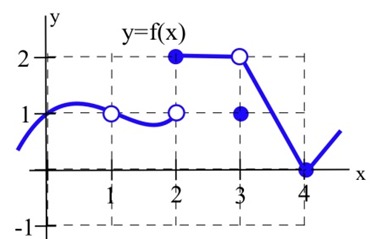
| a.\(\lim_{x \to 1} f(x)\) | b.\(\lim_{x \to 2} f(x)\) |
| c.\(\lim_{x \to 3} f(x)\) | d.\(\lim_{x \to 4} f(x)\) |
Evaluar
| a.\(\lim_{x \to 1} \frac{x^2+3x+3}{x-2}\) | b.\(\lim_{x \to 2} \frac{x^2+3x+3}{x-2}\) |
Evaluar
| a.\(\lim_{x \to 0} \frac{x+7}{x^2+9x+14}\) | b.\(\lim_{x \to 3} \frac{x+7}{x^2+9x+14}\) |
| c.\(\lim_{x \to 4} \frac{x+7}{x^2+9x+14}\) | d.\(\lim_{x \to 7} \frac{x+7}{x^2+9x+14}\) |
¿En qué puntos se muestra la función discontinua?
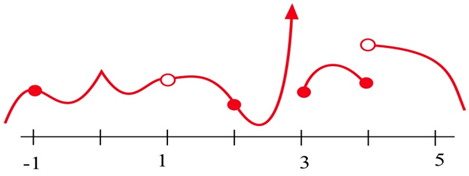
¿En qué puntos se muestra la función discontinua?
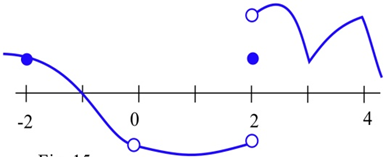
Encontrar al menos un punto en el que cada función no sea continua y establezca cuál de las 3 condiciones en la definición de continuidad se viola en ese punto
| a.\(\frac{x+5}{x-3}\) | b.\(\frac{x^2+x-6}{x-2}\) | c.\(\frac{x}{x}\) |
| d.\(\frac{\pi}{x^2-6x+9}\) | e.\(\ln (x^2)\) |
2.2 Ejercicios
¿Cuál es la pendiente de la línea a través (3,9) y\((x, y)\) para\(y = x^2\) y\(x = 2.97\)? \(x = 3.001\)? \(x = 3+h\)? ¿Qué sucede con esta última pendiente cuando\(h\) es muy pequeña (cercana a 0)? Esbozar la gráfica de\(y = x^2\) para\(x\) cerca de 3.
¿Cuál es la pendiente de la línea a través (—2,4) y\((x, y)\) para\(y = x^2\) y\(x = –1.98\)? \(x = –2.03\)? \(x = –2+h\)? ¿Qué sucede con esta última pendiente cuando\(h \) es muy pequeña (cercana a 0)? Esboce la gráfica de\(y = x^2\) para\(x\) cerca —2.
¿Cuál es la pendiente de la línea a través (2,4) y\((x, y)\) para\(y = x^2 + x – 2\) y\(x = 1.99\)?
\(x = 2.004\)? \(x = 2+h\)? ¿Qué pasa con esta última pendiente cuando\(h\) es muy pequeña? Esbozar la gráfica de\(y = x^2 + x – 2\) para\(x\) cerca de 2.
¿Cuál es la pendiente de la línea a través (—1, —2) y\((x, y)\) para\(y = x^2 +x – 2\) y\(x = –.98\)?
\(x = –1.03\)? \(x = –1+h\)? ¿Qué pasa con esta última pendiente cuando\(h\) es muy pequeña? Esboce la gráfica de\(y = x^2 + x – 2\) para\(x\) cerca —1.
La gráfica de la derecha muestra la temperatura durante un día en Ames.
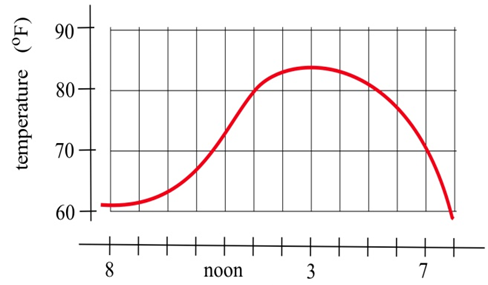
a) ¿Cuál fue el cambio promedio en la temperatura de las 9 de la mañana a la 1 de la tarde?
b) Estimar qué tan rápido estaba subiendo la temperatura a las 10 de la mañana y a las 7 de la tarde?
El gráfico muestra la distancia de un automóvil desde una posición de medición ubicada al borde de una carretera recta.
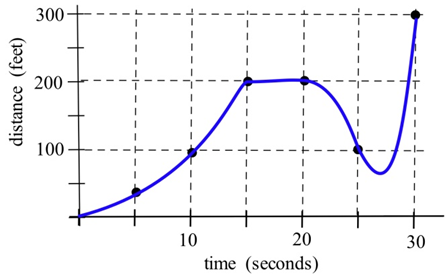
(a) ¿Cuál fue la velocidad promedio del automóvil de\(t = 0\) a\(t = 30\) segundos?
(b) ¿Cuál fue la velocidad promedio del automóvil de\(t = 10\) a\(t = 30\) segundos?
(c) ¿Qué tan rápido viajaba el auto a los\(t = 10\) segundos? en\(t = 20\) s? en\(t = 30\) s?
d) ¿Qué significa la parte horizontal de la gráfica entre\(t = 15\) y\(t = 20\) segundos?
e) ¿Qué\(t = 25\) representa la velocidad negativa a?
El gráfico muestra la distancia de un automóvil desde una posición de medición ubicada al borde de una carretera recta.
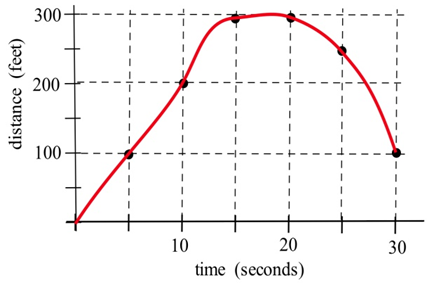
(a) ¿Cuál fue la velocidad promedio del automóvil de\(t = 0\) a\(t = 20\) segundos?
b) ¿Cuál fue la velocidad promedio de\(t = 10\) a\(t = 30\) segundos?
(c) ¿Qué tan rápido viajaba el auto a los\(t = 10\) segundos? en\(t = 20\) s? en\(t = 30\) s?
La gráfica muestra el nivel de habilidad de desarrollo compuesto de maestros de ajedrez a diferentes edades según lo determinado por su desempeño contra otros maestros de ajedrez. (De “Rating Systems for Human Habilidades”, de W.H. Batchelder y R.S. Simpson, 1988. Módulo UMAP 698.)
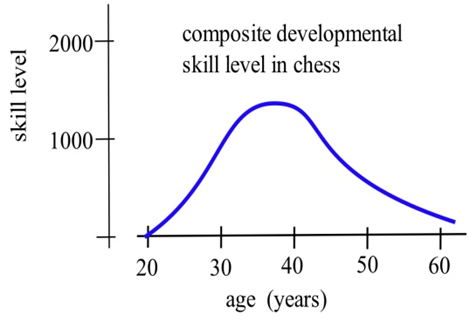
(a) ¿A qué edad el “típico” maestro de ajedrez juega el mejor ajedrez?
b) ¿A qué edad aproximadamente aumenta más rápidamente el nivel de habilidad del maestro de ajedrez?
(c) Describir en palabras el desarrollo de la habilidad “típica” del maestro de ajedrez.
(d) Croquis gráficos que creas que describirían razonablemente los niveles de rendimiento versus la edad de un atleta, un pianista clásico, un cantante de rock, un matemático y un profesional en tu campo mayor.
Utilice la función en la gráfica para rellenar la tabla y luego graficar\(m(x)\).
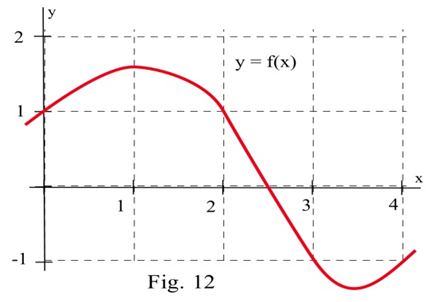
| \(x\) | \(y = f(x)\) | \(m(x) = \)la pendiente estimada de la línea tangente a\(y=f(x)\) en el punto\((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
Utilice la función en la gráfica para rellenar la tabla y luego graficar\(m(x)\).
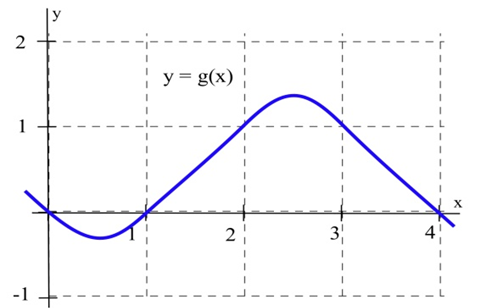
| \(x\) | \(y = g(x)\) | \(m(x) = \)la pendiente estimada de la línea tangente a\(y=g(x)\) en el punto\((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
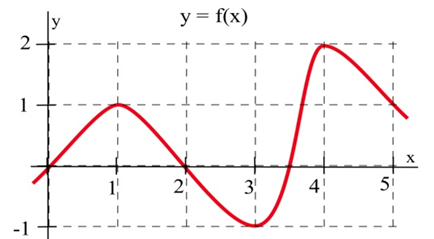
(a) ¿A qué valores de\(x\) la gráfica de\(f\) en la gráfica tiene una línea tangente horizontal?
b) ¿A qué valor (s) de\(x\) es el valor\(f\) del mayor? ¿más pequeña?
(c) Esbozar la gráfica de\(m(x)\) = la pendiente de la línea tangente a la gráfica de\(f\) en el punto\((x,y)\)
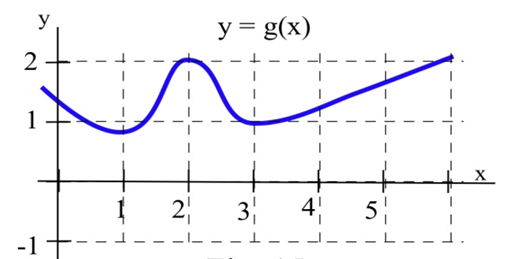
a) ¿A qué valores de\(x\) la gráfica de\(g\) tiene una línea tangente horizontal?
b) ¿A qué valor (s) de\(x\) es el valor\(g\) del mayor? ¿más pequeña?
(c) Esbozar la gráfica de\(m(x) =\) la pendiente de la línea tangente a la gráfica de\(g\) en el punto\((x,y)\).
Haga coincidir las descripciones de la situación con el gráfico de tiempo-velocidad correspondiente.
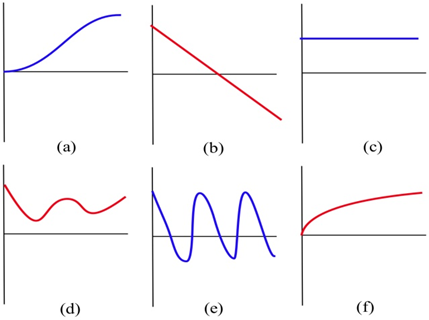
a) Un automóvil que sale rápidamente de una señal de alto.
b) Un automóvil que sale sedatamente de una señal de alto.
c) Un estudiante que rebota en una cama elástica.
d) Una pelota arrojada hacia arriba.
(e) Un estudiante que camina con confianza por el campus para tomar una prueba de cálculo.
(f) Un estudiante no preparado caminando por el campus para tomar una prueba de cálculo.
Para cada función\(f(x)\) en los problemas 14 — 19, realice los pasos (a) — (d):
a) calcular\(m_{\sec} = \frac{f(x+h)-f(x)}{h}\) y simplificar
b) determinar\(m_{\tan} = \lim_{h \to 0} m_{\sec}\)
c) evaluar\(m_{\tan} \) en\(x = 2\),
(d) encontrar la ecuación de la línea tangente a la gráfica de\(f\)\((2, f(2) )\)
| 14. \(f(x) = 3x – 7\) | 15. \(f(x) = 2 – 7x\) | 16. \(f(x) = ax + b\)donde\(a\) y\(b\) son constantes |
| 17. \(f(x) = x^2 + 3x\) | 18. \(f(x) = 8 – 3x^2\) | 19. \(f(x) = ax^2 + bx + c\)donde\(a\),\(b\) y\(c\) son constantes |
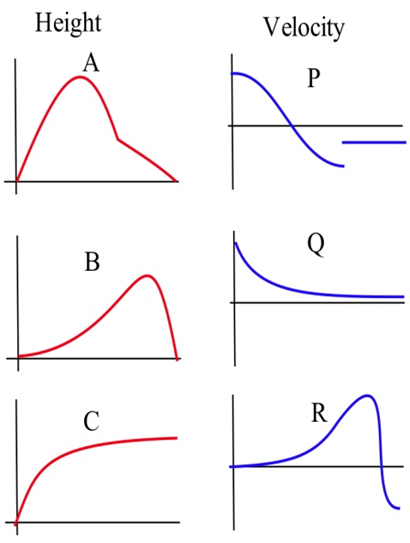
Coincidir las gráficas de las tres funciones siguientes con las gráficas de sus derivadas.
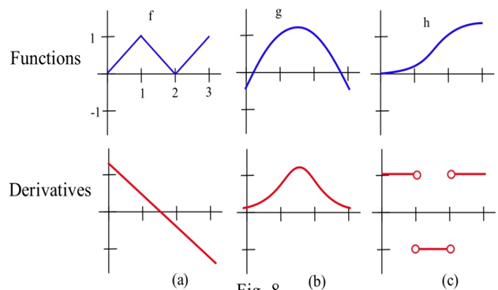
A continuación se presentan seis gráficas, tres de las cuales son derivadas de las otras tres. Emparejar las funciones con sus derivadas.
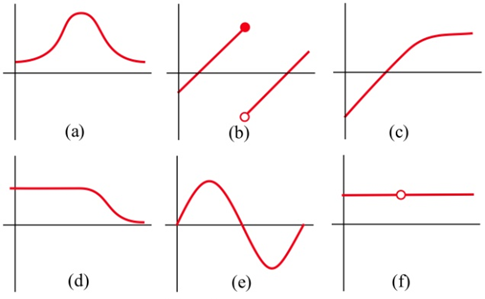
La gráfica a continuación muestra la temperatura durante un día de verano en Chicago. Esboce la gráfica de la velocidad a la que cambia la temperatura. (Esta es solo la gráfica de las pendientes de las líneas que son tangentes a la gráfica de temperatura).
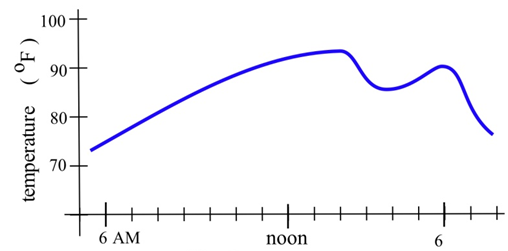
Rellene la mesa con las unidades correspondientes para\(f '(x)\).
|
unidades para\(x\) |
unidades para\(f(x)\) |
unidades para\(f '(x)\) |
|
horas |
millas |
|
|
personas |
automóviles |
|
|
dólares |
panqueques |
|
|
días |
trucha |
|
|
segundos |
millas por segundo |
|
|
segundos |
galones |
|
|
horas de estudio |
puntos de prueba |
Si\(C(x)\) es el costo total, en millones, de producir\(x\) mil artículos, interprete\(C'(4) = 2\).
Supongamos que\(P(t)\) es el número de individuos infectados por una enfermedad\(t\) días después de que se detectó por primera vez. Interpretar\(P'(50) = -200\).
2.3 Ejercicios
Rellene los valores en la tabla para\(\frac{d}{dx} (3(f(x))\),\(\frac{d}{dx}(2f(x)+g(x))\), y\(\frac{d}{dx}(3(g(x)-f(x))\).
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (3(f(x))\) | \(\frac{d}{dx}(2f(x)+g(x))\) | \(\frac{d}{dx}(3(g(x)-f(x))\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
Encuentra
(a)\(D( x^{12} )\)
b)\(\frac{d}{dx} (\sqrt[7]{x})\)
c)\(D(\frac{1}{x^3})\)
d)\(\frac{d x^e}{dx}\)
Encuentra
(a)\(D( x^{9} )\)
b)\(\frac{d x^{2/3}}{dx}\)
c)\(D(\frac{1}{x^4})\)
d)\(D(x^{\pi})\)
En los problemas 4 — 8, a) calcular\(f '(1)\) y b) determinar cuándo\(f '(x) = 0\).
| 4. \(f(x) = x^2 – 5x + 13\) |
| 5. \(f(x) = 5x^2 – 40x + 73\) |
| 6. \(f(x) = x^3 + 9x^2 + 6\) |
| 7. \(f(x) = x^3 + 3x^2 + 3x – 1\) |
| 8. \(f(x) = x^3 + 2x^2 + 2x – 1\) |
¿Dónde\(g(x) = x^3 – 12x\) tienen\(f(x) = x^2 – 10x + 3\) y tienen líneas tangentes horizontales?
Se necesitan\(T(x) = x^2\) horas para tejer alfombras\(x\) pequeñas. ¿Cuál es el tiempo marginal de producción para tejer una alfombra? (Asegúrese de incluir las unidades con su respuesta.)
Cuesta\(C(x) = \sqrt{x}\) dólares producir x pelotas de golf. ¿Cuál es el costo marginal de producción para hacer una pelota de golf? ¿Cuál es el costo marginal de producción cuando\(x = 25\)? ¿Cuándo\(x= 100\)? (Incluir unidades.)
Una flecha disparada hacia arriba desde el nivel del suelo con una velocidad inicial de 128 pies por segundo estará a\(h(x) = –16x^2 + 128x\) pies de altura en\(x\) segundos.
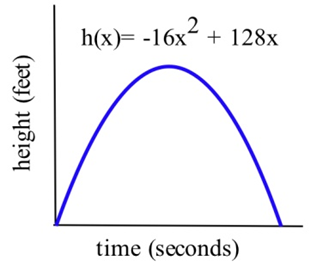
(a) Determinar la velocidad de la flecha cuando\(x =\) 0, 1 y 2 segundos.
b) ¿Cuál es la velocidad de la flecha\(v(x)\), en cualquier momento\(x\)?
(c) ¿A qué hora\(x\) será 0 la velocidad de la flecha?
d) ¿Cuál es la mayor altura que alcanza la flecha?
e) ¿Cuánto tiempo estará la flecha en alto?
(f) Utilizar la respuesta para la velocidad en la parte (b) para determinar la aceleración,\(a(x) = v '(x)\), en cualquier momento\(x\).
Si una flecha es disparada hacia arriba desde el nivel del suelo en la luna con una velocidad inicial de 128 pies por segundo, su altura será\(h(x) = –2.65x^2 + 128x\) pies en\(x\) segundos. Hacer las partes (a) — (e) del problema 40 usando esta nueva ecuación para\(h\).
\(f(x) = x^3 + A x^2 + B x + C\)con constantes\(A\),\(B\) y\(C\). ¿Se pueden encontrar condiciones sobre las constantes\(A\),\(B\) y\(C\) cuáles garantizarán que la gráfica de\(y = f(x)\) tenga dos “vértices” distintos? (Aquí un “vértice” significa un lugar donde la curva cambia de aumentar a disminuir o de disminuir a aumentar).
2.4 Ejercicios
Usa los valores de la tabla para rellenar el resto de la tabla.
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (f(x) \cdot g(x))\) | \(\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right)\) | \(\frac{d}{dx}\left(\frac{g(x)}{f(x)}\right)\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
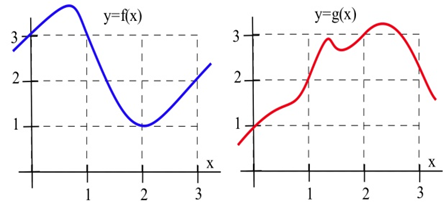
2. Utilice la información de la gráfica para trazar los valores de las funciones\(f + g\),\(f \cdot g\)\(f/g\) y sus derivadas en\(x =\) 1, 2 y 3.
3. Utilice la información de la gráfica para trazar los valores de las funciones\(2f\),\(f – g\)\(g/f\) y sus derivadas en\(x =\) 1, 2 y 3.
Calcular\(\frac{d}{dx} ((x-5)(3x+7))\) por (a) usando la regla del producto y (b) expandiendo el producto y luego diferenciando. Verificar que ambos métodos den el mismo resultado.
Si el producto de\(f\) y\(g\) es una constante\(( f(x) \cdot g(x) = k\) para todos\(x\)), entonces ¿cómo están\(\frac{\frac{d}{dx}(f(x))}{f(x)}\) y\(\frac{\frac{d}{dx}(g(x))}{g(x)}\) relacionados?
Si el cociente de\(f\) y\(g\) es una constante (\(\frac{f(x)}{g(x)} = k\)para todos\(x\)), entonces ¿cómo están\(g \cdot f'\) y\(f \cdot g '\) relacionados?
En los problemas 7 a 8, a) calcular\(f '(1)\) y b) determinar cuándo\(f '(x) = 0\)
| 7. \(f(x) = \frac{7x}{x^2+4}\) | 8. \(f(x) = \frac{3x^2}{2x-3}\) |
Determinar\(\frac{d}{dx}(x^2 + 1)(7x - 3)\) y\(\frac{d}{dt}(\frac{3t-2}{5t+1})\).
Hallar (a)\(\frac{d}{dx}(x^3e^x)\) y (b)\(\frac{d}{dx}(e^x)^3\).
Buscar (a)\(\frac{d}{dt} (te^t)\), (b)\(d(e^x)^5\)
Un fabricante ha determinado que un empleado con d días de experiencia en producción podrá producir aproximadamente\(P(d) = 3 + 15( 1 – e^{–0.2d} )\) artículos por día. Gráfica\(P(d)\).
(a) Aproximadamente, ¿cuántos artículos podrá producir un empleado principiante cada día?
b) ¿Cuántos artículos podrá producir un empleado experimentado cada día?
c) ¿Cuál es la tasa marginal de producción de un empleado con 5 días de experiencia? (¿Cuáles son las unidades de tu respuesta y qué significa esta respuesta?
2.5 Ejercicios
Se muestra la\(y = f(x)\) gráfica de.
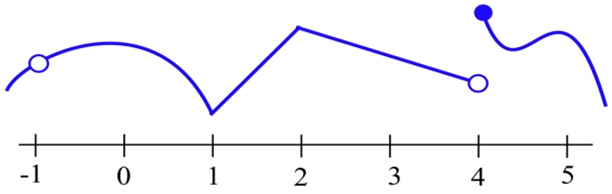
a) ¿En qué enteros es\(f\) continuo?
b) ¿En qué enteros es\(f\) diferenciable?
Se muestra la\(y = g(x)\) gráfica de.
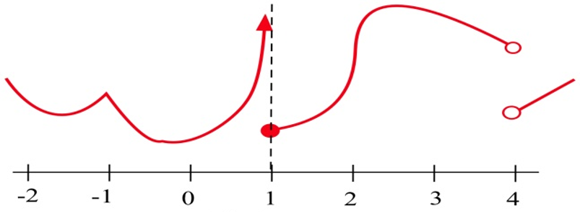
a) ¿En qué enteros es\(g\) continuo?
b) ¿En qué enteros es\(g\) diferenciable?
Los problemas 3 y 4 se refieren a los valores dados en esta tabla:
| \(x\) | \(f(x)\) | \(g(x)\) | \(f'(x)\) | \(g'(x)\) | \((f \circ g)(x)\) | \((f \circ g)' (x)\) |
| -2 | 2 | -1 | 1 | 1 | ||
| -1 | 1 | 2 | 0 | 2 | ||
| 0 | -2 | 1 | 2 | -1 | ||
| 1 | 0 | -2 | -1 | 2 | ||
| 2 | 1 | 0 | 1 | -1 |
3. Utilice la tabla de valores para determinar\(( f \circ g )(x)\) y\(( f \circ g )' (x)\) en\(x =\) 1 y 2.
4. Utilice la tabla de valores para determinar\(( f \circ g )(x)\) y\(( f \circ g )' (x)\) en\(x =\) —2, —1 y 0.
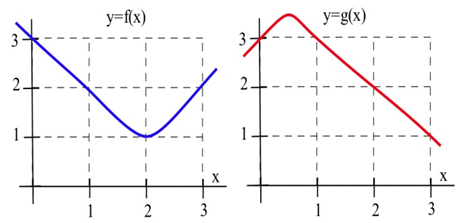
5. Utilice las gráficas para estimar los valores de\(g(x)\),\(\bf g '(x)\),\((f \circ g)(x)\),\(\mathbf{f '(} g(x) \mathbf{)}\), y\(\mathbf{( f \circ g ) '(} x \mathbf{)}\) at\(x = 1\).
6. Utilice las gráficas para estimar los valores de\(g(x)\)\(\bf g '(x)\),\((f \circ g)(x)\),\(\mathbf{f '(} g(x) \mathbf{)}\), y\(\mathbf{( f \circ g ) '(} x \mathbf{)}\) para\(x = 2\).
En los problemas 7 — 12, encuentra la derivada de cada función.
| 7. \(f(x) = (2x – 8)^5\) | 8. \(f(x) = (6x – x^2)^{10}\) | 9. \(f(x) = x \cdot (3x + 7)^5\) |
| 10. \(f(x) = (2x + 3)^6 \cdot (x – 2)^4\) | 11. \(f(x) = \sqrt{x^2 + 6x - 1}\) | 12. \(f(x) = \frac{x-5}{(x+3)^4}\) |
Si\(f\) es una función diferenciable,
(a) ¿cómo son las gráficas de\(y = f(x)\) y\(y = f(x) + k\) relacionadas?
b) ¿Cómo son los derivados\(f(x)\) y\(f(x) + k\) relacionados?
2.6 Ejercicios
En los problemas 1 y 2, cada cita es una declaración sobre una cantidad de algo que cambia con el tiempo. Dejar\(f(t)\) representar la cantidad a tiempo\(t\). Para cada cotización, diga qué\(f\) representa y si la primera y segunda derivadas de\(f\) son positivas o negativas.
1. a) “El desempleo volvió a subir, pero la tasa de incremento es menor que el mes pasado”.
(b) “Nuestras ganancias volvieron a disminuir, pero a un ritmo más lento que el mes pasado”.
c) “La población sigue en alza y a un ritmo más rápido que el año pasado”.
2. a) “La temperatura del niño sigue subiendo, pero más lenta de lo que era hace unas horas”.
b) “El número de ballenas está disminuyendo, pero a un ritmo más lento que el año pasado”.
c) “El número de personas con gripe va en aumento y a un ritmo más rápido que el mes pasado”.
¿En qué intervalos está la función en la gráfica (a) cóncava hacia arriba? b) ¿cóncavo hacia abajo?
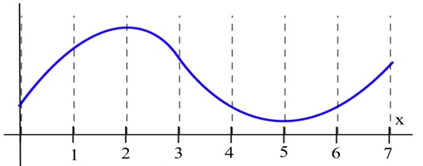
¿En qué intervalos es cóncava hacia arriba la función en la gráfica (a)? b) ¿cóncavo hacia abajo?
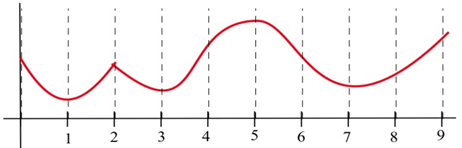
Esbozar las gráficas de funciones definidas y cóncavas en todas partes y que tienen
(a) sin raíces.
b) exactamente 1 raíz.
c) exactamente 2 raíces.
d) exactamente 3 raíces.
En los problemas 6 — 9, una función y valores de\(x\) así que\(f '(x) = 0\) se dan. Utilice la Prueba de Segunda Derivada para determinar si cada punto\((x, f(x))\) es un máximo local, un mínimo local o ninguno
| 6. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 7. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3 \). |
| 8. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
| 9. \(f(x) = x \cdot \ln(x), x = 1/e \). |
¿Cuáles de los puntos etiquetados en la gráfica son puntos de inflexión?
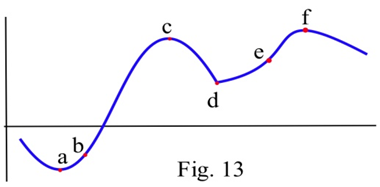
¿Cuáles de los puntos etiquetados en la gráfica son puntos de inflexión?
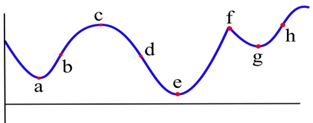
¿Cuántos puntos de inflexión puede
(a) polinomio cuadrático tener?
(b) polinomio cúbico tienen?
c) polinomio de grado\(n\) tener?
Rellene la tabla con “+”, “—” o “0" para la función mostrada.
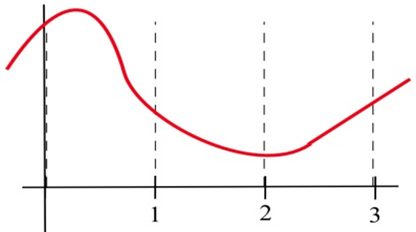
| \(x\) | \(f(x)\) | \(f'(x)\) | \(f''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
Rellene la tabla con “+”, “—” o “0" para la función mostrada.
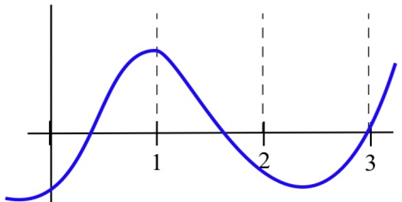
| \(x\) | \(g(x)\) | \(g'(x)\) | \(g''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
En los problemas 15 — 21, encuentra la derivada y la segunda derivada de cada función.
| 15. \(f(x) = 7x^2 + 5x – 3\) |
| 16. \(f(x) = (2x – 8)^5\) |
| 17. \(f(x) = (6x – x^2)^{10}\) |
| 18. \(f(x) = x \cdot (3x + 7)^5 \) |
| 19. \(f(x) = (2x^3 + 3)^6\) |
| 20. \(f(x) = \sqrt{x^2 + 6x - 1}\) |
| 21. \(f(x) = \ln (x^2+4)\) |
2.7 Ejercicios
Encuentre todos los puntos críticos de la función mostrada e identifíquelos como máximo local, mínimo local, o ninguno de ellos. Encuentra el máximo global y el mínimo en el intervalo.
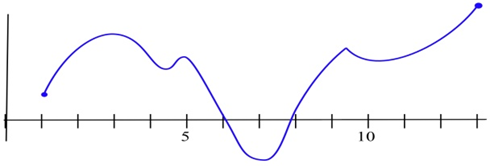
Encuentre todos los puntos críticos de la función mostrada e identifíquelos como máximo local, mínimo local, o ninguno de ellos. Encuentra el máximo global y el mínimo en el intervalo.
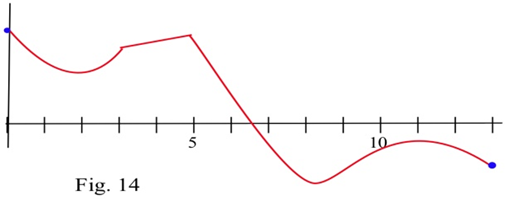
En los problemas 3 — 8, encuentra todos los puntos críticos y máximos y mínimos locales de cada función.
| 3. \(f(x) = x^2 + 8x + 7\) | 4. \(f(x) = 2x^2 – 12x + 7\) |
| 5. \(f(x) = x^3 – 6x^2 + 5\) | 6. \(f(x) = (x – 1)^2 (x – 3)\) |
| 7. \(f(x) = \ln ( x^2 – 6x + 11 )\) | 8. \(f(x) = 2x^3 – 96x + 42\) |
En los problemas 9 — 16, encuentra todos los puntos críticos y extremos globales de cada función en los intervalos dados.
| 9. \(f(x) = x^2 – 6x + 5\)en toda la línea del número real. |
| 10. \(f(x) = 2 – x^3\)en toda la línea del número real. |
| 11. \(f(x) = x^3 – 3x + 5\)en toda la línea del número real. |
| 12. \(f(x) = x - e^x\)en toda la línea del número real. |
| 13. \(f(x) = x^2 – 6x + 5\)el [—2, 5]. |
| 14. \(f(x) = 2 – x^3\)el [—2, 1]. |
| 15. \(f(x) = x^3 – 3x + 5\)el [—2, 1]. |
| 16. \(f(x) = x-e^x\)el [1, 2]. |
Supongamos\(f(1) = 5\) y\(f '(1) = 0\). ¿Qué podemos concluir sobre el punto (1,5) si
a)\(f '(x) < 0\) para\(x < 1\), y\(f '(x) > 0\) para\(x > 1\)?
b)\(f '(x) < 0\) para\(x < 1\), y\(f '(x) < 0\) para\(x > 1\)?
c)\(f '(x) > 0\) para\(x < 1\), y\(f '(x) < 0\) para\(x > 1\)?
d)\(f '(x) > 0\) para\(x < 1\), y\(f '(x) > 0\) para\(x > 1\)?
\(A(x)\)Definir como el área delimitada entre el\(x\) eje —eje, la gráfica de\(f\), y una línea vertical en\(x\).
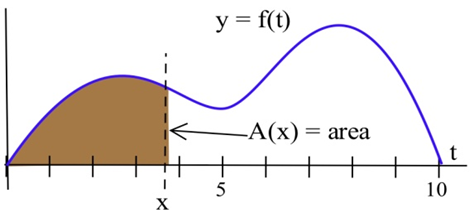
a) ¿A qué valor de\(x\) es\(A(x)\) mínimo?
b) ¿A qué valor de\(x\) es\(A(x)\) máximo?
Definir\(S(x)\) para que sea la pendiente de la línea a través de los puntos\((0,0)\) y con\(( x, f(x) )\) base en la gráfica de que\(f\) se muestra.
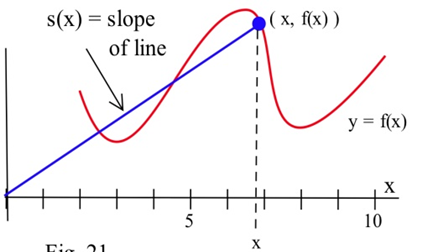
a) ¿A qué valor de\(x\) es\(S(x)\) mínimo?
b) ¿A qué valor de\(x\) es\(S(x)\) máximo?
La gráfica de la derivada de una función continua\(f\).
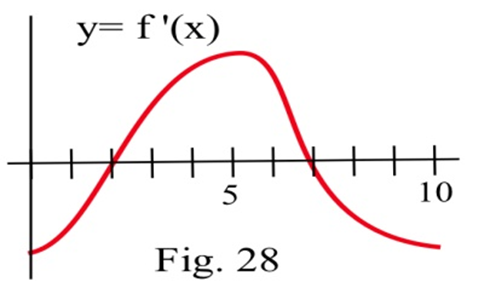
(a) Enumerar los números críticos de\(f\).
b) ¿Para qué valores de\(x\)\(f\) tiene un máximo local?
c) ¿Para qué valores de\(x\)\(f\) tiene un mínimo local?
La gráfica de la derivada de una función continua\(g\).
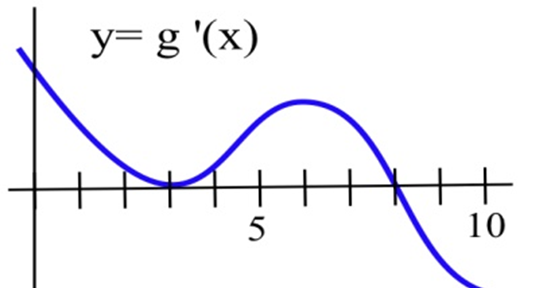
(a) Enumerar los números críticos de\(g\).
b) ¿Para qué valores de\(x\)\(g\) tiene un máximo local?
c) ¿Para qué valores de\(x\)\(g\) tiene un mínimo local?
En los problemas 22 — 24, una función y valores de\(x\) así que\(f '(x) = 0\) se dan. Utilice la Prueba de Segunda Derivada para determinar si cada punto\((x, f(x))\) es un máximo local, un mínimo local o ninguno
| 22. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 23. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3\). |
| 24. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
2.8 Ejercicios
Esbozar la gráfica de una función continua\(f\) para que
a)\(f(1) = 3\),\(f '(1) = 0 \), y el punto (1,3) es un máximo local de\(f\).
b)\(f(2) = 1\),\(f '(2) = 0 \), y el punto 2.1 es un mínimo local de\(f\).
(c)\(f(5) = 4\),\(f '(5) = 0\), y el punto (5,4) no es un mínimo o máximo local de\(f\).
En los problemas 2—4, esboce la gráfica de la derivada de cada función.
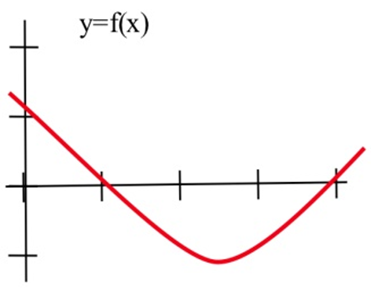
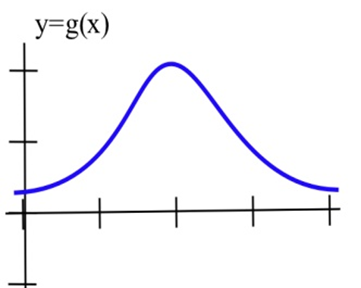
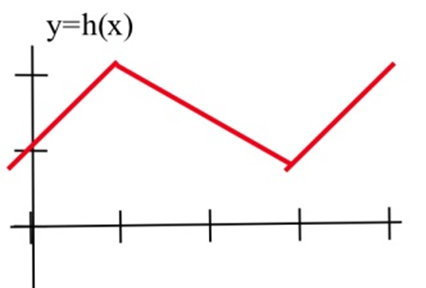
En los problemas 5—7, se muestra la gráfica de la altura de un helicóptero. Esboce el gráfico de la velocidad ascendente del helicóptero.
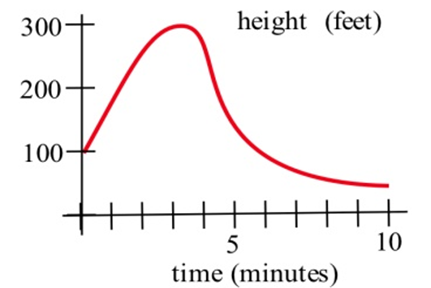
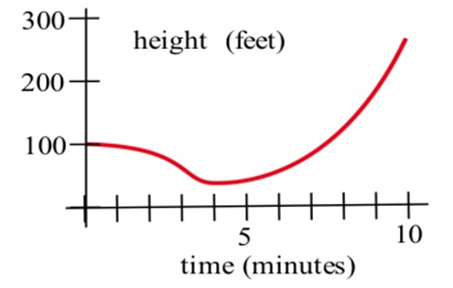
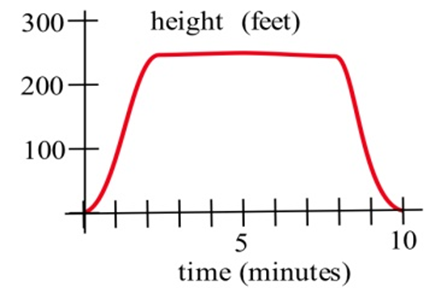
En las gráficas de la derecha, coinciden las gráficas de las funciones con las de sus derivadas
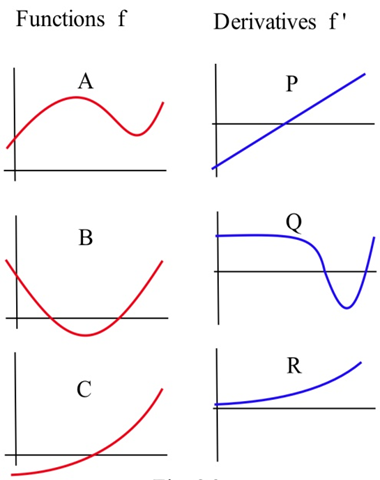
En las gráficas que aparecen a continuación, coinciden las gráficas que muestran las alturas de los cohetes con las que muestran sus velocidades.
En los problemas 10 — 14, utilice la información de las derivadas de cada función para ayudarle a graficar la función. Encuentra todos los máximos y mínimos locales de cada función.
| 10. \(f(x) = x^3 – 3x^2 – 9x – 5\) | 11. \(g(x) = 2x^3 – 15x^2 + 6\) | 12. \(h(x) = x^4 – 8x^2 + 3\) |
| 13. \(r(t) = \frac{2}{t^2+1}\) | 14. \(f(x) = \frac{x^2+3}{x}\) |
2.9 Ejercicios
(a) Tiene 200 pies de cercado disponibles para construir una pluma rectangular con un divisor de cerco en la mitad (ver abajo). ¿Qué dimensiones de la pluma encierran el área total más grande?
(b) Si necesita 2 divisores, ¿qué dimensiones de la pluma encierran el área más grande?
c) ¿Cuáles son las dimensiones en las partes (a) y (b) si un borde del corral bordea un río y no requiere ningún cercado?

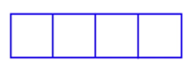
Tienes 120 pies de esgrima para construir una pluma con 4 puestos de igual tamaño. Si la pluma es rectangular y tiene forma como la de abajo, ¿cuáles son las dimensiones de la pluma de mayor área y cuál es esa área?
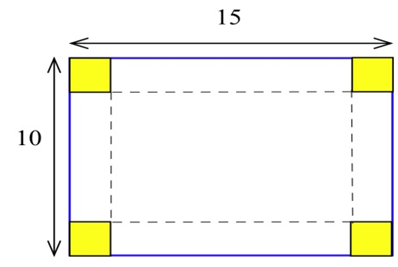
Supongamos que decide cercar el jardín rectangular en la esquina de su patio. Entonces dos lados del jardín están delimitados por la cerca del patio que ya está ahí, por lo que solo necesitas usar los 80 pies de esgrima para encerrar los otros dos lados. ¿Cuáles son las dimensiones del nuevo jardín de mayor superficie? ¿Cuáles son las dimensiones del jardín rectangular de mayor área en la esquina del patio si tienes\(F\) pies de cercado nuevo disponibles?
(a) Tienes una pieza de lata de 10 pulgadas por 15 pulgadas que planeas formar en una caja (sin tapa) cortando un cuadrado de cada esquina y doblando los lados. ¿Cuánto debes cortar de cada esquina para que la caja resultante tenga el mayor volumen?
(b) Si la pieza de hojalata es\(A\)\(B\) pulgadas por pulgadas, ¿cuánto debes cortar de cada esquina para que la caja resultante tenga el mayor volumen?
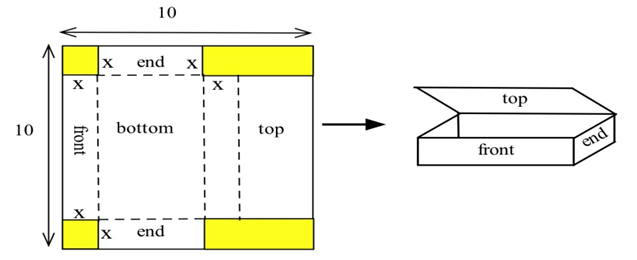
Tienes un pedazo de cartón de 10 pulgadas por 10 pulgadas que planeas cortar y doblar como se muestra para formar una caja con una parte superior. Encuentra las dimensiones de la caja que tiene el mayor volumen.
(a) Se le ha pedido que puje por la construcción de una caja de fondo cuadrado sin tapa que contendrá 100 pulgadas cúbicas de agua. Si el fondo y los lados están hechos del mismo material, ¿cuáles son las dimensiones de la caja que menos material utiliza? (Supongamos que no se desperdicia material).
(b) Supongamos que la caja en la parte (a) utiliza diferentes materiales para el fondo y los lados. Si el material inferior cuesta 5¢ por pulgada cuadrada y el material lateral cuesta 3¢ por pulgada cuadrada, ¿cuáles son las dimensiones de la caja menos costosa que contendrá 100 pulgadas cúbicas de agua?
(a) Determinar las dimensiones de la lata cilíndrica menos costosa que contendrá 100 pulgadas cúbicas si los materiales cuestan 2¢, 5¢ y 3¢ respectivamente para la parte superior, inferior y lados.
(b) ¿Cómo pueden cambiar las dimensiones de los menos costosos si el material inferior cuesta más de 5¢ por pulgada cuadrada?
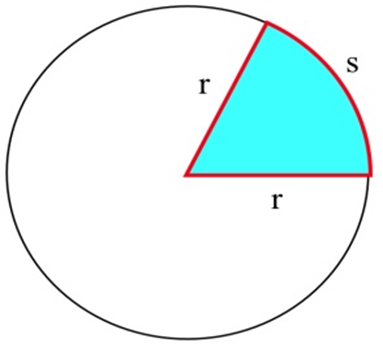
Tienes 100 pies de esgrima para construir una pluma en forma de sector circular, la “rebanada de pastel” que se muestra. El área de tal sector es\((rs)/2\). ¿Qué valor de\(r\) maximiza el área cerrada?
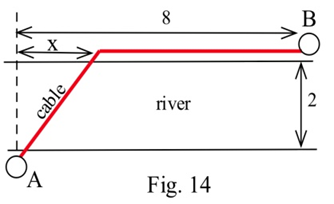
(a) Se le ha pedido determinar la ruta menos costosa para un cable telefónico que conecta Andersonville con Beantown. Si cuesta $5000 por milla tender el cable en tierra y $8000 por milla tender el cable a través del río y el costo del cable es insignificante, encuentre la ruta menos costosa.
b) Cuál es la ruta menos costosa si el cable cuesta $7000 por milla más el costo de tenderlo.
Se le ha pedido determinar dónde se debe construir una obra de agua a lo largo de un río entre Chesterville y Denton para minimizar el costo total de la tubería a los pueblos.
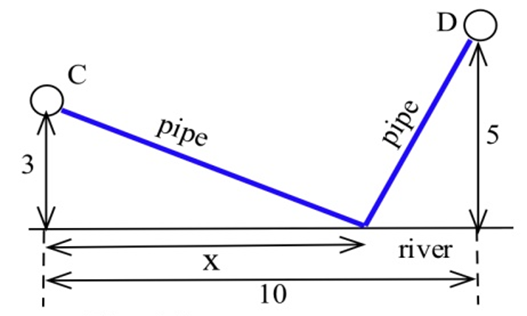
a) Supongamos que se usa el mismo tamaño (y costo) de tubería para cada pueblo. (Esta parte se puede hacer rápidamente sin usar cálculo).
b) Supongamos que la tubería a Chesterville cuesta $3000 por milla y a Denton cuesta $7000 por milla.
Las regulaciones postales de Estados Unidos establecen que la suma de la longitud y circunferencia (distancia alrededor) de un paquete no debe ser superior a 108 pulgadas.
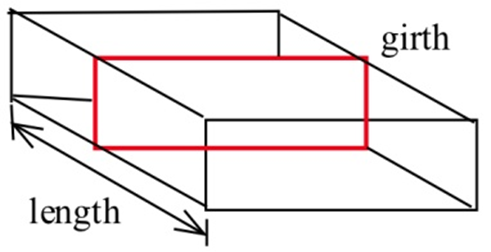
(a) Encontrar las dimensiones de la caja aceptable con un extremo cuadrado que tenga el mayor volumen.
(b) Encontrar las dimensiones de la caja aceptable que tenga el mayor volumen si su extremo es un rectángulo dos veces más largo que ancho.
(c) Encontrar las dimensiones de la caja aceptable con un extremo circular que tenga el mayor volumen.
D. Simonton afirma que los “niveles de productividad” de las personas en diferentes campos pueden describirse como una función de su “edad de carrera”\(t\) por\(p(t) = e^{–at} – e^{ –bt}\) donde\(a\) y\(b\) son constantes que dependen del campo de trabajo, y la edad de carrera es aproximadamente 20 menos que la edad real del individual.
a) A partir de este modelo, ¿a qué edades\((a=.02, b=.03)\) alcanzan matemáticos\((a=.03, b=.05)\)\((a=.02, b=.04)\), geólogos e historiadores su máxima productividad?
(b) Simonton dice “Con un poco de cálculo podemos demostrar que la curva\(( p(t) )\) maximiza en\(t = \frac{1}{b-a} \ln(\frac{b}{a})\).” Usa el cálculo para demostrar que Simonton es correcto.
Nota: Los modelos de este tipo tienen usos para describir el comportamiento de los grupos, pero es peligroso y generalmente no válido aplicar descripciones de grupo o comparaciones a individuos del grupo.
(Genio científico, por Dean Simonton, Cambridge University Press, 1988, pp. 69 — 73)
Tienes un pequeño avión que tiene capacidad para un máximo de 20 pasajeros. Te cuesta $100 por vuelo de Santo Tomás a Santa Croix por gasolina y salarios más un adicional de $6 por pasajero por el gas extra requerido por el peso extra. El cargo por pasajero es de $30 cada uno si 10 personas charter tu avión (10 es el número mínimo que volarás), y este cargo se reduce en $1 por pasajero por cada pasajero mayor de 10 que va (es decir, si van 11 van cada uno pagan $29, si van 12 pagan cada uno $28, etc.). ¿Qué número de pasajeros en un vuelo maximizará sus ganancias?
En la planeación de una cafetería, estimamos que si hay asientos para entre 40 y 80 personas, la ganancia diaria será de $50 por asiento. Sin embargo, si la capacidad de asientos es de más de 80 plazas, la ganancia diaria por asiento se reducirá en $1 por cada asiento adicional de más de 80. ¿Cuál debería ser la capacidad de asientos para maximizar el beneficio total de la cafetería?
En la planeación de un restaurante de tacos, estimamos que si hay asientos para entre 10 y 40 personas, la ganancia diaria será de $10 por asiento. Sin embargo, si la capacidad de asientos es de más de 40 plazas, la ganancia diaria por asiento se reducirá en $0.20 por asiento. ¿Cuál debería ser la capacidad de asientos para maximizar el beneficio total del restaurante de tacos?
El costo total en dólares para que Alicia haga manoplas de\(q\) horno viene dado por\(C(q) = 64+1.5q+.01q^2\).
a) ¿Cuál es el costo fijo?
(b) Encontrar una función que dé el costo marginal.
(c) Encontrar una función que dé el costo promedio.
d) Encontrar la cantidad que minimice el costo promedio.
(e) Confirmar que el costo promedio y el costo marginal son iguales a su respuesta a la parte (d).
Shaki fabrica y vende colgazos de mochila. El costo total en dólares para que Shaki haga\(q\) colgantes viene dado por\(C(q) = 75+2q+.015q^2\). Encuentra la cantidad que minimiza el costo promedio de Shaki para hacer colgantes.
2.10 Ejercicios
Si\(g(20) = 35\) y\(g'(20)=-2\), estimar el valor de\(g(22)\).
Si\(g(1)=-17\) y\(g'(1)=5\), estimar el valor de\(g(1.2)\).
Utilice la Aproximación de Línea Tangente para estimar la raíz cúbica de 9.
Utilice la Aproximación de Línea Tangente para estimar la quinta raíz de 30.
Un rectángulo tiene un lado en el\(x\) eje —, un lado en el\(y\) eje —y una esquina en la gráfica de\(y = x^2 + 1\).
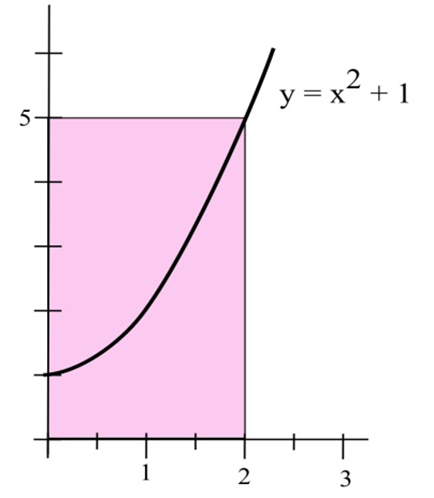
(a) Utilice la fórmula Aproximación lineal del área para estimar el aumento en el área del rectángulo si la base crece de 2 a 2.3 pulgadas.
(b) Calcular exactamente el incremento en el área del rectángulo a medida que la base crece de 2 a 2.3 pulgadas.
Se puede medir el diámetro de un círculo hasta dentro de 0.3 cm.
a) ¿Qué tan grande es el “error” en el área calculada de un círculo con un diámetro medido de 7.4 cm?
b) ¿Qué tan grande es el “error” en el área calculada de un círculo con un diámetro medido de 13.6 cm?
c) ¿Qué tan grande es el error porcentual en el área calculada de un círculo con un diámetro medido de\(d\)?
La función de demanda de las manoplas de horno de Alicia viene dada por\(q=-8p+80\) (\(q\)es el número de manoplas de horno,\(p\) es el precio en dólares). Encuentra la elasticidad de la demanda cuando\(p =\) $7.50. ¿Aumentarán los ingresos si Alicia sube su precio desde $7.50?
La función de demanda para los colgantes de Shaki viene dada por\(q=-35p+205\) (\(q\)es el número de danglies,\(p\) es el precio en dólares por dangly). Encuentra la elasticidad de la demanda cuando\(p =\) $5. ¿Debería Shaki subir o bajar su precio para aumentar los ingresos?
2.11 Ejercicios
En los problemas 1 — 10 encontrar\(dy/dx\) diferenciando implícitamente luego encontrar el valor de\(dy/dx\) en el punto dado.
| 1. \(x^2 + y^2 = 100\), punto (6, 8) | 2. \(x^2 + 5y^2 = 45\), punto (5, 2) |
| 3. \(x^2 – 3xy + 7y = 5\), punto (2,1) | 4. \(\sqrt{x} + \sqrt{y} = 5\), punto (4,9) |
| 5. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), punto (0,4) | 6. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), punto (3,0) |
| 7. \(\ln(y) + 3x – 7 = 0\), punto (2,\(e\)) | 8. \(x^2 – y^2 = 16\), punto (5,3) |
| 9. \(x^2 – y^2 = 16\), punto (5, —3) | 10. \(y^2 + 7x^3 – 3x = 8\), punto (1,2) |
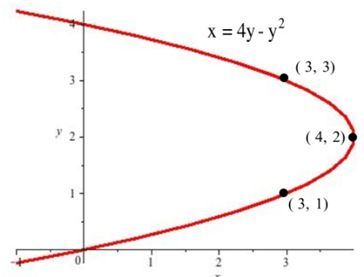
| 11. Encuentra las pendientes de las líneas tangentes a la gráfica en que se muestran en los puntos (3,1), (3,3) y (4,2). |
| 12. Encuentra las pendientes de las líneas tangentes a la gráfica en que se muestra donde la gráfica cruza el\(y\) eje —eje. |
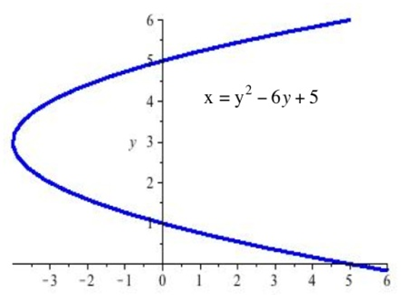
| 13. Encuentra las pendientes de las líneas tangentes a la gráfica en la gráfica que se muestra en los puntos ((5,0), (5,6) y (—4,3). |
| 14. Encuentra las pendientes de las líneas tangentes a la gráfica en la gráfica que se muestra donde la gráfica cruza el\(y\) eje —eje. |
En los problemas 15 — 16, encuentra\(dy/dx\) usando diferenciación implícita y luego encuentra la pendiente de la línea tangente a la gráfica de la ecuación en el punto dado.
| 15. \(y^3 – 5y = 5x^2 + 7\), punto (1,3) | 16. \(y^2 – 5xy + x^2 + 21 = 0\), punto (2,5) |
Una esfera expandible se está llenando de líquido a una velocidad constante desde un grifo (imagínese un globo de agua conectado a un grifo). Cuando el radio de la esfera es de 3 pulgadas, el radio aumenta a 2 pulgadas por minuto. ¿Qué tan rápido sale el líquido del grifo? \(( V = \frac{4}{3} \pi r^3 )\)
La base de 12 pulgadas de un triángulo rectángulo está creciendo a 3 pulgadas por hora, y la altura de 16 pulgadas se está encogiendo a 3 pulgadas por hora.
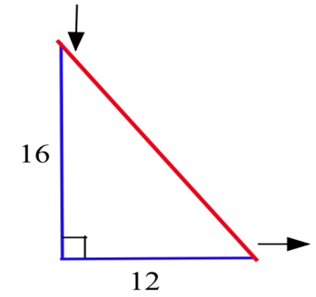
a) ¿Está aumentando o disminuyendo la superficie?
b) ¿El perímetro aumenta o disminuye?
c) ¿La hipotenusa aumenta o disminuye?
Una hora después, el triángulo rectángulo en el Problema 2 mide 15 pulgadas de largo y 13 pulgadas de alto, y la base y la altura están cambiando al mismo ritmo que en el Problema 18.
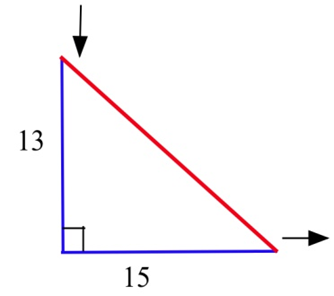
a) ¿La superficie está aumentando o disminuyendo ahora?
b) ¿La hipotenusa aumenta o disminuye ahora?
c) ¿El perímetro aumenta o disminuye ahora?
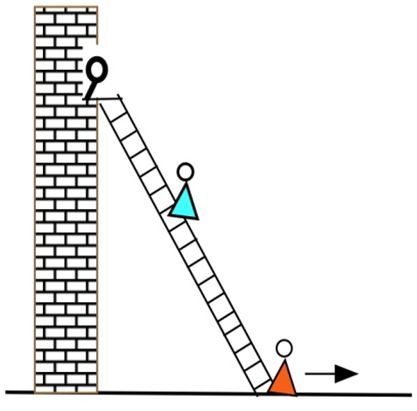
Una joven y su novio planean fugarse, pero ella debe rescatarlo de su madre que lo ha encerrado en su habitación. La joven ha colocado una escalera de 20 pies de largo contra su casa y está golpeando su ventana cuando su madre comienza a tirar del fondo de la escalera lejos de la casa a razón de 3 pies por segundo. ¿Qué tan rápido es la parte superior de la escalera (y la pareja joven) cayendo cuando la parte inferior de la escalera está
(a) ¿a 12 pies del fondo de la pared?
b) ¿A 16 pies del fondo de la pared?
c) ¿a 19 pies del fondo de la pared?
La longitud de un rectángulo de 12 pies por 8 pies está aumentando a una velocidad de 3 pies por segundo y el ancho disminuye a 2 pies por segundo.
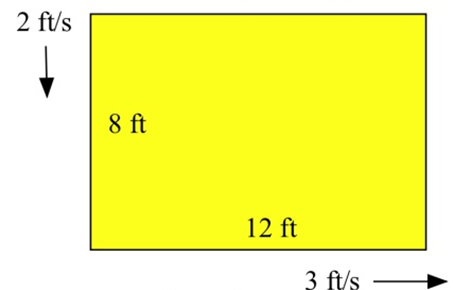
a) ¿Qué tan rápido cambia el perímetro?
b) ¿Qué tan rápido cambia la zona?
Un petrolero en Puget Sound ha surgido una fuga y se está formando una mancha de petróleo circular. La mancha de petróleo tiene 4 pulgadas de grosor en todas partes, mide 100 pies de diámetro y el diámetro aumenta a 12 pies por hora. Tu trabajo, como comandante de la Guardia Costera o capitán del petrolero, es determinar qué tan rápido se escapa el petróleo del petrolero.


