2.11: Otras aplicaciones
- Page ID
- 110573
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aproximación de línea tangente
Cuando pensamos por primera vez en la derivada, usamos la pendiente de líneas secantes a intervalos diminutos para aproximar la derivada:
\[f'(a) \cong \frac{\Delta y}{\Delta x} = \frac{f(x) - f(a)}{x-a} \nonumber\]
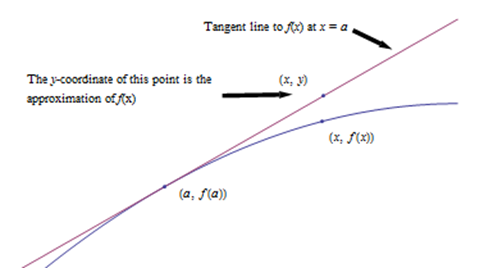
Ahora que tenemos otras formas de encontrar derivados, podemos explotar esta aproximación para ir por el otro lado. Resuelve la expresión anterior para\(f(x)\), y obtendrás la aproximación de la línea tangente:
Para aproximar el valor del\(f(x)\) uso de TLA, encuentra algunos\(a\) donde
- \(a\)y\(x\) están “cerca”, y
- Conoces los valores exactos de ambos\(f (a)\) y\(f ‘(a)\). Entonces\[f(x) \cong f(a) + f'(a)(x-a).\nonumber\]
Otra forma de ver la misma fórmula:
\[\Delta y \cong f'(a) \Delta x\nonumber\]
¿Qué tan cerca está cerca? Depende de la forma de la gráfica de\(f\). En general, cuanto más cerca mejor.
Supongamos que sabemos eso\(g(20) = 5\) y\(g’(20) = 1.4\). Utilice esta información para aproximar\(g(23)\) y\(g(18)\).
Solución
Usando la aproximación de la línea tangente:
\(g(23) \approx 5 + (1.4)(23 – 20) = 9.2\)
\(g(18) \approx 5 + (1.4)(18 – 20) = 2.2\)
Tenga en cuenta que no sabemos si estas aproximaciones están cerca, pero son las mejores que podemos hacer con la información limitada con la que tenemos que empezar. Tenga en cuenta también que 18 y 23 son una especie de cerca de 20, así que podemos esperar que estas aproximaciones sean bastante buenas. Nos sentiríamos más seguros usando esta información para aproximarnos\(g(20.003)\). Nos sentiríamos muy inseguros al usar esta información para aproximarnos\(g(55)\).
Elasticidad
Sabemos que las funciones de demanda están disminuyendo, así que cuando aumenta el precio, la cantidad demandada baja. Pero ¿qué pasa con los ingresos =\( \times \) cantidad de precio? ¿Cuándo los aumentos de precios bajarán los ingresos porque la demanda bajó tanto? ¿O aumentarán los ingresos porque la demanda no bajó mucho?
Supongamos que la función de demanda de una compañía es\(D(p) = 100 - p^2\), y el precio actual de la compañía es de $5. ¿Qué pasará con los ingresos si suben el precio 0.05 dólares?
Solución
Estamos más interesados en cómo se compara el cambio de precio con el cambio de demanda, por lo que vamos a convertir todo a cambios relativos (por ciento).
El precio ha aumentado en\[\frac{\Delta p}{p} = \frac{\$0.05}{\$5} = 0.01 = 1\%\nonumber \]
La demanda disminuyó de\(D(5) = 100-5^2 = 75\) a\(D(5.05) = 100-5.05^2 = 74.4975\), un cambio total de\(75-74.4975 = -0.5025\). Como un cambio relativo, eso es\[\frac{\Delta q}{q} = \frac{-0.05025}{75} = -0.0067 = -0.67\%\nonumber \]
Al subir el precio 1%, la demanda sólo cayó 0.67%. Dado que el precio está aumentando más de lo que cae la demanda, esperaríamos que aumentaran los ingresos totales. En este caso decimos que la demanda es inelástica.
La elasticidad de la demanda es una medida de cómo reacciona la demanda ante los cambios de precios. Está normalizado, eso significa que los precios y cantidades particulares no importan, y todo se trata como un cambio porcentual.
Siguiendo la lógica del ejemplo anterior, queremos comparar el cambio relativo en la demanda con el cambio relativo en el precio, o en otras palabras, queremos mirar\[\frac{\frac{\Delta q}{q}}{\frac{\Delta p}{p}}.\nonumber \] Al aproximar los cambios en la demanda y el precio por los derivados, esta fórmula simplifica a\[\frac{\frac{dq}{q}}{\frac{dp}{p}} = \frac{p}{q}\cdot\frac{dq}{dp}\nonumber \]
Dada una función de demanda que da\(q\) in terms of \(p\), so \(q = D(p)\), the elasticidad de la demanda es\[E=\left|\frac{p}{q}\cdot \frac{dq}{dp}\right| = \left|\frac{p}{q}\cdot D'(p)\right| \nonumber \]
(Tenga en cuenta que dado que la demanda es una función decreciente de\(p\), la derivada es negativa. Por eso tenemos los valores absolutos —así que siempre\(E\) será positivo.)
También puede ver esta fórmula escrita como\[E = - \frac{p \cdot D'(p)}{D(p)}\nonumber \] Las dos formas de la ecuación son equivalentes, y puede usar cualquiera de ellas.
- Si\(E \lt 1\), decimos que la demanda es inelástica. En este caso, al subir los precios se incrementan los ingresos.
- Si\(E \gt 1\), decimos que la demanda es elástica. En este caso, subir los precios disminuye los ingresos.
- Si\(E = 1\), decimos que la demanda es unitaria. \(E = 1\)en puntos críticos de la función de ingresos.
Si el precio aumenta 1%, la demanda disminuirá en E%.
Una empresa vende bobinadoras de\( q \) cinta por año a $\( p \) por bobinadora de cinta. La función de demanda para las bobinadoras de cinta viene dada por\( p=300-0.02q \). Encuentra la elasticidad de la demanda cuando el precio es de $70 cada uno. ¿Un incremento en el precio conducirá a un incremento en los ingresos?
Solución
Primero, tenemos que resolver la ecuación de la demanda para que dé\( q \) en términos de\( p \), para que podamos encontrar\( \frac{dq}{dp} \):\( p=300-0.02q \), así\( q=15000-50p \). Entonces\( \frac{dq}{dp}=-50 \).
Tenemos que encontrar\( q \) cuándo\( p = 70 \):\[ q = 11500. \nonumber \]
Ahora cómpule\[ E=\left| \frac{p}{q}\cdot\frac{dq}{dp} \right|=\left| \frac{70}{11500}\cdot(-50) \right| \approx 0.3 \nonumber \]
\(E \lt 1\), por lo que la demanda es inelástica. Aumentar el precio en 1% solo provocaría una caída de 0.3% en la demanda. Aumentar el precio llevaría a un incremento en los ingresos, por lo que parece que la empresa debería aumentar su precio.
La demanda de productos que la gente tiene que comprar, como las cebollas, tiende a ser inelástica. Aunque el precio suba, la gente todavía tiene que comprar aproximadamente la misma cantidad de cebollas, y los ingresos no bajarán. La demanda de productos sin los que la gente pueda prescindir, o postear la compra, como los autos, tiende a ser elástica. Si el precio sube, la gente simplemente no comprará autos en este momento, y los ingresos bajarán.
Una empresa encuentra la demanda\( q \), en miles, de que sus cometas estén\( q=400-p^2 \) a un precio de\( p \) dólares. Encuentra la elasticidad de la demanda cuando el precio es de $5 y cuando el precio es de $15. Entonces encuentra el precio que maximizará los ingresos.
Solución
Cálculo de la derivada,\( \frac{dq}{dp}=-2p \). La ecuación de elasticidad en función de\( p \) será:\[ E=\left| \frac{p}{q}\cdot\frac{dq}{dp} \right|=\left| \frac{p}{400-p^2}\cdot (-2p) \right| =\left| \frac{-2p^2}{400-p^2} \right| \nonumber \]
Evaluando esto para encontrar la elasticidad en $5 y en $15:
\[ E(5) = \left| \frac{-2(5)^2}{400-(5)^2} \right| \approx 0.133 \nonumber \]Por lo que la demanda es inelástica cuando el precio es de $5.
A un precio de 5 dólares, un incremento de 1% en el precio disminuiría la demanda sólo en 0.133%. Los ingresos podrían aumentarse al aumentar los precios.
\[ E(15) = \left| \frac{-2(15)^2}{400-(15)^2} \right| \approx 2.571 \nonumber \]Por lo que la demanda es elástica cuando el precio es de $15.
A un precio de 15 dólares, un incremento de 1% en el precio disminuiría la demanda en 2.571%. Los ingresos podrían aumentarse al disminuir los precios.
Para maximizar los ingresos, podríamos resolver para cuando\( E = 1 \):\[ \begin{align*} \left| \frac{-2p^2}{400-p^2} \right| & = 1 \\ 2p^2 & = 400-p^2 \\ 3p^2 & = 400 \\ p & = \sqrt{\frac{400}{3}}\approx 11.55. \end{align*} \nonumber \]
Un precio de $11.55 maximizará los ingresos.
Como viste en el último ejemplo, la elasticidad proporciona otra forma de determinar el precio que maximizará los ingresos dada una función de demanda. No es más rápido ni más fácil que los métodos aprendidos anteriormente en el curso, pero eres bienvenido a usar cualquiera de las dos técnicas.


