4.E: Funciones de dos variables (Ejercicios)
- Page ID
- 110552
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)4.1 Ejercicios
\(F(x,y) = x^2-y^2\). Encuentra
a)\(F(0,4)\)
b)\(F(4,0)\)
c)\(F(x,4)\)
d)\(F(4,y)\)
e)\(F(800,800)\)
f)\(F(x,x)\)
g)\(F(x,-x)\)
\(g(s,t)=\sqrt{st^2}\). Encuentra
a)\(g(1,9)\)
b)\(g(9,1)\)
c)\(g(1,t)\)
d)\(g(s,9)\)
e)\(g(w,z+1)\)
Vamos\(f(x,y,z,w) = x^2 - \frac{1}{zw}+xyz^2\). Evaluar\(f(1,2,3,4)\).
Vamos\(f(x,y,z,w) = \sqrt{xy} - w^2 + 102yz\). Evaluar\(f(1,2,3,4)\).
Aquí hay una tabla que muestra la función\(A(t,r)\)
| \(\overset{t}{\downarrow} \ r\rightarrow\) |
.03 |
.04 |
.05 |
.06 |
.07 |
|
1 |
30.45 |
40.81 |
51.27 |
61.84 |
72.51 |
|
2 |
61.84 |
83.29 |
105.17 |
127.50 |
150.27 |
|
3 |
94.17 |
127.50 |
161.83 |
197.22 |
233.68 |
a) Encontrar\(A(2, .05)\)
b) Encontrar\(A(.05, .2)\)
c) ¿Es\(A(t, .06)\) una función creciente o decreciente de\(t \)?
d) ¿Es\(A(3, r)\) una función creciente o decreciente de\(r\)?
Aquí hay una tabla que muestra los valores para la función\(H(t,h)\).
| \(\overset{t}{\downarrow} \ h\rightarrow\) |
100 |
150 |
200 |
|
0 |
100 |
150 |
200 |
|
1 |
110.1 |
160.1 |
210.1 |
|
2 |
110.4 |
160.4 |
210.4 |
|
3 |
100.9 |
150.9 |
200.9 |
|
4 |
81.6 |
131.6 |
181.6 |
|
5 |
52.5 |
102.5 |
152.5 |
a) ¿Es\(H(t, 150)\) una función creciente o decreciente de\(t \)?
b) ¿Es\(H( 4, h)\) una función creciente o decreciente de\(h\)?
c) Rellenar los espacios en blanco: El valor máximo que se muestra en esta tabla es\(H\) (___, ___) =____.
d) Rellenar los espacios en blanco: El valor mínimo que se muestra en esta tabla es\(H\) (___, ___) =____.
En los problemas 7 — 10, trazar los puntos dados.
7. \(A = (0,3,4), B = (1,4,0), C = (1,3,4), D = (1, 4,2)\)
8. \(E = (4,3,0), F = (3,0,1), G = (0,4,1), H = (3,3,1)\)
9. \(P = (2,3,–4), Q = (1,–2,3), R = (4,–1,–2), S = (–2,1,3)\)
10. \(T = (–2,3,–4), U = (2,0,–3), V = (–2,0,0), W = (–3,–1,–2)\)
En los problemas 11 — 14, calcular las distancias entre los puntos dados
11. \(A = (5,3,4), B = (3,4,4)\)
12. \(A = (6,2,1), B = (3,2,1)\)
13. \(A = (3,4,2), B = (–1,6,–2)\)
14. \(A = (–1,5,0), B = (1,3,2)\)
En los problemas 15 — 18, grafica los planos dados.
| 15. \(y = 1\)y\(z = 2\) | 16. \(x = 4\)y\(y = 2\) |
| 17. \(x = 1\)y\(y = 0\) | 18. \(x = 2\)y\(z = 0\) |
En los problemas 19 — 22, se dan el centro y el radio de una esfera. Encuentra una ecuación para la esfera.
| 19. Centro = (4, 3, 5), radio = 3 | 20. Centro = (0, 3, 6), radio = 2 |
| 21. Centro = (5, 1, 0), radio = 5 | 22. Centro = (1, 2, 3), radio = 4 |
En los problemas 23 — 24, se da la ecuación de una esfera. Encuentra el centro y el radio de la esfera.
| 23. \((x–3)^2 + (y+4)^2 + (z–1)^2 = 16\) | 24. \((x+2)^2 + y^2 + (z–4)^2 = 25\) |
Por problemas 25 a 30. Haga coincidir el diagrama de contorno con el dibujo en perspectiva generado por computadora (de la a a a f) que coincide. Explica brevemente tu respuesta.
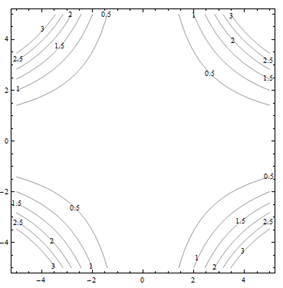
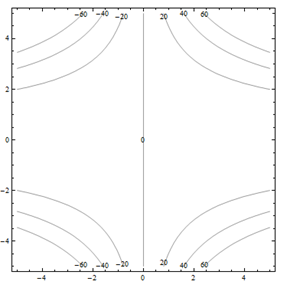
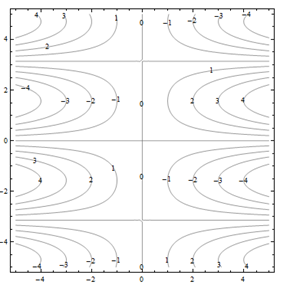
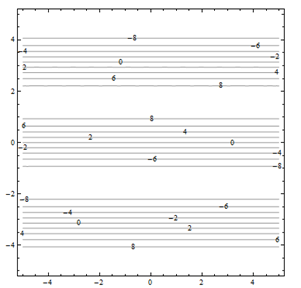
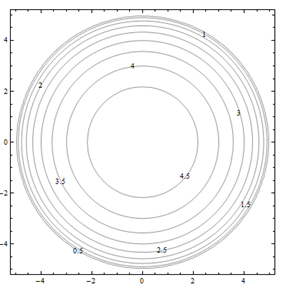
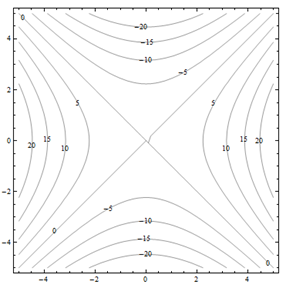
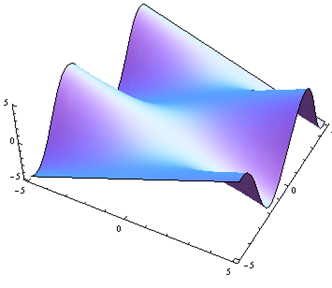
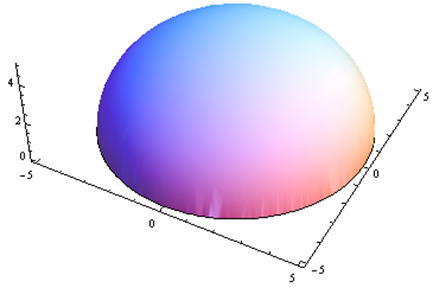
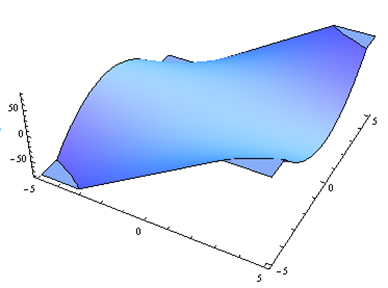
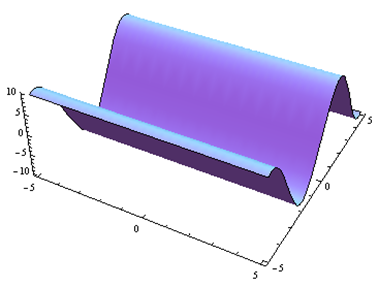
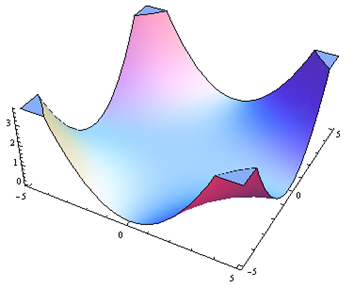
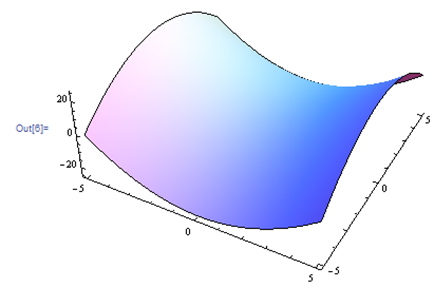
Para problemas 31 a 36. Haga coincidir el diagrama de contorno con la ecuación (de la a a a f) que coincida. Explica brevemente tu respuesta.
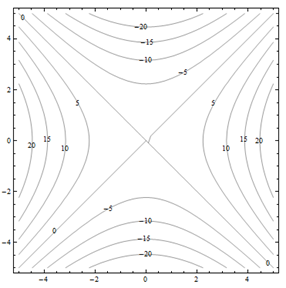
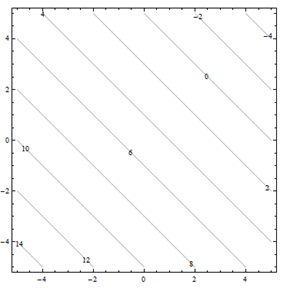
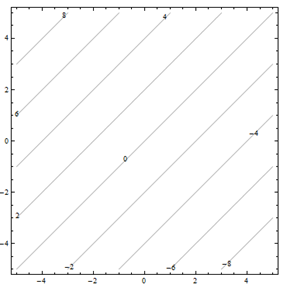
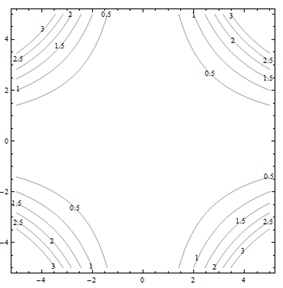
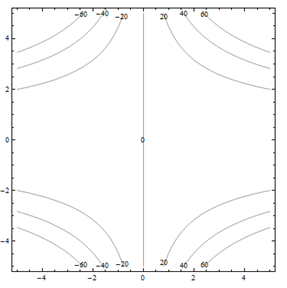
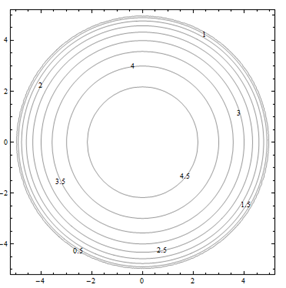
| a.\(f(x,y) = y-x\) | b.\(f(x,y) = xy^2\) |
| c.\(f(x,y) = \sqrt{25-x^2-y^2}\) | d.\(f(x,y) = 5-x-y\) |
| e.\(f(x,y) = 0.01x^2y^2\) | f.\(f(x,y) = x^2-y^2\) |
El diagrama de contorno mostrado es para una función\(M(x, y)\).
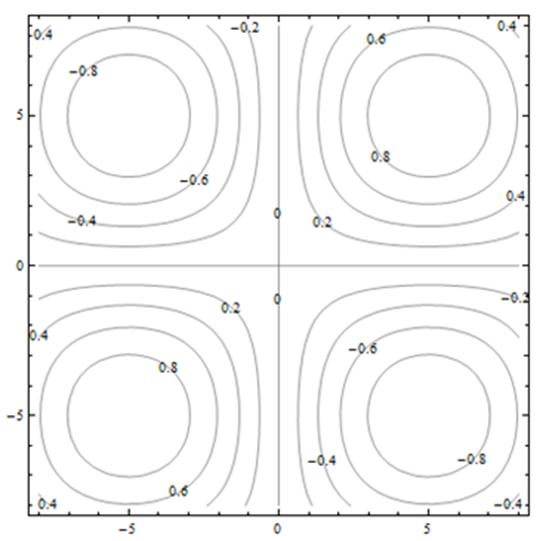
Utilice el diagrama para responder a lo siguiente:
a) Estimación\(M(1, 3)\)
b) Estimación\(M(3, 1)\)
c) ¿Es\(M(x, 3)\) una función creciente o decreciente de\(x\)?
d) ¿Es\(M(3, y)\) una función creciente o decreciente de\(y\)?
e) Encontrar un valor de\(c\) por lo que\(M(c, y)\) es una función constante de\(y\).
El diagrama de contorno mostrado es para una función\(G(x, y)\).
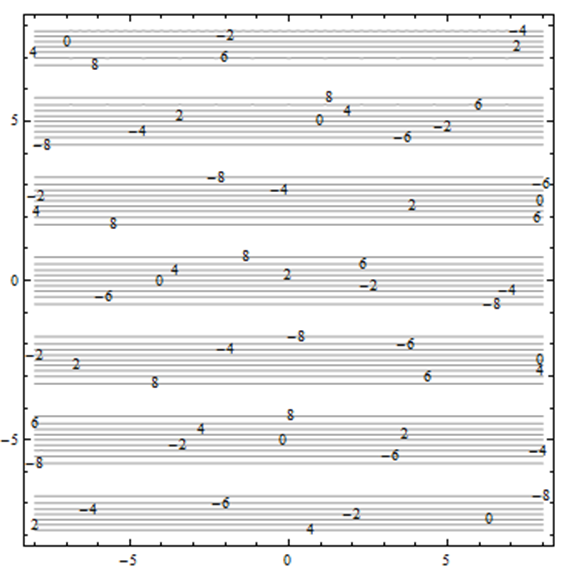
Utilice el diagrama para responder a lo siguiente:
a) Estimación\(G(2, 3)\)
b) Supongamos que viaja hacia el norte (en dirección de incremento\(y\)) a lo largo de la superficie, comenzando por arriba (2, 3). Describe tu viaje.
c) Supongamos que viaja hacia el este (en dirección de incremento\(x\)) a lo largo de la superficie, comenzando por arriba (2, 3). Describe tu viaje.
A continuación se detallan las funciones de demanda para dos productos. \(p_1\),\(p_2\)\(q_1\), y\(q_2\) son los precios (en dólares) y cantidades de los productos 1 y 2. ¿Son estos dos productos productos productos complementarios o bienes sustitutivos?
\[q_1 = 200 -3p_1 + p_2 \nonumber\]
\[q_2 = 150 + p_1 -2p_2 \nonumber\]
A continuación se detallan las funciones de demanda para dos productos. \(p_1\),\(p_2\)\(q_1\), y\(q_2\) son los precios (en dólares) y cantidades de los productos 1 y 2. ¿Son estos dos productos productos productos complementarios o bienes sustitutivos?
\[q_1 = 350 + p_1 + 2p_2 \nonumber\]
\[q_2 = 225 + p_1 + p_2 \nonumber\]
Considere la función Cobb-Douglas Production:\(P(L,K) = 11 L^{0.3} K^{0.7}\). Encuentra el total de unidades de producción cuando se invierten 19 unidades de mano de obra y 12 unidades de capital.
Considere la función Cobb-Douglas Production:\(P(L,K) = 6 L^{0.6} K^{0.4}\). Encuentra el total de unidades de producción cuando se invierten 24 unidades de mano de obra y 8 unidades de capital.
4.2 Ejercicios
Para los problemas del 1 al 16, encontrar\(f_x\) y\(f_y\) para la función dada
| 1. \(f(x,y) = x^2-5y^2\) |
| 2. \(f(x,y) = \frac{x^2-5y^2}{x+4}\) |
| 3. \(f(x,y) = e^{x+6y}\) |
| 4. \(f(x,y) = (x^2-5y^2) e^x\) |
| 5. \(f(x,y) = (x^2 - 5y^2) \left(\frac{1}{3y}+4\right)\) |
| 6. \(f(x,y) = x\) |
| 7. \(f(x,y) = 6\) |
| 8. \(f(x,y) = \ln (xy+2x-6y) \) |
| 9. \(f(x,y) = \frac{x^2-5y^2}{y^4-5x^4}\) |
| 10. \(f(x,y) = e^{\sqrt{x-4y}} (x-4y)\) |
| 11. \(f(x,y) = y^5 e^x\) |
| 12. \(f(x,y) = \frac{1}{16xy}\) |
| 13. \(f(x,y) = (x+e^y)^7\) |
| 14. \(f(x,y) = x^4 + 4x^3y - 6x^2y^2 - 4xy^3 + y^4\) |
| 15. \(f(x,y) = \sqrt{x+\sqrt{y}}\) |
| 16. \(f(x,y) = x^2y^3-4x^3\) |
Aquí hay una tabla que muestra la función\(A(t,r)\)
| \(\overset{t}{\downarrow} \ r\rightarrow\) |
.03 |
.04 |
.05 |
.06 |
.07 |
|
1 |
30.45 |
40.81 |
51.27 |
61.84 |
72.51 |
|
2 |
61.84 |
83.29 |
105.17 |
127.50 |
150.27 |
|
3 |
94.17 |
127.50 |
161.83 |
197.22 |
233.68 |
a. Estimación\(A_t (2, .05)\).
b. Estimación\(A_r (2, .05)\)
c. Usa tus respuestas a las partes a y b para estimar el valor de\(A (2.5, .054)\)
d. Los valores de la tabla provinieron de\(A(t,r)=1000 (e^{rt} - 1)\), que muestra los intereses devengados si se depositan 1000 dólares en una cuenta que gana r intereses anuales, se compone continuamente, y se deja ahí por\(t\) años. ¿Qué tan cerca están tus estimaciones de las partes a, b y c?
18. Aquí hay una tabla que muestra los valores para la función\(H(t,h)\).
| \(\overset{t}{\downarrow} \ h\rightarrow\) |
100 |
150 |
200 |
|
0 |
100 |
150 |
200 |
|
1 |
110.1 |
160.1 |
210.1 |
|
2 |
110.4 |
160.4 |
210.4 |
|
3 |
100.9 |
150.9 |
200.9 |
|
4 |
81.6 |
131.6 |
181.6 |
|
5 |
52.5 |
102.5 |
152.5 |
a. Estimar el valor de\(\frac{\partial H}{dt}\) at (3, 150).
b. Estimar el valor de\(\frac{\partial H}{dh}\) at (3, 150).
c. Usa tus respuestas a las partes a y b para estimar el valor de\(H(2.6, 156)\).
d. De los valores en la tabla provinieron\(H (t,h) = h + 15t - 4.9t^2\), lo que da la altura en metros sobre el suelo después de\(t\) segundos de un objeto que es arrojado hacia arriba desde una altura inicial de\(h\) metros con una velocidad inicial de 15 metros por segundo. ¿Qué tan cerca están tus estimaciones de las partes a, b y c?
Dada la función\(f(x,y) = x^2\sqrt{y}\)
a. Calcular\(f(2,4)\),\(f_x (2,4)\), y\(f_y(2,4)\)
b. Usa tus respuestas de parte\(a\) para estimar\(f(1.9, 4.1)\)
Dada la función\(f(x,y) = \ln (10 - x^2 - y)\)
a. Calcular\(f(2,5)\),\(f_x (2,5)\), y\(f_y(2,5)\)
b. Usa tus respuestas de parte\(a\) para estimar\(f(1.8,4.8)\)
En los problemas 21 - 26, utilice la gráfica de contorno mostrada para estimar el valor deseado.
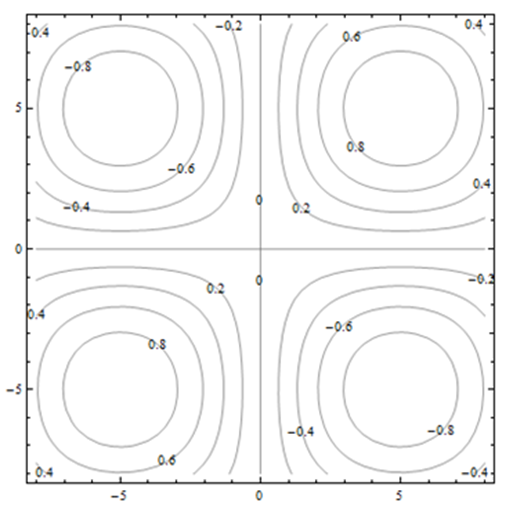
| 21. \(f_x(1,-5)\) |
| 22. \(f_x(-5,2)\) |
| 23. \(f_x(5,5)\) |
| 24. \(f_x(0,0)\) |
| 25. \(f_y(1,-5)\) |
| 26. \(f_y(-5,2)\) |
4.3 Ejercicios
Para los problemas del 1 al 6\(f_{xx}\), find\(f_{yy}\),,\(f_{xy}\) y\(f_{yx}\) para la función dada. Confirme eso\(f_{xy} = f_{yx}\).
| 1. \(f(x,y) = x^2-5y^2\) |
| 2. \(f(x,y) = x^4+4x^3y-6x^2y^y-4xy^3+y^4\) |
| 3. \(f(x,y) = 5x^2y^2\) |
| 4. \(f(x,y) = e^{x+6y}\) |
| 5. \(f(x,y) = \ln (xy + 2x - 6y)\) |
| 6. \(f(x,y) = \frac{x^2}{y^4-5}\) |
Encuentra los puntos críticos\(f(x,y) = y^3 - x^3 + 15x^2 - 12y + 12\) y usa la Prueba de Segunda Derivada para clasificarlos. Si la prueba falla, di “la prueba falla”.
Encuentra los puntos críticos\(f(x,y) = 2xy-x^2-2y^2+6x+4\) y usa la Prueba de Segunda Derivada para clasificarlos. Si la prueba falla, di “la prueba falla”.
Encuentra los puntos críticos\(f(x,y)=y^2-4 \ln (x) + 4x\) y usa la Prueba de Segunda Derivada para clasificarlos. Si la prueba falla, di “la prueba falla”.
Encuentra los puntos críticos\(f(x,y)= xy - 6x^2 + 3x -y+2\) y usa la Prueba de Segunda Derivada para clasificarlos. Si la prueba falla, di “la prueba falla”.
El origen es un punto crítico para la función\(f(x,y) = x^3+y^3\), y\(D = 0\) ahí. Es decir, falla la Prueba de Segunda Derivada. Usa lo que sabes sobre formas de funciones para decidir si hay un mínimo local, un máximo local o un punto de sillín para esta función en (0, 0).
El origen es un punto crítico para la función\(f(x,y) = 15 - x^2y^2\), y\(D = 0\) ahí. Es decir, falla la Prueba de Segunda Derivada. Usa lo que sabes sobre formas de funciones para decidir si hay un mínimo local, un máximo local o un punto de sillín para esta función en (0, 0).
Para los problemas del 13 al 18, encuentre todos los máximos locales, mínimos y puntos de sillín para la función.
| 13. \(f(x,y) = xy -5x^2 - 5y^2 + 33y\) |
| 14. \(f(x,y) = 10xy-x^2-y^2+3x\) |
| 15. \(f(x,y) = x^3+y^3-3xy\) |
| 16. \(f(x,y) = 5x^2-4xy+2y^2+4x-4y+10\) |
| 17. \(f(x,y) = y^2e^x+x^2\) |
| 18. \(f(x,y) = xy+2x-\ln (x^2y)\), para\(x>0\) y\(y>0\). |
A continuación se detallan las funciones de demanda para dos productos. \(p_1\),\(p_2\)\(q_1\), y\(q_2\) son los precios (en dólares) y cantidades de los productos 1 y 2.
\[q_1 = 200+3p_1+p_2 \nonumber\]
\[q_2=150+p_1+2p_2\nonumber\]
a. ¿Estos dos productos son bienes complementarios o sustitutivos?
b. ¿Cuál es la cantidad demandada por cada uno cuando el precio del producto 1 es de $20 por artículo y el precio del producto 2 es de $30 por artículo?
c. Escribir una función\(R(p_1,p_2)\) que exprese los ingresos totales de estos dos productos.
d. Encuentre el precio y la cantidad de cada producto que maximice los ingresos totales.
A continuación se detallan las funciones de demanda para dos productos. \(p_1\),\(p_2\)\(q_1\), y\(q_2\) son los precios (en dólares) y cantidades de los productos 1 y 2.
\[q_1 = 350+p_1+2p_2 \nonumber\]
\[q_2=225+p_1+p_2\nonumber\]
a. ¿Estos dos productos son bienes complementarios o sustitutivos?
b. ¿Cuál es la cantidad demandada por cada uno cuando el precio del producto 1 es de $20 por artículo y el precio del producto 2 es de $30 por artículo?
c. Escribir una función\(R(p_1,p_2)\) que exprese los ingresos totales de estos dos productos.
d. Encuentre el precio y la cantidad de cada producto que maximice los ingresos totales.
Supongamos que las funciones de demanda para dos productos son\(q_1 = f(p_1, p_2)\) y\(q_2 = g(p_1, p_2)\)\(p_1\), dónde\(p_2\),\(q_1\),, y\(q_2\) son los precios (en dólares) y las cantidades para los productos 1 y 2. Considerar las cuatro derivadas parciales\(\frac{\partial q_1}{\partial p_1}\),\(\frac{\partial q_1}{\partial p_2}\),\(\frac{\partial q_2}{\partial p_1}\), y\(\frac{\partial q_2}{\partial p_2}\). Dígale el signo de cada una de estas derivadas parciales si
a. los productos son bienes complementarios.
b. los productos son productos sustitutivos.