2.14: Proyecto- Definición Dura de Problemas Derivados

Propósito del proyecto: Luchar a través de un problema de cálculo difícil pero importante.

Cada una de las siguientes es una definición difícil del problema derivado. A tu grupo se le asignará uno de los siguientes, y luego podrás presentar la solución a la clase. En cada caso, las “cosas en el cuadro de ejemplo” no es tu problema, pero míralo y ojalá te ayude con tu problema.

1. Vamos\(f(x) = x^4\). Usando la definición de la derivada, encuentra\(f'(x)\).
   \((x + 1)^4\)Simplifica.Podemos hacer este problema dividiéndolo en\((x + 1)^2 (x + 1)^2\). Sabemos\((x + 1)^2 = x^2 + 2x + 1\), eso significa

   \((x + 1)^4 = (x^2 + 2x + 1)(x^2 + 2x + 1)\)

   Para resolver a partir de aquí, necesitamos multiplicar cada término de\((x^2 + 2x + 1)\) por\(x^2\), luego cada término por\(2x\), luego cada término por\(1\), y sumarlo todo. Aquí vamos:

   \[\begin{align*} (x + 1)^4 & = (x^2 + 2x + 1)({\color{green} x^2} + {\color{red} 2x} + {\color{blue} 1}) \\ & = (x^2 + 2x + 1){\color{green}x^2} + (x^2 + 2x + 1){\color{red}2x} + (x^2 + 2x + 1){\color{blue}1} \\ & = {\color{green} x^4 + 2x^3 + x^2} + {\color{red}2x^3 + 4x^2 + 2x} + {\color{blue}x^2 + 2x + 1} \\ & = x^4 + 4x^3 + 6x^2 + 4x + 1. \end{align*}\]

2. Vamos\(f(x) = \sqrt{x}\). Usando la definición de la derivada, find\(f'(x)\) (que también se puede escribir\(\frac{d}{dx} f(x)\) o\(\frac{df}{dx}\)).
   Racionalizar el numerador de\(\frac{\sqrt{x + 1} - \sqrt{x}}{x}\).

   Para “racionalizar el numerador”, el truco es multiplicar arriba e abajo por lo que se conoce como el conjugado: es lo mismo que el numerador, solo se voltea el signo para que la resta se convierta en suma o viceversa. En este caso, el conjugado es\(\sqrt{x + 1} + \sqrt{x}\). Vemos

   \[\begin{align*} \frac{\sqrt{x + 1} - \sqrt{x}}{x} & = \frac{(\sqrt{x + 1} - \sqrt{x})}{(x)} \cdot \frac{(\sqrt{x + 1} + \sqrt{x})}{(\sqrt{x + 1} + \sqrt{x})}\\ & = \frac{(\sqrt{x + 1} - \sqrt{x})(\sqrt{x + 1} + \sqrt{x})}{(x)(\sqrt{x + 1} + \sqrt{x})} \\ & = \frac{(\sqrt{x + 1})^2 - (\sqrt{x})^2}{x(\sqrt{x + 1} + \sqrt{x})} \\ & = \frac{x+1 - x}{x(\sqrt{x + 1} + \sqrt{x})} \\ & = \frac{1}{x(\sqrt{x + 1} + \sqrt{x})} \end{align*}\]

   El numerador está ahora racionalizado.

3. Vamos\(f(x) = \sin(x)\). Usando la definición de la derivada, find\(f'(x)\) (que también se puede escribir\(\frac{d}{dx} f(x)\) o\(\frac{df}{dx}\)). Hay tres hechos que necesitamos para calcular este derivado:
   • \(\sin(A + B) = \sin(A) \cos(B) + \cos(A) \sin(B)\)
   • \(\lim_{h \to 0} \frac{\sin(h)}{h} = 1\)
   • \(\lim_{h \to 0} \frac{\cos(h) - 1}{h} = 0\)
   Encuentra\(\lim_{h \to 0} \cfrac{\sin(y + h) - \sin(y) \cos(h)}{h}\).

   En este ejemplo, utilizamos el primer hecho enumerado anteriormente para escribir\(\sin(y + h) = \sin(y) \cos(h) + \cos(y) \sin(h)\). Tenemos el problema original es igual a

   \[\begin{align*} & = \lim_{h \to 0} \frac{\sin(y) \cos(h) + \cos(y) \sin(h)- \sin(y) \cos(h)}{h} \\ & = \lim_{h \to 0} \frac{\cos(y) \sin(h)}{h} \\ & = \lim_{h \to 0} \frac{\sin(h)}{h} \cdot \cos(y) \\ & = 1 \cdot \cos(y) \\ & = \cos(y) \end{align*}\]

   Aviso hacia el final que usamos\(\lim_{h \to 0} \frac{\sin(h)}{h} = 1\).

4. Vamos\(f(x) = e^x\). Usando la definición de la derivada, find\(f'(x)\) (que también se puede escribir\(\frac{d}{dx} f(x)\) o\(\frac{df}{dx}\)). Usa el límite que encontramos en la tarea ayer:\(\lim_{h \to 0} \frac{e^h - 1}{h} = 1\).
   Ejemplo útil: Simplificar\(\frac{e^{x + 1} + e^1}{e^x + 1}\).

   Recordemos eso\(e^{x + 1} = e^x e^1\). De ahí que esto se convierta

   \[\begin{align*} \frac{e^{x + 1} + e^1}{e^x + 1} & = \frac{e^x e^1 + e^1}{e^x + 1} \\ & = \frac{e^1(e^x + 1)}{e^x + 1} \\ & = e^1 = e \end{align*}\]

5. Vamos\(f(x) = \frac{1}{x}\). Usando la definición de la derivada, find\(f'(x)\) (que también se puede escribir\(\frac{d}{dx} f(x)\) o\(\frac{df}{dx}\)).
   Simplificar\(\cfrac{\cfrac{1}{x + 1} - \cfrac{1}{x}}{x}\).

   En este ejemplo, queremos despejar a los denominadores de esta complicada fracción doble. Para ello, vamos a multiplicar por ambos denominadores:\(x(x + 1)\).

   \[\begin{align*} \cfrac{\cfrac{1}{x + 1} - \cfrac{1}{x}}{x} & = \cfrac{\left(\cfrac{1}{x + 1} - \cfrac{1}{x} \right)}{x} \cdot \frac{x(x + 1)}{x(x + 1)} \\ & = \cfrac{\left(\cfrac{1}{x + 1} - \cfrac{1}{x} \right)x(x + 1)}{(x)(x)(x + 1)} \\ & = \cfrac{\left(\cfrac{x(x + 1)}{x + 1} - \cfrac{x(x + 1)}{x} \right)}{x^2(x + 1)} \\ & = \cfrac{x - (x + 1)}{x^2(x + 1)} \\ & = \cfrac{-1}{x^2(x + 1)} \end{align*}\]

6. Vamos\(f(x) = \ln(x)\). Usando la definición de la derivada, find\(f'(x)\) (que también se puede escribir\(\frac{d}{dx} f(x)\) o\(\frac{df}{dx}\)). Vamos a necesitar los siguientes hechos:
   • 
   • 
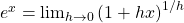
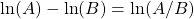
   • \(n \ln(A) = \ln(A^n)\)
   • \(\ln(e^x) = x\)
   (Ejemplo 1): Reescribir\(\frac{\ln(x+5) - \ln(x)}{2}\) como el logaritmo natural de una sola cantidad.

   Necesitamos usar algunas reglas de registro para simplificar esto. Primero usamos.

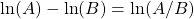   \[\begin{align*} \frac{\ln(x+5) - \ln(x)}{2} & = \frac{\ln\left(\frac{x+5}{x}\right)}{2} \\ & = \frac{\ln\left(1 + \frac{5}{x} \right)}{2} \end{align*}\]

   Ahora usamos\(n \ln(A) = \ln(A^n)\), pensando en la división por\(2\) como una multiplicación por.

   

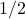   (Ejemplo 2): Simplificar.

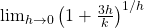   En este ejemplo, sabemos por nuestros hechos anteriores que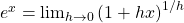. También vemos que

   

   Observe ahora que\(\frac{3}{k}\) está jugando el mismo papel que\(x\) en la\(e^x\) ecuación. Entonces esto simplifica a.
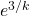