18.3: Clases, particiones y cocientes

Según se desee (ver Sección 18.1), se puede utilizar una relación de equivalencia para agrupar objetos equivalentes.

Ejemplo\(\PageIndex{1}\)

Considere\(\mathord{\equiv_5}\) en\(\mathbb{N}\text{.}\) Aviso que los elementos en cada uno de los siguientes conjuntos son todos equivalentes entre sí con respecto a\(\mathord{\equiv_5}\text{.}\)

\ begin {reunir*}\ {0, 5, 10, 15,\ ldots\}\\\ {1, 6, 11, 16,\ ldots\}\\\ {2, 7, 12, 17,\ ldots\}\\ {3, 8, 13, 18,\ ldots\}\\\ {4, 9, 14, 19,\ ldots\}\ end {recolector} Observe
también que\(\mathbb{N}\) es la unión disjunta de los conjuntos anteriores.

De hecho, podríamos hacer lo mismo por cada divisor\(n\text{,}\) no sólo porque\(n = 5\text{,}\) como\(\mathbb{N}\) es también la unión disjunta de los conjuntos

\ comenzar {reunir*}\ {\, 0,\, n,\, 2n,\, 3n,\,\ lpuntos\,\},\\\ {\, 1,\, n+1,\, 2n+1,\, 3n+1,\, 3n+1,\,\,\ lpuntos\,\},\\ {\, 2, n+2,\, 2n+2,\, 3n+2,\, 3n+2,\, 3n+2,\, 3n+2,\, 3n+2 +2,\,\ ldots\,\},\\\ vdots\\\ {\, n-1,\, n + (n-1),\, 2n + (n-1),\, 3n + (n-1),\,\ ldots\,\},\ end {gather*}
y nuevamente elementos en cada uno de los conjuntos anteriores son todos equivalentes entre sí con respecto a\(\mathord{\equiv_n}\text{.}\)

Definición: clase de equivalencia (de un elemento\(a\))

el subconjunto\(A\) consiste en todos los elementos que son equivalentes al elemento dado en relación con una\(a \in A\text{,}\) relación de equivalencia específica\(\mathord{\equiv}\) en,\(A\text{;}\) es decir, el conjunto

\ comenzar {ecuación*}\ {x\ en A\ vert x\ equiv a\}\ final {ecuación*}

Definición:\([a]\)

la clase de equivalencia del elemento\(a \in A\) relativo a alguna relación de equivalencia específica en\(A\)

Ejemplo\(\PageIndex{2}\): Equivalence classes of natural numbers modulo \(5\).

Si dividimos\(8\) por\(5\text{,}\) obtenemos\(1\) con\(3\) resto. Entonces la clase de equivalencia de\(8\) relativo a\(\mathord{\equiv_5}\) consiste en todos los números naturales que tienen resto\(3\) cuando se dividen por\(5\text{:}\)

\ begin {ecuación*} [8] =\ {3, 8, 13, 18,\ ldots\}\ texto {.} \ end {equation*}
Ahora,\(3\) está en esta clase porque cuando\(5\) dividimos\(3\) por obtenemos\(0\) con\(3\) resto. Pero si hubiéramos empezado con\(3\) en vez de\(8\text{,}\) habríamos dicho también que la clase de equivalencia de\(3\) relativo a\(\mathord{\equiv_5}\) consiste en todos los números naturales que tienen resto\(3\) cuando se dividen por\(5\text{:}\)

\ begin {ecuación*} [3] =\ {3, 8, 13, 18,\ ldots\}\ texto {.} \ end {ecuación*}

Proposición\(\PageIndex{1}\): Properties of equivalence classes.

Supongamos que\(\mathord{\equiv}\) es una relación de equivalencia en un conjunto no vacío\(A\text{.}\)

1. Por cada\(a \in A\text{,}\) que tenemos\(a \in [a]\text{.}\)
2. Porque\(a,a_1,a_2 \in A\) con\(a_1,a_2 \in [a]\text{,}\) tenemos\(a_1 \equiv a_2\text{.}\)
3. Para cada par\(a_1,a_2 \in A\text{,}\) tenemos\(a_1 \equiv a_2\) si y solo si\([a_1] = [a_2]\text{.}\)
4. Para cada par\(a_1,a_2 \in A\text{,}\) tenemos\(a_1 \not\equiv a_2\) si y solo si\([a_1] \cap [a_2] = \emptyset\text{.}\)

Prueba

Comprobante de Declaración 1.
Esta es solo la propiedad reflexiva,\(a \equiv a\text{.}\)

Comprobante de Declaración 2.
Si\(a_1,a_2 \in [a]\text{,}\) entonces por definición tenemos ambos\(a_1 \equiv a\) y\(a_2 \equiv a\text{.}\) Aplicando simetría a esta última equivalencia, podemos escribir\(a_1 \equiv a \equiv a_2\text{,}\) a lo que podemos aplicar la transitividad para obtener\(a_1 \equiv a_2\text{,}\) lo deseado.

Comprobante de Declaración 3.
(⇒)
Supongamos\(a_1 \equiv a_2\text{.}\) Para verificar\([a_1] = [a_2]\text{,}\) seguimos la Prueba para Establecer Igualdad. Primero, asumir\(x\) es un elemento arbitrario en\([a_1]\text{.}\)\(x \equiv a_1 \equiv a_2\text{,}\) Entonces así\(x \equiv a_2\) por la propiedad transitiva. Por lo tanto,\(x \in [a_2]\text{,}\) según se requiera. Esto demuestra que\([a_1] \subseteq [a_2]\text{;}\) el argumento a mostrar\([a_2] \subseteq [a_1]\) es casi exactamente el mismo, solo usando la propiedad simétrica para obtener primero\(a_2 \equiv a_1\text{.}\)

(⅓)
Por Declaración 1 de esta proposición, tenemos\(a_1 \in [a_1]\text{.}\) Si asumimos\([a_1] = [a_2]\text{,}\) entonces también tenemos\(a_1 \in [a_2]\text{,}\) lo que significa que\(a_1 \equiv a_2\text{,}\) según se requiera.

Comprobante de Declaración 4.
Probemos el equivalente “doble contrapositivo” bicondicional\(a_1 \equiv a_2 \Leftrightarrow [a_1] \cap [a_2] \ne \emptyset\text{.}\) (Ver Ejemplo Trabajado 2.1.2.)

(⇒)
Supongamos\(a_1 \equiv a_2\text{.}\) Entonces\([a_1] = [a_2]\) por la Declaración 3, entonces

\ begin {ecuación*} [a_1]\ cap [a_2] = [a_1]\ cap [a_1] = [a_1]\ text {.} \ end {equation*}
Pero no\([a_1]\) está vacío por la Declaración 1.

(⅓)
Supongamos\([a_1] \cap [a_2] \ne \emptyset\text{.}\) Entonces existe algún elemento\(x \in A\) que está en ambos\([a_1]\) y\([a_2]\text{,}\) para que ambos\(x \equiv a_1\) y\(x \equiv a_2\text{.}\) Por la propiedad simétrica, tenemos\(a_1 \equiv x\text{,}\) y combinando esto con\(x \equiv a_2\) en la propiedad transitiva da\(a_1 \equiv a_2\text{.}\)

La Declaración 3 de la Proposición nos\(\PageIndex{1}\) dice que cualquier miembro de una clase de equivalencia puede ser utilizado para definir la clase.

Definición: representante de clase de equivalencia

un elemento\(a \in A\) utilizado para definir la clase de equivalencia

\ begin {ecuación*} [a] =\ {x\ in A\ vert x\ equiv a\}\ fin {ecuación*}

Definición: conjunto completo de representantes de clase de equivalencia

un subconjunto para\(C \subseteq A\) que para cada uno\(x \in A\) exista exactamente uno\(a \in C\) para que\(x \in [a]\)

Recuerde que los elementos que son equivalentes entre sí en relación con alguna relación de equivalencia se consideran “esencialmente los mismos” desde el punto de vista de la propiedad utilizada para definir la relación de equivalencia. Por lo que los elementos diferentes pero equivalentes se vuelven intercambiables (ver Sección 18.1). Cuando tenemos un conjunto completo de representantes para las clases de equivalencia, estamos decidiendo intercambiar siempre un elemento por el representante elegido de la clase que contiene ese elemento.

Ejemplo\(\PageIndex{3}\): A complete set of equivalence class representatives for natural numbers modulo \(5\).

Continuando Ejemplo\(\PageIndex{2}\), podríamos representar la clase de números que tienen resto\(3\) por el número\(8\text{:}\)

\ begin {ecuación*} [8] =\ {3, 8, 13, 18,\ ldots\}\ texto {.} \ end {equation*}
Pero parece más “natural” representar esta clase por el número\(3\text{:}\)

\ begin {ecuación*} [3] =\ {3, 8, 13, 18,\ ldots\}\ texto {.} \ end {equation*}
Observe que cada uno de los números\(0,1,2,3,4\) tiene un resto diferente cuando se divide por\(5\text{,}\) lo que no hay dos de ellos equivalentes. Eso también significa que cada uno está en una clase diferente (Declaración 4 de la Proposición\(\PageIndex{1}\)). Pero cuando vamos más allá de\(4\text{,}\) los restos cuando se divide por\(5\) empezar a repetir: cada uno de los números en la lista\(5,6,7,8,9\) tiene el mismo resto que el número en la posición correspondiente en la lista\(0,1,2,3,4\text{.}\) Y luego los restos se repiten de nuevo cuando pasamos\(9\text{.}\) Y así sucesivamente. Entonces parece “natural” usar\(0,1,2,3,4\) como conjunto completo de representantes de las clases de equivalencia para\(\mathbb{N}\) módulo\(5\text{:}\)

\ begin {alinear*} [0] & =\ {0, 5, 10, 15,\ ldots\},\\ [1] & =\ {1, 6, 11, 16,\ ldots\},\\ [2] & =\ {2, 7, 12, 17,\ ldots\},\\ [3] & =\ {3, 8, 13, 18,\ ldots\},\\ [4] & =\ {4, 9, 14, 19,\ ldots\}. \ end {alinear*}

La definición de conjunto completo de representantes de clase de equivalencia supone implícitamente que las clases de equivalencia “llenan” todo el conjunto\(A\text{.}\) Pero ese siempre es precisamente el caso.

Definición: Partición

una colección de subconjuntos de un conjunto\(A\) que son disjuntos por pares y cuya unión es\(A\)

Definición: Celda de partición

uno de los subconjuntos que componen una partición de un conjunto

Figura\(\PageIndex{1}\): Diagrama que ilustra una partición de un conjunto, de manera que\(A = A_1 \sqcup A_2 \sqcup A_3 \sqcup \ldots \sqcup A_n\text{.}\)

Observación\(\PageIndex{1}\)

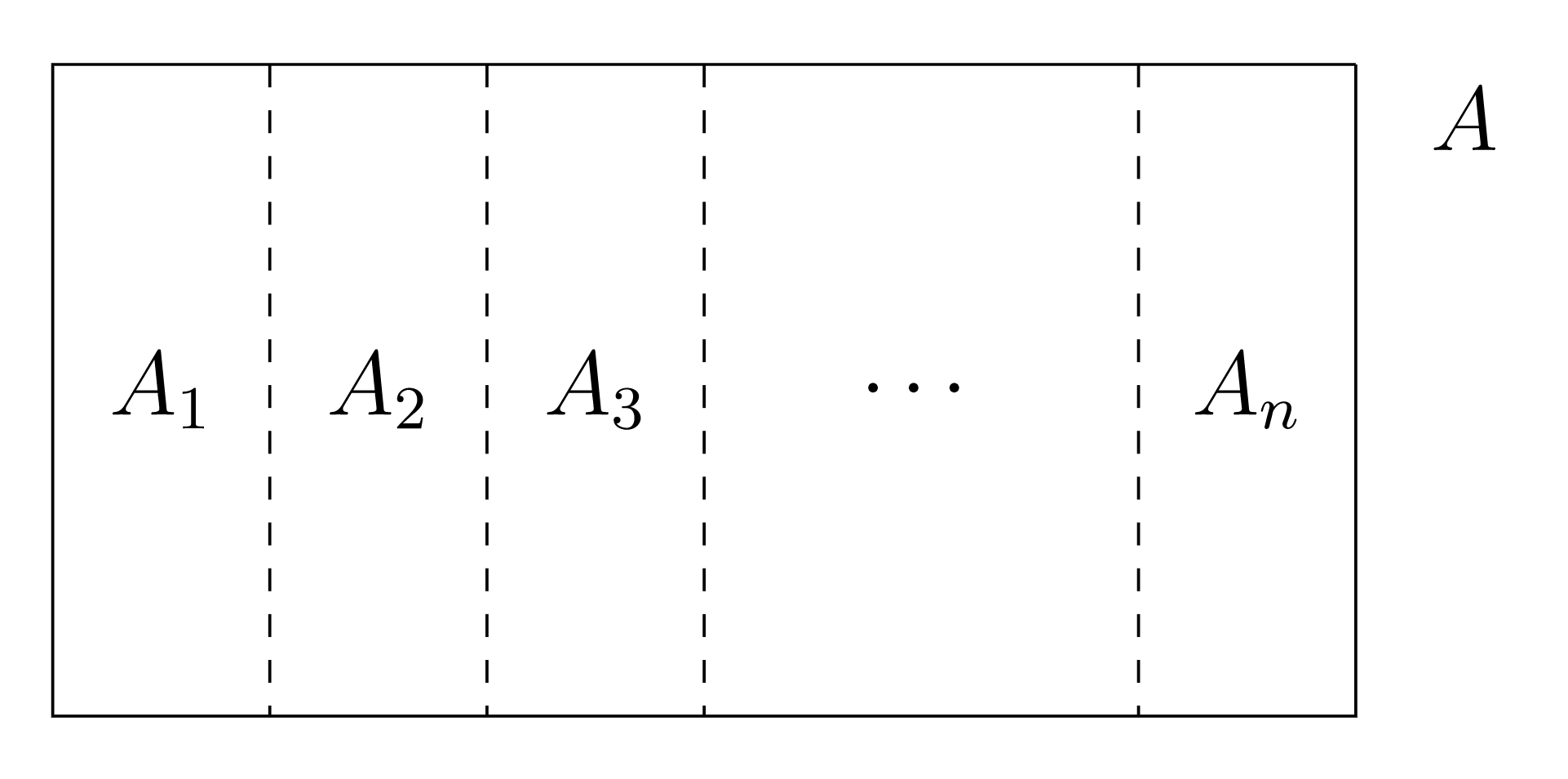
En esencia, la partición no es más que un sinónimo de unión disjunta. Entonces una colección de subconjuntos forman una partición cuando cada elemento del conjunto está exactamente en una celda de partición.

Nota\(\PageIndex{1}\)

No es necesario que una partición de un conjunto esté compuesta por un número finito (o incluso contable) de celdas; vea los ejemplos a continuación.

Teorema\(\PageIndex{1}\): Equivalence classes form a partition.

Si\(\mathord{\equiv}\) es una relación de equivalencia en un conjunto\(A\text{,}\), entonces las clases de equivalencia con respecto a\(\mathord{\equiv}\) son una partición de\(A\text{.}\)

Idea de prueba

Este teorema afirma que cada elemento de\(A\) está en exactamente una clase de equivalencia. Pero esto se desprende de las declaraciones de Proposición\(\PageIndex{1}\).

Ejemplo\(\PageIndex{4}\): Equivalence classes modulo \(n\).

Generalizando Ejemplo\(\PageIndex{3}\), cada uno de los números\(0,1,2,3,\ldots,n-1\) es su propio resto cuando se divide por\(n\text{.}\) Y luego el patrón de restos se repite, comenzando de nuevo en el resto\(0\text{,}\) cuando continuamos a los números\(n,n+1,\ldots\text{.}\) Así\(0,1,2,3,\dots,n-1\) es un conjunto completo de representantes de clase de equivalencia , y la\(n\) partición de módulo classes\(\mathbb{N}\) en los subconjuntos disjuntos

\ begin {alinear*} [0] & =\ {\, 0,\, n, 2n,\, 3n,\,\ ldots\,\},\\ [1] & =\ {\, 1,\, n+1, 2n+1,\, 3n+1,\, 3n+1,\,\ ldots\,\},\ [2] & =\ {\, 2,\, n+2, 2n+2,\, 3n+2,\,\ lpuntos\,\},\\ fantasma {[0]} &\ vdots\\ [n-1] & =\ {\, n-1,\, 2n-1, 3n-1,\, 4n-1,\, 4n-1,\,\ lpuntos\,\}. \ end {alinear*}

Ejemplo\(\PageIndex{5}\)

Dejar\(\scr{L}\) ser el conjunto de todas las líneas en el plano, y considerar\(\ell_1 \equiv \ell_2\) si\(\ell_1, \ell_2\) son paralelas. Después\(\mathord{\equiv}\) particiona\(\scr{L}\) en conjuntos de líneas paralelas.

Ejemplo\(\PageIndex{6}\)

Recordemos que para alfabeto\(\Sigma\text{,}\)\(\Sigma^\ast_n\) es el subconjunto de\(\Sigma^\ast\) que consiste en todas las palabras cuya longitud es exactamente\(n\text{.}\) Entonces

\ begin {ecuación*}\ Sigma^\ ast_0,\ Sigma^\ ast_1,\ Sigma^\ ast_2,\ ldots\ end {ecuación*}
es una partición de\(\Sigma^\ast\text{.}\) (Ver Ejercicio 9.9.9.)

Recordemos que una relación sobre se\(\Sigma^\ast\) puede definir como un subconjunto de\(\Sigma^\ast \times \Sigma^\ast\text{.}\) Así que considere la relación\(R\) en\(\Sigma^\ast\) definida por

\ begin {ecuación*} R\;\; =\;\; (\ Sigma^\ ast_0\ veces\ Sigma^\ ast_0)\;\;\ sqcup\;\; (\ Sigma^\ ast_1\ veces\ Sigma^\ ast_1)\;\;\ sqcup\;\; (\ Sigma^\ ast_2\ veces\ Sigma^\ Sigma^\ ast_2)\;\;\ sqcup\;\;\ ldots\ end {ecuación*}
Entonces\(R\) es la relación de equivalencia en\(\Sigma^\ast\) donde\(w \mathrel{R} y\) si \(\vert w \vert = \vert y \vert\text{,}\)y sus clases de equivalencia son precisamente los conjuntos\(\Sigma^\ast_n\text{,}\)\(n\ge 0\text{.}\)

Teorema\(\PageIndex{2}\): Partitions arise from equivalence relations.

Dada una partición de un conjunto\(A\text{,}\) existe una relación de equivalencia\(\mathord{\equiv}\) en\(A\) cuyas clases de equivalencia son precisamente las celdas de la partición.

Idea de Prueba.

Dada una partición de\(A\text{,}\) para cada uno\(a \in A\) existe exactamente una celda de partición\(a\text{.}\) que contiene So define\(a_1 \equiv a_2\) para significar “los elementos\(a_1,a_2\) están contenidos en la misma celda de partición de\(A\text{.}\)”

Observación\(\PageIndex{2}\)

Teorema\(\PageIndex{1}\) y Teorema se\(\PageIndex{2}\) combinan para proporcionar, para cada conjunto,\(A\text{,}\) una correspondencia biyectiva

\ begin {ecuación*}\ {\ text {relaciones de equivalencia sobre} A\}\;\;\ longleftrightarrow\;\;\;\ {\ text {particiones de} A\}. \ end {ecuación*}

Ejemplo\(\PageIndex{7}\): Determining an equivalence relation from a partition.

Determinar una relación de equivalencia explícita\(\mathord{\equiv}\) sobre\(\mathbb{Z}\) la cual las clases de equivalencia dan la siguiente partición.

\ begin {ecuación*}\ mathbb {Z}\;\;\; =\;\;\ ldots\;\;\ sqcup\;\;\ {-3, -2, -1\}\;\;\ sqcup\;\;\\ sqcup\;\\\ sqcup\;\\\ sqcup\;\ {3, 4, 5\}\;\;\ sqcup\;\;\ lpuntos\ final {ecuación*}

Solución

Observe que cada celda de la partición contiene un múltiplo de\(3\) junto con los siguientes dos enteros consecutivos. Entonces, una manera de definir explícitamente la relación de equivalencia correspondiente es: para\(a,b \in \mathbb{Z}\text{,}\) definir\(a \equiv b\) para ser verdadero si existe\(n \in \mathbb{Z}\) tal que\(3 n \le a,b \le 3 n + 2\text{.}\) (Nota: Se omiten los detalles que muestran que esta es una relación de equivalencia.)

Definición: Cociente (de un conjunto\(A\) relative to an equivalence relation \(\mathord{\equiv}\))

el subconjunto de\(\mathscr{P}(A)\) cuyos elementos son las clases de equivalencia de\(\mathord{\equiv}\)

Definición:\(A / \mathord{\equiv} \)

el cociente de\(A\) relación relativa a equivalencia\(\mathord{\equiv}\text{,}\) para que

\ begin {ecuación*} (A/\ mathord {\ equiv}) =\ {[a]\ vert a\ en A\}\ end {ecuación*}

Ejemplo\(\PageIndex{8}\): A quotient described by class representatives.

Considerar la partición\(\mathbb{Z}\) de de Ejemplo Trabajado\(\PageIndex{7}\), y la relación de equivalencia correspondiente\(\mathrel{\equiv}\text{.}\) Para describir solo\(\mathbb{Z} / \equiv\text{,}\) necesitamos escoger un representante de cada clase. La forma más obvia en este caso es

\ begin {ecuación*} (\ mathbb {Z}/\ mathord {\ equiv}) =\ {\ ldots, [-3], [0], [3], [6],\ ldots\}\ text {.} \ end {ecuación*}

Ejemplo\(\PageIndex{9}\): Determining a quotient.

Dejar\(\mathord{\equiv}\) representar la relación de equivalencia en\(\mathbb{Z}\) definido por

\(0 \equiv 0\text{,}\)y

para no cero\(m,n \in \mathbb{Z}\text{,}\)

\ begin {align*} m &\ equiv n & &\ text {if} &\ dfrac {m} {\ vert m\ vert} & =\ dfrac {n} {\ vert n\ vert}\ text {.} \ end {alinear*}

Determinar la partición y cociente correspondientes de\(\mathbb{Z}\text{.}\)

Solución

Primer aviso que\(0\) estará en una clase de equivalencia por sí sola. A continuación, considere los valores que posiblemente\(m/\vert m \vert\) puedan tomar.

Si\(m \gt 0\text{,}\) entonces es\(\vert m \vert = m\) así\(m/\vert m \vert = 1\text{.}\)

Si\(m \lt 0\text{,}\) entonces es\(\vert m \vert = - m\) así\(m/\vert m \vert = -1\text{.}\)

Entonces esta relación de equivalencia es sólo una forma elegante de decir que\(m,n\) tienen el mismo signo. Por lo tanto, todos los números positivos estarán en la misma clase de equivalencia, y todos los números negativos estarán en la misma clase de equivalencia. Ahora tiene sentido que\(0\) esté en una clase por sí misma, ya que no\(0\) es ni positivo ni negativo. La partición de\(\mathbb{Z}\) correspondiente a\(\mathord{\equiv}\) es entonces

\ begin {ecuación*}\ mathbb {Z}\;\; =\;\;\;\ {\ ldots, -3, -2, -1\}\;\;\ sqcup\;\;\ {0\}\;\;\ sqcup\;\;\ {1, 2, 3,\ ldots\}\ text {.} \ end {equation*}
Para describir solo\(\mathbb{Z} / \mathord{\equiv}\text{,}\) necesitamos escoger un representante de cada clase de equivalencia. Una posibilidad es

\ begin {ecuación*}\ mathbb {Z} = [-1]\ sqcup [0]\ sqcup [1]\ text {,}\ end {ecuación*}
para que

\ begin {ecuación*} (\ mathbb {Z}/\ mathord {\ equiv}) =\ {[-1], [0], [1]\}\ text {.} \ end {ecuación*}

Definición: proyección natural (en un conjunto\(A\) relative to an equivalence relation \(\mathord{\equiv}\))

la función\(A \to (A / \mathord{\equiv})\) definida por\(a \mapsto [a]\)

Nota\(\PageIndex{2}\)

La proyección natural siempre\(A \to (A / \mathord{\equiv})\) es suryectiva, pero casi nunca es inyectiva.

Ejemplo\(\PageIndex{10}\): Natural projection modulo-\(5\).

Recordemos que\(\mathord{\equiv}_5\) representa la relación módulo-\(5\) equivalencia en\(\mathbb{N}\text{.}\) En Ejemplo\(\PageIndex{3}\) determinamos que hay cinco clases de equivalencia, representadas por elementos de\(0,1,2,3,4\text{,}\) manera que

\ begin {ecuación*} (\ mathbb {N}/\ mathord {\ equiv} _5) =\ {[0], [1], [2], [3], [4]\}\ text {.} \ end {equation*}
A continuación se presentan algunos ejemplos de imágenes de elementos bajo la proyección natural.

\ begin {align*} 2 &\ mapsto [2] & 7 &\ mapsto [2] & 104 &\ mapsto [4] & 76 &\ mapsto [1] & 2045 &\ mapsto [0]\ text {.} \ end {alinear*}