1.3: Prueba por Inducción
- Page ID
- 117397
Una breve exploración
Supongamos que estabas jugando con los cuadrados perfectos positivos más pequeños (una lista se encuentra en el Apéndice B), y decidiste buscar patrones en sus sumas. Podrías computar
\[\begin{aligned} 1 &= 1;\\ 5 &= 1+4;\\ 14 &= 1+4+9;\\ 30 &= 1+4+9+16;\\ 55 &= 1+4+9+16+25;\\ 91 &= 1+4+9+16+25+36;\\ 140 &= 1+4+9+16+25+36+49;\\ 204 &= 1+4+9+16+25+36+49+64.\end{aligned}\]
y preguntarse qué patrones existen en esta secuencia de “sumas de cuadrados”\[1,5,14,30,55,91,140,204,\dots.\nonumber \]
Al trazar estos números como puntos en el plano de coordenadas, es decir, trazar\((1,1), (2,5), (3,14), (4,30)\), etc., se obtiene la siguiente imagen:
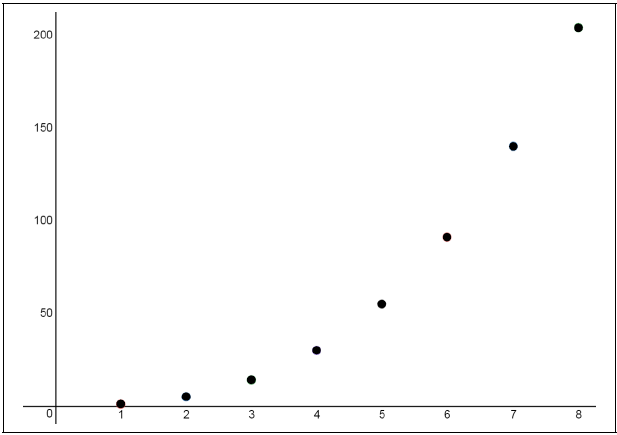
Desde un primer vistazo a la imagen, parece que los puntos ciertamente encajan en una curva suave, tal vez una parábola u otra curva polinómica, o tal vez la gráfica de una función exponencial. Una cosa que no sabemos es la ecuación de esta curva.
Al mirar\(1,5,14,30,55,91,140,204,\dots\) nuevamente los números de las sumas de cuadrados, y dirigirse quizás en una dirección diferente, podríamos ver sus factorizaciones principales: \(^{1}\)
\[\begin{aligned} 1 &\\ 5 &= 5;\\ 14 &= 2\cdot 7;\\ 30 &= 2\cdot 3 \cdot 5;\end{aligned}\]
\[\begin{aligned} 55 &= 5 \cdot 11;\\ 91 &= 7 \cdot 13;\\ 140 &= 2^2\cdot 5\cdot 7;\\ 204 &= 2^2 \cdot 3 \cdot 17.\end{aligned}\]
Una cosa que destaca de las factorizaciones son los números 5, 7, 11, 13 y 17. Aparte de las factorizaciones de 30 y 140 (donde no vemos 9 o 15), parece que el último número en cada factorización sucesiva es sólo el siguiente número impar. De hecho, si nos olvidamos de las factorizaciones prime y reescribimos las factorizaciones de 1, 30 y 140 anteriores, veríamos el patrón aún más claramente:
\[\begin{aligned} 1 &= \frac{1}{3}\cdot 3;\\ 5 &= 5;\\ 14 &= 2\cdot 7;\\ 30 &= \frac{1}{3} \cdot 2 \cdot 5 \cdot 9 ;\end{aligned}\]
\[\begin{aligned} 55 &= 5 \cdot 11;\\ 91 &= 7 \cdot 13;\\ 140 &= \frac{1}{3} \cdot 2^2\cdot 7\cdot 15;\\ 204 &= 2^2 \cdot 3 \cdot 17.\end{aligned}\]
Tenga en cuenta que para que 3, 9, y 15 aparezcan en los lugares esperados, tuvimos que introducir la fracción\(\frac{1}{3}\) frente a algunas de las líneas.
Pero ahora ¿podemos explicar los patrones en los otros factores que aparecen antes de los factores impares finales? ¿Podemos explicar por qué algunas líneas necesitan la fracción en el frente mientras que las otras no parecen? A través de una manipulación un poco inteligente y tal vez algo de suerte, podríamos pasar en las siguientes formas de escribir nuestros números de suma de cuadrados:
\[\begin{aligned} 1 &= \frac{1}{6} \cdot 1 \cdot 2 \cdot 3;\\ 5 &= \frac{1}{6} \cdot 2 \cdot 3 \cdot 5;\\ 14 &= \frac{1}{6} \cdot 3 \cdot 4 \cdot 7;\\ 30 &= \frac{1}{6} \cdot 4 \cdot 5 \cdot 9 ;\end{aligned}\]
\[\begin{aligned} 55 &= \frac{1}{6} \cdot 5 \cdot 6 \cdot 11;\\ 91 &= \frac{1}{6} \cdot 6 \cdot 7 \cdot 13;\\ 140 &= \frac{1}{6} \cdot 7 \cdot 8 \cdot 15;\\ 204 &= \frac{1}{6} \cdot 8 \cdot 9 \cdot 17.\end{aligned}\]
Definitivamente hay un patrón aquí. De hecho, mirando\[\begin{aligned} 1^2 &= \frac{1}{6} \cdot 1 \cdot 2 \cdot 3,\\ 1^2+2^2 &= \frac{1}{6} \cdot 2 \cdot 3 \cdot 5,\\ 1^2+2^2+3^2 &= \frac{1}{6} \cdot 3 \cdot 4 \cdot 7,\end{aligned}\] y así sucesivamente, podríamos adivinar que lo siguiente es cierto:
Si\(n\) es un entero positivo, entonces\[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \]
Trazando\(y=\frac{1}{6}x(x+1)(2x+1)\) en el plano de coordenadas, obtenemos una curva que pasa perfectamente por los puntos de nuestra gráfica desde antes, y como esperábamos, nuestra fórmula conjeturada para los números es un polinomio, es una función cúbica.
En este punto creemos que hemos descubierto una fórmula para la suma de los primeros números cuadrados\(n\) positivos. Sin embargo, aparte de apelar a nuestras observaciones (que rara vez es lo suficientemente bueno para un matemático), ¿cómo probaríamos que nuestra fórmula es correcta?
Pruebas por inducción matemática
Ahora discutimos una poderosa herramienta para responder preguntas como la anterior y para probar declaraciones sobre enteros. Esta herramienta reaparecerá en diversos lugares a lo largo de este texto. Es el Principio de Inducción Matemática introducido en el capítulo anterior, al que nos referiremos por PMI o simplemente inducción. Aquí está de nuevo, ligeramente reafirmado: \(^{2}\)
Si una declaración sobre enteros sacifica tanto
- la afirmación es verdadera para el número\(n_0\), y
- siempre que la afirmación sea cierta para cada uno de los números para\[n_0,\: n_0+1,\ldots ,k,\nonumber\] los que la declaración\(k + 1\) sea cierta también,
entonces la declaración es verdadera para un entero mayor que o igual a\(n_0\).
Hay mucho que digerir en este principio. Lo ilustramos con algunos ejemplos, señalando algunas características clave de la inducción en el camino.
Comenzamos con nuestra conjeturada declaración sobre las sumas de cuadrados. Llamamos a la declaración que queremos acreditar una proposición. También podría llamarse teorema, lema o corolario dependiendo de la situación. Aquí nuevamente está nuestra declaración.
Si\(n\) es un entero positivo, entonces\[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \]
Prueba
Al pensar en una prueba, esta afirmación parece un buen candidato para una prueba usando PMI. ¿Por qué es esto?
PMI es una técnica de prueba diseñada específicamente para declaraciones de la forma\[P(n)\text{ for all integers }n\geq n_0.\nonumber\] donde\(P(n)\) es una declaración dependiendo de un entero\(n\), y\(n_0\) es un entero específico.
Ahora la proposición anterior está escrita como una declaración “si/entonces”, pero puede reformularse como\[\text{``}1^2+2^2+\cdots +n^2=\frac{1}{6}n(n+1)(2n+1)\text{ for all integers }n\geq 1\text{''.}\nonumber\]
Esto lo convierte en un buen candidato para el PMI, y, usando la notación de la idea clave anterior, también nos dice dos cosas:
- \(P(n)\)es la declaración "\(\displaystyle 1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1)\)“;
- \(n_0 = 1\).
Antes de continuar, vale la pena señalar algunas cosas. En primer lugar,\(P(n)\) se utiliza la notación para sugerir que los valores de\(n\) pueden ser sustituidos en el\(P(n)\). Si\(n=1\) entonces nuestro\(P(n)\) se convierte\(P(1)\), es decir, la declaración\(1^2=\frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1)\), y si\(n=2\) entonces\(P(n)\) se convierte\(P(2)\), que es la declaración\(1^2+2^2 = \frac{1}{6}\cdot 2(2+1)(2\cdot 2 + 1)\).
A continuación, es importante señalar que\(P(n)\) es la ecuación completa, no simplemente\(1^2+2^2+\cdots+n^2\) o\(n^2\) o\(\frac{1}{6}n(n+1)(2n+1)\); en lugar de una expresión, es una declaración. Este será prácticamente siempre el caso: si has identificado correctamente lo que\(P(n)\) debería ser, entonces\(P(n)\) será una oración matemática completa, como una ecuación o desigualdad, pensó que a veces puede ser una oración en inglés más complicada, \(^{3}\) tal vez abarcando múltiples líneas.
Continuando hacia una prueba de nuestra proposición, ahora que hemos reconocido que el comunicado tiene una forma adecuada para usar PMI, y hemos identificado\(P(n)\) y\(n_0\), estamos listos para comenzar a armar una prueba. Una prueba por inducción muestra que\(P(n)\) satisface tanto las condiciones (a) como (b) en el Principio:
PMI (a) Explique por qué\(P(n_0)\) es cierto. \(^{4}\)
PMI (b) Justificar cuidadosamente lo siguiente: Si\(P(n)\) se sabe que es cierto para todos los valores de\(n\) tal que\(n_0\leq n\leq k\) y\(k\) es algún número entero, entonces estas afirmaciones implican que eso\(P(k +1)\) es cierto. Dicho de otra manera, lo que tenemos que probar es que\[\text{if }P(n_0);\: P(n_0 + 1);\: P(n_0 + 2);\ldots P(k)\text{ are all true, then }P(k + 1)\text{ must be true, too.}\nonumber\]
¿Cómo se ve este esquema para nuestra propuesta?
El paso PMI (a) requiere una demostración que\(P(n_0)\) sea verdadera. Para nosotros esto significa que debemos explicar por qué\(P(1)\) es cierto, es decir, por qué\[1^2 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1).\nonumber \] Dado que ambos lados de la ecuación son iguales a 1, esto puede verse inmediatamente como cierto; solo necesitamos declararlo en la prueba, y PMI (a) estará completo.
Ahora bien, como PMI (b) es una declaración si/entonces, para probarlo comenzamos asumiendo o suponiendo, solo por el bien del argumento,\[P(n) \text{ is true for } 1 \le n \le k.\nonumber \] que es decir, asumimos\[\label{ind_hyp} 1^2 + 2^2 + \cdots + n^2 = \frac{1}{6}n(n+1)(2n+1)\mbox { for } 1 \le n \le k.\]
Otra forma de decirlo es que suponemos que todas\[\begin{gathered} \nonumber 1^2 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1),\\ \nonumber 1^2+2^2 = \frac{1}{6}\cdot 2(2+1)(2\cdot 2 + 1),\\ \nonumber \vdots\\ \nonumber 1^2+2^2+\cdots+k^2 = \frac{1}{6}\cdot k(k+1)(2k + 1)\end{gathered}\] son afirmaciones verdaderas, y nos gustaría ver qué implicarían estas.
El supuesto\(\eqref{ind_hyp}\) se llama hipótesis de inducción; es la parte “si” de la “si/entonces” que estamos probando en PMI (b). Recuerde, para probar esta implicación, suponemos que\(P(n)\) se sabe que la afirmación es cierta para cada elección de\(n\) entre\(n_0\) y\(k\), y luego mostramos cómo usar estos hechos para probar que se\(P(n)\) mantiene cuando \(n=k+1\). Demostrar que eso\(P(k+1)\) es cierto a veces se llama el paso de inducción.
Aquí hay una manera de llevar a cabo el paso inductivo en nuestro ejemplo. Tomamos la ecuación\[1^2+2^2+\cdots+k^2=\frac{1}{6}k(k+1)(2k+1)\nonumber \] (que es\(P(k)\), una de las ecuaciones que acordamos suponer que era cierta en la hipótesis de inducción) y agregamos\((k+1)^2\) a ambos lados para obtener\[ \label{indeq1} 1^2+2^2+\cdots+k^2 + (k+1)^2=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2. \] Tenga en cuenta que estamos tratando de probar\(P(k+1)\), así que nos gustaría mostrar que \[1^2+2^2+\cdots+ (k+1)^2=\frac{1}{6}(k+1)(k+1+1)(2(k+1)+1);\nonumber \]aún no estamos del todo ahí. Las dos últimas ecuaciones anteriores sí coinciden en el lado izquierdo, lo cual es bueno, pero los lados de la derecha aún no son los mismos; ¿cómo justificaremos\(P(k+1)\)?
Aquí, todo lo que se necesita es una simple manipulación algebraica. Partiendo de la ecuación\(\eqref{indeq1}\), podemos escribir\[\begin{aligned} 1^2+2^2+\cdots+k^2 + (k+1)^2 &=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2\\ &= \frac{1}{6}k(k+1)(2k+1) + \frac{1}{6} \cdot 6(k+1)^2\\ &= \frac{1}{6}(k+1)\left[k(2k+1)+6(k+1)\right]\\ &= \frac{1}{6}(k+1)\left(2k^2+7k+6\right)\\ &= \frac{1}{6}(k+1)(k+2)(2k+3)\\ &= \frac{1}{6}(k+1)(k+1+1)(2(k+1)+1),\end{aligned}\] cuáles muestran que se\(P(k+1)\) pueden probar si sabemos que\(P(1),\cdots,P(k)\) son ciertos. Así hemos establecido PMI (b), y PMI nos dice que desde que PMI (a) y PMI (b) se mantienen, la afirmación\(P(n)\) es cierta para\(n\geq 1\). ¡Ya terminamos!
Resumiendo la discusión anterior, ahora damos una prueba menos pedagógica, más aerodinámica, que está más en línea con los tipos de pruebas por las que debes esforzarte.
Si\(n\) es un entero positivo, entonces\[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber\]
Prueba
Demostramos la proposición por inducción sobre la variable\(n\).
Cuando\(n=1\) nos encontramos\[1^2 = 1 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1),\nonumber \] así la ecuación reclamada es verdadera cuando\(n=1\).
Supongamos que\[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1) \quad \text{for }1 \leq n \leq k \quad \text{(the induction hypothesis)}.\nonumber \] tomando\(n = k\) tenemos\[1^2+2^2+\cdots+k^2 = \frac{1}{6}k(k+1)(2k+1).\nonumber \] Entonces\[\begin{aligned} 1^2+2^2+\cdots+(k+1)^2 &= \left[1^2+2^2+\cdots+k^2\right] + (k+1)^2 \\ &=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2 \quad \mbox { (by the induction hypothesis)}\\ &= \frac{1}{6}k(k+1)(2k+1) + \frac{1}{6} \cdot 6(k+1)^2\\ &= \frac{1}{6}(k+1)\left[k(2k+1)+6(k+1)\right]\\ &= \frac{1}{6}(k+1)\left(2k^2+7k+6\right)\\ &= \frac{1}{6}(k+1)(k+2)(2k+3)\\ &= \frac{1}{6}(k+1)(k+1+1)(2(k+1)+1).\end{aligned}\]
De ahí por PMI concluimos que\[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \] para\(n\geq 1\).
Una de las señas de identidad de una prueba escrita correctamente por inducción es que si verificamos el reclamo dejando\(n\) igual a cada entero a partir de\(n_0\), a su vez, en\(P(n)\), la prueba debería darnos una justificación convincente a través de un efecto “dominó”. Por ejemplo, en la proposición anterior, nos identificamos\(n_0\) como 1; ¿justifica la prueba\(P(1)\)? Sí, esto es lo que explicó la segunda oración.
Ahora, ¿justifica la prueba\(P(2)\)? Considera el resto de la prueba. Empezamos por tomar como un hecho que todos\(P(1),\cdots,P(k)\) son ciertos. Bueno, por el momento solo sabemos que eso\(P(1)\) es cierto, así que sólo podemos suponer que\(P(1),\cdots,P(k)\) son todos ciertos si\(k=1\) y la lista\(P(1),\cdots,P(k)\) realmente solo contiene\(P(1)\). Entonces leamos el resto de la prueba, sustituyendo\(1\) por todas partes que veamos\(k\). Las oraciones restantes en el comprobante nos dan un procedimiento de prueba\(P(k+1)\), lo que para nosotros significa\(P(2)\). Entonces sí, la prueba sí justifica\(P(2)\).
Ahora, ¿justifica la prueba\(P(3)\)? Volvamos a la mitad de la prueba y releamos la prueba a partir de la hipótesis de inducción. Ahí se supone que partimos de la afirmación que\(P(1),\cdots,P(k)\) son todas ciertas. Ya que en este punto nos hemos convencido de que\(P(1)\) y ambos\(P(2)\) son ciertos, ahora podemos dejar\(k=2\) y sustituir\(2\) por todas partes que veamos\(k\). Entonces prueban las sentencias restantes en la prueba\(P(k+1)\), lo que para nosotros en este punto significa\(P(3)\), por lo que la prueba sí justifica\(P(3)\).
Continuar con este proceso, releer la prueba una y otra vez, nos permite permitir justificada y lógicamente\(k\) ser cada vez más grandes en la hipótesis de inducción, y vemos que si volvemos a aplicar la parte de la prueba comenzando la hipótesis de inducción suficientes veces, tendríamos una prueba de \(P(n)\)no importa cuál número entero finito (pasado\(n_0\))\(n\) pasó a ser. Es por ello que la inducción demuestra que eso\(P(n)\) es cierto para cualquiera\(n \geq n_0\).
A continuación se presenta otro ejemplo de una prueba usando PMI. Esta vez el enunciado\(P(n)\) es una desigualdad, y el valor no\(n_0\) es 1. Intenta elaborar una prueba propia antes de leer la prueba presentada aquí.
Si\(n \ge 5\) entonces\(2^n>5n\).
Prueba
Demostramos la proposición por inducción sobre la variable\(n\). Si\(n=5\) tenemos\(2^5>5 \cdot 5\) o\(32>25\) que es verdad.
Supongamos\[2^n>5n \quad \text{ for }5 \leq n \leq k \quad \text{(the induction hypothesis)}.\nonumber \]
Tomando\(n = k\) tenemos\[2^k>5k.\nonumber \] Multiplicando ambos lados por 2 da\[2^{k+1}>10k.\nonumber \] Ahora\(10k=5k+5k\) y\(k\geq 5\) así\(k\geq 1\) y por lo tanto\(5k\geq 5\). De ahí\[10k=5k+5k\geq 5k+5=5(k+1).\nonumber \] se deduce que\[2^{k+1}>10k\geq 5(k+1)\nonumber \] y por lo tanto\[2^{k+1}>5(k+1).\nonumber \]
De ahí por PMI concluimos que\(2^n>5n\) para\(n\geq 5\).
Tenga en cuenta que en Proposición\(\PageIndex{3}\) la condición\(n \geq 5\) (que nos lleva a tener\(n_0=5\)) es necesaria, ya que\(2^5 > 5\cdot 5\), pero\(2^4 < 5\cdot 4\).
Considerando ambas proposiciones anteriores, algunos comentarios generales pueden ayudar. Primero, tenga en cuenta que la versión terminada de una prueba por inducción suele ser mucho más concisa y directa que los cálculos y notas que se utilizaron para encontrarla. Por esa razón, las pruebas de inducción en textos como este pueden parecer un poco más misteriosas de lo necesario, pero para la mayoría de los matemáticos, la concisión es preferible, y harías bien en intentar incluir solo las necesidades en tus pruebas cuando las estés puliendo.
A continuación, y lo que es más importante, ¿cómo averiguamos qué hacer para probar\(P(k+1)\) una vez que habíamos supuesto que eso\(P(n)\) era cierto\(n_0\leq n \leq k\)? Este es el gran reto de la inducción matemática, y el único lugar donde las pruebas por inducción requieren resolución de problemas y a veces algo de creatividad o ingenio. Se requirieron diferentes pasos en esta etapa de las pruebas de las dos proposiciones anteriores, y averiguar cómo mostrar que eso sucede\(P(k+1)\) automáticamente si\(P(n_0), \dots, P(k)\) no es una ciencia exacta.
Una de las mejores cosas para tratar es escoger una parte de la declaración\(P(k+1)\) que parezca algo de una de las declaraciones anteriores\(P(n_0), \cdots, P(k)\), y tratar de concluir algo sobre esa parte de\(P(k+1)\).
En la prueba de Proposición\(\PageIndex{2}\), por ejemplo, el lado izquierdo de\(P(k+1)\) incluyó todos los términos del lado izquierdo de\(P(k)\) y un término más además, y fue esta conexión con la ecuación la\(P(k)\) que hizo probar \(P(k+1)\)posible. En la prueba de Proposición\(\PageIndex{3}\), la desigualdad\(P(k+1)\) tenía un lado izquierdo que incluía\(2^{k+1}\). Esto no coincidía con el lado izquierdo de ningún otro\(P(5), \dots, P(k)\), pero estuvo bastante cerca de la\(2^k\) aparición en el lado izquierdo de\(P(k)\). Usar la desigualdad\(2^k > 5k\) de\(P(k)\) para tratar de decir algo sobre el\(2^{k+1}\) in\(P(k+1)\) es lo que nos motivó a multiplicar ambos lados de\(P(k)\) por 2, consiguiendo\(2^{k+1}>10k\) como lo hicimos.
Esto puede que aún no aclare completamente cómo usar\(P(n)\) declaraciones anteriores para probar\(P(k+1)\), pero es un punto de partida, y probar\(P(k+1)\) en PMI (b) se volverá mucho más claro y fácil con la práctica. Nuevamente, escoge una parte de la declaración\(P(k+1)\) que parezca algo de una de las declaraciones anteriores\(P(n)\), e intenta concluir algo sobre el resto de\(P(k+1)\).
Por último, notarás que había algunas cosas comunes a las pruebas de las Proposiciones\(\PageIndex{2}\) y \(\PageIndex{3}\)que no se detallaban en el esquema simplificado para las pruebas de inducción de antes. Ahora damos un esquema más detallado para las pruebas por inducción, seguido de ejercicios donde puedes practicar aplicarlo.
- Primero exponga qué proposición va a demostrar. Preceden a la declaración por Proposición, Teorema, Lema, Corolario, Hecho, o Para Probar:.
- Escribe el Comprobante o Pf. al comienzo mismo de tu comprobante.
- Di que vas a usar la inducción (¡no todas las pruebas matemáticas usan inducción!) y si no resulta evidente a partir del enunciado de la proposición, identificar claramente\(P(n)\), es decir, la afirmación a probar y la variable de la que depende, y el valor inicial\(n_0\). A pesar de que esto suele ser claro, a veces estas cosas pueden no ser obvias. Y, por supuesto, la variable no necesita serlo\(n\).
- Demostrar que se\(P(n)\) sostiene cuando\(n = n_0\).
- Supongamos que\(P(n)\) se sostiene para\(n_0\leq n\leq k\). (¡Exponga esta suposición por escrito, siguiendo de cerca la forma en los ejemplos aquí!) Esta suposición será referida como la hipótesis de inducción.
- Utilice la hipótesis de inducción y cualquier otra cosa que se sepa que es cierta para probar que se\(P(n)\) sostiene cuando\(n = k + 1\).
- Concluir, quizá por escrito, que desde que se han cumplido las condiciones del PMI,\(P(n)\) sostiene para\(n\geq n_0\).
- Escribe QED,\(\square\),\(\blacksquare\),\(//\) o algo así para indicar que has completado tu comprobante.
Ejercicios
Considera la siguiente declaración:
Cada entero no negativo se puede escribir como la suma de cuatro cuadrados perfectos.
En este ejercicio imaginaremos cómo sería una prueba de esta afirmación por inducción, si una fuera posible.
- Para esta declaración, conteste estas preguntas (provenientes de la Parte 3 de las ocho partes principales al final de la sección): ¿Cuál\(n_0\) sería? ¿Qué\(P(n)\) sería? (Recuerde que\(P(n)\) debe ser una declaración, una oración matemática completa).
- Para obtener algo de práctica con el trabajo con\(P(n)\), use su respuesta en la parte (a) para escribir las declaraciones\(P(2)\) y\(P(5)\). (Haga un trabajo minucioso, asegúrese de escribir las declaraciones completas).
- Ahora para la Parte 4 de la lista: Escribe la declaración\(P(n_0)\) usando tu respuesta de la parte (a), y luego prueba que\(P(n_0)\) es verdad.
- Llevar a cabo la Parte 5: Escriba cuidadosamente la hipótesis de inducción que utilizaríamos en una prueba de inducción del enunciado anterior, comenzando con la palabra “Asumir”.
- ¿Cuál es el “objetivo” de la Parte 6? En otras palabras, ¿cuál es la afirmación específica sobre números y cuadrados perfectos que nos gustaría mostrar sostiene en esta parte?
- Sí o no, ¿te resulta fácil ver cómo usar los hechos\[\begin{aligned} 0 &= 0^2 + 0^2 + 0^2 + 0^2;& 3 &= 1^2 + 1^2 + 1^2 + 0^2;\\ 1 &= 1^2 + 0^2 + 0^2 + 0^2;& 4 &= 1^2 + 1^2 + 1^2 + 1^2;\\ 2 &= 1^2 + 1^2 + 0^2 + 0^2;& &\end{aligned}\] para escribir 5 como una suma de cuatro cuadrados perfectos? ¿Ves cómo completar la Parte 6 de las ocho partes principales, para alguna\(k\)? ¿Qué tan probable cree que es posible una prueba de inducción para la declaración con la que comenzamos? \(^{5}\)
\(2^n>6n\)Demuéstralo para\(n\geq 5\).
\(1+2+\cdots +n=\dfrac{n(n+1)}2\)Demuéstralo para\(n\geq 1\).
Utilizando sólo el PMI y las propiedades de las desigualdades del capítulo anterior, demostrar que si\(0 < a < b\) entonces\(0 < a^n<b^n\) para todos\(n \in \mathbb{N}\).
\(n!<n^n\)Demuéstralo para\(n\geq 2\).
(Para enteros positivos\(n\), definimos\(n\) factorial, escrito\(n!\), como el producto de todos los enteros entre e incluyendo\(n\) y\(1\). Por ejemplo,\(1! = 1\) y\(2! = 2\cdot 1 = 2\) y\(5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\).)
\(1+2+2^2+\cdots +2^n=2^{n+1}-1\)Demuéstralo para\(n \ge 1\).
Use PMI para probarlo\(\underbrace{111\cdots 1}_{n \,1\mbox {'s}}=\dfrac{10^n-1}9\) para\(n \ge 1\).
Demostrar que si\(a\) y\(r\) son números reales y\(r\neq 1\), entonces para\(n \ge 1\),\[a+ar+ar^2+\cdots +ar^n=\dfrac{a\left( r^{n+1}-1\right)}{r-1}.\nonumber \]
Demostrar que\(1^3+2^3+3^3+\cdots +n^3=\dfrac{n^2(n+1)^2}4\) si\(n\geq 1\). (Compare este resultado con Ejercicio\(\PageIndex{3}\).)
\(\dfrac{1}{1\cdot 2} + \dfrac{1}{2\cdot 3} + \dfrac{1}{3\cdot 4} + \cdots + \dfrac{1}{n(n+1)} = \dfrac{n}{n+1}\)Demuéstralo para todos\(n \geq 1\).
Quizás imitando los pasos de la “breve exploración” en este capítulo, conjetura una fórmula para cada una de las sumas a continuación. Luego usando PMI, demuestre que su fórmula conjeturada es correcta.
- \(1\cdot 2 + 2 \cdot 3 + 3 \cdot 4 + \cdots + n(n+1)\);
- \(1 + 3 + 5 + \cdots + (2n-1)\).
Usando inducción, probarlo\[a^n - b^n = (a-b)(a^{n-1}+a^{n-2}b + \cdots + ab^{n-2}+b^{n-1})\nonumber \] para todos los enteros\(n \geq 2\). (Pista: durante el paso de inducción, escriba\(a^{k+1}-b^{k+1} = a^{k+1}-ab^k + ab^k-b^{k+1}\).)
Demostrar que si\(n\geq 12\) entonces se\(n\) puede escribir como una suma de\(4\)\(5\)'s y 's. por ejemplo,\(23=5+5+5+4+4=3 \cdot 5+2 \cdot 4\).
(Pista: En este caso ayudará a hacer los casos\(n=12\),,\(13\)\(14\), y\(15\) por separado. Luego usa inducción para manejar\(n\geq 16\).)
- For\(n\ge 1\), el número triangular\(t_n\) es el número de puntos en una matriz triangular que tiene\(n\) filas con\(i\) puntos en la fila\(i\) -ésima. Encuentra una fórmula para\(t_n\),\(n\ge 1\).
- Supongamos que for\(n \geq 1\),\(s_n\) denota el número de puntos en una matriz cuadrada que tiene\(n\) filas con\(n\) puntos en cada fila. Encuentra una fórmula para\(s_n\). Los números\(s_n\) suelen llamarse cuadrados.
- Encuentra los primeros 10 números triangulares y los primeros 10 cuadrados.
- ¿Cuáles de los números triangulares de la parte (a) son también cuadrados?
- ¿Puedes encontrar el siguiente número triangular que es un cuadrado?
- Después de completar las partes (a) — (c), lee el artículo de Wikipedia.org “Número triangular cuadrado” y escribe una o más frases detalladas sobre lo que pensaste de él.
Algunas proposiciones que pueden probarse por inducción también se pueden probar sin inducción. Demostrar las proposiciones en Ejercicios\(\PageIndex{3}\) \(\PageIndex{8}\)y y \(\PageIndex{11}\)(b) sin inducción.
(Consejos: Para el ejercicio\(\PageIndex{3}\) escribir\(s=1+2+\dots+(n-1)+n\). Directamente bajo esta ecuación escribir\(s=n+(n-1)+\dots+2+1\). Sumar estas ecuaciones para obtener\(2s = n(n+1)\). Resolver para\(s\). Para Ejercicio\(\PageIndex{8}\) escribir\(p=a+ar+ar^2+\dots+ar^n\). Después multiplica ambos lados de esta ecuación por\(r\) para obtener una nueva ecuación con\(rp\) como el lado izquierdo. Restar estas dos ecuaciones para obtener\(pr-p=ar^{n+1}-a\). Ahora resuelve para\(p\). Para el Ejercicio\(\PageIndex{11}\) (b), dibuje filas de puntos como en el Ejercicio\(\PageIndex{14}\) (b) y divídalas en conjuntos de tamaño\(1,3,5,\dots\).
Notas al pie
[1] Aquí confiamos un poco en sus conocimientos previos. Discutiremos primos y factorizaciones de primos con más profundidad más adelante. Tenga en cuenta que no\(1\) es un primo.
[2] En otros cursos de matemáticas puede haber visto este principio llamado inducción fuerte, con inducción “ordinaria” refiriéndose a un principio con una condición (b) diferente a la que aparece aquí. Esto no debería importar demasiado; el PMI utilizado aquí se elige por simplicidad.
[3] Un ejemplo se puede encontrar\(\PageIndex{1}\) en Ejercicio al final del capítulo.
[4] Dependiendo de los detalles del PMI (b), a veces en PMI (a) no sólo\(P(n_0)\) sino también algunas declaraciones más específicas\(P(i)\) (tales como\(P(n_0 +1)\) o\(P(n_0 +2))\) son necesarias para verificar para que la lógica funcione; ver, por ejemplo, Ejercicio\(\PageIndex{13}\) al final del capítulo. La mayoría de las pruebas de inducción en este texto requerirán solo verificar\(P(n_0)\); cuando se requieran casos más tempranos, esto se señalará.
[5] Dejamos como pregunta sin respuesta si la afirmación en la que se basa este ejercicio es cierta, aunque volveremos a esta cuestión más adelante en el texto. El objetivo del ejercicio es demostrar que puedes llevar a cabo la mayor parte de las ocho partes principales incluso antes de que descubras cómo llevar a cabo la Parte 6 (¡o incluso antes de que sepas si la afirmación que estás intentando probar es incluso cierta!).


