7.4: Pedidos parciales y totales

Dos relaciones especiales ocurren frecuentemente en matemáticas. Ambos tienen que ver con algún tipo de ordenación de los elementos en un conjunto. Una rama de las matemáticas se dedica a su estudio. Como se puede apreciar de la breve discusión en esta sección, cubren muchos conceptos familiares.

Una relación en un conjunto no vacío\(A\) se denomina relación de orden parcial o de orden parcial si es reflexiva, antisimétrica y transitiva. A menudo usamos\(\preceq\) para denotar un orden parcial, y se llama\((A,\preceq)\) un conjunto parcialmente ordenado o un poset.

Ejemplo\(\PageIndex{1}\label{eg:ordering-01}\)

La relación habitual de “menor o igual a” sobre\(R\), denotada\(\leq\), es un ejemplo perfecto de ordenamiento parcial. De hecho, esta es la razón por la que adoptamos la notación\(\preceq\), ya que refleja las similitudes entre los dos símbolos.

Ejemplo\(\PageIndex{2}\label{eg:ordering-02}\)

Otro ejemplo clásico de ordenación parcial es la relación de subconjunto, denotada\(\subseteq\), on\(\wp(S)\), donde\(S\) está cualquier conjunto de elementos. Observe que\(S\) puede estar vacío, en cuyo caso\(\wp(\emptyset) = \{\emptyset\}\), y\((\wp(\emptyset),\subseteq)\) es obviamente un conjunto parcialmente ordenado.

Ejemplo\(\PageIndex{3}\label{eg:ordering-03}\)

Otro ejemplo estándar de poset es\((\mathbb{N},\mid)\). Es fácil verificar que la relación “divide” sobre los números naturales es un orden parcial. ¿Puedes explicar por qué no\((\mathbb{Z}^*,\mid)\) es un poset?

Ejercicio\(\PageIndex{1}\label{he:ordering-01}\)

Encuentra un contraejemplo para ilustrar por qué la relación “divide”, denotada\(\mid\), sobre no\(\mathbb{Z}^*\) es antisimétrica. ¿La relación “divide” es reflexiva\(\mathbb{Z}\)? ¿Qué tal la transitividad?

Ejercicio\(\PageIndex{2}\label{he:ordering-02}\)

Definir la relación\(\sqsubseteq\) de\(\wp(\{a,b,c,d\})\) acuerdo con\[S\sqsubseteq T \,\Leftrightarrow\, S\subseteq T\cup\{a\}. \nonumber\] ¿Es\((\wp(\{a,b,c,d\},\sqsubseteq)\) un poset? ¿Qué propiedades no posee? Explique.

Obviamente, si\(a\preceq b\) pero\(a\neq b\), entonces podemos escribir\(a \prec b\). A veces decimos que\(a\) precede\(b\), o\(b\) tiene éxito\(a\). También decimos que\(a\) es el predecesor de\(b\), o\(b\) es el sucesor de\(a\).

El dígrafo para un poset se puede simplificar. Dado que siempre\(a\) está relacionado\(a\) consigo mismo, es redundante dibujar un bucle alrededor de cada vértice. Desde\(a\preceq b\) y\(b\preceq c\) siempre implica eso\(a\preceq c\), no hay necesidad de incluir el arco (borde dirigido) de\(a\) a\(c\). Entonces seguimos la convención de que sólo dibujamos un arco de\(a\) a\(b\) si\(a\prec b\) y no existe otro elemento\(t\) tal que\(a\prec t\) y\(t\prec b\). Por último, si\(a\prec b\), podemos colocar\(b\) arriba\(a\) para que todos los arcos estén apuntando hacia arriba. Esto sugiere que podemos usar líneas no dirigidas para facilitar la lectura de la gráfica. Todas estas modificaciones conducen a una representación gráfica mucho más simple llamada diagrama de Hasse.

Ejemplo\(\PageIndex{4}\label{eg:ordering-04}\)

Es claro que\((\{1,2,3,4,6,12\},\mid)\) es un poset. Su diagrama de Hasse se muestra a continuación.

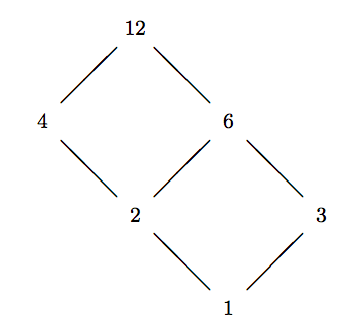
En esta convención de usar línea no dirigida, la\(\preceq\) relación (de ahí, el orden de los elementos) se lee de abajo hacia arriba.

Ejercicio\(\PageIndex{3}\label{he:ordering-03}\)

Dibuja el diagrama de Hasse para el poset\((\{1,2,3,4,6,9,12,18,36\},\mid)\).

La definición de un poset no requiere que cada par de elementos distintos sea comparable. Esto significa que puede existir\(a\neq b\) tal que\(a\not\preceq b\) y\(b\not\preceq a\). Un ejemplo se puede encontrar en los números 2 y 3 del Ejemplo 7.4.4. Si un ordenamiento parcial tiene la propiedad adicional que para dos elementos distintos cualesquiera\(a\) y\(b\), cualquiera\(a\prec b\) o\(b\prec a\) (por lo tanto, cualquier par de elementos distintos son comparables), llamamos a la relación un ordenamiento total.

Ejemplo\(\PageIndex{5}\label{eg:ordering-05}\)

El poset\((\mathbb{N},\leq)\) es un conjunto totalmente ordenado. El poset también\((\{1,5,25,125\},\mid)\) es un conjunto totalmente ordenado. Su diagrama de Hasse se muestra a continuación.

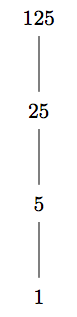
Está claro que el diagrama de Hasse de cualquier conjunto totalmente ordenado se verá como el que se muestra arriba. En consecuencia, un orden total también se denomina ordenamiento lineal. Un conjunto totalmente ordenado también se llama cadena.

Ejercicio\(\PageIndex{4}\label{he:ordering-04}\)

Construye el diagrama de Hasse para el poset\((\{1,2,4,18,16\},\mid)\). ¿Es un conjunto totalmente ordenado?

Ejercicio\(\PageIndex{5}\label{he:ordering-05}\)

Construye el diagrama de Hasse para el poset\((\wp(\{a,b,c\}),\subseteq)\).

Resumen y revisión

• Una relación reflexiva, antisimétrica y transitiva se denomina ordenamiento parcial.
• Un conjunto con un orden parcial se llama conjunto parcialmente ordenado o poset.
• Un poset con cada par de elementos distintos comparables se llama un conjunto totalmente ordenado.
• Un orden total también se llama orden lineal, y un conjunto totalmente ordenado también se llama cadena.

Ejercicio\(\PageIndex{1}\label{ex:ordering-01}\)

Dejar\(A\) ser el conjunto de números naturales que son divisores de 30. Construye el diagrama de Hasse de\((A,\mid)\).

Ejercicio\(\PageIndex{2}\label{ex:ordering-02}\)

Vamos\(S = \big\{\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\}\big\}\). Construya el diagrama de Hasse para\((S,\subseteq)\).

Ejercicio\(\PageIndex{3}\label{ex:ordering-03}\)

Dejar\((A,\preceq)\) ser un poset, y\(B\) un subconjunto no vacío de\(A\). Demostrar que también\((B,\preceq)\) es un poset. Naturalmente, llamamos\((B,\preceq)\) una citación de\((A,\preceq)\).

Ejercicio\(\PageIndex{4}\label{ex:ordering-04}\)

Definir la relación\(\preceq\) de\(\mathbb{Z}\) acuerdo con\[a\preceq b \,\Leftrightarrow\, a=b \mbox{ or } a\bmod3 < b\bmod3. \nonumber\]

• Demostrar que\((\mathbb{Z},\preceq)\) es un poset.
• Vamos\(B=\{-3,-2,-1,0,1,2,-3\}\). Construya el diagrama de Hasse para el citatorio\((B,\preceq)\).

Ejercicio\(\PageIndex{5}\label{ex:ordering-05}\)

Definir la relación\(\preceq\) de\(\mathbb{Z}\) acuerdo con\[a\preceq b \,\Leftrightarrow\, a=b \mbox{ or } |a|<|b|. \nonumber\]

• Demostrar que\((\mathbb{Z},\preceq)\) es un poset.
• Construya el diagrama de Hasse para el citatorio\((B,\preceq)\), donde\(B=\{-2,-1,0,1,2\}\).

Ejercicio\(\PageIndex{6}\label{ex:ordering-06}\)

Definir la relación\(\preceq\) de\(\mathbb{Z}\times\mathbb{Z}\) acuerdo con\[(a,b)\preceq(c,d) \,\Leftrightarrow\, (a,b)=(c,d) \mbox{ or } a^2+b^2<c^2+d^2. \nonumber\]

• Demostrar que\((\mathbb{Z}\times\mathbb{Z},\preceq)\) es un poset.
• Construya el diagrama de Hasse para el citatorio\((B,\preceq)\), donde\(B=\{0,1,2\}\times\{0,1,2\}\).

Ejercicio\(\PageIndex{7}\label{ex:ordering-07}\)

Construir un ejemplo de un subconjunto\(B\) de\(\wp(\{a,b,c,d\})\) tales que\((B,\subseteq)\) sea un conjunto totalmente ordenado.

Ejercicio\(\PageIndex{8}\label{ex:ordering-08}\)

Dejar\[A = \{(m,n)\mid m,n\in\mathbb{N} \mbox{ and } \gcd(m,n)=1\}, \nonumber\] y definir la relación\(\preceq\) de\(A\) acuerdo a\[(a,b)\preceq(c,d) \,\Leftrightarrow\, ad\leq bc. \nonumber\] Demostrar que\((A,\preceq)\) es un conjunto totalmente ordenado.