1.3: Distribución de Primes

Última actualización
Guardar como PDF

Page ID: 113187

Leo Moser
University of Alberta via The Trilla Group

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Quizás la prueba más conocida en todas las matemáticas “reales” es la prueba de Euclides de la existencia de infinitamente muchos primos.

Teorema$\PageIndex{1}$: existence of infinitely many primes

Si$p$ fuera el prime más grande entonces no$(2 \cdot 3 \cdot 5 \cdot\cdot\cdot p) + 1$ sería divisible por ninguno de los primos hasta$p$ y por lo tanto sería el producto de primos superiores$p$

A pesar de su extrema simplicidad esta prueba ya plantea muchas preguntas sumamente difíciles, por ejemplo, ¿los números$(2 \cdot 3 \cdot ... \cdot p) + 1$ suelen ser primos o compuestos? No se conocen resultados generales. De hecho, no sabemos si una infinidad de estos números son primos, o si un infinito son compuestos.

La prueba puede ser variada de muchas maneras. Por lo tanto, podríamos considerar$(2 \cdot 3 \cdot 5 \cdot\cdot\cdot p) - 1$ o$p! + 1$ o$p! - 1$. Nuevamente casi no se sabe nada de cómo factores tales números. Los dos últimos conjuntos de números traen a la mente un problema que revela cómo, en teoría de números, lo trivial puede estar muy cerca de lo más abstracto. Es bastante trivial que para no$n > 2, n! - 1$ sea un cuadrado perfecto. ¿De qué se puede decir$n! + 1$? Bueno,$4! + 1 = 5^2$,$5! + 1 = 11^2$ y$7! + 1 = 71^2$. Sin embargo, no se conocen otros casos; ni se sabe si otros números$n! + 1$ son cuadrados perfectos. Volveremos a este problema en las conferencias sobre ecuaciones diofantinas.

Después de Euclides, el siguiente avance sustancial en la teoría de la distribución de primos fue realizado por Euler. Demostró que$\sum \dfrac{1}{p}$ diverge, y describió este resultado diciendo que los primos son más numerosos que los cuadrados. Quisiera presentar ahora una nueva prueba de este hecho —una prueba que está algo relacionada con la prueba de Euclides de la existencia de infinitamente muchos primos.

Primero necesitamos un lema (bien conocido) relativo a las subseries de la serie armónica. Dejar$p_1 < p_2 < ...$ ser una secuencia de enteros positivos y dejar que su función de conteo sea

\[\pi (x) = \sum_{p \le x} 1.\]

Let

\[R(x) = \sum_{p \le x} \dfrac{1}{p}.\]

Lema

Si$R(\infty)$ existe entonces

\[\lim_{x \to \infty} \dfrac{\pi(x)}{x} = 0.\]

Prueba

\[\pi(x) = 1 (R(1) - R(0)) + 2 ((R(2) - R(1)) + ... + x(R(x) - R(x - 1))\]

\[\dfrac{\pi (x)}{x} = R(x) - \left[\dfrac{R(0) + R(1) + \cdot\cdot\cdot R(x - 1)}{x}\right].\]

Dado que$R(x)$ se acerca a un límite, la expresión entre corchetes se acerca a este límite y se prueba el lema.

En lo que sigue suponemos que los$p$'s son los primos.

Para probar que$\sum \dfrac{1}{p}$ diverge asumiremos lo contrario, es decir,$\sum \dfrac{1}{p}$ converge (y de ahí también eso$\dfrac{\pi(x)}{x} \to 0$) y derivaremos una contradicción.

\[\sum_{p > n} \dfrac{1}{p} < \dfrac{1}{2}.\]

Pero ahora esto$n$ está arreglado así que también habrá$m$ tal que

\[\dfrac{\pi (n!m)}{n!m} < \dfrac{1}{2n!}.\]

Con tal$n$ y$m$ formamos los$m$ números

$T_1 = n! - 1, T_2 = 2n! - 1, ..., T_m = mn! - 1.$

Tenga en cuenta que ninguno de los$T$'s tiene factores primos$\le n$ o$\ge mn!$. Además si$p | T_i$ y$p | T_j$$p | (T_i - T_j)$ entonces para eso$p | (i - j)$. En otras palabras, los múltiplos de$p$ están$p$ separados en nuestro conjunto de números. De ahí que no más$\dfrac{m}{p} + 1$ de los números sean divisibles por$p$. Como cada número tiene al menos un factor primo tenemos

$\sum_{n < p < n! m} (\dfrac{m}{p} + 1) \ge m$

$\sum_{n< p} \dfrac{1}{p} + \dfrac{\pi (n!m)}{m} \ge 1.$

Pero ahora por (1) y (2) el lado derecho debería ser < 1 y tenemos una contradicción, lo que prueba nuestro teorema.

La prueba de Euler, que es más significativa, depende de su identidad muy importante

$\zeta (s) = \sum_{n = 1}^{\infty} \dfrac{1}{n^s} = \prod_{p} \dfrac{1}{1 - \dfrac{1}{p^s}}.$

Esta identidad es esencialmente una declaración analítica del teorema de factorización único. Formalmente, su validez se puede ver fácilmente. Tenemos

$\begin{array} {rcl} {\prod_{p} \dfrac{1}{1 - \dfrac{1}{p^s}}} & = & {\prod_p (1 + \dfrac{1}{p^s} + \dfrac{1}{p^{2s}} + \cdot\cdot\cdot)} \\ {} & = & {(1 + \dfrac{1}{2^s} + \cdot\cdot\cdot)(1 + \dfrac{1}{3^s} + \cdot\cdot\cdot)(1 + \dfrac{1}{5^s} + \cdot\cdot\cdot)} \\ {} & = & {\dfrac{1}{1^s} + \dfrac{1}{2^s} + \dfrac{1}{3^s} + \cdot\cdot\cdot.} \end{array}$

Euler ahora argumentó que para$s = 1$,

$\sum_{n = 1}^{\infty} \dfrac{1}{n^s} = \infty$

para que

$\prod_p \dfrac{1}{1 - \dfrac{1}{p}}$

debe ser infinito, lo que a su vez implica que eso$\sum \dfrac{1}{p}$ debe ser infinito.

Este argumento, aunque no del todo válido, ciertamente puede hacerse válido. De hecho, se puede demostrar sin mucha dificultad que

$\sum_{n \le x} \dfrac{1}{n} - \prod_{p \le x} (1 - \dfrac{1}{p})^{-1}$

está acotado. Dado que$\sum_{n \le x} \dfrac{1}{n} - \text{log} x$ está acotado, podemos, al tomar registros, obtener

$\text{loglog} x = \sum_{p \le x} - \text{log} (1 - \dfrac{1}{p}) + O(1)$

para que

$\sum_{p \le x} \dfrac{1}{p} = \text{loglog} x + O(1).$

Utilizaremos este resultado más adelante.

Gauss y Legendre fueron los primeros en hacer estimaciones razonables para$\pi (x)$. Esencialmente, conjeturaron que

$\pi(x) \thicksim \dfrac{x}{\text{log} x},$

el famoso Teorema de los Números Primos. Si bien esto fue probado en 1896 por J. Hadamard y de la Vallee Poussin, el primer avance sustancial hacia este resultado se debe a Chebycheff. Obtuvo los siguientes tres resultados principales:

Hay un primo entre$n$ y$2n$ ($n > 1$);
Existen constantes positivas$c_1$ y$c_2$ tales que\[\dfrac{c_2 x}{\text{log} x} < \pi (x) < \dfrac{c_1 x}{\text{log} x};\]
Si$\dfrac{\pi (x)}{\text{log} x}$ se acerca a un límite, entonces ese límite es 1.

Demostraremos los tres resultados principales de Chebycheff utilizando sus métodos modificados por Landau, Erd$\ddot{\text{o}}$ s y, en menor medida, L. Moser.

Requerimos de una serie de lemmas. El primero de ellos se relaciona con la magnitud de

$n!$y${2n \choose n}$.

En lo que$n!$ se refiere, podríamos usar la aproximación de Stirling

$n! \thicksim n^n e^{-n} \sqrt{2 \pi n}.$

No obstante, para nuestros fines bastará con una estimación más simple. Desde

$\dfrac{n^n}{n!}$

y tenemos el siguiente lema.

Lema 1

$n^n e^{-n} < n! < n^n$.

Prueba

Desde

$(1 + 1)^{2n} = 1 + {2n \choose 1} + \cdot\cdot\cdot + {2n \choose n} + \cdot\cdot\cdot + 1,$

se deduce que

${2n \choose n} < 2^{2n} = 4^n.$

Esta estimación para no${2n \choose n}$ es tan cruda como parece, pues se puede ver fácilmente a partir de la fórmula de Stirling que

${2n \choose n} \thicksim \dfrac{4^n}{\sqrt{\pi n}}.$

Usando inducción podemos mostrar para$n > 1$ eso

${2n \choose n} > \dfrac{4^n}{2n},$

y así tenemos

lema 2

$\dfrac{4^n}{2n} < {2n \choose n} < 4^n.$

Prueba: Tenga en cuenta que${2n + 1 \choose n}$ es uno de dos términos iguales en la expansión de$(1 + 1)^{2n + 1}$. De ahí que también tenemos

LeMMA 3

${2n + 1 \choose n} < 4^n.$

Prueba

Como ejercicio podrías usar estos para demostrar que si

$n = a + b + c + \cdot\cdot\cdot$

entonces

$\dfrac{n!}{a! b! c! \cdot\cdot\cdot} < \dfrac{n^n}{a^ab^bc^c \cdot\cdot\cdot}.$

Ahora deducimos información sobre cómo$n!$ y${2n \choose n}$ factorizamos como producto de los primos. Supongamos que$e_p (n) is the exponent of the prime \(p$ en la factorización de potencia principal de$n!$, i.e.

$n! = \prod p^{e_p (n)}.$

Demostramos fácilmente

lema 4

(Legendre). $e_p (n) = [\dfrac{n}{p}] + [\dfrac{n}{p^2}] + [\dfrac{n}{p^3}] + \cdot \cdot\cdot.$

Prueba

De hecho$[\dfrac{n}{p}]$ es el número de múltiplos de$p$ in$n!$, el término$[\dfrac{n}{p^2}]$ suma la contribución adicional de los múltiplos de$p^2$, y así sucesivamente, e.g.

$e_3(30) = [\dfrac{30}{3}] + [\dfrac{30}{9}] + [\dfrac{30}{27}] + \cdot\cdot\cdot = 10 + 3 + 1 = 14.$

Una expresión alternativa interesante y a veces útil para$e_p (n)$ la da

$e_p(n) = \dfrac{n - s_p (n)}{p - 1}, $

donde$s_p (n)$ representa la suma de los dígitos de$n$ cuando$n$ se expresa en base$p$. Así en base 3, 30 se puede escribir 1010 para que$e_3(30) = \dfrac{30 - 2}{2} = 14$ como antes. Dejamos como ejercicio el comprobante del caso general.

A continuación consideramos la composición de${2n \choose n}$ como producto de primos. Dejar$E_p(n)$ denotar el exponente de$p$ in${2n \choose n}$, es decir,

${2n \choose n} = \prod_p p^{E_p(n)}.$

Claramente

$E_p (n) = e_p (2n) - 2 e_p (n) = \sum_i {[\dfrac{2n}{p^i}] - 2\ [\dfrac{n}{p^i}]}.$

Nuestra expresión alternativa para$e_p(n)$ rendimientos

$E_p(n) = \dfrac{2s_p(n) - s_p(2n)}{p - 1}.$

En la primera expresión cada término en la suma se puede ver fácilmente como 0 o 1 y el número de términos no excede el exponente de la potencia más alta de$p$ que no exceda$2n$. De ahí

lema 5

$E_p(n) \le \text{log}_p (2n).$

lema 6

La contribución de$p$ a${2n \choose n}$ no excede$2n$

Los siguientes tres lemmas son inmediatos.

lema 7

Cada primo en el rango$n < p < 2n$ aparece exactamente una vez en${2n \choose n}$

lema 8

Ningún primo en el rango$p > \sqrt{2n}$ aparece más de una vez en${2n \choose n}$

A pesar de que no es necesario en lo que sigue, es divertido notar que desde$E_2(n) = 2s_2 (n) - s_2 (2n)$ y$s_2(n) = s_2 (2n)$, tenemos$E_2(n) = s_2(n)$.

Como primera aplicación de los lemmas demostramos el resultado elegante

Teorema 1

$\prod_{p \le n} p < 4^n$.

Prueba

La prueba es por inducción en$n$. Asumimos el teorema verdadero para los enteros$< n$ y consideramos los casos$n = 2m$ y$n = 2m + 1$. Si$n = 2m$ entonces

$\prod_{p \le 2m} p = \prod_{p \le 2m - 1} p < 4^{2m - 1}$

por la hipótesis de inducción. Si$n = 2m + 1$ entonces

$\begin{array} {rcl} {\prod_{p \le 2m + 1} p} & = & {(\prod_{p \le m + 1} p)(\prod_{m + 1 < p < 2m + 1} p)} \\ {} & < & {4^{m + 1} {2m + 1 \choose m} \le 4^{m + 1} 4^m = 4^{2m + 1}} \end{array}$

y la inducción es completa.

Se puede demostrar por métodos mucho más profundos (Rosser) que

$\prod_{p \le n} p < (2.83)^n.$

En realidad, el teorema del número primo es equivalente a

$\sum_{p \le n} \text{log } p \thicksim n.$

Del Teorema 1 podemos deducir

Teorema 2

$\pi (n) < \dfrac{cn}{\text{log} n}. $

Prueba

Claramente

$4^n > \prod_{p \le n} p > \prod_{\sqrt{n} \le p \le n} p > \sqrt{n} ^{\pi (n) - \pi (\sqrt{n})}$

Tomando logaritmos obtenemos

\ (n\ texto {registro} 4 > (\ pi (n) -\ pi (\ sqrt {n}))\ dfrac {1} {2}\ texto {log} n)

$\pi(n) - \pi(\sqrt{n}) < \dfrac{n \cdot 4 \text{log } 2}{\text{log } n}$

$\pi (n) < (4 \text{log } 2) \dfrac{n}{\text{log } n} + \sqrt{n} < \dfrac{cn}{\text{log } n}$.

A continuación probamos

Teorema 3

$\pi(n) > \dfrac{cn}{\text{log} n}$.

Prueba

Para ello utilizamos Lemmas 6 y 2. De estos obtenemos

$(2n)^{\pi(2n)} > {2n \choose n} > \dfrac{4^n}{2n}.$

Tomando logaritmos, encontramos que

$(\pi (n) + 1) \text{log } 2n > \text{log } (2^{2n}) = 2n \text{log } 2.$

Por lo tanto, para incluso$m$

$\pi(m) + 1 > \dfrac{m}{\text{log } m} \text{log } 2$

y el resultado sigue.

A continuación obtenemos un extimate para$S(x) = \sum_{p \le x} \dfrac{\text{log }p}{p}.$ tomar el logaritmo de$n! = \prod_p p^{e_p}$ encontramos que

$n \text{log } n > \text{log } n! = \sum e_p (n) \text{log } p > n (\text{log } n - 1).$

El lector puede justificar que el error introducido en la sustitución$e_p(n)$ por$\dfrac{n}{p}$ (por supuesto$e_p(n) = \sum [\dfrac{n}{p^i}]$) es lo suficientemente pequeño como para

$\sum_{p \le n} \dfrac{n}{p} \text{log } p = n \text{log } n + O(n)$

$\sum_{p \le n} \dfrac{\text{log }p}{p} = \text{log } n + O(1)$.

Ahora podemos probar

Teorema 4

$R(x) = \sum_{p \le x} \dfrac{1}{p} = \text{log log } x + O(1)$.

Prueba

De hecho

$\begin{array} {rcl} {R(x)} & = & {\sum_{n = 2}^{x} \dfrac{S(n) - S(n - 1)}{\text{log } n}} \\ {} & = & {\sum_{n = 2}^{x}S(n) (\dfrac{1}{\text{log } n} - \dfrac{1}{\text{log }(n + 1)}) + O(1)} \\ {} & = & {\sum_{n = 2}^{x} (\text{log } n + O(1)) \dfrac{\text{log }(1 + \dfrac{1}{n}}{(\text{log } n) \text{log } (n + 1)} + O(1)} \\ {} & = & {\sum_{n = 2}^{x} \dfrac{1}{n \text{log } n} + O(1)} \\ {} & = & {\text{log log } x + O(1)} \end{array}$

según se desee.

Ahora esbozamos la prueba de Chebycheff

Teorema 5

Si$\pi(x) \thicksim \dfrac{cx}{\text{log }x}$, entonces$c = 1$.

Prueba

Desde

$\begin{array} {rcl} {R(x)} &= & {\sum_{n = 1}^{x} \dfrac{\pi(n) - \pi(n - 1)}{n}} \\ {} &= & {\sum_{n = 1}^{x} \dfrac{\pi(n)}{n^2} + O(1)} \end{array}$

$\pi(x) \thicksim \dfrac{cx}{\text{log }x}$implicaría

$\sum_{n = 1}^{x} \dfrac{\pi(n)}{n^2} \thicksim c\text{log log }x$.

Pero ya lo sabemos$\pi(x) \thicksim \text{log log } x$ por lo que se deduce de eso$c = 1$.

A continuación damos una prueba del Postulado de Bertrand desarrollado hace unos diez años (L. Moser). Para que la prueba vaya más suavemente solo demostramos el algo más débil

Teorema 6: Postulado de Bertrand

Por cada entero$r$ existe un primo$p$ con

$3 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r}$.

Reafirmamos varios de nuestros lemmas en la forma en que serán utilizados.

Si$n < p < 2n$ entonces$p$ ocurre exactamente una vez adentro${2n \choose n}$.
Si$2 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r - 1}$ entonces$p$ no ocurre en${3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}$.
Si$p > 2^{r + 1}$ entonces$p$ ocurre a lo sumo una vez en${3 \cdot 2^{2n} \choose 3 \cdot 2^{2n - 1}}$.
Ningún primo ocurre más de$2r + 1$ veces en${3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}$

Ahora comparamos${3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}$ y

${2^{2r} \choose 2^{2r - 1}} {2^{2r - 1} \choose 2^{2r - 2}} \cdot \cdot \cdot {2 \choose 1} {{2^{r + 1} \choose 2^r}{2^r \choose 2^{r - 1}} \cdot\cdot\cdot {2 \choose 1} }^{2r}.$

Supongamos que no hay primo en el rango$3 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r}$. Entonces, por nuestros lemas, encontramos que cada primo que ocurre en la primera expresión también ocurre en la segunda con al menos una multiplicidad tan alta; es decir, la segunda expresión no es menor que la primera. Por otro lado, observando que para$r \ge 6$

$3 \cdot 2^{2r} > (2^{2r} + 2^{2r - 1} + \cdot\cdot\cdot + 2) + 2r(2^{r + 1} + 2r + \cdot\cdot\cdot + 2),$

e interpretando${2n \choose n}$ como el número de formas de elegir$n$ objetos$2n$, concluimos que la segunda expresión es efectivamente menor que la primera. Esta contradicción prueba el teorema cuando$r > 6.$ Los primos 7, 29, 97, 389 y 1543 muestran que el teorema también es cierto para$r \le 6$.

La prueba del Postulado de Bertrand por este método se deja como ejercicio.

El Postulado de Bertrand podrá ser utilizado para probar los siguientes resultados.

(1) nunca$\dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}$ es un entero.

(2) Cada entero > 6 se puede escribir como la suma de primos distintos.

(3) Cada primo se$p_n$ puede expresar en la forma

$p_n = \pm 2 \pm 3 \pm 5 \pm \cdot\cdot\cdot \pm p_{n - 1}$

con un error de como máximo 1 (Scherk).

(4) La ecuación$\pi(n) = \varphi (n)$ tiene exactamente 8 soluciones.

Hacia 1949 una sensación fue creada por el descubrimiento por Erd os y Selberg de una prueba elemental del Teorema del Número Primo. El principal nuevo resultado fue la siguiente estimación, comprobada de manera elemental:

$\sum_{p \le x} \text{log}^2 p + \sum_{pq \le x} \text{log }p\text{log }q = 2x \text{log } x + O(x)$.

Si bien la desigualdad de Selberg aún está lejos del Teorema de los números primos, este último se puede deducir de él de diversas maneras sin recurrir a ningún otro resultado teórico numérico. Se han dado varias pruebas de este lema, quizá la más sencilla debido a Tatuzawa e Iseki. La prueba original de Selberg depende de la consideración de las funciones

$\lambda_n = \lambda_{n, x} = \sum_{d|n} \mu (d) \text{log}^2 \dfrac{x}{d}$

$T(x) = \sum_{n = 1}^{x} \lambda_n x^n$.

Hace unos cinco años J. Lambek y L. Moser demostraron que se podía probar el lema de Selberg de una manera completamente elemental, es decir, usando propiedades de inte- gers solamente. Una de las principales herramientas para hacer esto es el siguiente análogo racional de la función logaritmo. Let

$h(n) = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}$y$\ell_k(n) = h(kn) - h(k).$

Demostramos de una manera bastante elemental que

$|\ell_k (ab) - \ell_k (a) - \ell_k (b)| < \dfrac{1}{k}.$

Los resultados que hemos establecido son útiles en la investigación de la magnitud de las funciones aritméticas$\sigma_k(n)$,$\varphi_k(n)$ y$\omega_k(n)$. Dado que estos dependen no sólo de la magnitud de$n$ sino también fuertemente de la estructura aritmética de no$n$ podemos esperar aproximarlos por las funciones elementales del análisis. Sin embargo veremos que “en promedio” estas funciones tienen un comportamiento bastante simple.

Si$f$ y$g$ son funciones para las cuales

$f(1) + f(2) + \cdot\cdot\cdot + f(n) \thicksim g(1) + g(2) + \cdot\cdot\cdot g(n)$

decimos eso$f$ y$g$ tenemos el mismo orden promedio. Veremos, por ejemplo, que el orden promedio de$\tau(n)$ es log$n$, el de$\sigma(n)$ es$\dfrac{\pi ^2}{6} n$ y el de$\varphi (n)$ es$\dfrac{6}{\pi ^2} n$.

Consideremos primero un argumento puramente heurístico para obtener el valor promedio de$\sigma_k(n)$. La probabilidad que$r\ |\ n$ es$\dfrac{1}{r}$ y si$r\ |\ n$ entonces$\dfrac{n}{r}$ contribuye$(\dfrac{n}{r})^k$ a$\sigma_k (n)$. Así, el valor esperado de$\sigma_k (n)$ es

$\begin{array} {rcl} {\dfrac{1}{1} (\dfrac{n}{1})^k} & + & {\dfrac{1}{2} (\dfrac{n}{2})^k + \cdot\cdot\cdot + \dfrac{1}{n} (\dfrac{n}{n})^k} \\ {} & = & {n^k(\dfrac{1}{1^{k + 1}} + \dfrac{1}{2^{k + 1}} + \cdot\cdot\cdot + \dfrac{1}{n^{k + 1}})} \end{array}$

Para$k = 0$ esto será sobre$n \text{log } n$. Porque$n \ge 1$ será sobre$n^k \zeta (k + 1)$, e.g.,$n = 1$ porque será sobre$n \zeta(2) = n \dfrac{\pi ^2}{6}$.

Antes de proceder a la prueba y refinamiento de algunos de estos resultados consideramos algunas aplicaciones de la inversión del orden de suma en ciertas sumas dobles.

Dejar$f$ ser una función aritmética y asociar con ella la función

$F(n) = \sum_{d = 1}^{n} f(d)$

y$g = f \times I$, es decir,

$g(n) = \sum_{d|n} f(d).$

Obtendremos dos expresiones para

$\mathcal{F} (x) = \sum_{n = 1}^{x} g(n)$.

$\mathcal{F}(x)$es la suma

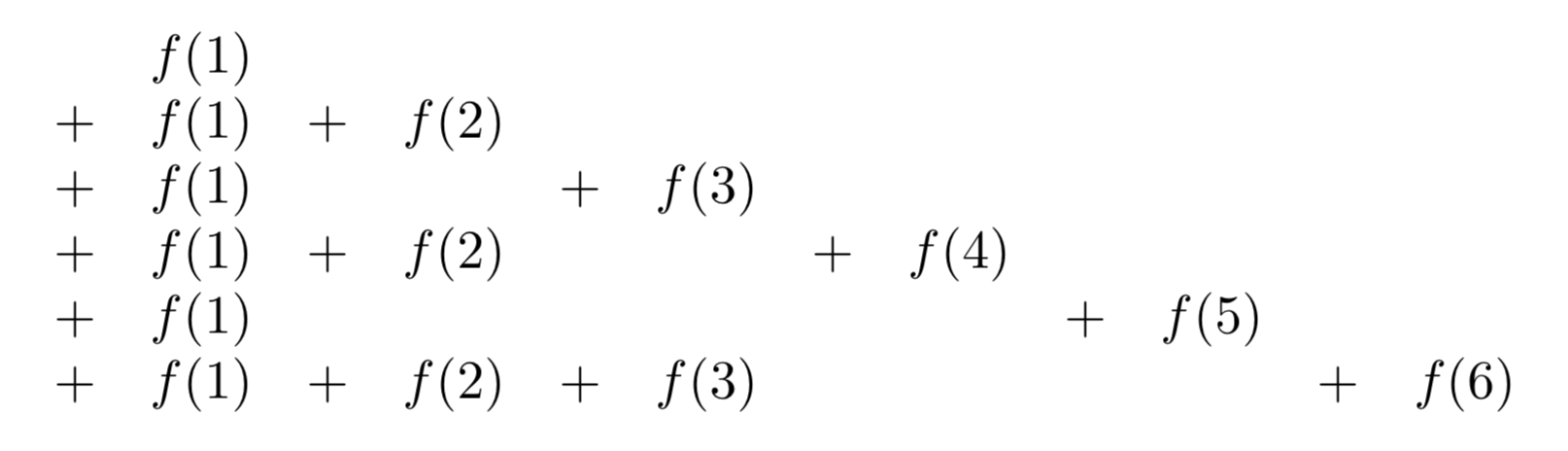
$2019-11-05 7.25.30.png$

Sumando a lo largo de líneas verticales tenemos

$\sum_{d = 1}^{x} [\dfrac{x}{d}] f(d)$;

si sumamos a lo largo de las sucesivas líneas diagonales cada una comenzando con$f(1)$ y con “pendientes” −1, −2, −3,.,., obtenemos

$\sum_{n = 1}^{x} F([\dfrac{x}{n}]).$

Por lo tanto

$\sum_{n = 1}^{x} \sum_{d|n} f(d) = \sum_{d = 1}^x [\dfrac{x}{d}] f(d) = \sum_{n = 1}^x F([\dfrac{x}{n}]).$

El caso especial$f = \mu$ rinde

$1 = \sum_{d = 1}^{x} \mu(d) [\dfrac{x}{d}] = \sum_{n = 1}^{x} M([\dfrac{x}{n}]),$

que antes considerábamos.

Desde

$\sum_{d = 1}^x \mu(d) [\dfrac{x}{d}] = 1$,

tenemos, al quitar los corchetes, permitiendo el error, y dividiendo por$x$,

$|\sum_{d = 1}^{x} \dfrac{\mu(d)}{d}| < 1$.

En realidad, se sabe que

$\sum_{d = 1}^{\infty} \dfrac{\mu(d)}{d} = 0$,

pero una prueba de ello es tan profunda como la del teorema del número primo.

A continuación consideramos el caso$f = 1$. Aquí obtenemos

$\sum_{n = 1}^{x} \tau(n) = \sum_{n = 1}^{x} [\dfrac{x}{n}] = x \log x+ O(x)$.

En el caso$f = I_k$ nos encontramos con que

$\sum_{n = 1}^{x} \sigma_k (n) = \sum_{d = 1}^{x} d^k [\dfrac{x}{d}] = \sum_{n = 1}^{x} (1^k + 2^k + \cdot\cdot\cdot + [\dfrac{x}{n}])$.

En el caso$f = \varphi$, recordando que$\sum_{d|n} \varphi (d) = n$, obtenemos

$\dfrac{x(x + 1)}{2} = \sum_{n = 1}^{x} \sum_{d |n} \varphi (d) = \sum_{d = 1}^{x} [\dfrac{x}{d}] \varphi (d) = \sum_{n = 1}^{x} \Phi (\dfrac{x}{n})$,

donde$\Phi (n) = \sum_{d = 1}^{n} \varphi (d)$. De esto obtenemos fácilmente

$\sum_{d = 1}^{x} \dfrac{\varphi (d)}{d} \ge \dfrac{x + 1}{2}$,

lo que revela que, en promedio,$\varphi (d) > \dfrac{d}{2}$.

También se puede utilizar una inversión similar del orden de suma para obtener la siguiente fórmula importante de inversión de M$\ddot{o}$ bius:

Teorema

Si$G(x) = \sum_{n = 1}^{x} F([\dfrac{x}{n}])$ entonces$F(x) = \sum_{n = 1}^{x} \mu(n) G([\dfrac{x}{n}]).$

Prueba: $\begin{array} {rcl} {\sum_{n = 1}^{x} \mu(n) G([\dfrac{x}{n}])} &= & {\sum_{n = 1}^{x} \mu(n) \sum_{n = 1}^{[x/n]} F([\dfrac{x}{mn}])} \\ {} & = & {\sum_{k = 1}^{x} F([\dfrac{x}{n}]) \sum_{n |k}^{x} \mu (n) = F(x).} \end{array}$

Considera de nuevo nuestra estimación

$\tau (1) + \tau(2) + \cdot\cdot\cdot + \tau(n) = n \log n + O(n).$

Es útil obtener una visión geométrica de este resultado. Claramente$\tau(r)$ es el número de puntos de celosía en la hipérbola$xy = r$,$x > 0$,$y > 0$. También, cada punto de celosía$(x, y)$$x > 0$,,$y > 0$$xy \le n$, yace sobre alguna hipérbola$xy = r$,$r \le n$. De ahí

$\sum_{n = 1}^{n} \tau(r)$

es el número de puntos de celosía en la región$xy \le n$,$x > 0$,$y > 0$. Si sumamos a lo largo de líneas verticales$x = 1, 2, ..., n$ obtenemos de nuevo

$\tau(1) + \tau (2) + \cdot\cdot\cdot \tau(n) = [\dfrac{n}{1}] + [\dfrac{n}{2}] + \cdot\cdot\cdot + [\dfrac{n}{n}]$.

En este enfoque, la simetría de$xy = n$ aproximadamente$x = y$ sugiere cómo mejorar esta estimación y obtener un término de error menor.

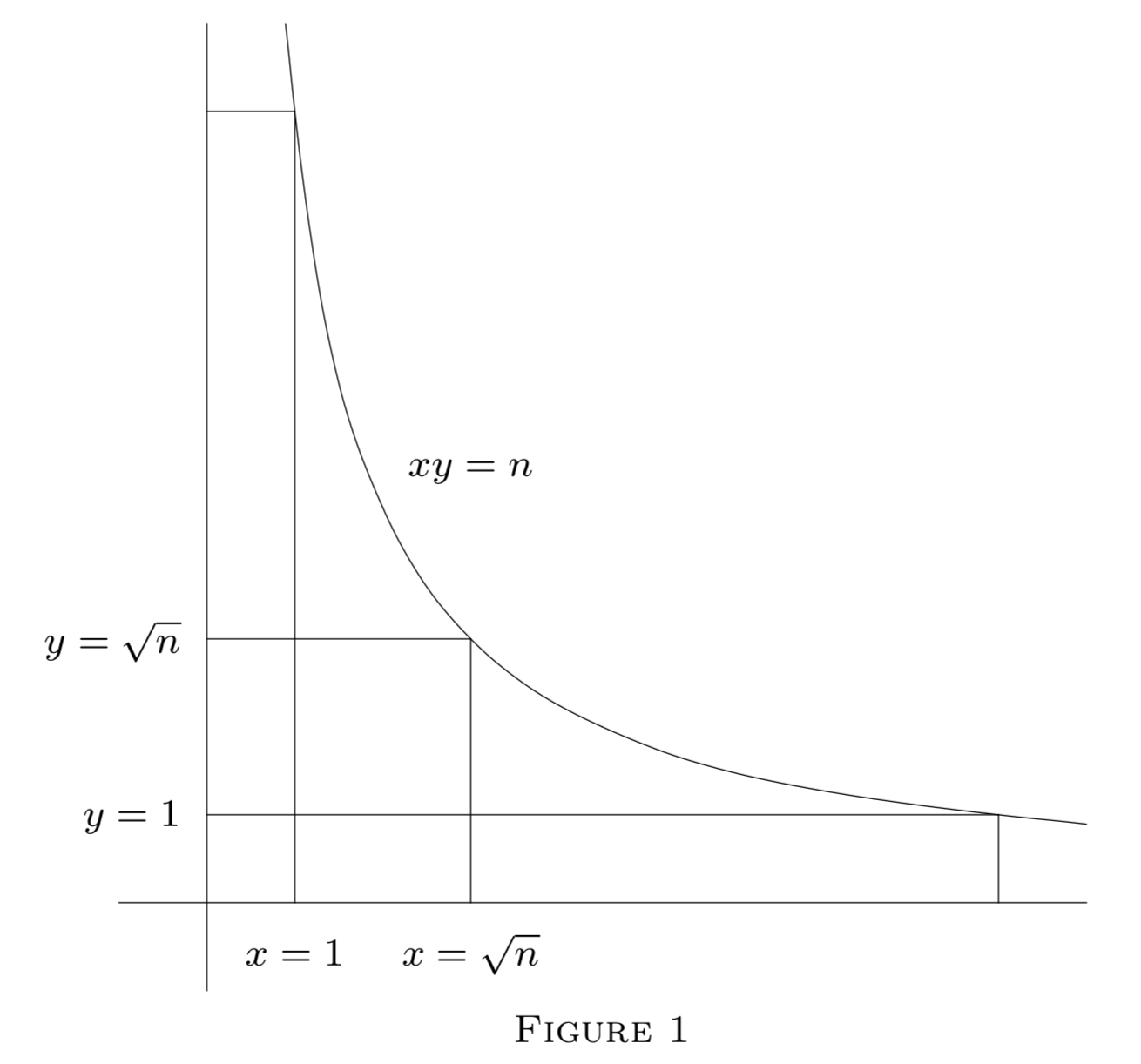
$2019-11-05 9.57.33.png$

Usando la simetría de la figura anterior, tenemos, con$u = [\sqrt{n}]$ y$h(n) = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}$,

$\begin{array} {rcl} {\sum_{r = 1}^{n} \tau(r)} &= & {2([\dfrac{n}{1}] + \cdot\cdot\cdot + [\dfrac{n}{u}]) - u^2} \\ {} &= & {2nh(u) - n + O(\sqrt{n})} \\ {} &= & {2n \log \sqrt{u} + (2 \gamma - 1)n + O(\sqrt{n})} \\ {} &= & {n \log n + (2 \gamma - 1)n + O(\sqrt{n}).} \end{array}$

Procediendo ahora a$\sum \sigma (r)$ que tenemos

$\sigma(1) + \sigma (2) + \cdot\cdot\cdot \sigma(n) = 1\ [\dfrac{n}{1}] + 2\ [\dfrac{n}{2}] + \cdot\cdot\cdot n\ [\dfrac{n}{n}].$

Con el fin de obtener una estimación de$\sum_{n = 1}^{x} \sigma (n)$ conjunto$k = 1$ en la identidad (obtenida anteriormente)

$\sigma_k(1) + \sigma_k (2) + \cdot\cdot\cdot \sigma_k (x) = \sum_{n = 1}^{x} (1^k + 2^k + \cdot\cdot\cdot + [\dfrac{x}{n}]^k).$

Tenemos inmediatamente

$\begin{array} {rcl} {\sigma (1) + \sigma (2) + \cdot\cdot\cdot \sigma (x)} & = & {\dfrac{1}{2} \sum_{n = 1}^{x} [\dfrac{x}{n}] [\dfrac{x}{n} + 1]} \\ {} & = & {\dfrac{1}{2} \sum_{n = 1}^{\infty} \dfrac{x^2}{n^2} + O(x \log x) = \dfrac{x^2 \zeta (2)}{2} + O(x \log x)} \\ {} & = & {\dfrac{\pi^2 x^2}{12} + O(x \log x).} \end{array}$

Para obtener estimaciones similares para$\varphi (n)$ observamos que$\varphi (r)$ es el número de puntos de celosía que se encuentran en el segmento de línea$x = r$$0 < y < r$,, y se puede ver desde el origen. (Un punto ($x, y$) se puede ver si$(x, y) = 1$.) Así$\varphi (1) + \varphi(2) + \cdot\cdot\cdot + \varphi (n)$ es el número de puntos de celosía visibles en la región con$n > x > y > 0$.

Consideremos un problema mucho más general, a saber, estimar el número de puntos de celosía visibles en una gran clase de regiones.

Heurísticamente podemos argumentar de la siguiente manera. Un punto$(x, y)$ es invisible en virtud de la prima$p$ si$p\ |\ x$ y$p\ |\ y$. La probabilidad de que esto ocurra es$\dfrac{1}{p^2}$. De ahí que la probabilidad de que el punto sea invisible es

$\prod_p (1 - \dfrac{1}{p^2}) = \prod_p (1 + \dfrac{1}{p^2} + \dfrac{1}{p^4} + \cdot\cdot\cdot)^{-1} = \dfrac{1}{\zeta (2)} = \dfrac{6}{\pi^2}.$

Por lo tanto, el número de punto de celosía visible debe ser$\dfrac{6}{\pi^2}$ multiplicado por el área de la región π. En particular el orden promedio de$\varphi(n)$ debe ser aproximadamente$\dfrac{6}{\pi^2} n$.

Ahora esbozamos una prueba del hecho de que en ciertas regiones grandes la fracción de puntos de celosía visibles contenidos en la región es aproximadamente$\dfrac{6}{\pi^2}$.

Le$R$ ser una región en el plano que tiene medida finita de Jordania y perímetro finito. Dejar$tR$ denotar la región obtenida al magnificar$R$ radialmente por$t$. $M (tR)$Sea el área de$tR$,$L(tR)$ el número de puntos de celosía en$tR$, y$V (tR)$ el número de puntos de celosía visibles en$tR$.

Es intuitivamente claro que

$L(tR) = M(tR) + O(t)$y$M(tR) = t^2 M(R)$.

Aplicando la fórmula de inversión a

$L(tR) = V(tR) + V(\dfrac{t}{2} R) + V(\dfrac{t}{3} R) + \cdot\cdot\cdot$

nos encontramos con que

$\begin{array} {V(tR)} & = & {\sum_{d = 1} L(\dfrac{t}{d} R) \mu (d) = \sum_{d = 1} M(\dfrac{t}{d} R) \mu (d)} \\ {} & \approx & {M(tR) \sum_{d = 1} \dfrac{\mu (d)}{d^2} \approx M(tR) \dfrac{6}{\pi^2} = t^2 M(R) \dfrac{6}{\pi^2}.} \end{array}$

Con$t = 1$ y$R$ la región$n > x > y > 0$, tenemos

$\varphi (1) + \varphi (2) + \cdot\cdot\cdot \varphi(n) \approx \dfrac{n^2}{2} \cdot \dfrac{6}{\pi^2} = \dfrac{3}{\pi^2} n^2$

Se ha demostrado (Chowla) que el término de error aquí no se puede reducir a$O(n \log \log \log n)$. Walfitz ha demostrado que puede ser reemplazado por$O(n \log ^{\dfrac{3}{4}} n)$.

Erd$ddot{o}$ s y Shapiro han demostrado que

$\varphi(1) + \varphi (2) + \cdot\cdot\cdot \varphi(n) - \dfrac{3}{\pi^2} n^2$

los cambios firman infinitamente a menudo.

Posteriormente haremos una aplicación de nuestra estimación de$\varphi(1) + \varphi (2) + \cdot\cdot\cdot \varphi(n)$ a la teoría de distribuciones de residuos cuadráticos.

Nuestro resultado también se puede interpretar como diciendo que si un par de enteros$(a, b)$

se eligen al azar la probabilidad de que sean relativamente primos es$\dfrac{6}{\pi^2}$.

En esta etapa señalamos sin pruebas una serie de resultados relacionados.

Si$(a, b)$ se eligen al azar el valor esperado de$(a, b)$ es$\dfrac{\pi^2}{6}$.

Si$f(x)$ es uno de una cierta clase de funciones aritméticas que incluye$x^{\alpha}$,$0 < \alpha < 1$, entonces la probabilidad que$(x, f(x)) = 1$ es$\dfrac{6}{\pi^2}$, y su valor esperado es$\dfrac{\pi^2}{6}$.

Este y los resultados relacionados fueron probados por Lambek y Moser.

La probabilidad de que$n$ los números elegidos al azar sean relativamente primos es$\dfrac{1}{\zeta(n)}$.

El número$Q(n)$ de números quadratfrei bajo$n$ es$\thicksim \dfrac{6}{\pi^2} n$ y el número$O_k (n)$ de números sin energía$k$ th bajo$n$ es$\dfrac{n}{\zeta(k)}.$ El primer resultado sigue casi inmediatamente de

$\sum Q (\dfrac{n^2}{r^2}) = n^2,$

para que por la fórmula de inversión

$Q(n^2) = \sum \mu(r) [\dfrac{n}{r}]^2 \thicksim n^2 \zeta (2).$

Un argumento más detallado arroja

$Q(x) = \dfrac{6x}{\pi^2} + O(\sqrt{x}).$

Otro resultado relacionado bastante divertido, cuya prueba se deja como ejercicio, es que

$\sum_{(a, b) = 1} \dfrac{1}{a^2b^2} = \dfrac{5}{2}.$

El resultado en se$Q(x)$ puede escribir en el formulario

$\sum_{n = 1}^{x} |\mu(n)| \thicksim \dfrac{6}{\pi^2} x$

Uno podría pedir estimaciones para

$\sum_{n = 1}^{x} \mu(n) = M(x).$

En efecto, se sabe (pero difícil de probar) eso$M(x) = o(x)$.

Demos la atención a$\omega (n)$. Tenemos

$\omega(1) + \omega(2) + \cdot\cdot\cdot \omega(n) = \sum_{p \le n} [\dfrac{n}{p}] \thicksim n\log \log n$.

Por lo tanto, el valor promedio de$\omega(n)$ es log log$n$.

Lo mismo sigue de manera similar para$\Omega (n)$

Un desarrollo relativamente reciente en esta línea, debido a Erd$\ddot{o}$ s, Kac, Leveque, Tatuzawa y otros es una serie de teoremas de los que es típico lo siguiente.

Dejar$A(x; \alpha, \beta)$ ser el número de enteros$n \le x$ para los cuales

$\alpha \sqrt{\log \log n} + \log \log n < \omega (n) < \beta \sqrt{\log \log n} + \log \log n.$

Entonces

$\text{lim}_{x \to \infty} \dfrac{A(x; \alpha, \beta)}{x} = \dfrac{1}{\sqrt{2\pi}} \int_{\alpha}^{\beta} e^{-\dfrac{u^2}{2}} du.$

Así tenemos por ejemplo eso$\omega (n) < \log \log n $ aproximadamente la mitad del tiempo.

También se puede Probar (Tatuzawa) que un resultado similar se mantiene para$B(x; \alpha, \beta)$, el número de enteros en el conjunto$f(1)$,$f(2)$,...,$f(x)$ ($f(x)$es un polinomio irreducible con coeficientes integrales) para lo cual$\omega (f(n))$ se encuentra en un rango similar a los prescritos para$\omega(n)$.

Otro tipo de resultado que tiene una aplicabilidad considerable es el siguiente.

El número$C(x, \alpha)$ de enteros$\le x$ que tienen un divisor primo$> x \alpha$,$1 > \alpha > \dfrac{1}{2}$, is$\thicksim -x \log \alpha$. De hecho, tenemos

$\begin{array} {rcl} {C(x, \alpha)} & = & {\sum_{x^{alpha} < p < x} \dfrac{x}{p} \thicksim x \sum_{x^{alpha} < p x} \dfrac{1}{p}} \\ {} & = & {x (\log \log x - \log \log \alpha)} \\ {} & = & {x (\log \log x - \log \log x - \log \alpha) = - x \log \alpha.} \end{array}$

Por ejemplo la densidad de números que tienen un factor primo superior a su raíz cuadrada es log 2$\approx$ .7.

Hasta ahora hemos considerado principalmente el comportamiento promedio de las funciones aritméticas. También podríamos indagar sobre límites absolutos. Uno puede demostrar sin dificultad que

$1 > \dfrac{varphi(n) \sigma(n)}{n^2} > \epsilon > 0$para todos$n$.

Además, se sabe que

$n > \varphi(n) > \dfrac{cn}{\log\log n}$

$n < \sigma(n) < cn \log\log n.$

En cuanto a$\tau(n)$, no es difícil demostrar que

$\tau (n) > (\log n)^k$

infinitamente a menudo por cada$k$ tiempo$\tau(n) < n^{\epsilon}$ por cada$\epsilon$ y$n$ suficiente grande.

Declaramos pero no probamos el teorema principal en esta línea.

Si$\epsilon > 0$ entonces

$\tau(n) < 2^{(1 + \epsilon) \log n / \log \log n}$para todos$n > n_0(\epsilon)$

mientras

$\tau(n) > 2^{(1 - \epsilon) \log n / \log \log n}$infinitamente a menudo.

Un tipo de problema algo diferente respecto al valor promedio de las funciones aritméticas fue el tema de una tesis de maestría de la Universidad de Alberta del señor R. Trollope hace un par de años.

Dejar$s_r(n)$ ser la suma de los dígitos de n cuando se escribe en base$r$. Mirsky ha demostrado que

$s_r(1) + s_r(2) + \cdot \cdot \cdot + s_r(n) = \dfrac{r - 1}{2} n \log_r n + O(n).$

El señor Trollope consideró sumas similares donde los elementos de la izquierda recorren ciertas secuencias como primos, cuadrados, etc.

Todavía otro resultado bastante divertido que obtuvo afirma que

$\dfrac{s_1(n) + s_2(n) + \cdot\cdot\cdot s_n(n)}{n^2} \thicksim 1 - \dfrac{\pi^2}{12}.$