1.4: Números irracionales

El más conocido de todos los números irracionales es\(\sqrt{2}\). Se establece\(\sqrt{2} \ne \dfrac{a}{b}\) con una prueba novedosa que no hace uso de argumentos de divisibilidad.

Supongamos\(\sqrt{2} = \dfrac{a}{b}\) (\(a\),\(b\) enteros), con\(b\) lo más pequeño posible. \(b < a < 2b\)Entonces para que

\(\dfrac{2ab}{ab} = 2\),\(\dfrac{a^2}{b^2} = 2,\) y\(\dfrac{2ab - a^2}{ab - b^2} = 2 = \dfrac{a(2b - a)}{b(a - b)}\).

Así

\(\sqrt{2} = \dfrac{2b - a}{a - b}\).

Pero\(a < 2b\) y\(a - b < b\); de ahí tenemos una representación racional de\(\sqrt{2}\) con denominador más pequeño que el más pequeño posible!

Para convencer a los estudiantes de la existencia de irracionales se podría comenzar con una prueba de la irracionalidad de\(\log_{10} 2\). Si\(\log_{10} 2 = \dfrac{a}{b}\) entonces\(10^{a/b} = 2\) o\(10^a = 2^b\). Pero ahora el lado izquierdo es divisible por 5 mientras que el lado derecho no lo es.

Tampoco tan familiar como debería ser es el hecho de que\(\cos 1^{\circ}\) (y\(\sin 1^{\circ}\)) es irracional. Desde

\(\cos 45^{\circ} + i \sin 45^{\circ} = (\cos 1^{\circ} + i \sin 1^{\circ})^{45}\)

deducimos que se\(45^{\circ}\) puede expresar como un polinomio en coeficientes enteros en\(\cos 1^{\circ}\). De ahí que si\(\cos 1^{\circ}\) fueran racionales así sería\(\cos 45^{\circ} = \dfrac{1}{\sqrt{2}}\).

El hecho de que

\(\cos 1 = 1 - \dfrac{1}{2!} + \dfrac{1}{4!} - \cdot\cdot\cdot\)

es irracional se puede probar de la misma manera que la irracionalidad de\(e\). En este último caso, asumiendo\(e\) racional,

\(\dfrac{b}{a} = e = 1 + \dfrac{1}{1!} + \dfrac{1}{2!} + \cdot\cdot\cdot + \dfrac{1}{(a + 1)!} + \dfrac{1}{(a + 2)!} + \cdot\cdot\cdot\),

lo que, tras la multiplicación por\(a!\), implicaría que\(\dfrac{1}{a + 1} + \dfrac{1}{(a + 1)(a + 2)} + \cdot\cdot\cdot\) es un entero positivo menor que 1.

Se puede utilizar un argumento un poco más complicado para mostrar que no\(e\) es de irracionalidad cuadrática, es decir, que si\(a, b, c\) son enteros entonces\(ae^2 + be + c \ne 0\). No obstante, una prueba de la trascendentalidad de todavía no\(e\) es fácil. Las primeras ediciones de Hardy y Wright afirmaron que no había pruebas fáciles de que π sea trascendental pero esta situación fue rectificada en 1947 por I. Niven cuya prueba de la irracionalidad de la\(\pi\) que ahora presentamos.

Vamos

\(\pi = \dfrac{a}{b}, f(x) = \dfrac{x^n (a - by)^n}{n!}\), y\(F(x) = f(x) - f^{(2)}(x) + f^{(4)}(x) - \cdot\cdot\cdot,\)

el entero positivo\(n\) que se especifica más adelante. Ya que\(n!f(x)\) tiene coeficientes integrales y\(x\) términos en grado\(\le 2n\),\(f(x)\) y todas sus derivadas tendrán valores integrales en\(x= 0\). También para\(x = \pi = \dfrac{a}{b}\), ya que\(f(x) = f(\dfrac{a}{b} - x)\). Por cálculo elemental tenemos

\(\dfrac{d}{dx} [F'(x) \sin x - F(x) \cos x] = F'' (x) \sin x + F(x) \sin x = f(x) \sin x.\)

De ahí

\(\int_{0}^{\pi} f(x) \sin x dx = [F'(x) - F(x) \cos x]_{0}^{\pi} =\)un entero.

Sin embargo, para\(0 < x < \pi\),

\(0 < f(x) \sin x < \dfrac{\pi^n a^n}{n!} \to 0\)

para grandes\(n\). De ahí que la integral definida sea positiva pero arbitrariamente pequeña para grande\(n\); esta contradicción demuestra que el supuesto\(\pi = \dfrac{a}{b}\) es insostenible.

Esta prueba se ha extendido de diversas maneras. Por ejemplo, Niven también demostró que el coseno de un número racional es irracional. Si ahora\(\pi\) fueran racionales,\(\cos \pi = −1\) sería irracional. Además, el método también puede ser utilizado para probar la irracionalidad de ciertos números definidos como las raíces de las soluciones de ecuaciones diferenciales de segundo orden que satisfacen condiciones especiales de límite. Recientemente se ha dado una variación de la prueba de Niven que, aunque más complicada, evita el uso de integrales o series infinitas. Todavía falta una prueba realmente simple que\(\pi\) sea trascendental, es decir, que no satisfaga ninguna ecuación polinómica con coeficientes enteros.

Con respecto a los números trascendentales existen esencialmente tres tipos de problemas: probar la existencia de tales números, construir tales números, y finalmente (y esto es mucho más difícil que los dos primeros) probar que ciertos números que surgen naturalmente en el análisis son trascendentales. Ejemplos de números que se han demostrado trascendentales son\(\pi\),\(e\),\(e^{-\pi}\), y\(\dfrac{\log 3}{\log 2}\). Es interesante comentar aquí que la constante de Euler\(\gamma\) y

\(\sum_{n = 1}^{\infty} \dfrac{1}{n^{2s + 1}}\)(\(s\)es un entero)

ni siquiera se han demostrado irracionales.

La prueba de Cantor de la existencia de números trascendentales procede mostrando que los números algebraicos son contables mientras que los números reales no lo son. Así, cada conjunto incontable de números contiene números trascendentales. Por ejemplo hay un número trascendental de la forma\(e^{i\theta}\)\(0 < \theta < \dfrac{\pi}{2}\), digamos.

Aunque aquí no es del todo relevante realizaremos ahora un pequeño truco de desaparición utilizando un número tan trascendental\(e^{i\theta}\) y una construcción debido a Kuratowski.

Considera el siguiente conjunto de puntos en el plano complejo. Comience con el punto\(O\) y deje\(\tilde{S}\) ser el conjunto de todos los puntos obtenibles de él por una sucesión de las operaciones de trasladar los puntos 1 unidad a la derecha y girarlos en un ángulo\(\theta\) alrededor\(O\). Si denotamos tales traducciones y rotaciones por\(T\) y\(R\) respectivamente entonces un punto típico de nuestro conjunto\(\tilde{S}\) puede ser denotado por\(T^{a}R^{b}T^{c}R^{d} \cdot\cdot\cdot\). A continuación observamos que cada punto de\(\tilde{S}\) debe tener una representación única en esta forma. En efecto,\(T\) significa sumar 1 al número complejo correspondiente al punto y\(R\) significa multiplicar por\(e^{i\theta}\). De ahí que todos nuestros puntos sean polinomios adentro\(e^{i\theta}\) con coeficientes positivos, digamos\(z = P (e^{i\theta})\). Pero ahora si un punto tiene una doble representación, entonces\(P (e^{i\theta}) = R(e^{i\theta})\) y obtendríamos un polinomio en el\(e^{i\theta}\) que negaría el carácter trascendental de\(e^{i\theta}\).

Vamos a\(\tilde{T}\) denotar el subconjunto del\(\tilde{S}\) cual consiste en aquellos puntos de\(\tilde{S}\) para los cuales la última operación necesaria para alcanzarlos es a\(T\), y vamos\(\tilde{R}\) denotar el subconjunto que consiste en aquellos puntos de\(\tilde{S}\) para los cuales la última operación necesaria para alcanzarlos es una\(R\). Claramente\(\tilde{S} = \tilde{T} \cup \tilde{R}\) y\(\tilde{T} \cap \tilde{R} = \emptyset\). Una traducción\(\tilde{S}\) de una unidad a la derecha envía\(\tilde{S}\) a\(\tilde{T}\), es decir, ¡hace\(\tilde{R}\) desaparecer! Por otro lado, ¡una rotación del avión a través de\(\theta\) envía\(\tilde{S}\) a\(\tilde{R}\) hacer\(\tilde{T}\) desaparecer!

Hasta el momento sólo hemos discutido la existencia de números trascendentales. El enfoque más fácil para la construcción real de tales números es a través de un teorema debido a Liouville.

Decimos que un número algebraico es de grado\(n\) si satisface una ecuación polinómica de grado\(n\). Decimos que un número real\(\lambda\) es aproximable al orden\(n\) siempre que la desigualdad

\(|\lambda - \dfrac{a}{b}| < \dfrac{c}{b^n}\)

tiene infinidad de soluciones para alguna constante\(c\). El teorema de Liouville afirma que un número algebraico real de grado no\(n\) es aproximable a ningún orden mayor que\(n\).

Supongamos que\(\lambda\) es de grado\(n\). Entonces satisface una ecuación

\(f(\lambda) = a_0 \lambda^n + a_1 \lambda^{n - 1} + \cdot\cdot\cdot + a_n = 0.\)

Hay un número\(M = M(\lambda)\) tal que\(|f'(x)| < M\) donde\(\lambda - 1 < x < \lambda + 1\). Supongamos ahora que\(\dfrac{p}{1} \ne \lambda\) es una aproximación a\(\lambda\). Podemos suponer la aproximación lo suficientemente buena como para asegurar que\(\dfrac{p}{q}\) se encuentra en el intervalo\(\lambda - 1, \lambda + 1)\),

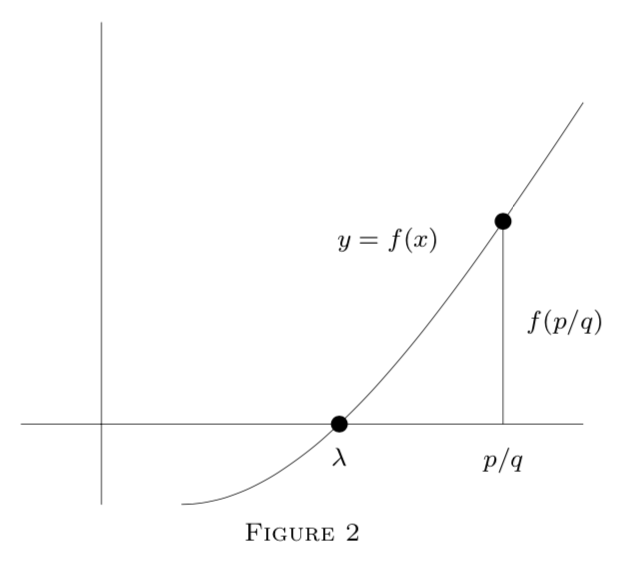
y está más cerca\(\lambda\) que cualquier otra raíz de\(f(x) = 0\), así que eso\(f(p/q) \ne 0\).

Claramente (ver Figura 2),

\(|f(\dfrac{p}{q})| = \dfrac{1}{q^n} |a_0p^n + a_1 p^{n - 1} q + \cdot\cdot\cdot + a_n q^n| \ge \dfrac{1}{q^n}\)

y

\(|dfrac{f(p/q)}{\lambda - p/q}| < M\)

para que

\(|\lambda - \dfrac{p}{q}| > \dfrac{c}{q^n}\)

y se prueba el teorema.

Aunque el teorema de Liouville es suficiente para la construcción de muchos números trascendentales, mucho interés se centra en ciertos refinamientos. En particular, es deseable tener un teorema del siguiente tipo. Si\(\lambda\) es de grado\(n\) entonces

\(|\lambda - \dfrac{p}{q}| < \dfrac{M}{q^{f(n)}}\)

tiene como máximo un número finito de soluciones. Aquí\(f(n)\) puede tomarse como\(n\) por el teorema de Liouville. ¿Se puede disminuir? Thue, alrededor de 1909, primero demostró que uno podía tomar\(f(n) = \dfrac{n}{2}\) y Siegel (1921) demostró que podemos tomar\(f(n) = 2\sqrt{n}\). Esto fue ligeramente mejorado por Dyson y Schneider para\(\sqrt{2n}\). Muy recientemente (1955), F. K. Roth creó sensación al demostrar que podemos tomar\(f(n) = 2 + \epsilon\). Su prueba es larga y complicada. Que no podemos tomar\(f(n) = 2\) (de ahí que el resultado de Roth sea de la mejor manera posible) se puede ver a partir del siguiente resultado debido a Dirichlet.

Por irracional\(\lambda\) existen infinitamente muchas soluciones de

\(|\lambda - \dfrac{p}{q}| < \dfrac{1}{q^2}.\)

La prueba no es difícil,\(\lambda\) seamos irracionales y consideremos, para fijos\(n\), los números (\(\lambda\)), (\(2 \lambda\)),..., (\(n \lambda\)), donde\((x)\) significa “parte fraccionaria de\(x\)”. Estos\(n\) puntos son puntos distintos sobre\(0, 1)\); de ahí que existan dos de ellos dicen\(i\lambda\) y\(j \lambda\) cuya distancia es\(\le \dfrac{1}{n}\). Así tenemos

\((i\lambda) - (j \lambda) < \dfrac{1}{n}\)

o

\(k \lambda - m \le \dfrac{1}{n}\)(\(k\)y\(m\) enteros\(\le n\))

y

\(|\lambda - \dfrac{m}{k}| \le \dfrac{1}{nk} \le \dfrac{1}{n^2},\)

según se requiera.

Volvemos ahora a la aplicación del teorema de Liouville a la construcción de números trascendentales.

Considerar

\(\dfrac{1}{10^{1!}} + \dfrac{1}{10^{2!}} + \cdot\cdot\cdot + \dfrac{1}{10^{p!}} = \lambda_p\)

así como el número real\(\lambda = \lambda_{\infty}\). Se comprueba fácilmente eso\(|\lambda_{\infty} - \lambda_p| < \dfrac{1}{\lambda^{n + 1}\) para cada\(p\). De ahí\(\lambda\) que sea aproximable al orden\(n\) para cualquiera\(n\) y por lo tanto no es algebraico.