6.4: Simulación de modelos de tiempo continuo
- Page ID
- 115719
La simulación de un modelo de tiempo continuo equivale a la integración numérica de ecuaciones diferenciales, que, por sí misma, es una importante área de investigación en matemáticas aplicadas y ciencias computacionales con más de un siglo de historia. Hay una gran cantidad de metodologías desarrolladas para lograr integraciones numéricas precisas, rápidas y eficientes. Fácilmente tomaría algunos libros y semestres para cubrirlos, y este libro de texto no pretende hacer eso. En cambio, aquí nos enfocamos en el método más simple posible para simular un modelo de tiempo continuo, usando la siguiente fórmula como aproximación de una ecuación diferencial
\[\begin{align} \dfrac{dx}{dt} &=G(x); \\[4pt] x(t+\Delta{t}) &= x(t) +G(x(t))\Delta{t} \label{6.26} \end{align} \]
Este método se llama el método de avance de Euler. Su idea básica es muy sencilla; solo sigues acumulando pequeños aumentos/disminuciones de lo\(x\) que se espera de las derivadas locales especificadas en la ecuación diferencial original. La secuencia producida por esta fórmula discretizada se acercará a la verdadera solución de la ecuación diferencial original en el\(\displaystyle \lim_{∆t → 0}\), aunque en la práctica, este método es menos preciso para el tamaño finito\(∆t\) que otros métodos más sofisticados (ver Ejercicio 6.6.3). Dicho esto, su intuitividad y facilidad de implementación tienen un mérito, especialmente para aquellos que son nuevos en la simulación por computadora. Entonces, apegémonos a este método por ahora.
En casi todos los aspectos, la simulación de modelos de tiempo continuo utilizando el método Euler forward es idéntica a la simulación de modelos de tiempo discreto que discutimos en el Capítulo 4. Probablemente la única diferencia técnica es que tenemos\(∆t\) como tamaño de paso para el tiempo, que puede no ser 1, por lo que también necesitamos hacer un seguimiento del avance del tiempo además del avance de las variables de estado. Trabajemos en el siguiente ejemplo para ver cómo implementar el método forward de Euler.
Aquí consideramos simular el siguiente modelo de crecimiento logístico de tiempo continuo para\(0 ≤ t < 50\) en Python, con\(x(0) = 0.1\)\(r = 0.2\),\(K = 1\) y\(∆t = 0.01\):
\[\frac{dx}{dt} =rx(1-\frac{x}{K}) \label{6.27} \]
Lo primero (y único) que tenemos que hacer es discretizar el tiempo en el modelo anterior. Usando la ecuación\ ref {6.26}, la ecuación se convierte en
\[x(t+\Delta{t}) =x(t) +rx(t)(1 -\frac{x(t)}{K}) \Delta{t}, \label{6.28} \]
que no es más que una típica ecuación de diferencia. Entonces, podemos revisar fácilmente el Código 4.10 para crear un simulador de Ecuación\ ref {6.27}:


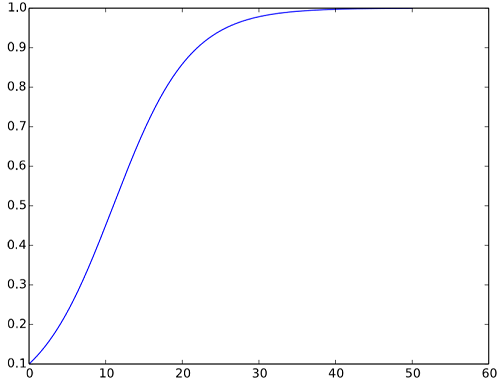
\(∆t\)Varía para tener valores mayores en el ejemplo anterior y ver cómo el resultado de la simulación se ve afectado por dichos cambios.
Como lo ilustra el ejercicio anterior, la integración numérica de ecuaciones diferenciales implica algunas cuestiones técnicas, como la estabilidad y convergencia de soluciones y la posibilidad de “artefactos” derivados de la discretización del tiempo. Siempre debe estar atento a estos problemas y tener cuidado al implementar códigos de simulación para modelos de tiempo continuo. Espero que los siguientes ejercicios te ayuden a investigar más a fondo esas sutilezas de la integración numérica de ecuaciones diferenciales.
Simule el siguiente modelo Lotka-Volterra (presa depredadora) en tiempo continuo para\(0 ≤ t < 50\) en Python, con\(x(0) = y(0) = 0.1\),\(a = b = c = d = 1\) y\(∆t = 0.01\). Visualice los resultados de la simulación en el tiempo y también en un espacio de fase.
\[\frac{dx}{dt} =ax-bxy \label{6.29} \]
Existen muchos otros métodos más sofisticados para la integración numérica de ecuaciones diferenciales, como el método de Euler hacia atrás, el método de Heun, los métodos Runge-Kutta, etc. Investiga algunos de esos métodos para ver cómo funcionan y por qué sus resultados son mejores que los del método forward de Euler.

