1.14: Números Complejos
- Page ID
- 117016
Ver tutorial en YouTube: Números complejos
Ver tutorial en YouTube: Función Exponencial Compleja
Definimos el número\(i\) imaginario como uno de los dos números que satisface la regla\((i)^2 = −1\), siendo el otro número\(−i\). Formalmente, escribimos\(i =\sqrt{−1}\). Un número complejo\(z\) se escribe como\[z=x+iy,\nonumber\] dónde\(x\) y\(y\) son números reales. Llamamos a\(x\) la parte real de\(z\) y a\(y\) la parte imaginaria y escribimos\[x=\text{Re }z,\quad y=\text{Im }z.\nonumber\]
Dos números complejos son iguales si y sólo si sus partes reales e imaginarias son iguales.
El complejo conjugado de\(z = x + iy\), denotado como\(\overline{z}\), se define como\[\overline{z}=x-iy.\nonumber\]
Usando\(z\) y\(\overline{z}\), tenemos\[\label{eq:1}\text{Re }z=\frac{1}{2}(z+\overline{z}),\quad\text{Im }z=\frac{1}{2i}(z-\overline{z}).\]
Además,\[\begin{aligned}z\overline{z}&=(x+iy)(x-iy) \\ &=x^2-i^2y^2 \\ &=x^2+y^2;\end{aligned}\] y definimos el valor absoluto de\(z\), también llamado el módulo de\(z\), por\[\begin{aligned} |z|&=(z\overline{z})^{1/2} \\ &=\sqrt{x^2+y^2}.\end{aligned}\]
Podemos sumar, restar, multiplicar y dividir números complejos para obtener nuevos números complejos. Con\(z = x + iy\) y\(w = s + it\), y números\(x,\)\(y,\)\(s,\)\(t\) reales, tenemos\[ z + w = (x + s) + i(y + t);\quad z − w = (x − s) + i(y − t);\nonumber\]
\[\begin{aligned} zw&=(x+iy)(s+it) \\ &=(xs-yt)+i(xt+ys); \\ & \\ \frac{z}{w}&=\frac{z\overline{w}}{w\overline{w}} \\ &=\frac{(x+iy)(s-it)}{s^2+t^2} \\ &=\frac{(xs+yt)}{s^2+t^2}+i\frac{(ys-xt)}{s^2+t^2}.\end{aligned}\]
Además,\[\begin{aligned} |zw|&=\sqrt{(xs-yt)^2+(xt+ys)^2} \\ &=\sqrt{(x^2+y^2)(s^2+t^2)} \\ &=|z||w|;\end{aligned}\] y\[\begin{aligned}\overline{zw}&=(xs-yt)-i(xt+ys) \\ &=(x-iy)(s-it) \\ &=\overline{z}\overline{w}.\end{aligned}\]
Del mismo modo\[\left|\frac{z}{w}\right| =\frac{|z|}{|w|},\quad\overline{\left(\frac{z}{w}\right)}=\frac{\overline{z}}{\overline{w}}.\nonumber\]
También,\(\overline{z + w} = \overline{z} + \overline{w}\). Sin embargo,\(|z + w| ≤ |z| + |w|\), un teorema conocido como el triángulo de la desigualdad.
Es especialmente interesante y útil considerar la función exponencial de un argumento imaginario. Usando la expansión de la serie Taylor de una función exponencial, tenemos\[\begin{aligned}e^{i\theta}&=1+(i\theta )+\frac{(i\theta )^2}{2!}+\frac{(i\theta )^3}{3!}+\frac{(i\theta )^4}{4!}+\frac{(i\theta )^5}{5!}\cdots \\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\cdots\right)+i\left(\theta -\frac{\theta^3}{3!}+\frac{\theta^5}{5!}+\cdots\right) \\ &=\cos\theta +i\sin\theta.\end{aligned}\]
Ya que hemos determinado que también\[\label{eq:2}\cos\theta=\text{Re }e^{i\theta },\quad\sin\theta =\text{Im }e^{i\theta },\] tenemos usando\(\eqref{eq:1}\) y\(\eqref{eq:2}\), las expresiones de uso frecuente\[\cos\theta =\frac{e^{i\theta}+e^{-i\theta }}{2},\quad\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}.\nonumber\]
La tan célebre identidad de Euler deriva\(e^{iθ} = \cos θ + i \sin θ\) de establecer\(θ = π\), usar\(\cos π = −1\) y\(\sin π = 0\):
\[e^{i\pi}+1=0,\nonumber\]y esta identidad vincula los cinco números fundamentales\(0,\: 1,\: i,\: e\) —y\(π\) —utilizando tres operaciones matemáticas básicas —suma, multiplicación y exponenciación—solo una vez.
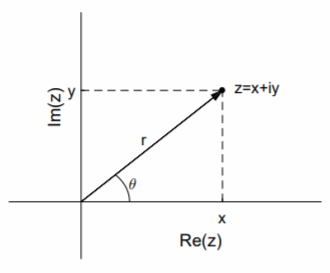
El número complejo se\(z\) puede representar en el plano complejo con\(\text{Re }z\) como\(x\) eje -eje y\(\text{Im }z\) como\(y\) eje -eje (ver Figura\(\PageIndex{1}\)). Esto lleva a la representación polar de\(z = x + iy\):
\[z=re^{i\theta},\nonumber\]dónde\(r = |z|\) y\(\tan θ = y/x\). Definimos\(\text{arg }z = θ\). Tenga en cuenta que no\(θ\) es único, aunque es convencional elegir el valor tal que\(−π < θ ≤ π\), y\(θ = 0\) cuándo\(r = 0\).
La forma polar de un número complejo puede ser útil al multiplicar números. Por ejemplo, si\(z_1=r_1e^{i\theta _1}\) y\(z_2=r_2e^{i\theta _2}\), entonces\(z_1z_2 = r_1r_2e^{i(θ_1+θ_2)}\). En particular, si\(r_2 = 1\), entonces multiplicación de\(z_1\) por\(z_2\) giros la representación de\(z_1\) en el plano complejo un ángulo en\(θ_2\) sentido antihorario.
Se pueden derivar relaciones trigonométricas útiles usando\(e^{iθ}\) y propiedades de la función exponencial. La ley de adición puede derivarse de\[e^{i(x+y)}=e^{ix}e^{iy}.\nonumber\]
Tenemos\[\begin{aligned} \cos(x + y) + i \sin(x + y) &= (\cos x + i \sin x)(\cos y + i \sin y) \\ &= (\cos x \cos y − \sin x \sin y) + i(\sin x \cos y + \cos x \sin y);\end{aligned}\] rindiendo\[ \cos(x + y) = \cos x \cos y − \sin x \sin y,\quad \sin(x + y) = \sin x \cos y + \cos x \sin y.\nonumber\]
El teorema de De Moivre deriva de\(e^{inθ} = (e^{iθ})^n\), cediendo la identidad\[\cos(nθ) + i \sin(nθ) = (\cos θ + i \sin θ)^n.\nonumber\]
Por ejemplo, si\(n=2\), derivamos\[\begin{aligned} \cos 2\theta +i\sin 2\theta &=(\cos\theta +i\sin\theta)^2 \\ &=(\cos^2\theta -\sin^2\theta)+2i\cos\theta\sin\theta.\end{aligned}\]
Por lo tanto,\[\cos 2θ = \cos^2 θ − \sin^2 θ,\quad \sin 2θ = 2 \cos θ \sin θ.\nonumber\]
Escribir\(\sqrt{i}\) como un número complejo estándar
Solución
Para resolver este ejemplo, primero necesitamos definir qué se entiende por la raíz cuadrada de un número complejo. El significado de\(\sqrt{z}\) es el número complejo cuyo cuadrado es\(z\). Siempre habrá dos de esos números, porque\((\sqrt{z})^2 = (−\sqrt{z})^2 = z\). No se puede definir la raíz cuadrada positiva porque los números complejos no se definen como positivos o negativos.
Mostraremos dos métodos para resolver este problema. El primer método más sencillo escribe\[\sqrt{i}=x+iy.\nonumber\]
Al cuadrar ambos lados, obtenemos\[i=x^2-y^2+2xyi;\nonumber\] e igualando las partes real e imaginaria de esta ecuación arroja las dos ecuaciones reales\[x^2-y^2=0,\quad 2xy=1.\nonumber\]
La primera ecuación rinde\(y = ±x\). Con\(y = x\), la segunda ecuación rinde\(2x^2 = 1\) con dos soluciones\(x = ±\sqrt{2}/2\). Con\(y = −x\), la segunda ecuación rinde\(−2x^2 = 1\), que no tiene solución real\(x\). Por lo tanto, hemos encontrado que\[\sqrt{i}=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
El segundo método de solución hace uso de la forma polar de números complejos. El álgebra que se requiere para este método es algo más sencillo, sobre todo para encontrar raíces cubitas, cuartas raíces\(i = e^{iπ/2}\), etc. Sabemos que, pero de manera más general por la naturaleza periódica del ángulo polar, podemos escribir\[i=e^{i(\frac{\pi}{2}+2\pi k)},\nonumber\] donde\(k\) es un entero. Entonces tenemos\[\sqrt{i}=i^{1/2}=e^{i(\frac{\pi}{4}+\pi k)}=e^{i\pi k}e^{i\pi /4}=\pm e^{i\pi /4},\nonumber\] donde hemos hecho uso de las propiedades habituales de la función exponencial, y\(e^{iπk} = ±1\) para par o\(k\) impar. Volviendo a la forma estándar, tenemos\[\sqrt{i}=\pm (\cos \pi /4+i\sin \pi /4)=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
El teorema fundamental del álgebra establece que cada ecuación polinómica de grado\(n\) tiene raíces exactamente\(n\) complejas, contadas con multiplicidad. Dos ejemplos familiares serían\(x^2 − 1 = (x + 1)(x − 1) = 0\), con dos raíces\(x_1 = −1\) y\(x_2 = 1\); y\(x^2 − 2x + 1 = (x − 1)^2 = 0\), con una raíz\(x_1 = 1\) con multiplicidad dos.
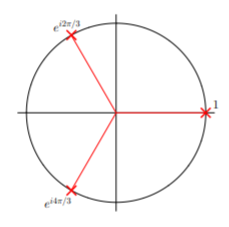
El problema de encontrar las raíces\(n\) th de la unidad es resolver la ecuación polinómica\[z^n=1\nonumber\] para los valores\(n\) complejos de\(z\). Tenemos\(z_1 = 1\) para\(n = 1\); y\(z_1 = 1\),\(z_2 = −1\) para\(n = 2\). Más allá\(n = 2\), algunas de las raíces son complejas y aquí encontramos las raíces cubo de la unidad, es decir, los tres valores de\(z\) que satisfacen\(z^3 = 1\). Escribiendo\(1 = e^{i2πk}\), donde\(k\) es un entero, tenemos\[z=(1)^{1/3}=\left(e^{i2\pi k}\right)^{1/3}=e^{i2\pi k/3}=\left\{\begin{array}{l}1; \\ e^{i2\pi /3}; \\ e^{i4\pi /3}.\end{array}\right.\nonumber\]
\(\cos (2π/3) = −1/2,\)\(\sin (2π/3) = \sqrt{3}/2,\)\(\cos (4π/3) = −1/2,\)\(\sin (4π/3) = − \sqrt{3}/2,\)El uso de las tres raíces cubicas de la unidad viene dado por\[z_1=1,\quad z_2=-\frac{1}{2}+i\frac{\sqrt{3}}{2},\quad z_3=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.\nonumber\]
Estas tres raíces están espaciadas uniformemente alrededor del círculo unitario en el plano complejo, como se muestra en la siguiente figura.
