3.2: Ecuaciones separables

Ver tutorial en YouTube

Una oda de primer orden es separable si se puede escribir en la forma en \[\label{eq:1}g(y)\frac{dy}{dx}=f(x),\quad y(x_0)=y_0,\]que la función\(g(y)\) es independiente\(x\) y\(f(x)\) es independiente de\(y\). Integración de\(x_0\) a\(x\) resultados en\[\int_{x_0}^xg(y(x))y'(x)dx=\int_{x_0}^xf(x)dx.\nonumber\]

La integral de la izquierda se puede transformar sustituyendo\(u = y(x),\: du = y'(x)dx\), y cambiando los límites inferior y superior de integración a\(y(x_0) = y_0\) y\(y(x) = y\). Por lo tanto,\[\int_{y_0}^yg(u)du=\int_{x_0}^xf(x)dx,\nonumber\] y dado que\(u\) es una variable ficticia de integración, podemos escribir esto en la forma equivalente \[\label{eq:2}\int_{y_0}^yg(y)dy=\int_{x_0}^xf(x)dx.\]

Un procedimiento más sencillo que también rinde\(\eqref{eq:2}\) es tratar\(dy/dx\)\(\eqref{eq:1}\) como una fracción. Multiplicando\(\eqref{eq:1}\) por\(dx\) resultados en la\[g(y)dy=f(x)dx,\nonumber\] que se encuentra una ecuación separada con todas las variables dependientes en el lado izquierdo, y todas las variables independientes en el lado derecho. La ecuación\(\eqref{eq:2}\) luego resulta directamente sobre la integración.

Ejemplo\(\PageIndex{1}\)

Resolver\(\frac{dy}{dx}+\frac{1}{2}y=\frac{3}{2}\), con\(y(0)=2\).

Solución

Primero manipulamos la ecuación diferencial a la forma \[\label{eq:3}\frac{dy}{dx}=\frac{1}{2}(3-y),\]y luego tratamos\(dy/dx\) como si fuera una fracción para separar variables:

\[\frac{dy}{3-y}=\frac{1}{2}dx.\nonumber\]

Integramos el lado derecho desde la condición inicial\(x = 0\) hasta\(x\) y el lado izquierdo desde la condición inicial\(y(0) = 2\) hasta\(y\). En consecuencia, \[\label{eq:4}\int_2^y\frac{dy}{3-y}=\frac{1}{2}\int_0^xdx.\]

Las integrales en\(\eqref{eq:4}\) necesidad de hacerse. Tenga en cuenta que\(y(x) < 3\) para finitos\(x\) o la integral en el lado izquierdo diverge. Por lo tanto,\(3 − y > 0\) y rendimientos de integración\[\begin{aligned} -\ln (3-y)]_2^y&=\frac{1}{2}x]_0^x, \\ \ln(3-y)&=-\frac{1}{2}x, \\ 3-y&=e^{-\frac{1}{2}x}, \\ y&=3-e^{-\frac{1}{2}x}.\end{aligned}\]

Dado que esta es nuestra primera solución analítica no trivial, es prudente verificar nuestro resultado. Esto lo hacemos diferenciando nuestra solución:

\[\begin{aligned}\frac{dy}{dx}&=\frac{1}{2}e^{-\frac{1}{2}x} \\ &=\frac{1}{2}(3-y);\end{aligned}\]y comprobando las condiciones iniciales,\(y(0) = 3 − e^0 = 2\). Por lo tanto, nuestra solución satisface tanto la oda original como la condición inicial.

Ejemplo\(\PageIndex{2}\)

Resolver\(\frac{dy}{dx}+\frac{1}{2}y=\frac{3}{2},\) con\(y(0)=4\).

Solución

Esta es la ecuación diferencial idéntica a la anterior, pero con diferentes condiciones iniciales. Saltaremos directamente al paso de integración:

\[\int_4^y\frac{dy}{3-y}=\frac{1}{2}\int_0^xdx.\nonumber\]

Ahora\(y(x) > 3\), para que\(y − 3 > 0\) y la integración rinda\[\begin{aligned}-\ln (y-3)]_4^y&=\frac{1}{2}x]_0^x, \\ \ln(y-3)&=-\frac{1}{2}x, \\ y-3&=e^{-\frac{1}{2}x}, \\ y&=3+e^{-\frac{1}{2}x}.\end{aligned}\]

Figura\(\PageIndex{1}\): Solución de la siguiente ODE:\(\frac{dy}{dx}+\frac{1}{2}y=\frac{3}{2}\).

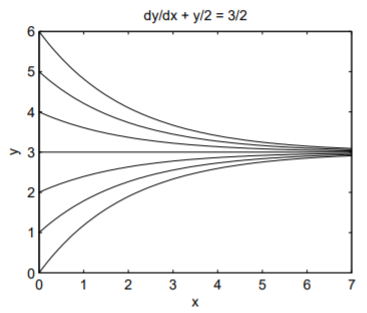
Las curvas de solución para un rango de condiciones iniciales se presentan en la Fig. \(\PageIndex{1}\). Todas las soluciones tienen una asíntota horizontal\(y = 3\) en la que\(dy/dx = 0\). Para\(y(0) = y_0\), se puede demostrar que la solución general es\(y(x) = 3 + (y_0 − 3) \text{exp}(−x/2)\).

Ejemplo\(\PageIndex{3}\)

Resolver\(\frac{dy}{dx}=\frac{2\cos 2x}{3+2y}\), con\(y(0)=-1\).

1. ¿Para qué valores de\(x>0\) existe la solución?
2. ¿Para qué valor de\(x>0\) es\(y(x)\) máximo?

Solución

Observe que el derivado de\(y\) diverge cuando\(y = −3/2\), y que esto puede ocasionar algunos problemas con una solución.

Resolvemos la oda separando variables e integrando de las condiciones iniciales:

\[\begin{aligned} (3+2y)dy&=2\cos 2xdx \\ \int_{-1}^y(3+2y)dy&=2\int_0^x\cos 2xdx \\ 3y+y^2]_{-1}^y&=\sin 2x]_0^x \\ y^2+3y+2-\sin 2x&=0 \\ y_{\pm} &=\frac{1}{2}[-3\pm\sqrt{1+4\sin 2x}].\end{aligned}\]

Resolver la ecuación cuadrática para\(y\) ha introducido una solución espuria que no satisface las condiciones iniciales. Probamos:

\[y_{\pm}(0)=\frac{1}{2}[-3\pm 1]=\left\{\begin{array}{c}-1; \\ -2.\end{array}\right.\nonumber\]

Solo la\(+\) raíz satisface la condición inicial, por lo que la solución única a la oda y condición inicial es \[\label{eq:5} y=\frac{1}{2}[-3+\sqrt{1+4\sin 2x}].\]

Para determinar (i) los valores\(x > 0\) para los cuales existe la solución, requerimos\[1+4\sin 2x\geq 0,\nonumber\] o \[\label{eq:6}\sin 2x\geq -\frac{1}{4}.\]

Observe que en\(x = 0\), tenemos\(\sin 2x = 0\); en\(x = π/4\), tenemos\(\sin 2x = 1;\) en\(x = π/2\), tenemos\(\sin 2x = 0\); y en\(x = 3π/4\), tenemos\(\sin 2x = −1\). Por lo tanto, necesitamos determinar el valor de\(x\) tal que\(\sin 2x = −1/4\), con\(x\) en el rango\(π/2 < x < 3π/4\). La solución a la oda entonces existirá para todos\(x\) entre cero y este valor.

Para resolver\(\sin 2x = −1/4\) para\(x\) en el intervalo\(π/2 < x < 3π/4\), es necesario recordar la definición de\(\text{arcsin}\), o\(\sin^{−1}\), como se encuentra en una calculadora científica típica. El inverso de la función\[f(x)=\sin x,\quad -\pi /2\leq x\leq \pi /2\nonumber\] se denota por\(\text{arcsin}\). La primera solución con\(x > 0\) de la ecuación\(\sin 2x = −1/4\) coloca\(2x\) en el intervalo\((π, 3π/2)\), así que para invertir esta ecuación usando el\(\text{arcsine}\) necesitamos aplicar la identidad\(\sin (π − x) = \sin x\), y reescribir\(\sin 2x = −1/4\) como\(\sin (π − 2x) = −1/4\). La solución de esta ecuación se puede encontrar tomando el\(\text{arcsine}\), y es\[\pi -2x=\text{arcsin}(-1/4),\nonumber\] o\[x=\frac{1}{2}\left(\pi +\text{arcsin}\frac{1}{4}\right).\nonumber\]

Por lo tanto la solución existe para\(0 ≤ x ≤ (π + \text{arcsin} (1/4)) /2 = 1.6971\ldots\), donde hemos utilizado un valor de calculadora (computando en radianes) para encontrar\(\text{arcsin}(0.25) = 0.2527\ldots\). En el valor\((x, y) = (1.6971\ldots , −3/2)\), la curva de solución termina y\(dy/dx\) se vuelve infinita.

Para determinar (ii) el valor de\(x\) al cual\(y = y(x)\) es máximo, examinamos\(\eqref{eq:5}\) directamente. El valor de\(y\) será máximo cuando\(\sin 2x\) tome su valor máximo sobre el intervalo donde exista la solución. Esto será cuando\(2x = π/2\), o\(x = π/4 = 0.7854\ldots\).

El gráfico de\(y=y(x)\) se muestra en la Fig. 3.3.1.