2.6: Oscilaciones forzadas y resonancia

Consideremos el ejemplo de una masa en un manantial. Ahora examinamos el caso de las oscilaciones forzadas, que aún no manejamos. Es decir, consideramos la ecuación

\[ mx'' + cx' + kx = F(t) \nonumber \]

para algunos que no sean cero\(F(t) \). La configuración es otra vez:\(m\) es masa,\(c\) es fricción,\(k\) es la constante del resorte, y\(F(t)\) es una fuerza externa que actúa sobre la masa.

Figura\(\PageIndex{1}\)

Lo que nos interesa es el forzamiento periódico, como las partes giratorias no centradas, o quizás los sonidos fuertes, u otras fuentes de fuerza periódica. Una vez que aprendamos sobre las series de Fourier en el Capítulo 4, veremos que cubrimos todas las funciones periódicas simplemente considerando\(F(t) = F_0 \cos (\omega t)\) (o seno en lugar de coseno, los cálculos son esencialmente los mismos).

Movimiento Forzado y Resonancia Sin Amortiguar

Primero consideremos el\(c = 0\) movimiento sin amortiguar por simplicidad. Tenemos la ecuación

\[ mx'' + kx = F_0 \cos (\omega t) \nonumber \]

Esta ecuación tiene la solución complementaria (solución a la ecuación homogénea asociada)

\[x_c = C_1 \cos ( \omega_0t) + C_2 \sin (\omega_0t) \nonumber \]

donde\(\omega_0 = \sqrt { \frac {k}{m}}\) está la frecuencia natural (angular), que es la frecuencia a la que el sistema “quiere oscilar” sin interferencia externa.

Supongamos eso\(\omega_0 \neq \omega \). Intentamos la solución\(x_p = A \cos (\omega t) \) y resolvemos para\(A\). Tenga en cuenta que no necesitamos tener seno en nuestra solución de prueba ya que en el lado izquierdo solo obtendremos cosenos de todos modos. Si incluyes un seno está bien; encontrarás que su coeficiente será cero.

Resolvemos usando el método de coeficientes indeterminados. Encontramos que

\[x_p = \dfrac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber \]

Lo dejamos como un ejercicio para hacer el álgebra requerida.

La solución general es

\[ x = C_1 \cos (\omega_0t) + C_2 \sin (\omega_0t) + \frac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber \]

o escrito de otra manera

\[ x = C \cos (\omega_0t - y ) + \frac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber \]

De ahí que se trate de una superposición de dos ondas coseno a diferentes frecuencias.

Ejemplo\(\PageIndex{1}\)

Toma

\[ 0.5 x'' + 8 x = 10 \cos (\pi t), \quad x(0) = 0, \quad x' (0) = 0 \nonumber \]

Vamos a calcular. Primero leemos los parámetros:\( \omega = \pi, \omega_0 = \sqrt { \frac {8}{0.5}} = 4, F_0 = 10, m = 0.5 \). La solución general es

\[ x = C_1 \cos (4t) + C_2 \sin (4t) + \frac {20}{16 - {\pi }^2} \cos ( \pi t) \nonumber \]

Resolver\(C_1\) y\(C_2\) usar las condiciones iniciales. Es fácil ver eso\( C_1 = \frac {-20}{16 - {\pi}^2}\) y\( C_2 = 0 \). De ahí

\[ x = \frac {20}{16 - {\pi}^2} ( \cos (\pi t) - \cos ( 4t ) ) \nonumber \]

Figura\(\PageIndex{2}\): Gráfica de\( \frac {20}{16 - {\pi}^2} ( \cos ( \pi t) - \cos ( 4t )) \).

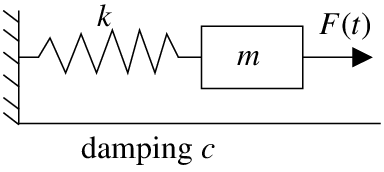
Observe el comportamiento de “golpiza” en la Figura\(\PageIndex{2}\). Primer uso de la identidad trigonométrica

\[ 2 \sin ( \frac {A - B}{2}) \sin ( \frac {A + B}{2} ) = \cos B - \cos A \nonumber \]

para conseguir que

\[ x = \frac {20}{16 - {\pi}^2} ( 2 \sin ( \frac {4 - \pi}{2}t) \sin ( \frac {4 + \pi}{2} t)) \nonumber \]

Observe que\(x\) es una onda de alta frecuencia modulada por una onda de baja frecuencia.

Ahora supongamos eso\( \omega_0 = \omega \). Obviamente, no podemos probar la solución\( A \cos (\omega t) \) y luego usar el método de coeficientes indeterminados. Notamos que\( \cos (\omega t) \) resuelve la ecuación homogénea asociada. Por lo tanto, tenemos que intentarlo\( x_p = At \cos (\omega t) + Bt \sin (\omega t) \). Esta vez sí necesitamos el término seno ya que la segunda derivada de\( t \cos (\omega t) \) sí contiene senos. Escribimos la ecuación

\[ x'' + \omega^2 x = \frac {F_0}{m} \cos (\omega t) \nonumber \]

Al\( x_p\) enchufarse en el lado izquierdo obtenemos

\[ 2B \omega \cos (\omega t) - 2A \omega \sin (\omega t) = \frac {F_0}{m} \cos (\omega t) \nonumber \]

De ahí\( A = 0 \) y\( B = \frac {F_0}{2m \omega } \). Nuestra solución particular es\( \frac {F_0}{2m \omega } t \sin (\omega t) \) y nuestra solución general es

\[ x = C_1 \cos (\omega t) + C_2 \sin (\omega t) + \frac {F_0}{2m \omega } t \sin (\omega t) \nonumber \]

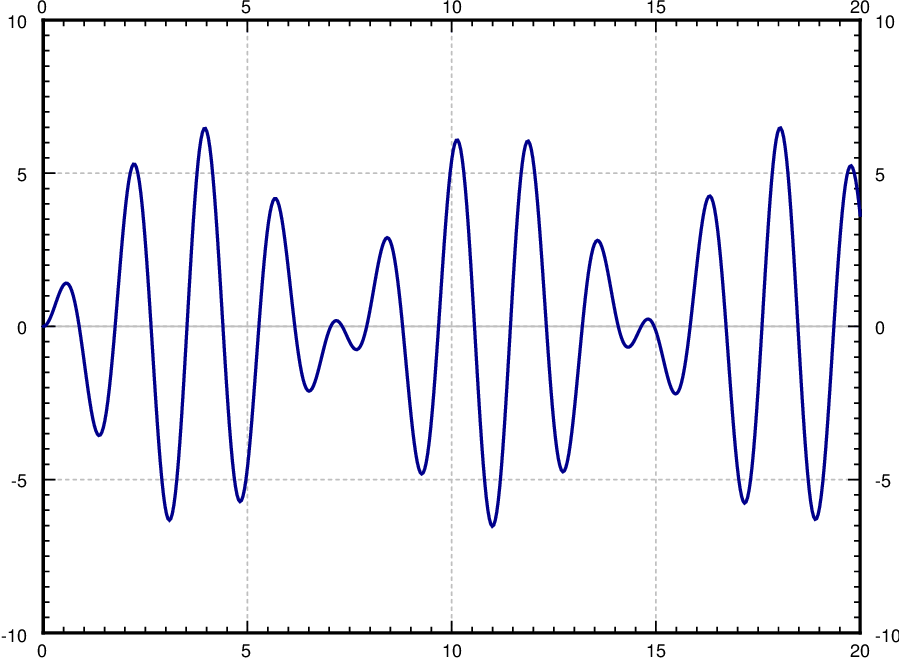
El término importante es el último (la solución particular que encontramos). Podemos ver que este término crece sin ataduras como\( t \rightarrow \infty \). De hecho oscila entre\( \frac {F_0t}{2m \omega } \) y\( \frac {-F_0t}{2m \omega } \). Los dos primeros términos solo oscilan entre ellos\( \pm \sqrt { C^2_1 + C^2_2} \), lo que se hace cada vez más pequeño en proporción a las oscilaciones del último término a medida que\(t\) se hace más grande. En la Figura\(\PageIndex{3}\) vemos la gráfica con\(C_1 = C_2 = 0, F_0 = 2, m = 1, \omega = \pi \).

Figura\(\PageIndex{3}\): Gráfica de\(\frac{1}{\pi}t\sin (\pi t)\).

Al forzar al sistema en la frecuencia justa producimos oscilaciones muy salvajes. Este tipo de comportamiento se llama resonancia o tal vez resonancia pura. A veces se desea resonancia. Por ejemplo, ¿recuerdas cuando de niño podrías empezar a balancearte simplemente moviéndote hacia adelante y hacia atrás en el columpio en la “frecuencia correcta”? Estabas tratando de lograr resonancia. La fuerza de cada uno de tus movimientos era pequeña, pero al cabo de un tiempo produjo grandes oscilaciones.

Por otro lado la resonancia puede ser destructiva. En un sismo algunos edificios colapsan mientras que otros pueden estar relativamente intactos. Esto se debe a que diferentes edificios tienen diferentes frecuencias de resonancia. Por lo que averiguar la frecuencia de resonancia puede ser muy importante.

Un ejemplo común (pero erróneo) de fuerza destructiva de resonancia es la falla del puente Tacoma Narrows. Resulta que hubo un fenómeno diferente en juego. \(^{1}\)

Movimiento forzado amortiguado y resonancia práctica

En la vida real las cosas no son tan simples como lo fueron arriba. Hay, por supuesto, algo de amortiguamiento. Nuestra ecuación se convierte en

\[ \label{eq:15} mx'' + cx' + kx = F_0 \cos (\omega t), \]

para algunos\( c > 0 \). Ya hemos resuelto el problema homogéneo antes. Dejamos

\[ p = \frac {c}{2m}\quad \omega_0 = \sqrt { \frac {k}{m} } \nonumber \]

Reemplazamos la ecuación\(\eqref{eq:15}\) con

\[ x'' + 2px' + \omega^2_0x = \frac {F_0}{m} \cos (\omega t) \nonumber \]

Las raíces de la ecuación característica del problema homogéneo asociado son\(r_1, r_2 = -p \pm \sqrt {p^2 - \omega_0^2} \). La forma de la solución general de la ecuación homogénea asociada depende del signo de\( p^2 - \omega^2_0 \), o equivalentemente del signo de\( c^2 - 4km \), como hemos visto antes. Es decir,

\[ x_c = \begin {cases} C_1e^{r_1t} + C_2e^{r_2t}, & \text{if }c^2 > 4km, \\ C_1e^{pt} + C_2te^{-pt}, & \text{if }c^2 = 4km, \\ e^{-pt} ( C_1 \cos (\omega_1t) + C_2 \sin (\omega_1t)), & \text{if }c^2 < 4km, \end {cases} \nonumber \]

donde\( \omega_1 = \sqrt {\omega^2_0 - p^2 } \). En cualquier caso, podemos verlo\( x_c(t) \rightarrow 0 \) como\( t \rightarrow \infty \). Además, no puede haber conflictos a la hora de intentar resolver los coeficientes indeterminados mediante el intento\( x_p = A \cos (\omega t) + B \sin (\omega t) \). Vamos a enchufar y resolver para\( A\) y\(B\). Obtenemos (los tediosos detalles se dejan al lector)

\[ ((\omega^2_0 - \omega^2) B - 2 \omega pA ) \sin (\omega t) + ((\omega^2_0 - \omega^2) A + 2 \omega pB ) \cos (\omega t) = \frac {F_0}{m} \cos (\omega t) \nonumber \]

Lo conseguimos

\[ A = \frac { (\omega^2_0 - \omega^2) F_0}{m{(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \nonumber \]

\[ B = \frac { 2 \omega pF_0}{m{(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \nonumber \]

También calculamos\( C = \sqrt { A^2 + B^2} \) para ser

\[ C = \frac {F_0}{m \sqrt { {(2 \omega p)}^2 + {(\omega^2_0 - \omega^2)}^2}} \nonumber \]

Por lo tanto, nuestra solución particular es

\[ x_P = \frac {(\omega^2_0 - \omega^2)F_0}{m {(2 \omega p)}^2 + m {(\omega^2_0 - \omega^2)}^2} \cos (\omega t) + \frac {2 \omega pF_0}{m {(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \sin (\omega t) \nonumber \]

O en la notación alternativa tenemos amplitud\( C\) y desplazamiento de fase\( \gamma \) donde (si\( \omega \ne \omega_0 \))

\[ \tan \gamma = \frac {B}{A} = \frac {2 \omega p}{\omega^2_0 - \omega^2} \nonumber \]

De ahí que tengamos

\[ x_p = \frac {F_0}{m \sqrt { {(2 \omega p)}^2 + {(\omega^2_0 - \omega ^2)}^2}} \cos (\omega t - \gamma) \nonumber \]

Si\( \omega = \omega_0\) vemos eso\( A = 0, B = C = \frac {F_0}{2m \omega p}, ~\rm{and} ~ \gamma = \frac {\pi}{2} \).

La fórmula exacta no es tan importante como la idea. No memorices la fórmula anterior, en cambio debes recordar las ideas involucradas. Para diferentes funciones de forzamiento\( F\), obtendrás una fórmula diferente para\( x_p\). Por lo que no tiene sentido memorizar esta fórmula específica. Siempre puedes volver a calcularlo más tarde o buscarlo si realmente lo necesitas.

Por razones vamos a explicar en un momento, llamamos a\(x_c\) la solución transitoria y la denotamos por\( x_{tr} \). Llamamos al\( x_p\) que encontramos por encima de la solución periódica constante y la denotamos por\( x_{sp}\). La solución general a nuestro problema es

\[ x = x_c + x_p = x_{tr} + x_ {sp} \nonumber \]

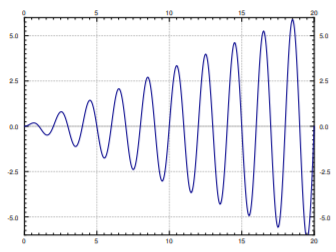
Observamos que\( x_c = x_{tr} \) va a cero ya que\( t \rightarrow \infty \), ya que todos los términos implican un exponencial con un exponente negativo. De ahí que para grandes\(t\), el efecto de\( x_{tr} \) sea insignificante y esencialmente solo veremos\(x_{sp}\). De ahí el nombre transitorio. Observe que no\( x_{sp}\) implica constantes arbitrarias, y las condiciones iniciales sólo afectarán\(x_{tr} \). Esto significa que el efecto de las condiciones iniciales será insignificante después de algún periodo de tiempo. Debido a este comportamiento, también podríamos enfocarnos en la solución periódica constante e ignorar la solución transitoria. Ver Figura\(\PageIndex{4}\) para una gráfica de diferentes condiciones iniciales.

Figura\(\PageIndex{4}\): Soluciones con diferentes condiciones iniciales para parámetros\( k = 1, m = 1, F_0 = 1, c = 0.7,\) y\( \omega = 1.1. \)

Observe que la velocidad a la que\(x_{tr}\) va a cero depende de\(P\) (y por lo tanto\(c\)). Cuanto más grande\(P\) es (cuanto más grande\(c\) es), el “más rápido”\(x_{tr}\) se vuelve insignificante. Entonces, cuanto menor sea la amortiguación, más larga será la “región transitoria”. Esto concuerda con la observación de que cuando\( c = 0 \), las condiciones iniciales afectan el comportamiento para todos los tiempos (es decir, una “región transitoria” infinita).

Describamos lo que entendemos por resonancia cuando hay amortiguamiento presente. Al no haber conflictos a la hora de resolver con coeficiente indeterminado, no hay término que vaya al infinito. Lo que veremos sin embargo es el valor máximo de la amplitud de la solución periódica constante. Dejar\(C\) ser la amplitud de\(x_{sp}\). Si\(C\) trazamos en función de\(\omega \) (con todos los demás parámetros fijos) podemos encontrar su máximo. Llamamos al\(\omega \) que logra este máximo la frecuencia de resonancia práctica. Llamamos a la amplitud máxima\(C(\omega )\) la amplitud práctica de resonancia. Así, cuando el amortiguamiento está presente se habla de resonancia práctica más que de resonancia pura. En la Figura se da una gráfica de\(c\) muestra para tres valores diferentes de\(\PageIndex{5}\). Como puede ver la amplitud práctica de la resonancia crece a medida que la amortiguación se hace más pequeña, y cualquier resonancia práctica puede desaparecer cuando la amortiguación es grande.

Figura\(\PageIndex{5}\): Gráfica\(C( \omega )\) de resonancia práctica con parámetros\( k = 1, m =1, F_0 = 1 \). The top line is with \(c = 0.4 \), the middle line with \( c = 0.8 \), and the bottom line with \( c = 1.6 \).

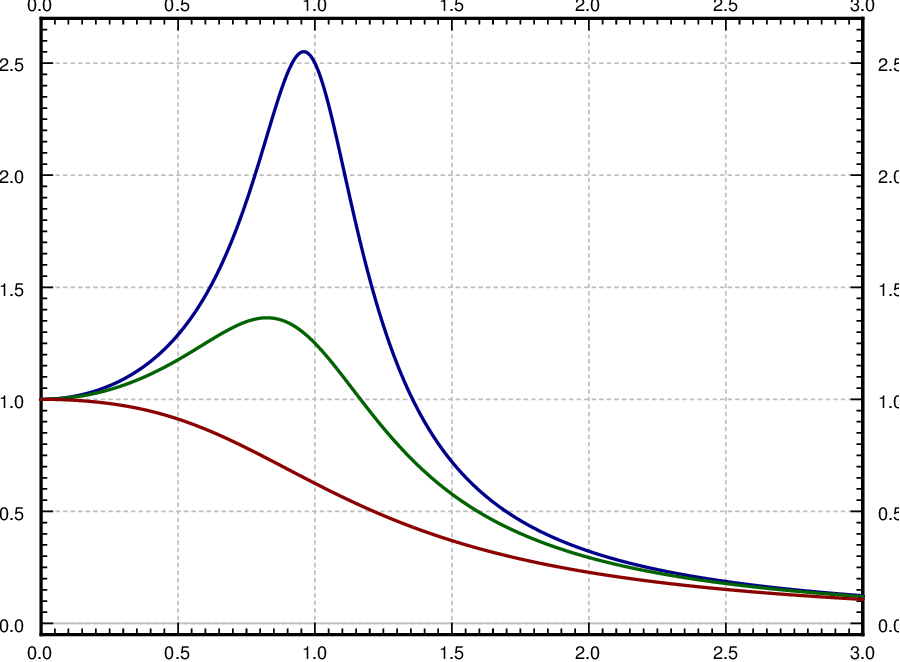
Para encontrar el máximo necesitamos encontrar el derivado\( C' (\omega ) \). Espectáculos de cómputos

\[ C' (\omega ) = \frac {-4 \omega (2p^2 + \omega^2 - \omega^2_0)F_0}{m {( {(2 \omega p)}^2 + {(\omega^2_0 - \omega^2)})}^{3/2}} \nonumber \]

Esto es cero ya sea cuando\( \omega = 0 \) o cuando\( 2p^2 + \omega^2 - \omega^2_0 = 0 \). En otras palabras,\( C' (\omega ) = 0 \) cuando

\[ \omega = \sqrt { \omega^2_0 - 2p^2} \rm{~or~} \omega = 0 \nonumber \]

Se puede demostrar que si\( \omega^2_0 - 2p^2 \) es positivo, entonces\( \sqrt {\omega^2_0 - 2p^2} \) es la frecuencia de resonancia práctica (ese es el punto donde\( C(\omega ) \) es máxima, nótese que en este caso\( C' (\omega ) > 0 \) para pequeños\(\omega \)). Si\(\omega = 0 \) es el máximo, entonces esencialmente no hay resonancia práctica ya que suponemos que\( \omega > 0 \) en nuestro sistema. En este caso la amplitud se hace mayor a medida que la frecuencia de forzamiento se hace menor.

Si se produce resonancia práctica, la frecuencia es menor que\( \omega_0\). A medida que la amortiguación\(c\) (y por lo tanto\(P\)) se vuelve más pequeña, la frecuencia de resonancia práctica va a\( \omega_0\). Entonces cuando la amortiguación es muy pequeña,\( \omega_0\) es una buena estimación de la frecuencia de resonancia. Este comportamiento concuerda con la observación de que cuando\( c = 0 \), entonces\( \omega_0\) es la frecuencia de resonancia.

Otra observación interesante que hacer es que cuando\(\omega\to\infty\), entonces\(\omega\to 0\). Esto significa que si la frecuencia de forzamiento es demasiado alta no logra que la masa se mueva en el sistema masa-resorte. Esto es bastante razonable de manera intuitiva. Si nos movemos de un lado a otro muy rápido mientras estamos sentados en un columpio, no vamos a conseguir que se mueva en absoluto, no importa cuán contundente sea. Las vibraciones rápidas simplemente se cancelan entre sí antes de que la masa tenga alguna posibilidad de responder moviéndose de una manera u otra.

El comportamiento es más complicado si la función de forzamiento no es una onda coseno exacta, sino por ejemplo una onda cuadrada. Una función periódica general será la suma (superposición) de muchas ondas coseno de diferentes frecuencias. Se anima al lector a volver a esta sección una vez que hayamos aprendido sobre la serie de Fourier.

Notas al pie

¹ K. Billah y R. Scanlan, Resonancia, Tacoma Narrows Bridge Failure, y libros de texto de licenciatura en física, American Journal of Physics, 59 (2), 1991, 118—124, http://www.ketchum.org/billah/Billah-Scanlan.pdf