4.1: Problemas de valor límite

Antes de abordar la serie de Fourier, necesitamos estudiar los llamados problemas de valor límite (o problemas de punto final). Por ejemplo, supongamos que tenemos

\[ x'' + \lambda x = 0,\quad x(a)=0, \quad x(b)=0, \nonumber \]

para alguna constante\( \lambda\), donde\( x(t)\) se define para\(t\) en el intervalo\([a,b]\). A diferencia de antes, cuando especificamos el valor de la solución y su derivada en un solo punto, ahora especificamos el valor de la solución en dos puntos diferentes. Obsérvese que\( x=0\) es una solución a esta ecuación, por lo que la existencia de soluciones no es un problema aquí. La singularidad de las soluciones es otro tema. La solución general a\( x''+\lambda x = 0\) tiene dos constantes arbitrarias presentes. \(^{1}\)Es, por tanto, natural (pero erróneo) creer que exigir dos condiciones garantiza una solución única.

Ejemplo\(\PageIndex{1}\)

Tomar\( \lambda = 1, a=0, b=\pi\). Es decir,

\[ x''+x=0, \quad x(0)=0, \quad x(\pi)=0. \nonumber \]

Entonces\( x= \sin t\) es otra solución (además\(x=0\)) que satisface ambas condiciones de contorno. Hay más. Anote la solución general de la ecuación diferencial, que es\( x=A \cos t+B \sin t\). Las\( x(0)=0\) fuerzas de condición\(A=0\). Dejar\(x(\pi)=0\) no nos da más información\( x=B \sin t\) ya que ya satisface ambas condiciones de contorno. De ahí que haya infinitamente muchas soluciones de la forma\(x= B \sin t\), donde\(B\) es una constante arbitraria.

Ejemplo\(\PageIndex{2}\)

Por otro lado, cambiar a\(\lambda =2\).

\[ x''+2x=0, \quad x(0)=0, \quad x(\pi)=0. \nonumber \]

Entonces la solución general es\(x=A \cos(\sqrt2 t)+B \sin(\sqrt2 t)\). Dejando\(x(0)=0\) fuerzas inmóviles\(A=0\). Aplicamos la segunda condición para encontrar\( 0=x(\pi)=B \sin(\sqrt2 t)\). A medida\( \sin(\sqrt2 t) \neq 0\) que obtengamos\(B=0\). Por lo tanto,\(x=0\) es la solución única a este problema.

¿Qué está pasando? Estaremos interesados en encontrar qué constantes\(\lambda\) permiten una solución distinta de cero, y nos interesará encontrar esas soluciones. Este problema es un análogo de encontrar valores propios y vectores propios de matrices.

Problemas de autovalor

Para la teoría básica de series de Fourier necesitaremos los siguientes tres problemas de valores propios. Consideraremos ecuaciones más generales, pero pospondremos esto hasta el Capítulo 5.

\[\begin{align} \label{eq:4} & x''+ \lambda x=0, & x(a)=0, \quad & x(b)=0, \\ \label{eq:5} & x''+ \lambda x=0, & x'(a)=0, \quad & x'(b)=0, \end{align} \]

y

\[ \label{eq:6} x''+ \lambda x=0,~~~ x(a)=x(b), ~~~x'(a)=x'(b), \]

Un número\(\lambda\) se llama un valor propio de\(\eqref{eq:4}\) (resp. \(\eqref{eq:5}\)o\(\eqref{eq:6}\)) si y solo si existe una solución distinta de cero (no idénticamente cero) a\(\eqref{eq:4}\) (resp. \(\eqref{eq:5}\)o\(\eqref{eq:6}\)) dado ese específico\(\lambda\). La solución distinta de cero que encontramos se llama la función propia correspondiente.

Obsérvese la similitud con los valores propios y los vectores propios de las matrices. La similitud no es sólo una coincidencia. Si pensamos en las ecuaciones como operadores diferenciales, entonces estamos haciendo exactamente lo mismo. Piense en una función\(x(t)\) como un vector con infinitamente muchos componentes (uno para cada uno\(t\)). Dejar\(L = -\frac{d^2}{{dt}^2}\) ser el operador lineal. Entonces el par autovalor/función propia debería ser\(\lambda\) y distinto de cero\(x\) tal que\(Lx = \lambda x\). En otras palabras, estamos buscando funciones distintas de cero que\(x\) satisfagan ciertas condiciones de punto final que resuelvan\((L- \lambda)x = 0\). Mucho del formalismo del álgebra lineal todavía se aplica aquí, aunque no vamos a seguir esta línea de razonamiento demasiado lejos.

Ejemplo\(\PageIndex{3}\)

Encontremos los valores propios y las funciones propias de

\[ x''+ \lambda x=0,\quad x(0)=0, \quad x(\pi)=0. \nonumber \]

Por razones que quedarán claras a partir de los cómputos, tendremos que manejar los casos\(\lambda > 0, \lambda=0, \lambda<0\) por separado. Primero supongamos que\(\lambda > 0\), luego la solución general a\( x''+ \lambda x=0\) es

\[ x=A \cos(\sqrt{\lambda}t)+B \sin(\sqrt{\lambda}t). \nonumber \]

La condición\( x(0)=0\) implica de inmediato\(A \). Siguiente

\[ 0=x(\pi)=B \sin(\sqrt{\lambda} \pi). \nonumber \]

Si\(B\) es cero, entonces no\(x\) es una solución distinta de cero. Entonces, para conseguir una solución distinta de cero debemos tener eso\( \sin( \sqrt{\lambda} \pi)=0\). Por lo tanto,\( \sqrt{\lambda} \pi\) debe ser un múltiplo entero de\(\pi\). En otras palabras,\(\sqrt{\lambda}=k \) para un entero positivo\(k\). De ahí que los valores propios positivos sean\(k^2\) para todos los enteros\(k \geq 1 \). Las funciones propias correspondientes se pueden tomar como\( x =\sin(kt)\). Al igual que para los vectores propios, obtenemos todos los múltiplos de una función propia, así que solo necesitamos elegir uno.

Ahora supongamos eso\(\lambda=0\). En este caso la ecuación es\( x''=0\) y la solución general es\( x=At+B\). La condición\(x(0)=0\) implica eso\( B=0\), e\( x(\pi)=0\) implica eso\( A=0\). Esto quiere decir que no\( \lambda = 0\) es un valor propio.

Por último, supongamos que\( \lambda <0\). En este caso tenemos la solución general \(^{2}\)

\[ x= A \cosh( \sqrt{- \lambda}t) +B \sinh( \sqrt{- \lambda} t). \nonumber \]

Dejar\(x(0)=0\) implica eso\(A=0\) (recordar\( \cosh0 =1\) y\( \sinh0=0\)). Entonces nuestra solución debe ser\( x=B \sinh(\sqrt{- \lambda} t)\) y satisfacer\(x(\pi)=0\). Esto sólo es posible si\(B\) es cero. ¿Por qué? Porque sólo\(\sinh \xi\) es cero cuando\(\xi=0\). Deberías\(\sinh\) tramar para ver este hecho. Esto también lo podemos ver desde la definición de sinh. Obtenemos\( 0 = \sinh t = \frac{e^t-e^{-t}}{2}\). De ahí\(e^t=e^{-t}\), lo que implica\(t=-t\) y eso sólo es cierto si\(t=0\). Por lo que no hay valores propios negativos.

En resumen, los valores propios y las funciones propias correspondientes son

\[ \lambda_k = k^2\quad\text{with an eigenfucntion}\quad x_k=\sin(kt) \quad\text{for all integers } k \geq 1. \nonumber \]

Ejemplo\(\PageIndex{4}\)

Vamos a calcular los valores propios y las funciones propias de

\[ x''+ \lambda x=0,~~~ x'(0)=0,~~~x'(\pi)=0. \nonumber \]

Nuevamente tendremos que manejar los casos\( \lambda > 0, \lambda=0, \lambda<0\) por separado. Primero supongamos eso\( \lambda > 0\). La solución general a\( x'' + \lambda x=0\) es\( x=A \cos(\sqrt{\lambda}t)+ B \sin(\sqrt{\lambda}t)\). Entonces

\[ x'=-A \sqrt{\lambda } \sin(\sqrt{\lambda }t)+B \sqrt{\lambda } \cos(\sqrt{\lambda }t). \nonumber \]

La condición\( x'(0)=0\) implica de inmediato\( B=0\). Siguiente

\[ 0=x'(\pi)=-A \sqrt{\lambda} \sin(\sqrt{\lambda} \pi). \nonumber \]

De nuevo\( A\) no puede ser cero si\( \lambda\) va a ser un valor propio, y\(\sin(\sqrt{\lambda} \pi)\) es solo cero si es\(\sqrt{\lambda}=k \) para un entero positivo\(k\). De ahí que los valores propios positivos vuelvan a ser\(k^2\) para todos los enteros\(k \geq 1\). Y las funciones propias correspondientes se pueden tomar como\( x= \cos(kt)\).

Ahora supongamos eso\( \lambda = 0\). En este caso la ecuación es\( x''=0\) y la solución general es\( x=At +B\) así\(x'=A\). La condición\(x'(0)=0\) implica eso\(A=0\). Ahora\(x'(\pi)=0\) también simplemente implica\(A=0\). Esto quiere decir que\(B\) podría ser cualquier cosa (tomémoslo como 1). Así\(\lambda = 0\) es un valor propio y\(x=1\) es una función propia correspondiente.

Por último, vamos\( \lambda < 0\). En este caso tenemos la solución general\( x=A \cosh(\sqrt{ - \lambda}t)+B \sinh(\sqrt{ - \lambda}t)\) y por lo tanto

\[ x' = A \sqrt{-\lambda} \sinh(\sqrt{ - \lambda}t) + B \sqrt{-\lambda} \cosh(\sqrt{ - \lambda}t). \nonumber \]

Ya hemos visto (con roles de\(A\) y\(B\) cambiados) que para que esto sea cero en\(t=0\) e\(t= \pi\) implica eso\( A=B=0\). De ahí que no haya valores propios negativos.

En resumen, los valores propios y las funciones propias correspondientes son

\[ \lambda_k = k^2\quad\text{with an eigenfunction}\quad x_k=\cos(kt) \quad\text{for all integers } k \geq 1, \nonumber \]

y hay otro valor propio

\[ \lambda_0 = 0\quad\text{with an eigenfunction}\quad x_0= 1. \nonumber \]

El siguiente problema es el que lleva a la serie general de Fourier.

Ejemplo\(\PageIndex{5}\)

Vamos a calcular los valores propios y las funciones propias de

\[ x''+ \lambda x=0,~~~~x(- \pi)=x(\pi),~~~~x'(- \pi)=x'(\pi). \nonumber \]

Observe que no hemos especificado los valores o las derivadas en los puntos finales, sino que son los mismos al principio y al final del intervalo.

Vamos a saltarnos\( \lambda < 0\). Los cálculos son los mismos que antes, y nuevamente encontramos que no hay valores propios negativos.

Para\( \lambda =0\), la solución general es\( x=At + B\). La condición\( x(- \pi)=x(\pi)\) implica que eso\( A=0 \)\( ( A \pi +B=-A \pi+B\) implica\(A=0)\). La segunda condición no\( x'(- \pi)=x'( \pi)\) dice nada sobre\(B\) y por lo tanto\( \lambda = 0\) es un valor propio con una función propia correspondiente\( x=1\).

Porque eso\( \lambda >0\) lo conseguimos\( x = A \cos(\sqrt{ \lambda}t) + B \sin(\sqrt{ \lambda}t) \). Ahora

\[\underbrace{A \cos (-\sqrt{\lambda}\, \pi) + B \sin (-\sqrt{\lambda}\, \pi)}_{x(-\pi)} = \underbrace{A \cos ( \sqrt{\lambda}\, \pi ) + B \sin ( \sqrt{\lambda}\, \pi)}_{x(\pi)} . \nonumber \]

Eso lo recordamos\( \cos(- \theta)=\cos( \theta)\) y\( \sin(- \theta)= - \sin( \theta)\). Por lo tanto,

\[ A \cos( \sqrt{\lambda} \pi)- B \sin( \sqrt{\lambda} \pi) = A \cos( \sqrt{\lambda} \pi)+ B \sin( \sqrt{\lambda} \pi). \nonumber \]

De ahí ya sea\( B=0\) o\( \sin(\sqrt{\lambda} \pi)=0\). De igual manera (ejercicio) si diferenciamos\(x\) y enchufamos la segunda condición nos encontramos con que\( A=0\) o\( \sin(\sqrt{\lambda} \pi)=0\). Por lo tanto,\(B\) a menos que queramos\(A\) y para que ambos sean cero (lo cual no lo hacemos) debemos tener\( \sin(\sqrt{\lambda} \pi)=0\). Por lo tanto,\( \sqrt{\lambda}\) es un número entero y los valores propios son una vez más\( \lambda = k^2\) para un entero\( k \geq 1\). En este caso, sin embargo,\( x=A \cos(kt)+ B \sin(kt)\) es una función propia para cualquiera\( A\) y cualquiera\(B\). Entonces tenemos dos funciones propias linealmente independientes\(\sin(kt)\) y\(\cos(kt)\). Recuerde que para una matriz también podríamos haber tenido dos vectores propios correspondientes a un solo valor propio si se repitió el valor propio.

En resumen, los valores propios y las funciones propias correspondientes son

\[\begin{align}\begin{aligned} & \lambda_k = k^2 & & \text{with eigenfunctions} & & \cos (k t) \quad \text{and}\quad \sin (k t) & & \text{for all integers } k \geq 1 , \\ & \lambda_0 = 0 & & \text{with an eigenfunction} & & x_0 = 1.\end{aligned}\end{align} \nonumber \]

Ortogonalidad de las funciones propias

Algo que será muy útil en la siguiente sección es la propiedad de ortogonalidad de las funciones propias. Este es un análogo del siguiente hecho sobre los vectores propios de una matriz. Una matriz se llama simétrica if\(A=A^T\). Los vectores propios para dos valores propios distintos de una matriz simétrica son ortogonales. Esa simetría se requiere. Aquí no vamos a probar este hecho. Los operadores diferenciales con los que estamos tratando actúan como una matriz simétrica. Nosotros, por lo tanto, obtenemos el siguiente teorema.

Teorema\(\PageIndex{1}\): Orthogonal

S uppose eso\( x_1(t)\) y\( x_2(t)\) son dos funciones propias del problema\(\eqref{eq:4}\),\(\eqref{eq:5}\) o\(\eqref{eq:6}\) para dos autovalores diferentes\(\lambda_1\) y\(\lambda_2\). Entonces son ortogonales en el sentido de que

\[ \int^b_a x_1(t)x_2(t)dt=0. \nonumber \]

Tenga en cuenta que la terminología proviene del hecho de que la integral es un tipo de producto interno. Ampliaremos sobre esto en la siguiente sección. El teorema tiene una prueba muy corta, elegante e iluminadora así que démosla aquí. Primero tenga en cuenta que tenemos las siguientes dos ecuaciones.

\[ x''_1 +\lambda_1x_1=0~~~~ {\rm{and}}~~~~ x''_2+\lambda_2x_2 = 0. \nonumber \]

Multiplicar el primero por\( x_2\) y el segundo por\( x_1\) y restar para obtener

\[ (\lambda_1- \lambda_2)x_1x_2=x''_2x_1-x_2x''_1. \nonumber \]

Ahora integre ambos lados de la ecuación.

\[\begin{align}\begin{aligned} (\lambda_1- \lambda_2) \int^b_a x_1x_2dt &=\int^b_a x''_2x_1-x_2x''_1dt \\ &= \int^b_a \frac{d}{dt} (x'_2x_1-x_2x'_1)dt \\ &= [ x'_2x_1-x_2x'_1]^b_{t=a} = 0.\end{aligned}\end{align} \nonumber \]

La última igualdad se mantiene por las condiciones de límite. Por ejemplo, si consideramos\(\eqref{eq:4}\) que tenemos\( x_1(a)=x_1(b)=x_2(a)=x_2(b)=0\) y así\( x'_2x_1-x_2x'_1\) es cero en ambos\(a\) y\(b\). Como\( \lambda_1 \neq \lambda_2\) sigue el teorema.

Ejercicio\(\PageIndex{1}\): (easy)

Terminar el teorema (verificar la última igualdad en la prueba) para los casos\(\eqref{eq:5}\) y\(\eqref{eq:6}\).

Hemos visto anteriormente que\( \sin(nt)\) era una función propia para el problema\( x''+ \lambda x=0,\: x(0)=0,\: x(\pi)=0\). De ahí que tengamos la integral

\[\int_{0}^\pi \sin (mt) \sin (nt) \,dt = 0 , \quad \text{when } m \not = n. \nonumber \]

Del mismo modo,\[\int_{0}^\pi \cos (mt) \cos (nt) \,dt = 0 , \quad \text{when } m \not = n, \qquad \text{and} \qquad \int_{0}^\pi \cos (nt) \,dt = 0 . \nonumber \]

Y finalmente también conseguimos

\[\int_{-\pi}^\pi \sin (mt) \sin (nt) \,dt = 0 , \quad \text{when } m \not = n, \qquad \text{and} \qquad \int_{-\pi}^\pi \sin (nt) \,dt = 0 , \nonumber \]\[\int_{-\pi}^\pi \cos (mt) \cos (nt) \,dt = 0 , \quad \text{when } m \not = n, \qquad \text{and} \qquad \int_{-\pi}^\pi \cos (nt) \,dt = 0 , \nonumber \]

y\[\int_{-\pi}^\pi \cos (mt) \sin (nt) \,dt = 0 \qquad \text{(even if $m=n$).} \nonumber \]

Fredholm Alternativa

Ahora tocamos un teorema muy útil en la teoría de ecuaciones diferenciales. El teorema se sostiene en un entorno más general de lo que vamos a decirlo, pero para nuestros fines es suficiente la siguiente afirmación. Daremos una versión un poco más general en el Capítulo 5.

Teorema\(\PageIndex{2}\)

Fredholm alternativas\(^{3}\)

Exactamente una de las siguientes declaraciones sostiene. O

\[ x'' + \lambda x=0,~~~~x(a)=0,~~~~x(b)=0 \nonumber \]

tiene una solución distinta de cero, o

\[\label{eq:32} x'' + \lambda x=f(t),~~~~x(a)=0,~~~~x(b)=0 \]

tiene una solución única para cada función\(f\) continua\([a,b]\).

El teorema también es cierto para los otros tipos de condiciones límite que consideramos. El teorema significa que si no\( \lambda\) es un valor propio, la ecuación no homogénea\(\eqref{eq:32}\) tiene una solución única para cada lado derecho. Por otro lado si\( \lambda\) es un valor propio, entonces no es\(\eqref{eq:32}\) necesario tener una solución para cada uno\(f\), y además, aunque pase a tener una solución, la solución no es única.

También queremos reforzar aquí la idea de que los operadores diferenciales lineales tienen mucho en común con las matrices. Por lo que no es de sorprender que también exista una versión dimensional finita de la alternativa de Fredholm para matrices. \(A\)Déjese ser una\(n \times n\) matriz. La alternativa de Fredholm afirma entonces que o bien\( (A- \lambda I) \vec{x}= \vec{0}\) tiene una solución no trivial, o\( (A- \lambda I) \vec{x}= \vec{b}\) tiene una solución para cada uno\( \vec{b}\).

Mucha intuición del álgebra lineal se puede aplicar a los operadores diferenciales lineales, pero hay que tener cuidado por supuesto. Por ejemplo, una diferencia que ya hemos visto es que en general un operador diferencial tendrá infinitamente muchos autovalores, mientras que una matriz sólo tiene finitamente muchos.

Aplicación

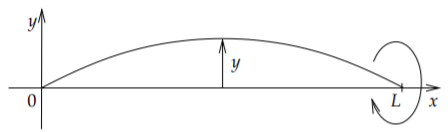
Consideremos una aplicación física de un problema de punto final. Supongamos que tenemos una cuerda elástica apretada que gira rápidamente o cuerda de densidad lineal uniforme\( \rho\). Pongamos este problema en el\(xy-\) avión. El\(x\) eje representa la posición en la cadena. La cuerda gira a velocidad angular\( \omega\), por lo que asumiremos que todo el\(xy-\) plano gira a velocidad angular\( \omega\). Supondremos que la cuerda permanece en este\(xy-\) plano y\(y\) medirá su deflexión desde la posición de equilibrio,\( y=0\), sobre el\(x\) eje. De ahí que encontraremos una gráfica dando la forma de la cadena. Idealizaremos la cadena para que no tenga volumen para solo ser una curva matemática. Si tomamos un segmento pequeño y miramos la tensión en los puntos finales, vemos que esta fuerza es tangencial y asumiremos que la magnitud es la misma en ambos puntos finales. De ahí que la magnitud sea constante en todas partes y llamaremos su magnitud\(T\). Si asumimos que la desviación es pequeña, entonces podemos usar la segunda ley de Newton para obtener una ecuación

\[ Ty''+ \rho \omega^2y=0. \nonumber \]

Let\(L\) be la longitud de la cadena y la cadena se fija en los puntos inicial y final. De ahí,\( y(0)=0\) y\(y(L)=0\). Ver Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Cuerda giratoria.

Reescribimos la ecuación como\( y''+ \frac{\rho \omega^2}{T}y=0\). La configuración es similar a Ejemplo\(\PageIndex{3}\), a excepción de que la longitud del intervalo es\( L\) en lugar de\( \pi\). Estamos buscando valores propios de\( y''+ \lambda y=0, y(0)=0, y(L)=0\) dónde\( \lambda =\frac{\rho \omega^2}{T} \). Como antes no hay valores propios no positivos. Con\(\lambda>0\), la solución general a la ecuación es\(y=A \cos(\sqrt{\lambda}x)+B \sin(\sqrt{\lambda}x)\). La condición\( y(0)=0\) implica que\(A=0\) como antes. La condición\(y(L)=0\) implica eso\( \sin(\sqrt{\lambda}L)=0\) y por lo tanto\( \sqrt{\lambda}L=k \pi\) para algún número entero\( k>0\), entonces

\[ \frac{\rho \omega^2}{T}= \lambda=\frac{k^2 \pi^2}{L^2}. \nonumber \]

¿Qué dice esto sobre la forma de la cuerda? Dice que para todos los parámetros\(\rho\),\(\omega\), al\(T\) no satisfacer la ecuación anterior, la cadena está en la posición de equilibrio,\(y=0\). Cuando\(\frac{\rho \omega^2}{T} = \frac{k^2 \pi^2}{L^2}\), entonces la cuerda va a cierta distancia\(B\). No podemos calcular\(B\) con la información que tenemos.

Supongamos eso\(\rho\) y\(T\) estamos fijos y estamos cambiando\(\omega\). Para la mayoría de los valores de\(\omega\) la cadena está en el estado de equilibrio. Cuando la velocidad angular\(\omega\) alcanza un valor\(\omega = \frac{k \pi \sqrt{T}}{L\sqrt{\rho}}\), entonces la cuerda sale y tiene la forma de una onda sin que cruza los\(k-1\) tiempos del\(x\) eje -axis entre los puntos finales. Por ejemplo, at\(k=1\), la cuerda no cruza el\(x\) eje -y la forma se ve como en la Figura\(\PageIndex{1}\). Por otro lado, cuando\(k=3\) la cuerda cruza el\(x\) eje -eje 2 veces, ver Figura\(\PageIndex{2}\). Cuando vuelve a\(\omega\) cambiar, la cadena vuelve a la posición de equilibrio. Cuanto mayor sea la velocidad angular, más veces cruza el\(x\) eje -cuando se saca.

Figura\(\PageIndex{2}\): Cuerda giratoria en el tercer valor propio\((k=3)\).

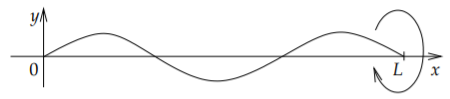
Para otro ejemplo, si tienes una cuerda de saltar giratoria (entonces\(k=1\) como está completamente) y tiras de los extremos para aumentar la tensión, entonces la velocidad también aumenta para que la cuerda se quede “reventada”.

Notas al pie

[1] Ver Ejemplo 2.2.1 y Ejemplo 2.2.3.

[2] Recordemos que\(\cosh s=\frac{1}{2}\left(e^{s}+e^{-s}\right)\) y\(\sinh s=\frac{1}{2}\left(e^{s}-e^{-s}\right)\). Como ejercicio intenta el cómputo con la solución general escrita como\(x=Ae^{\sqrt{-\lambda}t}+Be^{-\sqrt{-\lambda}t}\) (para diferentes\(A\) y por\(B\) supuesto).

[3] Nombrado así por el matemático sueco Erik Ivar Fredholm (1866—1927).