4.2: La serie trigonométrica

Funciones periódicas y motivación

Como motivación para estudiar series de Fourier, supongamos que tenemos el problema

\[\label{eq:1} x'' + \omega^2_0 x=f(t), \]

para alguna función periódica\( f(t)\). Ya lo hemos resuelto

\[\label{eq:2} x''+ \omega^2_0 x=F_0 \cos( \omega t). \]

Una forma de resolver\(\eqref{eq:1}\) es descomponerse\(f(t)\) como una suma de cosenos (y senos) y luego resolver muchos problemas de la forma\(\eqref{eq:2}\). Luego usamos el principio de superposición, para resumir todas las soluciones a las que llegamos para obtener una solución\(\eqref{eq:1}\).

Antes de continuar, hablemos un poco más en detalle sobre las funciones periódicas. Se dice que una función es periódica con periodo\(P\) si\( f(t)\) para todos\(t\). Por brevedad diremos que\( f(t)\) es\(P-\) periódico. Obsérvese que una función\(P-\)\(2P-\) periódica también es\(3P-\) periódica, periódica y así sucesivamente. Por ejemplo,\( \cos(t)\) y\( \sin(t)\) son\( 2 \pi -\) periódicos. Así son\( \cos(kt)\) y\( \sin(kt)\) para todos los enteros\( k\). Las funciones constantes son un ejemplo extremo. Son periódicos por cualquier periodo (ejercicio).

Normalmente comenzaremos con una función\(f(t)\) definida en algún intervalo\( [-L, L]\) y vamos a querer extender\(f(t)\) periodically para que sea una función\( 2L-\) periódica. Hacemos esta extensión definiendo una nueva función\(F(t)\) tal que para\(t\) en\( [-L, L]\),\( F(t)=f(t)\). Para\(t\) en\( [L, 3L]\), definimos\( F(t)=f(t-2L)\), para\(t\) en\( [-3L, -L]\)\( F(t)=f(t+2L)\), y así sucesivamente. Eso lo asumimos\( f(-L)=f(L)\). También podríamos haber comenzado con\(f\) definido solo en el intervalo medio abierto\( (-L, L]\) y luego definir\( f(-L)=f(L)\).

Ejemplo\(\PageIndex{1}\)

Definir\( f(t)=1-t^2\) en\([-1, 1]\). Ahora extender\(f(t)\) periódicamente a una función\(2\) -periódica. Ver Figura\(\PageIndex{1}\) en la página de enfrente.

Figura\(\PageIndex{1}\): Extensión periódica de la función\(1-t^{2}\).

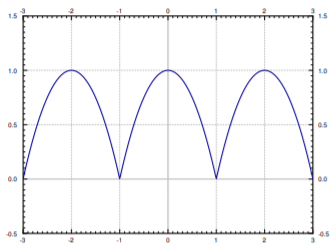
Se debe tener cuidado de distinguir entre\( f(t)\) y su extensión. Un error común es asumir que una fórmula para\( f(t)\) sostiene para su extensión. Puede resultar confuso cuando la fórmula para\( f(t)\) es periódica, pero quizás con un periodo diferente.

Ejercicio\(\PageIndex{1}\)

Definir\( f(t)= \cos t\) en\([\dfrac{ - \pi}{2}, \dfrac{ \pi}{2} ]\). Toma la extensión\(\pi -\) periódica y dibuja su gráfica. ¿Cómo se compara con la gráfica de\( \cos t\)?

Producto interno y descomposición de vectores propios

Supongamos que tenemos una matriz simétrica, es decir\( A^T=A\). Hemos dicho antes que los vectores propios de\( A\) son entonces ortogonales. Aquí la palabra ortogonal significa que si\( \vec{v}\) y\( \vec{w}\) son dos vectores propios distintos (y no múltiplos entre sí) de\( A\), entonces\( \left \langle \vec{v}, \vec{w} \right \rangle=0\). En este caso el producto interno\(\left \langle \vec{v}, \vec{w} \right \rangle\) es el producto punto, que se puede computar como\( \vec{v}^T \vec{w}\).

Para descomponer un vector\( \vec{v}\) en términos de vectores mutuamente ortogonales\( \vec{w}_1\) y\( \vec{w}_2\) escribimos

\[ \vec{v} = a_1 \vec{w}_1+a_2 \vec{w}_2. \nonumber \]

Encontremos la fórmula para\(a_1\) y\(a_2\). Primero vamos a computar

\[\langle \vec{v} , \vec{w_1} \rangle = \langle a_1 \vec{w}_1 + a_2 \vec{w}_2 , \vec{w_1} \rangle = a_1 \langle \vec{w}_1 , \vec{w_1} \rangle + a_2 \underbrace{\langle \vec{w}_2 , \vec{w_1} \rangle}_{=0} = a_1 \langle \vec{w}_1 , \vec{w_1} \rangle . \nonumber \]

Por lo tanto,

\[ a_1= \dfrac{\left \langle \vec{v}, \vec{w}_1 \right \rangle}{\left \langle \vec{w}_1, \vec{w}_1 \right \rangle}. \nonumber \]

Del mismo modo

\[ a_2= \dfrac{\left \langle \vec{v}, \vec{w}_2 \right \rangle}{\left \langle \vec{w}_2, \vec{w}_2 \right \rangle}. \nonumber \]

Probablemente recuerdes esta fórmula del cálculo vectorial.

Ejemplo\(\PageIndex{2}\)

Escribir\( \vec{v}=\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \) como una combinación lineal de\( \vec{w}_1=\left[ \begin{array}{c} 1 \\ -1 \end{array} \right] \) y\( \vec{w}_2=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \).

Primero tenga en cuenta que\( \vec{w}_1\) y\( \vec{w}_2\) son ortogonales como\( \left \langle \vec{w}_1, \vec{w}_2 \right \rangle = 1(1)+(-1)1=0\). Entonces

\[\begin{align}\begin{aligned} a_1&= \dfrac{\left \langle \vec{v}, \vec{w}_1 \right \rangle}{\left \langle \vec{w}_1, \vec{w}_1 \right \rangle}= \dfrac{2(1)+3(-1)}{1(1)+(-1)(-1)}=\dfrac{-1}{2}, \\ a_2&= \dfrac{\left \langle \vec{v}, \vec{w}_2 \right \rangle}{\left \langle \vec{w}_2, \vec{w}_2 \right \rangle}=\dfrac{2+3}{1+1}= \dfrac{5}{2}.\end{aligned}\end{align} \nonumber \]

De ahí

\[ \left[ \begin{array}{c} 2 \\ 3 \end{array} \right]=\dfrac{-1}{2} \left[ \begin{array}{c} 1 \\ -1 \end{array} \right]+ \dfrac{5}{2} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right]. \nonumber \]

Serie Trigonométrica

En lugar de descomponer un vector en términos de vectores propios de una matriz, descompondremos una función en términos de funciones propias de un cierto problema de autovalor. El problema del valor propio que usaremos para la serie de Fourier es

\[ x'' + \lambda x=0,~~~~ x(- \pi)=x(\pi)~~~~x'(- \pi)=x'( \pi). \nonumber \]

Anteriormente hemos calculado que las funciones propias son\(1, \cos(kt), \sin(kt)\). Es decir, vamos a querer encontrar una representación de una función\( 2 \pi -\) periódica\( f(t)\) como

\[ f(t)= \dfrac{a_0}{2}+ \sum^{\infty}_{n=1}a_n \cos(nt)+b_n \sin(nt). \nonumber \]

Esta serie se llama la serie de Fourier \(^{1}\)o la serie trigonométrica para\(f(t)\). Escribimos el coeficiente de la función propia\(1\) como\( \dfrac{a_0}{2}\) por conveniencia. También podríamos pensar en\( 1= \cos(0t)\), para que sólo tengamos que mirar\( \cos(kt)\) y\( \sin(kt)\).

En cuanto a las matrices queremos encontrar una proyección\(f(t)\) sobre el subespacio generada por las funciones propias. Entonces vamos a querer definir un producto interno de funciones. Por ejemplo, para encontrar\( a_n\) queremos calcular\( \left \langle f(t), \cos(nt) \right \rangle \). Definimos el producto interno como

\[ \left \langle f(t), g(t) \right \rangle = \int^{\pi}_{-\pi} f(t)g(t)dt. \nonumber \]

Con esta definición del producto interno, hemos visto en la sección anterior que las funciones propias\( \cos(kt)\) (incluyendo la función propia constante), y\( \sin(kt)\) son ortogonales en el sentido de que

\[\begin{align}\begin{aligned} \langle \, \cos (mt)\, , \, \cos (nt) \, \rangle = 0 & \qquad \text{for } m \not= n , \\ \langle \, \sin (mt)\, , \, \sin (nt) \, \rangle = 0 & \qquad \text{for } m \not= n , \\ \langle \, \sin (mt)\, , \, \cos (nt) \, \rangle = 0 & \qquad \text{for all } m \text{ and } n .\end{aligned}\end{align} \nonumber \]

Por cálculo elemental para\( n=1,2,3, \ldots .\) we have \( \left \langle \cos(nt), \cos(nt) \right \rangle = \pi\) y\( \left \langle \sin(nt), \sin(nt) \right \rangle = \pi\). Por la constante que obtenemos

\[ \left \langle 1, 1 \right \rangle = \int_{\pi}^{\pi}1\cdot 1\: dt= 2 \pi. \nonumber \]

Los coeficientes vienen dados por

\[\begin{align}\begin{aligned} a_n &= \dfrac{ \left \langle f(t), \cos(nt) \right \rangle}{\left \langle \cos(nt), \cos(nt) \right \rangle}= \dfrac{1}{ \pi} \int^{\pi}_{-\pi} f(t) \cos(nt)dt, \\ b_n &= \dfrac{ \left \langle f(t), \sin(nt) \right \rangle}{\left \langle \sin(nt), \sin(nt) \right \rangle}= \dfrac{1}{ \pi} \int^{\pi}_{-\pi} f(t) \sin(nt)dt.\end{aligned}\end{align} \nonumber \]

Compara estas expresiones con el ejemplo finito-dimensional. Porque\( a_0\) obtenemos una fórmula similar

\[ a_0 = 2 \dfrac{ \left \langle f(t), 1 \right \rangle}{\left \langle 1, 1 \right \rangle} \dfrac{1}{ \pi} \int^{\pi}_{-\pi} f(t)dt. \nonumber \]

Comprobemos las fórmulas usando las propiedades de ortogonalidad. Supongamos por un momento que

\[ f(t)= \frac{a_0}{2}+ \sum^\infty_{n=1}a_n \cos(nt)+b_n \sin(nt). \nonumber \]

Entonces para\( m \geq 1\) nosotros tenemos

\[\begin{align}\begin{aligned} \left \langle f(t), \cos(mt) \right \rangle &= \left \langle \frac{a_0}{2}+ \sum^\infty_{n=1}a_n \cos(nt)+b_n \sin(nt), \cos(mt) \right \rangle \\ &=\frac{a_0}{2}\left \langle 1, \cos(mt) \right \rangle +\sum^\infty_{n=1}a_n \left \langle \cos(nt), \cos(mt) \right \rangle + b_n \left \langle \sin(nt), \sin(mt) \right \rangle \\ &= a_m \left \langle \cos(mt), \cos(mt) \right \rangle . \end{aligned}\end{align} \nonumber \]

Y por lo tanto\( a_m=\frac{\left \langle f(t), \cos(mt) \right \rangle}{\left \langle \cos(mt), \cos(mt) \right \rangle}.\)

Ejercicio\(\PageIndex{2}\)

Realizar el cálculo para\(a_0\) y\(b_m\).

Ejemplo\(\PageIndex{3}\)

Toma la función

\[ f(t)=t \nonumber \]

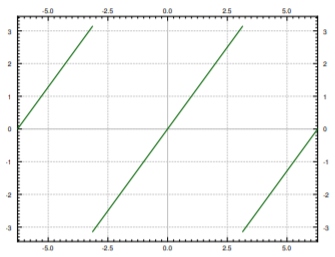
para\(t\) en\((- \pi, \pi]\). Extender\( f(t)\) periódicamente y escribirlo como una serie de Fourier. Esta función se llama diente de sierra.

La gráfica de la función periódica extendida se da en la Figura\(\PageIndex{2}\). Calculemos los coeficientes.

Figura\(\PageIndex{2}\): La gráfica de la función de diente de sierra.

Solución

Empezamos con\(a_0\),

\[ a_0 = \frac{1}{\pi} \int^\pi_{-\pi} tdt=0. \nonumber \]

A menudo usaremos el resultado del cálculo que dice que la integral de una función impar sobre un intervalo simétrico es cero. Recordemos que una función impar es una función\( \varphi(t)\) tal que\( \varphi(-t) = - \varphi(t)\). Por ejemplo las funciones\( t, \sin t\), o (lo que es importante para nosotros)\( t \cos(nt)\) son todas funciones impares. Por lo tanto

\[ a_n=\frac{1}{\pi} \int^\pi_{-\pi} t \cos(nt)dt=0. \nonumber \]

Pasemos a\( b_n\). Otro dato útil del cálculo es que la integral de una función par sobre un intervalo simétrico es el doble de la integral de la misma función en la mitad del intervalo. Recordar una función par es una función\(\varphi(t)\) tal que\( \varphi(-t) = \varphi(t)\). Por ejemplo\( t \sin(nt)\) es parejo.

\[\begin{align}\begin{aligned} b_n &= \frac{1}{\pi} \int^\pi_{-\pi} t \sin(nt)dt \\ &= \frac{2}{\pi} \int^\pi_{0} t \sin(nt)dt \\ &= \frac{2}{\pi} \left( \left[ \frac{-t \cos(nt)}{n}\right] ^\pi_{t=0}+\frac{1}{n} \int^\pi_{0} \cos(nt)dt\right) \\ &= \frac{2}{\pi} \left( \frac{- \pi \cos(n \pi)}{n}+0\right) \\ &= \frac{-2 \cos(n \pi)}{n}=\frac{2(-1)^{n+1}}{n}.\end{aligned}\end{align} \nonumber \]

Hemos utilizado el hecho de que

\[ \cos(n \pi)=(-1)^n= \left\{ \begin{array}{c} 1~~~~ {\rm{~if~}} n {\rm{~even,~}}\\ -1~~~~ {\rm{~if~}} n {\rm{~odd.~}} \end{array} \right. \nonumber \]

La serie, por lo tanto, es

\[ \sum^\infty_{n=1} \frac{2(-1)^{n+1}}{n} \sin(nt). \nonumber \]

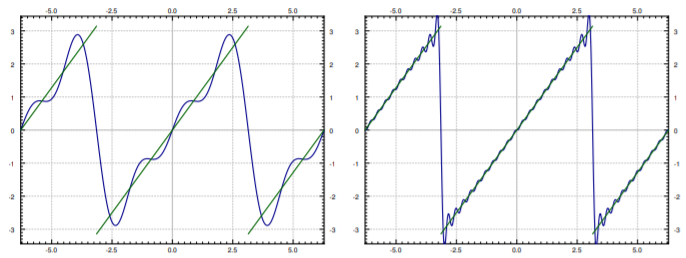
Escribamos los primeros\(3\) armónicos de la serie para\(f(t)\).

\[ 2 \sin(t)- \sin(2t)+ \frac{2}{3} \sin(3t)+ \cdots \nonumber \]

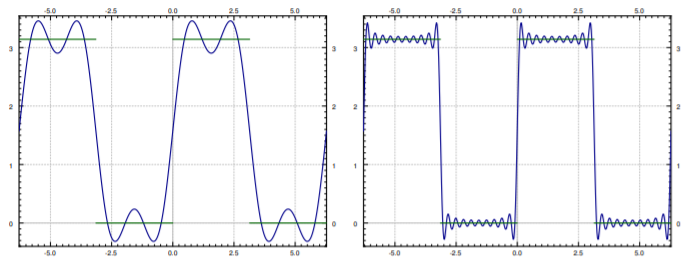
La trama de estos tres primeros términos de la serie, junto con una gráfica de los primeros\(20\) términos se da en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Primeros 3 (gráfica izquierda) y 20 (gráfica derecha) armónicos de la función diente de sierra.

Ejemplo\(\PageIndex{4}\)

Toma la función

\[ f(t)= \left\{ \begin{array}{cc} 0&~~~~ {\rm{~if~}} - \pi < t \leq 0, \\ \pi& {\rm{~if~}} 0 < t \leq \pi. \end{array} \right. \nonumber \]

Extender\(f(t)\) periódicamente y escribirlo como una serie de Fourier. Esta función o sus variantes aparecen a menudo en aplicaciones y la función se llama onda cuadrada.

Figura\(\PageIndex{4}\): La gráfica de la función de onda cuadrada.

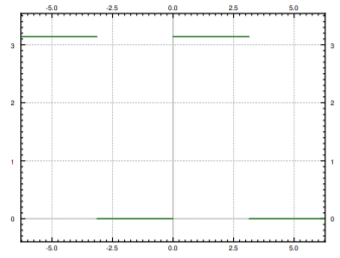
La gráfica de la función periódica extendida se da en la Figura\(\PageIndex{4}\). Ahora calculamos los coeficientes. Empecemos con\(a_0\)

\[ a_0= \frac{1}{\pi} \int^\pi_{-\pi} f(t)dt= \frac{1}{\pi} \int^\pi_{0} \pi dt= \pi . \nonumber \]

Siguiente,

\[ a_n = \frac{1}{\pi} \int^\pi_{-\pi} f(t) \cos(nt)dt= \frac{1}{\pi} \int^\pi_{0} \pi \cos(nt)dt= 0 . \nonumber \]

Y finalmente

\[\begin{align}\begin{aligned} b_n &= \frac{1}{\pi} \int^\pi_{-\pi} f(t) \sin(nt)dt \\ &= \frac{1}{\pi} \int^\pi_{0} \pi \sin(nt)dt \\ &= \left[ \frac{- \cos(nt)}{n}\right]_{t=0}^{\pi} \\ &=\frac{1- \cos( \pi n)}{n}=\frac{1-(-1)^n}{n}= \left\{ \begin{array}{c} \frac{2}{n}~~~~ {\rm{~if~}} n {\rm{~is~odd,~}}\\ 0~~~~ {\rm{~if~}} n {\rm{~is~even.~}} \end{array} \right. \end{aligned}\end{align} \nonumber \]

La serie de Fourier es

\[ \frac{\pi}{2} + \sum^{\infty}_{n=1~ n~ \rm{odd}} \frac{2}{n} \sin(nt)+\sum^{\infty}_{k=1} \frac{2}{2k-1} \sin((2k-1)t). \nonumber \]

Escribamos los primeros 3 armónicos de la serie para\(f(t)\).

\[ \frac{\pi}{2}+2 \sin(t)+ \frac{2}{3} \sin(3t)+ \cdots \nonumber \]

La gráfica de estos tres primeros y también de los primeros 20 términos de la serie se da en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Primeros 3 (gráfica izquierda) y 20 (gráfica derecha) armónicos de la función de onda cuadrada.

Hasta el momento hemos rodado el tema de la convergencia. Por ejemplo, si\(f(t)\) es la función de onda cuadrada, la ecuación

\[ f(t)= \frac{\pi}{2} + \sum_{k=1}^{\infty}\frac{2}{2k-1} \sin((2k-1)t). \nonumber \]

es sólo una igualdad para tal\(t\) donde\(f(t)\) es continuo. Es decir, no obtenemos una igualdad para\(t= - \pi, 0, \pi\) y todas las demás discontinuidades de\(f(t)\). No es difícil ver que cuando\(t\) es un múltiplo entero de\(\pi\) (que incluye todas las discontinuidades), entonces

\[ \frac{\pi}{2} + \sum_{k=1}^{\infty}\frac{2}{2k-1} \sin((2k-1)t)=\frac{\pi}{2}. \nonumber \]

Redefinimos\(f(t)\)\([- \pi, \pi]\) como

\[ f(t)=\left\{ \begin{array}{cc} 0 &~~~~ {\rm{~if~}} - \pi<t<0, \\ \pi & {\rm{~if~}} 0<t<\pi, \\ \pi/2& ~~~~~~~~~~~~~~~~~~ {\rm{~if~}} t= - \pi, t=0, {\rm{~or~}} t=\pi, \end{array} \right. \nonumber \]

y extender periódicamente. La serie equivale a esta extendida\(f(t)\) en todas partes, incluyendo las discontinuidades. Generalmente no nos preocuparemos por cambiar los valores de la función en varios puntos (finitamente muchos).

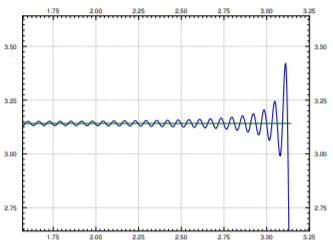
Diremos más sobre la convergencia en la siguiente sección. Sin embargo, mencionemos brevemente un efecto de la discontinuidad. Amplémonos cerca de la discontinuidad en la onda cuadrada. Además, trazemos los primeros 100 armónicos, ver Figura\(\PageIndex{6}\). Notarás que si bien la serie es una muy buena aproximación lejos de las discontinuidades, el error (el sobreimpulso) cerca de la discontinuidad en\( t= \pi\) no parece ser cada vez más pequeño. Este comportamiento se conoce como el fenómeno Gibbs. La región donde el error es grande sí se hace más pequeña, sin embargo, cuantos más términos tomemos en la serie.

Figura\(\PageIndex{6}\): Fenómeno de Gibbs en acción.

Podemos pensar en una función periódica como una “señal” siendo una superposición de muchas señales de pura frecuencia. Por ejemplo, podríamos pensar en la onda cuadrada como un tono de cierta frecuencia base. Esta frecuencia base se llama la frecuencia fundamental. La onda cuadrada será una superposición de muchos tonos puros diferentes de frecuencias que son múltiplos de la frecuencia fundamental. En la música, las frecuencias más altas se llaman los armónicos. Todas las frecuencias que aparecen se llaman el espectro de la señal. Por otro lado una onda sinusoidal simple es sólo el tono puro (sin armónicos). La forma más sencilla de hacer sonido usando una computadora es la onda cuadrada, y el sonido es muy diferente de un tono puro. Si alguna vez jugaste videojuegos de la década de 1980 más o menos, entonces escuchaste cómo suenan las ondas cuadradas.

Notas al pie

[1] Nombrado así por el matemático francés Jean Baptiste Joseph Fourier (1768 — 1830).