4.3: Más información sobre la serie de Fourier
- Page ID
- 115367
Antes de leer la conferencia, puede ser bueno probar primero el Proyecto IV (serie de Fourier) desde el sitio web del IODE: https://conf.math.illinois.edu/iode/fsgui.html. Después de leer la conferencia puede ser bueno continuar con el Proyecto V (serie de Fourier nuevamente).
2L-Funciones Periódicas
Hemos calculado la serie de Fourier para una función\(2 \pi\) -periódica, pero ¿qué pasa con las funciones de diferentes períodos? Bueno, no temas, el cómputo es un simple caso de cambio de variables. Solo podemos reescalar el eje independiente. Supongamos que tenemos una función\(2L\) -periódica\(f(t)\) (\(L\)se llama el medio periodo). Vamos\( S= \dfrac{\pi}{L}t\). Luego la función
\[ g(s)=f \left( \dfrac{L}{\pi}s \right) \nonumber \]
es\(2 \pi\) -periódico. También queremos reescalar todos nuestros senos y cosenos. Queremos escribir
\[ f(t)= \dfrac{a_0}{2}+ \sum_{n=1}^{\infty}a_n \cos \left( \dfrac{n \pi}{L}t \right) + b_n \sin \left( \dfrac{n \pi}{L}t \right). \nonumber \]
Si cambiamos las variables a\( s\) vemos que
\[ g(s)= \dfrac{a_0}{2}+ \sum_{n=1}^{\infty}a_n \cos(ns) + b_n \sin(ns). \nonumber \]
Calculamos\( a_n\) y\( b_n\) como antes. Después de anotar las integrales cambiamos las variables de\( s\) back to\( t\).
\[\begin{aligned} a_0 &= \dfrac{1}{\pi} \int_{-\pi}^{\pi}g(s)ds=\dfrac{1}{L} \int_{-L}^{L}f(t)dt, \\ a_n &= \dfrac{1}{\pi} \int_{-\pi}^{\pi}g(s) \cos(ns)ds=\dfrac{1}{L} \int_{-L}^{L}f(t) \cos \left( \dfrac{n \pi}{L}t \right)dt, \\ b_n &= \dfrac{1}{\pi} \int_{-\pi}^{\pi}g(s) \sin(ns)ds=\dfrac{1}{L} \int_{-L}^{L}f(t) \sin \left( \dfrac{n \pi}{L}t \right)dt. \end{aligned} \nonumber \]
Los dos medios periodos más comunes que aparecen en los ejemplos son\(\pi\) y\(1\) por la sencillez. Debemos recalcar que no hemos hecho nuevas matemáticas, solo hemos cambiado variables. Si entiende la serie de Fourier para funciones\(2 \pi\) -periódicas, la entiende para funciones\(2L\) -periódicas. Todo lo que estamos haciendo es mover algunas constantes alrededor, pero todas las matemáticas son iguales.
Let
\[ f(t)=|t|~~~~~ {\rm{~for~}} -1<t \leq 1, \nonumber \]
extendido periódicamente. La gráfica de la extensión periódica se da en la Figura\(\PageIndex{1}\). Calcular la serie de Fourier de\( f(t)\).
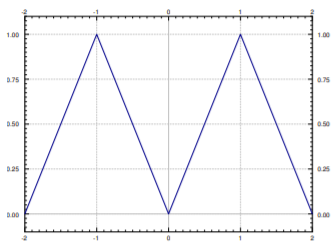
Solución
Queremos escribir\(f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos (n\pi t)+b_{n}\sin (n\pi t)\). Para\(n\geq 1\) notamos que\(|t|\cos (n\pi t)\) es parejo y por lo tanto
\[\begin{align}\begin{aligned} a_n &= \int_{-1}^{1} f(t) \cos( n \pi t)dt \\ &= 2 \int_{0}^{1} t \cos( n \pi t)dt \\ &= 2 \left[ \dfrac{t}{n \pi} \sin(n \pi t)\right] _{t=0}^{1} - 2 \int_{0}^{1} \dfrac{1}{n \pi} \sin(n \pi t)dt \\ &=0 + \dfrac{1}{n^2 \pi^2} \left[ \cos(n \pi t)\right] _{t=0}^{1} = \dfrac{2((-1)^n-1)}{n^2 \pi^2}= \left\{ \begin{array}{cc} 0 & {\rm{~if~}} {\it{n}} {\rm{~is~even,}}\\ \dfrac{-4}{n^2 \pi^2} & {\rm{~if~}} {\it{n}} {\rm{~is~odd.}} \end{array} \right. \end{aligned}\end{align} \nonumber \]
A continuación encontramos\(a_0\)
\[ a_0 = \int_{-1}^{1} |t|dt=1. \nonumber \]
Deberías poder encontrar esta integral pensando en la integral como el área debajo de la gráfica sin hacer ningún cálculo en absoluto. Por último podemos encontrar\( b_n\). Aquí, notamos que\(|t| \sin(n \pi t)\) es extraño y, por lo tanto,
\[ b_n= \int_{-1}^{1} f(t) \sin( n \pi t)dt=0. \nonumber \]
Por lo tanto, la serie es
\[ \dfrac{1}{2}+ \sum_{\underset{n~ \rm{odd}}{n=1}}^{\infty} \dfrac{-4}{n^2 \pi^2} \cos(n \pi t) \nonumber \]
Anote explícitamente los primeros términos de la serie hasta la\( 3^{\rm{rd}}\) armónica.
\[ \dfrac{1}{2}- \dfrac{4}{\pi^2} \cos(\pi t)- \dfrac{4}{9 \pi^2} \cos(3 \pi t)- \cdots \nonumber \]
La trama de estos pocos términos y también una gráfica hasta la\( 20^{\rm{th}}\) armónica se da en la Figura\(\PageIndex{2}\). Deberías notar lo cerca que está la gráfica a la función real. También debes notar que no hay “fenómeno Gibbs” presente ya que no hay discontinuidades.
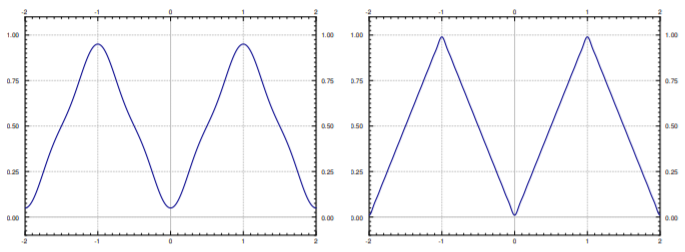
Convergencia
Necesitaremos los límites unilaterales de las funciones. Usaremos la siguiente notación
\[f(c-) = \lim_{t \uparrow c} f(t), \qquad \text{and} \qquad f(c+) = \lim_{t \downarrow c} f(t). \nonumber \]
Si no está familiarizado con esta notación,\( \lim_{t \uparrow c} f(t) \) significa que estamos tomando un límite de\( f(t)\) como\(t\) enfoques\(c\) desde abajo (es decir\( t<c\)) y\(\lim_{t \downarrow c} f(t)\) significa que estamos tomando un límite de\( f(t)\) como\(t\) enfoques\(c\) desde arriba (es decir\( t>c\)). Por ejemplo, para la función de onda cuadrada
\[\label{eq:12} f(t)= \left\{ \begin{array}{ccc} 0 & \rm{if}& - \pi < t \leq 0, \\ \pi & \rm{if} & 0 < t \leq \pi , \end{array} \right. \]
tenemos\( f(0-)=0\) y\( f(0+)= \pi\).
Let\( f(t)\) Ser una función definida en un intervalo\([a,b]\). Supongamos que encontramos finitamente muchos puntos\( a=t_0, t_1, t_2, \ldots , t_k=b\) en el intervalo, tal que\( f(t)\) es continuo en los intervalos\( (t_0,t_1), (t_1,t_2), \ldots , (t_{k-1},t_k)\). También supongamos que todos los límites unilaterales existen, es decir, todos\( f(t_0+), f(t_1-), f(t_1+), f(t_2-), f(t_2+), \ldots , f(t_k-)\) existen y son finitos. Entonces decimos que\( f(t)\) es continuo por partes.
Si además,\( f(t)\) es diferenciable en todos pero finitamente muchos puntos, y\( f'(t)\) es continuo por tramos, entonces\( f(t)\) se dice que es liso por partes.
La función de onda cuadrada\(\eqref{eq:12}\) es lisa en\( [- \pi, \pi]\) o en cualquier otro intervalo. En tal caso simplemente decimos que la función es por partes lisa.
La función\(f(t)=|t|\) es lisa por partes.
La función no\(f(t)= \dfrac{1}{t}\) es uniforme por partes\( [-1, 1]\) (o cualquier otro intervalo que contenga cero). De hecho, ni siquiera es continuo por partes.
La función no\(f(t)=\sqrt[3]{t}\) es uniforme por partes\( [- 1, 1]\) (o cualquier otro intervalo que contenga cero). \( f(t)\)es continua, pero la derivada de no\( f(t)\) está limitada cerca de cero y, por lo tanto, no continua por tramos.
Las funciones suaves por partes tienen una respuesta fácil sobre la convergencia de la serie de Fourier.
Supongamos que\( f(t)\) es una función suave\(2L\) -periódica por partes. Let
\[ \dfrac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \dfrac{n \pi}{L}t \right)+b_n \sin \left( \dfrac{n \pi}{L}t \right) \nonumber \]
ser la serie de Fourier para\( f(t)\). Entonces la serie converge para todos\(t\). Si\( f(t)\) es continuo cerca\(t\), entonces
\[ f(t)= \dfrac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \dfrac{n \pi}{L}t \right)+b_n \sin \left( \dfrac{n \pi}{L}t \right). \nonumber \]
De lo contrario
\[ \dfrac{f(t-)+f(t+)}{2}= \dfrac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \dfrac{n \pi}{L}t \right)+b_n \sin \left( \dfrac{n \pi}{L}t \right). \nonumber \]
Si sucede que tenemos eso\( f(t)= \dfrac{f(t-)+f(t+)}{2}\) en todas las discontinuidades, la serie de Fourier converge a\( f(t)\) todas partes. Siempre podemos redefinir\( f(t)\) cambiando el valor en cada discontinuidad apropiadamente. Entonces podemos escribir un signo de igual entre\( f(t)\) y la serie sin ninguna preocupación. Mencionamos brevemente este hecho al final del último apartado.
Tenga en cuenta que el teorema no dice qué tan rápido converge la serie. Piense en la discusión del fenómeno Gibbs en la última sección. Cuanto más se acerque a la discontinuidad, más términos necesitará tomar para obtener una aproximación precisa a la función.
Diferenciación e Integración de las Series de Fourier
Las series de Fourier no solo convergen muy bien, sino que es fácil de diferenciar e integrar la serie. Podemos hacer esto simplemente diferenciando o integrando término por término.
Supongamos
\[ f(t)= \dfrac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \dfrac{n \pi}{L}t \right)+b_n \sin \left( \dfrac{n \pi}{L}t \right) \nonumber \]
es una función continua lisa por partes y la derivada\( f'(t)\) es lisa por partes. Entonces la derivada se puede obtener diferenciando término por término,
\[ f'(t)= \sum^{\infty}_{n=1} \dfrac{-a_n n \pi}{L} \sin \left( \dfrac{n \pi}{L}t \right)+\dfrac{b_n n \pi}{L} \cos \left( \dfrac{n \pi}{L}t \right). \nonumber \]
Es importante que la función sea continua. Puede tener esquinas, pero no saltos. De lo contrario las series diferenciadas no lograrán converger. Para un ejercicio, toma la serie obtenida para la onda cuadrada e intenta diferenciar la serie. Del mismo modo, también podemos integrar una serie de Fourier.
Supongamos
\[ f(t)= \dfrac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \dfrac{n \pi}{L}t \right)+b_n \sin \left( \dfrac{n \pi}{L}t \right) \nonumber \]
es una función suave por tramos. Entonces se obtiene el antiderivado por antidiferenciación término por término y así
\[ F(t)= \dfrac{a_0 t}{2}+ C+ \sum^{\infty}_{n=1} \dfrac{a_n L}{n \pi} \sin \left( \dfrac{n \pi}{L}t \right)+\dfrac{-b_n L}{n \pi} \cos \left( \dfrac{n \pi}{L}t \right), \nonumber \]
donde\(F'(t)=f(t)\) y\(C\) es una constante arbitraria.
Tenga en cuenta que la serie para ya no\( F(t)\) es una serie de Fourier ya que contiene el\( \dfrac{a_0 t}{2}\) término. La antiderivada de una función periódica ya no necesita ser periódica y por lo tanto no debemos esperar una serie de Fourier.
Tasas de Convergencia y Suavidad
Hagamos un ejemplo de una función periódica con una derivada en todas partes.
Toma la función
\[ f(t)= \left\{ \begin{array}{ccc} (t+1)t & \rm{if}& -1 < t \leq 0, \\ (1-t)t & \rm{if} & 0 < t \leq 1 , \end{array} \right. \nonumber \]
y extender a una función 2-periódica. La gráfica se da en la Figura\(\PageIndex{3}\).
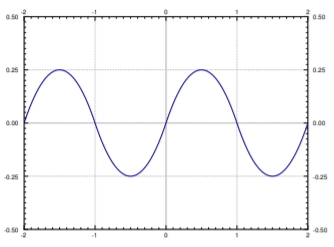
Tenga en cuenta que esta función tiene una derivada en todas partes, pero no tiene una segunda derivada siempre que\(t\) sea un número entero.
Cómputos\( f''(0+)\) y\( f''(0-)\).
Calculemos los coeficientes de la serie de Fourier. El cómputo real implica varias integraciones por partes y se deja en manos del estudiante.
\[\begin{align}\begin{aligned} a_0 &= \int_{-1}^1 f(t)dt= \int_{-1}^0 (t+1)tdt+ \int_{0}^1 (1-t)tdt=0, \\ a_n &= \int_{-1}^1 f(t) \cos(n \pi t)dt= \int_{-1}^0 (t+1)t \cos(n \pi t)dt+ \int_{0}^1 (1-t)t \cos(n \pi t)dt=0 \\ b_n &= \int_{-1}^1 f(t) \sin(n \pi t)dt= \int_{-1}^0 (t+1)t \sin(n \pi t)dt+ \int_{0}^1 (1-t)t \sin(n \pi t)dt \\ &= \dfrac{4(1-(-1)^n)}{\pi^3 n^3}= \left\{ \begin{array}{cc} \dfrac{8}{\pi^3 n^3} & {\rm{~if~}} {\it{n}} {\rm{~is~odd,}}\\ 0 & {\rm{~if~}} {\it{n}} {\rm{~is~even.}} \end{array} \right.\end{aligned}\end{align} \nonumber \]
Es decir, la serie es
\[ \sum_{\underset{n~ \rm{odd}}{n=1}}^{\infty} \dfrac{8}{\pi^3 n^3} \sin(n \pi t). \nonumber \]
Esta serie converge muy rápido. Si trazas hasta el tercer armónico, esa es la función
\[ \dfrac{8}{\pi^3} \sin(\pi t)+ \dfrac{8}{27 \pi^3} \sin(3 \pi t), \nonumber \]
es casi indistinguible de la trama de\( f(t)\) en Figura\(\PageIndex{3}\). De hecho, el coeficiente ya\( \dfrac{8}{27 \pi^3} \) es apenas 0.0096 (aproximadamente). El motivo de este comportamiento es el\(n^3\) término en el denominador. Los coeficientes\( b_n\) en este caso van a cero tan rápido como\(\dfrac{1}{n^3}\) va a cero.
Para las funciones construidas por tramos a partir de polinomios como anteriormente, generalmente es cierto que si tiene una derivada, los coeficientes de Fourier irán a cero aproximadamente como\(\dfrac{1}{n^3}\). Si solo tienes una función continua, entonces los coeficientes de Fourier irán a cero como\(\dfrac{1}{n^2}\). Si tienes discontinuidades, entonces los coeficientes de Fourier irán a cero aproximadamente como\(\dfrac{1}{n}\). Para funciones más generales la historia es algo más complicada pero la misma idea sostiene, cuanto más derivadas tengas, más rápidos serán los coeficientes que van a cero. Razonamiento similar funciona a la inversa. Si los coeficientes van a cero como siempre\(\dfrac{1}{n^2}\) obtienes una función continua. Si van a cero como\(\dfrac{1}{n^3}\) tú obtienes una función diferenciable en todas partes.
Para justificar este comportamiento, tomemos por ejemplo la función definida por la serie de Fourier
\[ f(t)= \sum_{n=1}^{\infty} \dfrac{1}{n^3} \sin(nt). \nonumber \]
Cuando diferenciamos término por término notamos
\[ f'(t)= \sum_{n=1}^{\infty} \dfrac{1}{n^2} \cos(nt). \nonumber \]
Por lo tanto, los coeficientes ahora bajan como\(\dfrac{1}{n^2}\), lo que significa que tenemos una función continua. La derivada de\( f'(t)\) se define en la mayoría de los puntos, pero hay puntos donde no\( f'(t)\) es diferenciable. Tiene esquinas, pero no saltos. Si nos diferenciamos de nuevo (donde podemos) nos encontramos con que la función\( f''(t)\), ahora no puede ser continua (tiene saltos)
\[ f''(t)= \sum_{n=1}^{\infty} \dfrac{-1}{n} \sin(nt). \nonumber \]
Esta función es similar a la del diente de sierra. Si intentáramos volver a diferenciar la serie obtendríamos ¡la\[ \sum_{n=1}^{\infty} - \cos(nt), \nonumber \] cual no converge!
Utilizar una computadora para trazar la serie que obtuvimos para\( f(t)\),\( f'(t)\) y\( f''(t)\). Es decir, trama dicen los primeros\(5\) armónicos de las funciones. ¿En qué puntos\( f''(t)\) tiene las discontinuidades?


