4.4: Serie de seno y coseno

4.4.1: Incluso Funciones Periódicas

Es posible que ya hayas notado que una función impar no tiene términos coseno en la serie de Fourier y una función par no tiene términos sinusoidales en la serie de Fourier. Esta observación no es una coincidencia. Veamos con más detalle la función periódica par e impar.

Recordemos que una función\(f(t)\) es impar si\(f(-t) = -f(t)\). Una función\(f(t)\) es incluso si\(f(-t) = f(t)\). Por ejemplo,\(\cos{(nt)}\) es par y\(\sin{(nt)}\) es impar. Del mismo modo la función\(t^k\) es par si\(k\) es par e impar cuando\(k\) es impar.

Ejercicio\(\PageIndex{1}\)

Toma dos funciones\(f(t)\)\(g(t)\) y define su producto\(h(t) =f(t)\,g(t)\).

1. ¿Supongamos que ambos\(f(t)\) and \(g(t)\) are odd, is\(h(t)\) pares o pares?
2. Supongamos que uno es par y uno es impar, ¿es\(h(t)\) impar o par?
3. Supongamos que ambos son pares, ¿es\(h(t)\) impar o par?

Si\(f(t)\) y\(g(t)\) son ambos impares, entonces\(f(t) + g(t)\) es impar. De manera similar para funciones pares. Por otro lado, si\(f(t)\) es impar y\(g(t)\) par, entonces no podemos decir nada sobre la suma\(f(t) + g(t)\). De hecho, la serie de Fourier de cualquier función es una suma de una función impar (los términos sinusoidales) y par (los términos coseno).

En esta sección consideramos funciones periódicas impares e impares. Anteriormente hemos definido la extensión\(2L\) -periódica de una función definida en el intervalo\([-L,L]\). A veces solo nos interesa la función en el rango\([0,L]\) y sería conveniente tener una función impar (resp. par). Si la función es impar (resp. par), todos los términos coseno (resp. seno) desaparecerán. Lo que haremos es tomar la extensión impar (resp. par) de la función\([-L,L]\) y luego extender periódicamente a una función\(2L\) -periódica.

Toma una función\(f(t)\) definida en\([0,L]\). En\((-L,L]\) definir las funciones

\[\begin{align}\begin{aligned} F_{\rm{odd}}(t)& \overset{ \rm{def}}{=} \left\{ \begin{array}{ccc} f(t) & \rm{if} & 0 \leq t \leq L, \\ -f(-t) & \rm{if} & -L < t < 0, \end{array} \right. \\ F_{\rm{even}}(t)& \overset{ \rm{def}}{=} \left\{ \begin{array}{ccc} f(t) & \rm{if} & 0 \leq t \leq L, \\ f(-t) & \rm{if} & -L < t < 0. \end{array} \right. \end{aligned}\end{align} \nonumber \]

Extender\(F_{odd}(t)\) y\(F_{even}(t)\) ser\(2L\) -periódico. Entonces\(F_{odd}(t)\) se llama la extensión periódica impar de\(f(t)\), y\(F_{even}(t)\) se llama la extensión periódica par de\(f(t)\). Para la extensión impar generalmente asumimos que\(f(0)=f(L)=0\).

Ejercicio\(\PageIndex{2}\)

Comprueba que\(F_{odd}(t)\) sea impar y que\(F_{even}(t)\) sea par. Para\(F_{odd}\), assume \(f(0)=f(L)=0\).

Ejemplo\(\PageIndex{1}\)

Toma la función\(f(t) = t(1-t)\) definida en\([0,1]\). La figura\(\PageIndex{1}\) muestra las gráficas de las extensiones pares e impares de\(f(t)\).

Figura\(\PageIndex{1}\): Extensión\(2\) periódica impar y par de\(f(t)=t(1-t)\),\(0\leq t\leq 1\).

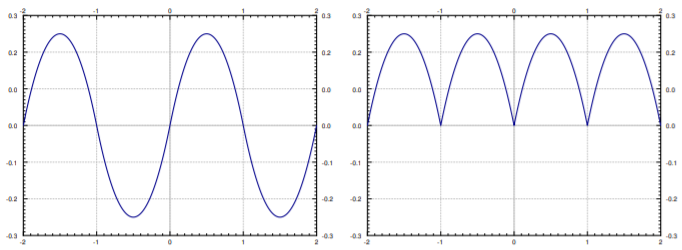
Serie de seno y coseno

Let\(f(t)\) Ser una función impar\(2L\) -periódica. Escribimos la serie de Fourier para\(f(t)\). Primero, calculamos los coeficientes\(a_n\) (incluidos\( n=0 \)) y obtenemos

\[a_n = \dfrac{1}{L} \int _{-L}^L f(t) \text{cos} \left(\frac{n\pi}{L}t \right) dt = 0. \nonumber \]

Es decir, no hay términos coseno en la serie de Fourier de una función impar. La integral es cero porque\( f(t) \cos{(\frac{n\pi}{L}t)}\) es una función impar (producto de una función impar y una función par es impar) y la integral de una función impar sobre un intervalo simétrico es siempre cero. La integral de una función par en un intervalo simétrico\([-L,L]\) es el doble de la integral de la función en el intervalo\([0,L]\). La función\(f(t) \sin{(\frac{n\pi}{L}t)}\) es producto de dos funciones impares y por lo tanto es par.

\[ b_n = \dfrac{1}{L} \int_{-L}^L f(t) \sin{\left( \dfrac{n\pi}{L}t \right)}\,dt = \dfrac{2}{L} \int_{0}^L f(t) \sin{\left( \dfrac{n\pi}{L}t \right)}\,dt. \nonumber \]

Ahora escribimos la serie de Fourier de\(f(t)\) como

\[ \sum_{n=1}^{\infty} b_n \sin{\left( \dfrac{n\pi}{L}t \right)}. \nonumber \]

Del mismo modo, si\(f(t)\) es una función par\(2L\) -periódica. Por las mismas razones exactas que anteriormente, encontramos que\(b_n=0\) y

\[a_n = \dfrac{2}{L} \int_0^{L} f(t) \cos{\left( \dfrac{n\pi}{L}t\right)} \, dt. \nonumber \]

La fórmula aún funciona para\(n=0\), en cuyo caso se convierte en

\[a_0= \dfrac{2}{L}\int_0^L f(t)\, dt. \nonumber \]

La serie de Fourier es entonces

\[ \dfrac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos{\left( \dfrac{n\pi}{L} t \right)}. \nonumber \]

Una consecuencia interesante es que los coeficientes de la serie de Fourier de una función impar (o par) se pueden calcular simplemente integrando sobre el medio intervalo\([0,L]\). Por lo tanto, podemos calcular la serie de Fourier de la extensión impar (o par) de una función calculando ciertas integrales a lo largo del intervalo donde se define la función original.

Teorema\(\PageIndex{1}\)

Dejar\(f(t)\) ser una función suave por partes definida en\([0,L]\). Entonces la extensión periódica impar de\(f(t)\) tiene la serie de Fourier

\[ F_{odd}(t) = \sum_{n=1}^{\infty} b_n \sin{\left(\dfrac{n\pi}{L}t\right)}, \nonumber \]

donde

\[ b_n = \dfrac{2}{L} \int_0^{L} f(t) \sin{\left( \dfrac{n\pi}{L} t \right)} \,dt. \nonumber \]

La extensión periódica uniforme de\(f(t)\) tiene la serie de Fourier

\[ F_{even}(t) = \dfrac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos{\left(\dfrac{n\pi}{L}t\right)}, \nonumber \]

donde

\[ a_n = \dfrac{2}{L} \int_0^{L} f(t) \cos{\left( \dfrac{n\pi}{L} t \right)} \,dt. \nonumber \]

La serie\( \sum_{n=1}^{\infty} b_n \sin{\left(\dfrac{n\pi}{L}t\right)}\) se llama la serie sinusoidal de\(f(t)\) y la serie\( \dfrac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos{\left(\dfrac{n\pi}{L}t\right)}\) se llama la serie coseno de\(f(t)\). A menudo en realidad no nos importa lo que suceda fuera de\([0,L]\). En este caso, elegimos la serie que mejor se ajuste a nuestro problema.

No es necesario comenzar con la serie completa de Fourier para obtener las series de seno y coseno. La serie sinusoidal es realmente la expansión de la función propia del\(f(t)\) uso de funciones propias del problema del valor propio\(x''+\lambda x=0\)\(x(0)=0\),\(x(L)=L\). La serie coseno es la expansión de la función propia del\(f(t)\) uso de funciones propias del problema del valor propio\(x''+\lambda x=0\),\(x'(0)=0\),\(x'(L)=L\). Podríamos haber obtenido, por lo tanto, las mismas fórmulas definiendo el produ interno

\[ \left \langle f(t),g(y)\right \rangle =\int _0^L f(t)g(t)\,dt, \nonumber \]

y siguiendo el procedimiento de la Sección 4.2. Este punto de vista es útil, ya que comúnmente usamos una serie específica que surgió porque nuestra pregunta subyacente condujo a un cierto problema de autovalor. Si el problema del valor propio no es uno de los tres que cubrimos hasta ahora, aún se puede hacer una expansión de función propia, generalizando los resultados de este capítulo. Nos ocuparemos de tal generalización en el Capítulo 5.

Ejemplo\(\PageIndex{2}\)

Encuentra la serie de Fourier de la extensión periódica uniforme de la función\( f(t)= t^2\) para\( 0 \leq t \leq \pi\).

Solución

Queremos escribir\[ f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nt), \nonumber \] dónde\[ a_0= \frac{2}{\pi} \int_0^{\pi}t^2dt= \frac{2 \pi^2}{3}, \nonumber \] y

\[\begin{align}\begin{aligned} a_n &= \frac{2}{\pi} \int_0^{\pi}t^2 \cos(nt) dt= \frac{2 }{\pi} \left[ t^2 \frac{1}{n} \sin(nt)\right]_0^{\pi} - \frac{4}{n \pi} \int_0^{\pi} t \sin(nt)dt \\ &= \frac{4}{n^2 \pi} \left[ t \cos(nt)\right]_0^{\pi} + \frac{4}{n^2 \pi} \int_0^{\pi} \cos(nt)dt = \frac{4(-1)^n}{n^2}.\end{aligned}\end{align} \nonumber \]

Tenga en cuenta que hemos “detectado” la continuidad de la extensión ya que los coeficientes decaen como\(\frac{1}{n^2}\). Es decir, la extensión uniforme de\(t^2\) has no jump discontinuities. It does have corners, since the derivative, which is an odd function and a sine series, has jumps; it has a Fourier series whose coefficients decay only as \(\frac{1}{n}\).

De manera explícita, los primeros términos de la serie son

\[ \dfrac{\pi^2}{3}-4\cos{(t)}+\cos{(2t)} - \dfrac{4}{9}\cos{(3t)} + \cdots \nonumber \]

Ejercicio\(\PageIndex{3}\)

1. Calcular la derivada de la extensión par de\(f(t)\) arriba y verificar que tiene discontinuidades de salto. ¡Usa la definición real de\(f(t)\), no su serie coseno!
2. ¿Por qué es que la derivada de la extensión par de\(f(t)\) es la extensión impar de\(f'(t)\)?

Aplicación

Las series de Fourier se vinculan con los problemas de valor límite que estudiamos anteriormente. Veamos esta conexión con más detalle.

Supongamos que tenemos el problema del valor límite para\( 0<t <L\).

\[ x''(t) + \lambda x(t) = f(t), \nonumber \]

para las condiciones de contorno de Dirichlet\(x(0) = 0, x(L)=0\). Al utilizar la alternativa de Fredholm (Teorema 4.1.2) observamos que mientras no\(\lambda\) sea un valor propio del problema homogéneo subyacente, existe una solución única. Tenga en cuenta que las funciones propias de este problema de valores propios son las funciones\(\sin{\left(\frac{n\pi}{L}t\right)}\). Por lo tanto, para encontrar la solución, primero encontramos la serie sinusoidal de Fourier para\(f(t)\). Escribimos\(x\) también como una serie sinusoidal, pero con coeficientes desconocidos. Sustituimos la serie por\(x\) en la ecuación y resolvemos por los coeficientes desconocidos. Si tenemos las condiciones de límite de Neumann\(x'(0) = 0\) y\(x'(L)=0\), hacemos el mismo procedimiento usando la serie coseno.

Veamos cómo funciona este método en los ejemplos.

Ejemplo\(\PageIndex{3}\)

Tome el problema del valor límite para\(0<t<1\),

\[x''(t) + 2x(t) = f(t), \nonumber \]

donde\(f(t)=t\) en\(0<t<1\), y satisfaciendo las condiciones de frontera de Dirichlet\(x(0) = 0\) y\(x(1)=0\). Escribimos\(f(t)\) como una serie sinusoidal

\[ f(t) = \sum_{n=1}^{\infty} c_n \sin{(n\pi t)}. \nonumber \]

Compute

\[ c_n = 2\int_0^1 t\, \sin{(n\pi t)}\,dt = \dfrac{2(-1)^{n+1}}{n\pi}. \nonumber \]

Escribimos\(x(t)\) como

\[x(t)=\sum_{n=1}^{\infty} b_n \sin{(n\pi t)}. \nonumber \]

Nos enchufamos para obtener

\[\begin{align}\begin{aligned} x''(t) + 2 x(t) & = \underbrace{ \sum_{n=1}^\infty - b_n n^2 \pi^2 \sin (n \pi t) }_{x''} \, + \, 2 \underbrace{ \sum_{n=1}^\infty b_n \sin (n \pi t) }_{x} \\ & = \sum_{n=1}^\infty b_n (2 - n^2 \pi^2 ) \sin (n \pi t) \\ & = f(t) = \sum_{n=1}^\infty \frac{2\, {(-1)}^{n+1}}{n \pi} \sin (n \pi t) . \end{aligned}\end{align} \nonumber \]

Por lo tanto,\[ b_n (2-n^2\pi^2) = \dfrac{2(-1)^{n+1}}{n\pi} . \nonumber \] o\[ b_n = \dfrac{2(-1)^{n+1}}{n\pi(2-n^2\pi^2)} . \nonumber \]

Eso no\(2-n^{2}\pi ^{2}\) es cero para ninguno\(n\), y que podemos resolver\(b_{n}\), es precisamente porque no\(2\) es un valor propio del problema. Hemos obtenido así una serie de Fourier para la solución

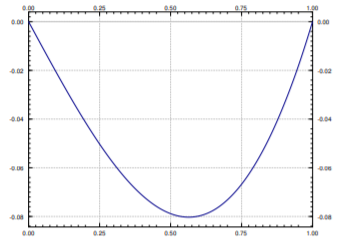
\[ x(t) = \sum_{n=1}^{\infty} \dfrac{2(-1)^{n+1}}{n\pi (2-n^2\pi^2)} \sin{(n\pi t)}. \nonumber \]

Ver Figura\(\PageIndex{2}\) para una gráfica de la solución. Observe que debido a que las funciones propias satisfacen las condiciones de contorno, y\(x\) se escriben en términos de las condiciones de límite, entonces\(x\) satisface las condiciones de límite.

Figura\(\PageIndex{2}\): Gráfica de la solución de\(x''+2x=t\),\(x(0)=0\),\(x(1)=0\).

Ejemplo\(\PageIndex{4}\)

De igual manera manejamos las condiciones de Neumann. Tome el problema del valor límite para\(0<t<1\),

\[x''(t) + 2x(t) = f(t), \nonumber \]

donde otra vez\(f(t)=t\) en\(0<t<1\), pero ahora satisfaciendo las condiciones fronterizas de Neumann\(x'(0) = 0\) y\(x'(1)=0\). Escribimos\(f(t)\) como serie coseno

\[ f(t) = \dfrac{c_0}{2} + \sum_{n=1}^{\infty} c_n\cos{(n\pi t)}, \nonumber \]

donde

\[ c_0=2\int_0^1 t \,dt =1 \nonumber \]

y

\[ c_n= 2 \int_0^1 t \cos(n \pi t)dt= \frac{2((-1)^n-1)}{\pi^2 n^2}= \left\{ \begin{array}{ccc} \frac{-4}{\pi^2 n^2} & \rm{if~} \it{n} \rm{~odd}, \\ 0 & \rm{if~} \it{n} \rm{~even}. \end{array} \right. \nonumber \]

También escribimos\(x(t)\) como serie coseno

\[ x(t) = \dfrac{a_0}{2} + \sum_{n=1}^{\infty} a_n\cos{(n\pi t)}. \nonumber \]

Nos enchufamos para obtener

\[\begin{align}\begin{aligned} x''(t)+2x(t) &= \sum_{n=1}^{\infty} \left[-a_n n^2 \pi^2 \cos(n \pi t) \right]+a_0+2 \sum_{n=1}^{\infty} \left[a_n \cos(n \pi t) \right] \\ &=a_0 + \sum_{n=1}^{\infty} a_n (2-n^2 \pi^2) \cos(n \pi t) \\ &= f(t)=\frac{1}{2}+ \sum_{\underset{n ~ odd}{n=1}}^{\infty} \frac{-4}{ \pi^2 n^2} \cos(n \pi t).\end{aligned}\end{align} \nonumber \]

Por lo tanto,\(a = \frac{1}{2}\) y\(a_n=0\) para\(n\) par (\(n \geq 2\)) y para\(n\) impar tenemos

\[ a_n(2-n^2\pi^2) = \dfrac{-4}{\pi^2n^2}, \nonumber \]

o

\[ a_n=\dfrac{-4}{n^2\,\pi^2(2-n^2\pi^2)}. \nonumber \]

La serie de Fourier para la solución\(x(t)\) es

\[ x(t)= \frac{1}{4}+ \sum_{\underset{n ~ odd}{n=1}}^{\infty} \frac{-4}{ n^2 \pi^2(2- n^2 \pi^2)} \cos(n \pi t). \nonumber \]