4.6: PDE, Separación de Variables y La Ecuación del Calor
- Page ID
- 115396
Recordemos que una ecuación diferencial parcial o PDE es una ecuación que contiene las derivadas parciales con respecto a varias variables independientes. La solución de PDEs será nuestra principal aplicación de las series de Fourier.
Se dice que una PDE es lineal si la variable dependiente y sus derivadas aparecen como máximo a la primera potencia y en ninguna función. Sólo hablaremos de PDE lineales. Junto con una PDE, generalmente hemos especificado algunas condiciones de límite, donde el valor de la solución o sus derivados se especifica a lo largo del límite de una región, y/o algunas condiciones iniciales donde el valor de la solución o sus derivadas se especifica por algún tiempo inicial. En ocasiones tales condiciones se mezclan entre sí y nos referiremos a ellas simplemente como condiciones laterales.
Estudiaremos tres ecuaciones diferenciales parciales específicas, cada una representando una clase más general de ecuaciones. Primero, estudiaremos la ecuación del calor, que es un ejemplo de una PDE parabólica. A continuación, estudiaremos la ecuación de onda, que es un ejemplo de una PDE hiperbólica. Finalmente, estudiaremos la ecuación de Laplace, que es un ejemplo de una PDE elíptica. Cada uno de nuestros ejemplos ilustrará un comportamiento que es típico de toda la clase.
Calor en un cable aislado
Primero estudiemos la ecuación del calor. Supongamos que tenemos un alambre (o una varilla metálica delgada) de longitud\(L\) que está aislado excepto en los puntos finales. Dejar\(x\) denotar la posición a lo largo del cable y dejar\(t\) denotar el tiempo. Ver Figura\(\PageIndex{1}\).
Dejar\(u(x,t)\) denotar la temperatura en punto\(x\) en el tiempo\(t\). La ecuación que rige esta configuración es la denominada ecuación de calor unidimensional:
\[\frac{\partial u}{\partial t} = k \frac{\partial^2 u}{\partial x^2}, \nonumber \]
donde\(k>0\) es una constante (la conductividad térmica del material). Es decir, el cambio de calor en un punto específico es proporcional a la segunda derivada del calor a lo largo del alambre. Esto tiene sentido; si a un fijo\(t\) la gráfica de la distribución de calor tiene un máximo (la gráfica es cóncava hacia abajo), entonces el calor fluye alejándose del máximo. Y viceversa.
Generalmente usaremos una notación más conveniente para las derivadas parciales. Escribiremos\(u_t\) en lugar de\( \frac{\partial u}{\partial t}\), y escribiremos\(u_{xx}\) en lugar de\(\frac{\partial^2 u}{\partial x^2} \). Con esta notación la ecuación de calor se convierte en
\[ u_t=ku_{xx}. \nonumber \]
Para la ecuación de calor, también debemos tener algunas condiciones de límite. Suponemos que los extremos del cable están expuestos y tocando algún cuerpo de calor constante, o bien los extremos están aislados. Por ejemplo, si los extremos del cable se mantienen a temperatura 0, entonces debemos tener las condiciones
\[ u(0,t)=0 \quad\text{and}\quad u(L,t)=0. \nonumber \]
Si, por otro lado, los extremos también están aislados obtenemos las condiciones
\[ u_x(0,t)=0 \quad\text{and}\quad u_x(L,t)=0. \nonumber \]
Veamos por qué es así. Si\(u_{x}\) es positivo en algún momento\(x_{0}\), entonces en un momento determinado,\(u\) es menor a la izquierda de\(x_{0}\), y más alto a la derecha de\(x_{0}\). El calor fluye de calor alto a calor bajo, es decir, a la izquierda. Por otro lado si\(u_{x}\) es negativo entonces el calor vuelve a fluir de calor alto a bajo calor, es decir a la derecha. Entonces, cuando\(u_{x}\) es cero, ese es un punto por el que no fluye el calor. En otras palabras,\(u_{x}(0,t)=0\) significa que no fluye calor dentro o fuera del cable en el punto\(x=0\).
Tenemos dos condiciones a lo largo del\(x\) eje ya que hay dos derivadas en la\(x\) dirección. Se dice que estas condiciones laterales son homogéneas (es decir,\(u\) o una derivada de\(u\) se establece en cero).
También necesitamos una condición inicial: la distribución de la temperatura en el momento\(t=0\). Es decir,
\[ u(x,0)=f(x), \nonumber \]
para alguna función conocida\(f(x)\). Esta condición inicial no es una condición lateral homogénea.
Separación de Variables
La ecuación de calor es lineal como\(u\) y sus derivadas no aparecen a ninguna potencia ni en ninguna función. Así, el principio de superposición todavía se aplica para la ecuación de calor (sin condiciones laterales). Si\(u_1\) y\(u_2\) son soluciones y\(c_1,c_2\) son constantes, entonces también\( u= c_1u_1+c_2u_2\) es una solución.
Verificar el principio de superposición para la ecuación de calor.
La superposición también conserva algunas de las condiciones laterales. En particular, si\(u_1\) y\(u_2\) son soluciones que satisfacen\(u(0,t)=0\) y\(u_(L,t)=0\), y\(c_1,\: c_2\) son constantes, entonces\( u= c_1u_1+c_2u_2\) sigue siendo una solución que satisface\(u(0,t)=0\) y\(u_(L,t)=0\). De igual manera para las condiciones laterales\(u_x(0,t)=0\) y\(u_x(L,t)=0\). En general, la superposición conserva todas las condiciones laterales homogéneas.
El método de separación de variables es tratar de encontrar soluciones que sean sumas o productos de funciones de una variable. Por ejemplo, para la ecuación del calor, tratamos de encontrar soluciones de la forma
\[ u(x,t)=X(x)T(t). \nonumber \]
Que la solución deseada que estamos buscando sea de esta forma es demasiado que esperar. Lo que es perfectamente razonable preguntar, sin embargo, es encontrar suficientes soluciones de “bloque de construcción” del formulario\( u(x,t)=X(x)T(t)\) utilizando este procedimiento para que la solución deseada a la PDE se construya de alguna manera a partir de estos bloques de construcción mediante el uso de superposición.
Tratemos de resolver la ecuación del calor
\[u_t=ku_{xx} \quad\text{with}\quad u(0,t)=0,\quad u(L,t)=0, \quad\text{and}\quad u(x,0)=f(x). \nonumber \]
Vamos a adivinar\(u(x,t)=X(x)T(t)\). Vamos a tratar de hacer que esta conjetura satisfaga la ecuación diferencial\(u_{t}=ku_{xx}\),, y las condiciones laterales homogéneas,\(u(0,t)=0\) y\(u(L,t)=0\). Entonces, a medida que la superposición preserva la ecuación diferencial y las condiciones laterales homogéneas, intentaremos construir una solución a partir de estos bloques de construcción para resolver la condición inicial no homogénea\(u(x,0)=f(x)\).
Primero nos conectamos\(u(x,t)=X(x)T(t)\) a la ecuación de calor para obtener
\[ X(x)T'(t)=kX''(x)T(t). \nonumber \]
Reescribimos como\[ \frac{T'(t)}{kT(t)}= \frac{X''(x)}{X(x)}. \nonumber \]
Esta ecuación debe sostenerse para todos\(x\) y para todos\(t\). Pero el lado izquierdo no depende\(x\) y el lado derecho no depende de\(t\). De ahí que cada lado debe ser una constante. Llamemos a esta constante\(- \lambda\) (el signo menos es por conveniencia más adelante). Obtenemos las dos ecuaciones
\[ \frac{T'(t)}{kT(t)}= - \lambda = \frac{X''(x)}{X(x)}. \nonumber \]
En otras palabras
\[\begin{align}\begin{aligned} X''(x) + \lambda X(x) &=0, \\ T'(t) + \lambda k T(t)& =0.\end{aligned}\end{align} \nonumber \]
La condición límite\(u(0,t)=0\) implica\( X(0)T(t)=0\). Estamos buscando una solución no trivial y así podemos asumir que no\(T(t)\) es idénticamente cero. De ahí\(X(0)=0\). De igual manera,\(u(L,t)=0\) implica\(X(L)=0\). Buscamos soluciones no triviales\(X\) del problema del valor propio\( X'' + \lambda X = 0, X(0)=0, X(L)=0\). Anteriormente hemos encontrado que los únicos valores propios son\( \lambda_n = \frac{n^2 \pi^2}{L^2}\), para los enteros\( n \geq 1\), donde están las funciones propias\( \sin \left( \frac{n \pi}{L}x \right)\). Por lo tanto, escojamos las soluciones
\[ X_n(x)= \sin \left( \frac{n \pi}{L}x \right). \nonumber \]
El correspondiente\(T_n\) debe satisfacer la ecuación
\[ T'_n(t) + \frac{n^2 \pi^2}{L^2}kT_n(t)=0. \nonumber \]
Por el método de factor integrador, la solución de este problema es
\[T_n(t)=e^{\frac{-n^2 \pi^2}{L^2}kt}. \nonumber \]
Será útil señalar eso\(T_n(0)=1\). Nuestras soluciones de bloques de construcción son
\[u_n(x,t)=X_n(x)T_n(t)= \sin \left( \frac{n \pi}{L}x \right) e^{\frac{-n^2 \pi^2}{L^2}kt}. \nonumber \]
Tomamos nota de eso\( u_n(x,0)= \sin \left( \frac{n \pi}{L}x \right)\). Escribamos\(f(x)\) como la serie sinusoidal
\[ f(x)= \sum_{n=1}^{\infty} b_n \sin \left( \frac{n \pi}{L}x \right). \nonumber \]
Es decir, encontramos la serie de Fourier de la extensión periódica impar de\(f(x)\). Se utilizó la serie sinusoidal ya que corresponde al problema del valor propio para\(X(x)\) arriba. Finalmente, utilizamos la superposición para escribir la solución como
\[ u(x,t)= \sum^{\infty}_{n=1}b_n u_n (x,t)= \sum^{\infty}_{n=1}b_n \sin \left(\frac{n \pi}{L}x \right)e^{\frac{-n^2 \pi^2}{L^2}kt}. \nonumber \]
¿Por qué funciona esta solución? Primero tenga en cuenta que es una solución a la ecuación de calor por superposición. Satisface\(u(0,t)=0\) y\(u(L,t)=0\), porque\(x=0\) o\(x=L\) hace desaparecer todos los senos. Por último, enchufando\(t=0\), notamos eso\(T_n(0)=1\) y así
\[ u(x,0)= \sum^{\infty}_{n=1}b_n u_n (x,0)= \sum^{\infty}_{n=1}b_n \sin \left(\frac{n \pi}{L}x \right)=f(x). \nonumber \]
Supongamos que tenemos un cable aislado de longitud\(1\), tal que los extremos del cable están incrustados en hielo (temperatura 0). Vamos\(k=0.003\). Entonces supongamos que la distribución inicial del calor es\(u(x,0)=50x(1-x)\). Ver Figura\(\PageIndex{2}\).
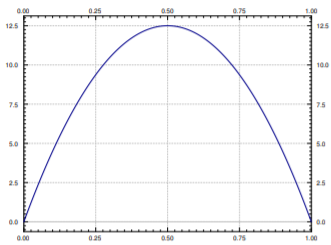
Queremos encontrar la función de temperatura\(u(x,t)\). Let us suppose we also want to find when (at what \(t\)) hace que la temperatura máxima en el cable caiga a la mitad del máximo inicial de\(12.5\).
Estamos resolviendo el siguiente problema de PDE:
\[\begin{align}\begin{aligned} u_t &=0.003u_{xx}, \\ u(0,t) &= u(1,t)=0, \\ u(x,0) &= 50x(1-x) ~~~~ {\rm{for~}} 0<x<1.\end{aligned}\end{align} \nonumber \]
Escribimos\(f(x)=50x(1-x)\) para\(0<x<1\) como una serie sinusoidal. Es decir,\(f(x)= \sum^{\infty}_{n=1}b_n \sin(n \pi x)\), donde
\[ b_n= 2 \int^1_0 50x(1-x) \sin(n \pi x)dx = \frac{200}{\pi^3 n^3}-\frac{200(-1)^n}{\pi^3 n^3}= \left\{ \begin{array}{cc} 0 & {\rm{if~}} n {\rm{~even,}} \\ \frac{400}{\pi^3 n^3} & {\rm{if~}} n {\rm{~odd.}} \end{array} \right. \nonumber \]
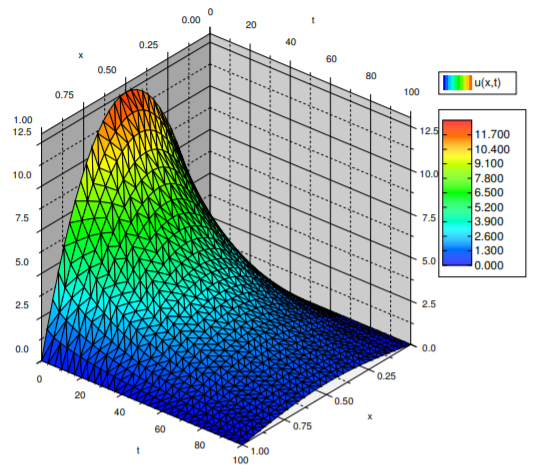
La solución\(u(x,t)\), plotted in Figure \(\PageIndex{3}\) for \( 0 \leq t \leq 100\), is given by the series:
\[ u(x,t)= \sum^{\infty}_{\underset{n~ {\rm{odd}} }{n=1}} \frac{400}{\pi^3 n^3} \sin(n \pi x) e^{-n^2 \pi^2 0.003t}. \nonumber \]
Por último, respondamos a la pregunta sobre la temperatura máxima. Es relativamente fácil ver que la temperatura máxima siempre estará en\(x=0.5\), en medio del cable. La trama de\(u(x,t)\) confirma esta intuición.
Si\(x=0.5\) enchufamos obtenemos
\[ u(0.5,t)= \sum^{\infty}_{\underset{n~ {\rm{odd}} }{n=1}} \frac{400}{\pi^3 n^3} \sin(n \pi 0.5) e^{-n^2 \pi^2 0.003t}. \nonumber \]
Para\(n=3\) y superior (recordar\(n\) es sólo impar), los términos de la serie son insignificantes en comparación con el primer término. El primer término de la serie ya es una muy buena aproximación de la función. De ahí
\[u(0.5,t) \approx \frac{400}{\pi^3}e^{-\pi^2 0.003t}. \nonumber \]
La aproximación mejora y mejora a medida que\(t\) se hace más grande a medida que los otros términos decaen mucho más rápido. Trazar la función\(0.5,t\), la temperatura en el punto medio del cable en el momento\(t\), en la Figura\(\PageIndex{4}\). La figura también traza la aproximación por el primer término.
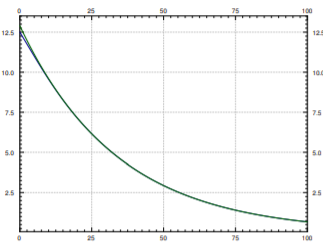
Después\(t=5\) or so it would be hard to tell the difference between the first term of the series for \(u(x,t)\) and the real solution \(u(x,t)\). This behavior is a general feature of solving the heat equation. If you are interested in behavior for large enough \(t\), only the first one or two terms may be necessary.
Volvamos a la pregunta de cuándo es la temperatura máxima la mitad de la temperatura máxima inicial. Es decir, cuando es la temperatura en el punto medio\(12.5/2=6.25\). Notamos en la gráfica que si utilizamos la aproximación por el primer término estaremos lo suficientemente cerca. Resolvemos
\[ 6.25=\frac{400}{\pi^3}e^{-\pi^2 0.003t}. \nonumber \]
Es decir,
\[ t=\frac{\ln{\frac{6.25 \pi^3}{400}}}{-\pi^2 0.003} \approx 24.5. \nonumber \]
Por lo que la temperatura máxima desciende a la mitad aproximadamente\(t=24.5\).
Mencionamos un comportamiento interesante de la solución a la ecuación de calor. La ecuación de calor “suaviza” la función a\(t\) medida\(f(x)\) que crece. Para un fijo\(t\), la solución es una serie de Fourier con coeficientes\(b_n e^{\frac{-n^2 \pi^2}{L^2}kt}\). Si\(t>0\), entonces estos coeficientes van a cero más rápido que cualquiera\(\frac{1}{n^P}\) para cualquier potencia\(p\). En otras palabras, la serie de Fourier tiene infinitamente muchos derivados en todas partes. Así incluso si la función\(f(x)\) tiene saltos y esquinas, entonces para un fijo\(t>0\), la solución\(u(x,t)\) en función de\(x\) es tan suave como queremos que sea.
Cuando la condición inicial ya es una serie sinusoidal, entonces no hay necesidad de computar nada, solo necesitas enchufarlo. Considera\[u_t = 0.3 \, u_{xx}, \qquad u(0,t)=u(1,t)=0, \qquad u(x,0) = 0.1 \sin(\pi t) + \sin(2\pi t) . \nonumber \] La solución es entonces\[u(x,t) = 0.1 \sin(\pi t) e^{- 0.3 \pi^2 t} + \sin(2 \pi t) e^{- 1.2 \pi^2 t} . \nonumber \]
Extremos aislados
Ahora supongamos que los extremos del cable están aislados. En este caso, estamos resolviendo la ecuación
\[ u_t=ku_{xx}\quad\text{with}\quad u_x(0,t)=0,\quad u_x(L,t)=0,\quad\text{and}\quad u(x,0)=f(x). \nonumber \]
Una vez más intentamos una solución de la forma\(u(x,t)=X(x)T(t)\). Por el mismo procedimiento que antes nos conectamos a la ecuación de calor y llegamos a las siguientes dos ecuaciones
\[\begin{align}\begin{aligned} X''(x)+\lambda X(x) &=0, \\ T'(t)+\lambda kT(t) &=0.\end{aligned}\end{align} \nonumber \]
En este punto la historia cambia ligeramente. La condición límite\(u_x(0,t)=0\) implica\(X'(0)T(t)=0\). De ahí\(X'(0)=0\). De igual manera,\(u_x(L,t)=0\) implica\(X'(L)=0\). Buscamos soluciones no triviales\(X\) del problema del valor propio\(X''+ \lambda X=0,\)\(X'(0)=0,\)\(X'(L)=0,\). Anteriormente hemos encontrado que los únicos valores propios son\(\lambda_n=\frac{n^2 \pi^2}{L^2}\), para los enteros\( n \geq 0\), donde están las funciones propias\(\cos(\frac{n \pi}{L})X\) (incluimos la función propia constante). Por lo tanto, escojamos soluciones
\[X_n(x)= \cos(\frac{n \pi}{L}x)\quad\text{and}\quad X_0(x)=1. \nonumber \]
El correspondiente\(T_n\) debe satisfacer la ecuación
\[T'_n(t)+ \frac{n^2 \pi^2}{L^2}kT_n(t)=0. \nonumber \]
Porque\(n \geq 1\), como antes,
\[T_n(t)= e^{\frac{-n^2 \pi^2}{L^2}kt}. \nonumber \]
Para\(n=0\), tenemos\(T'_0(t)=0\) y por lo tanto\(T_0(t)=1\). Nuestras soluciones de bloques de construcción serán
\[u_n(x,t)=X_n(x)T_n(t)= \cos \left( \frac{n \pi}{L} x \right) e^{\frac{-n^2 \pi^2}{L^2}kt}, \nonumber \]
y
\[u_0(x,t)=1. \nonumber \]
Tomamos nota de eso\(u_n(x,0) =\cos \left( \frac{n \pi}{L} x \right)\). Escribamos\(f\) usando la serie coseno
\[f(x)= \frac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \frac{n \pi}{L} x \right). \nonumber \]
Es decir, nos encontramos con la serie de Fourier de la extensión incluso periódica de\(f(x)\).
Utilizamos superposición para escribir la solución como
\[u(x,t)= \frac{a_0}{2} + \sum^{\infty}_{n=1} a_n u_n(x,t)= \frac{a_0}{2} + \sum^{\infty}_{n=1} a_n \cos \left( \frac{n \pi}{L} x \right) e^{\frac{-n^2 \pi^2}{L^2}kt}. \nonumber \]
Probemos la misma ecuación que antes, pero para extremos aislados. Estamos resolviendo el siguiente problema de PDE
\[\begin{align}\begin{aligned} u_t &=0.003u_{xx}, \\ u_x(0,t) &= u_x(1,t)=0, \\ u(x,0) &= 50x(1-x) ~~~~ {\rm{for~}} 0<x<1.\end{aligned}\end{align} \nonumber \]
Para este problema, debemos encontrar la serie coseno de\(u(x,0)\). Para\(0<x<1\) nosotros tenemos
\[ 50x(1-x)=\frac{25}{3}+\sum^{\infty}_{\underset{n~ {\rm{even}} }{n=2}} \left( \frac{-200}{\pi^2 n^2} \right) \cos(n \pi x). \nonumber \]
El cálculo se deja en manos del lector. De ahí que la solución al problema PDE, trazada en la Figura\(\PageIndex{5}\), viene dada por la serie
\[ u(x,t)=\frac{25}{3}+\sum^{\infty}_{\underset{n~ {\rm{even}} }{n=2}} \left( \frac{-200}{\pi^2 n^2} \right) \cos(n \pi x) e^{-n^2 \pi^2 0.003t}. \nonumber \]
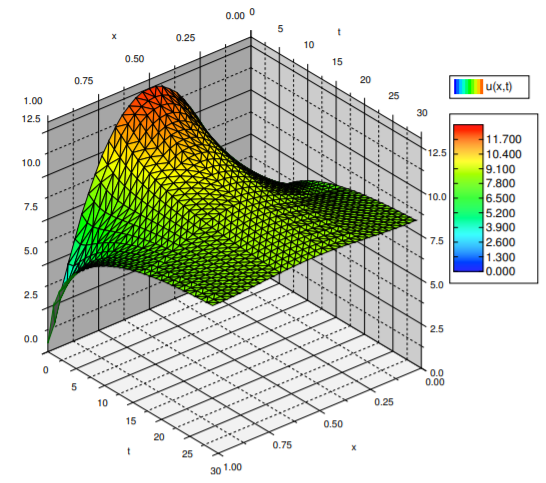
Observe en la gráfica que la temperatura se iguala a través del cable. Eventualmente, todos los términos excepto el constante se apagan, y te quedarás con una temperatura uniforme de\(\frac{25}{3} \approx{8.33}\) along the entire length of the wire.
Ampliemos sobre el último punto. El término constante en la serie es\[\frac{a_0}{2} = \frac{1}{L} \int_0^L f(x) \, dx . \nonumber \] En otras palabras,\(\frac{a_0}{2}\) es el valor promedio de\(f(x)\), es decir, el promedio de la temperatura inicial. Como el cable está aislado en todas partes, no puede salir calor, ningún calor puede entrar. Por lo que la temperatura trata de distribuirse uniformemente a lo largo del tiempo, y la temperatura media siempre debe ser la misma, en particular siempre lo es\(\frac{a_0}{2}\). A medida que el tiempo va al infinito, la temperatura va a la constante\(\frac{a_0}{2}\) en todas partes.


