4.7: Ecuación de Onda Unidimensional
- Page ID
- 115382
Imagina que tenemos una cuerda de guitarra tensada de longitud\(L\). Supongamos que solo consideramos vibraciones en una dirección. Es decir, vamos a\(x\) denotar la posición a lo largo de la cuerda, dejar\(t\) denotar el tiempo, y dejar\(y\) denotar el desplazamiento de la cuerda desde la posición de reposo. Ver Figura\(\PageIndex{1}\).
La ecuación que gobierna esta configuración es la llamada ecuación de onda unidimensional:
\[ y_{tt}=a^2 y_{xx}, \nonumber \]
para alguna constante\(a>0\). La intuición es similar a la ecuación del calor, reemplazando la velocidad por la aceleración: la aceleración en un punto específico es proporcional a la segunda derivada de la forma de la cuerda. En otras palabras, cuando la cuerda es cóncava hacia abajo entonces\(u_{xx}\) es negativa y la cuerda quiere acelerar hacia abajo, por lo que\(u_{tt}\) debería ser negativa. Y viceversa. La ecuación de onda es un ejemplo de una PDE hiperbólica.
Supongamos que los extremos de la cadena están fijos en su lugar:
\[y(0,t)=0 \quad\text{and}\quad y(L,t)=0. \nonumber \]
Tenga en cuenta que tenemos dos condiciones a lo largo del\(x\) eje ya que hay dos derivadas en la\(x\) dirección.
También hay dos derivadas a lo largo de la\(t\) dirección y por lo tanto necesitamos dos condiciones más aquí. Necesitamos conocer la posición inicial y la velocidad inicial de la cuerda. Es decir, para algunas funciones conocidas\(f(x)\) y\(g(x)\), imponemos
\[y(x,0)=f(x) \quad\text{and}\quad y_t(x,0)=g(x). \nonumber \]
Como la ecuación vuelve a ser lineal, la superposición funciona igual que lo hizo para la ecuación de calor. Y nuevamente usaremos la separación de variables para encontrar suficientes soluciones de bloques de construcción para obtener la solución general. Sin embargo, hay un cambio. Será más fácil resolver dos problemas separados y agregar sus soluciones.
Los dos problemas que resolveremos son
\[\label{wave:weq} \begin{array}{ll} w_{tt} = a^2 w_{xx} , & \\ w(0,t) = w(L,t) = 0 , & \\ w(x,0) = 0 & \qquad \text{for } \; 0 < x < L , \\ w_t(x,0) = g(x) & \qquad \text{for } \; 0 < x < L , \end{array} \]y\[\label{wave:zeq} \begin{array}{ll} z_{tt} = a^2 z_{xx} , & \\ z(0,t) = z(L,t) = 0 , & \\ z(x,0) = f(x) & \qquad \text{for } \; 0 < x < L , \\ z_t(x,0) = 0 & \qquad \text{for } \; 0 < x < L . \end{array} \]
El principio de superposición implica que\(y=w+z\) resuelve la ecuación de onda y además\( y(x,0)=w(x,0)+z(x,0)=f(x)\) y\( y_t(x,0)=w_t(x,0)+z_t(x,0)=g(x)\). Por lo tanto,\(y\) es una solución para
\[\label{wave:yeq} \begin{array}{ll} y_{tt} = a^2 y_{xx} , & \\ y(0,t) = y(L,t) = 0 , & \\ y(x,0) = f(x) & \qquad \text{for } \; 0 < x < L , \\ y_t(x,0) = g(x) & \qquad \text{for } \; 0 < x < L . \end{array} \]
La razón de toda esta complejidad es que la superposición sólo funciona para condiciones homogéneas como\(y(0,t)=y(L,t)=0\),\(y(x,0)=0\), o\(y_t(x,0)=0\). Por lo tanto, podremos utilizar la idea de separación de variables para encontrar muchas soluciones de bloques de construcción resolviendo todas las condiciones homogéneas. Luego podemos utilizarlos para construir una solución que resuelva la condición no homogénea restante.
Empecemos con\(\eqref{wave:weq}\). Intentamos de\(w(x,t)=X(x)T(t)\) nuevo una solución del formulario. Nos conectamos a la ecuación de onda para obtener
\[ X(x)T''(t)=a^2 X''(x)T(t). \nonumber \]
Reescribiendo obtenemos
\[ \dfrac{T''(t)}{a^2 T(t)}= \dfrac{X''(x)}{X(x)}. \nonumber \]
Nuevamente, el lado izquierdo depende solo de\(t\) y el lado derecho depende solo de\(x\). Por lo tanto, ambos equivalen a una constante, que denotaremos por\(- \lambda\).
\[ \dfrac{T''(t)}{a^2 T(t)}= - \lambda = \dfrac{X''(x)}{X(x)}. \nonumber \]
Resolvemos obtener dos ecuaciones diferenciales ordinarias
\[\begin{align}\begin{aligned} X''(x)+ \lambda X(x) &=0, \\ T''(t)+ \lambda a^2T(t) &=0.\end{aligned}\end{align} \nonumber \]
Las condiciones\(0=w(0,t)=X(0)T(t)\) lo implican\(X(0)=0\) e\(w(L,t)=0\) implican\(X(L)=0\). Por lo tanto, las únicas soluciones no triviales para la primera ecuación son cuándo\( \lambda = \lambda_n = \dfrac{n^2 \pi^2}{L^2}\) y son
\[ X_n(x)= \sin \left( \dfrac{n \pi}{L}x \right). \nonumber \]
La solución general\(T\) para este particular\( \lambda_n \) es
\[ T_n(t)= A \cos \left( \dfrac{n \pi a}{L}t \right) + B \sin \left( \dfrac{n \pi a}{L}t \right) . \nonumber \]
También tenemos la condición de que\(w(x,0)=0\) o\(X(x)T(0)=0\). Esto implica eso\(T(0)=0\), que a su vez obliga\(A=0\). Es conveniente escoger\(B= \dfrac{L}{n \pi a}\) (verás por qué en un momento) y por lo tanto
\[ T_n(t)= \dfrac{L}{n \pi a} \sin \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Nuestras soluciones de bloques de construcción son
\[ w_n(x,t)= \dfrac{L}{n \pi a} \sin \left( \dfrac{n \pi }{L}x \right) \sin \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Nos diferenciamos en\(t\), es decir
\[ \dfrac{\partial w_n}{\partial t}(x,t)= \sin \left( \dfrac{n \pi }{L}x \right) \cos \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Por lo tanto,
\[ \dfrac{\partial w_n}{\partial t}(x,0)= \sin \left( \dfrac{n \pi }{L}x \right) . \nonumber \]
Nos expandimos\(g(x)\) en términos de estos senos como
\[ g(x)= \sum_{n=1}^{\infty} b_n \sin \left( \dfrac{n \pi}{L}x \right). \nonumber \]
Usando superposición podemos simplemente anotar la solución\(\eqref{wave:weq}\) como una serie
\[ w(x,t)= \sum_{n=1}^{\infty} b_n w_n(x,t) = \sum_{n=1}^{\infty} b_n \dfrac{L}{n \pi a} \sin \left( \dfrac{n \pi }{L}x \right) \sin \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Verifica eso\(w(x,0)=0\) y\(w_t(x,0)=g(x)\).
De igual manera procedemos a resolver\(\eqref{wave:zeq}\). Volvemos a intentarlo\(z(x,y)=X(x)T(t)\). El procedimiento funciona exactamente igual al principio. Obtenemos
\[\begin{align}\begin{aligned} X''(x)+ \lambda X(x) &=0, \\ T''(t)+ \lambda a^2T(t) &=0.\end{aligned}\end{align} \nonumber \]
y las condiciones\(X(0)=0\),\(X(L)=0\). Así que de nuevo\( \lambda = \lambda_n = \dfrac{n^2 \pi^2}{L^2}\) y
\[ X_n(x)= \sin \left( \dfrac{n \pi}{L}x \right). \nonumber \]
Esta vez la condición en\(T\) es\(T'(0)=0\). Así lo conseguimos\(B=0\) y tomamos
\[ T_n(t)= \cos \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Nuestra solución de bloque de construcción será
\[ z_n(x,t)= \sin \left( \dfrac{n \pi}{L}x \right) \cos \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Como\(z_{n}(x,0)=\sin\left(\frac{n\pi}{L}x\right)\), nos expandimos\(f(x)\) en términos de estos senos como
\[ f(x)= \sum_{n=1}^{\infty}c_n \sin \left( \dfrac{n \pi}{L}x \right). \nonumber \]
Y escribimos la solución a\(\eqref{wave:zeq}\) como una serie
\[ z(x,t)= \sum_{n=1}^{\infty}c_n z_n (x,t)= \sum_{n=1}^{\infty} c_n \sin \left( \dfrac{n \pi}{L}x \right) \cos \left( \dfrac{n \pi a}{L}t \right). \nonumber \]
Rellene los datos en la derivación de la solución de\(\eqref{wave:zeq}\). Verifique que la solución satisfaga todas las condiciones laterales.
Armando estas dos soluciones, expongamos el resultado como teorema.
Toma la ecuación
\[\label{wave:tyeq} \begin{array}{ll} y_{tt} = a^2 y_{xx} , & \\ y(0,t) = y(L,t) = 0 , & \\ y(x,0) = f(x) & \qquad \text{for } \; 0 < x < L , \\ y_t(x,0) = g(x) & \qquad \text{for } \; 0 < x < L , \end{array} \]
donde
\[ f(x)= \sum_{n=1}^{\infty} c_n \sin \left( \dfrac{n \pi}{L}x \right), \nonumber \]
y
\[ g(x)= \sum_{n=1}^{\infty} b_n \sin \left( \dfrac{n \pi}{L}x \right). \nonumber \]
Entonces la solución se\( y(x,t)\) puede escribir como una suma de las soluciones de (4.7.4) y (4.7.5). En otras palabras,
\[\begin{align}\begin{aligned} y(x,t) &= \sum_{n=1}^{\infty} b_n \dfrac{L}{n \pi a} \sin \left( \dfrac{n \pi}{L}x \right) \sin \left( \dfrac{n \pi a}{L}t \right) + c_n \sin \left( \dfrac{n \pi}{L}x \right) \cos \left( \dfrac{n \pi a}{L}t \right) \\ &= \sum_{n=1}^{\infty} \sin \left( \dfrac{n \pi}{L}x \right) \left[ b_n \dfrac{L}{n \pi a} \sin \left( \dfrac{n \pi a}{L}t \right) +c_n \cos \left( \dfrac{n \pi a}{L}t \right) \right].\end{aligned}\end{align} \nonumber \]
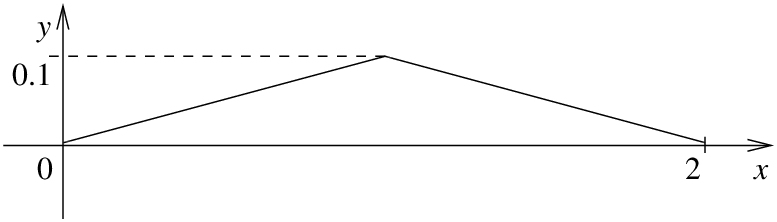
Probemos un ejemplo sencillo de una cuerda arrancada. Supongamos que una cuerda de longitud 2 es arrancada en el medio de tal manera que tenga la forma inicial dada en la Figura\(\PageIndex{2}\). Eso es
\[ f(x)= \left\{ \begin{array}{cc} 0.1x & {\rm{if}}~ 0 \leq x \leq 1, \\ 0.1(2-x) & {\rm{if}}~ 1 < x \leq 2 \end{array} \right. . \nonumber \]
La cadena comienza en rest (\(g(x)=0\)). Supongamos que\(a=1\) en la ecuación de onda por simplicidad. En otras palabras, deseamos resolver el problema:
\[\begin{align}\begin{aligned} & y_{tt} = y_{xx}, \\ & y(0,t) = y(2,t)= 0 , \\ & y(x,0) = f(x) \quad \text{and} \quad y_t(x,0)= 0 .\end{aligned}\end{align} \nonumber \]
Dejamos al lector computar la serie sinusoidal de\(f(x)\). The series will be
\[f(x)= \sum_{n=1}^{\infty} \dfrac{0.8}{n^2 \pi^2} \sin \left( \dfrac{n \pi}{2} \right) \sin \left( \dfrac{n \pi}{2} x \right). \nonumber \]
Tenga en cuenta que\( \sin \left( \dfrac{n \pi}{2} \right) \) es la secuencia\(1,0,-1,0,1,0,-1, \ldots\) para\(n=1,2,3,4, \ldots\). Por lo tanto,
\[ f(x)= \dfrac{0.8}{ \pi^2} \sin \left( \dfrac{\pi}{2}x \right) - \dfrac{0.8}{9 \pi^2} \sin \left( \dfrac{3 \pi}{2}x \right) + \dfrac{0.8}{25 \pi^2} \sin \left( \dfrac{5 \pi}{2}x \right) - \cdots \nonumber \]
La solución\(y(x,t)\) viene dada por
\[\begin{align}\begin{aligned} y(x,t) & = \sum_{n=1}^\infty \frac{0.8}{n^2 \pi^2} \sin \left( \frac{n \pi}{2} \right) \sin \left( \frac{n \pi}{2} x \right) \cos \left( \frac{n \pi}{2} t \right) \\ & = \sum_{m=1}^\infty \frac{0.8 {(-1)}^{m+1}}{{(2m-1)}^2 \pi^2} \sin \left( \frac{(2m-1) \pi}{2} x \right) \cos \left( \frac{(2m-1) \pi}{2} t \right) \\ & = \frac{0.8}{\pi^2} \sin \left( \frac{\pi}{2} x \right) \cos \left( \frac{\pi}{2} t \right) - \frac{0.8}{9 \pi^2} \sin \left( \frac{3 \pi}{2} x \right) \cos \left( \frac{3 \pi}{2} t \right) \\ & \hspace{20em} + \frac{0.8}{25 \pi^2} \sin \left( \frac{5 \pi}{2} x \right) \cos \left( \frac{5 \pi}{2} t \right) - \cdots \end{aligned}\end{align} \nonumber \]
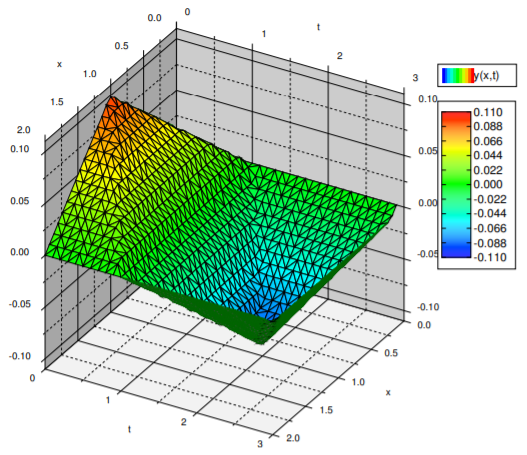
Ver Figura\(\PageIndex{3}\) para una gráfica para\(0 < t < 3\). Observe que a diferencia de la ecuación de calor, la solución no se vuelve “más suave”, los “bordes afilados” permanecen. Veremos el motivo de este comportamiento en la siguiente sección donde derivamos la solución a la ecuación de onda de una manera diferente.
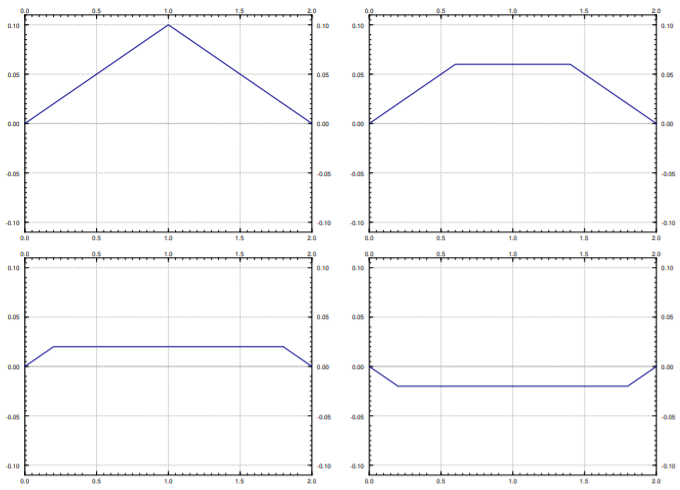
Asegúrate de entender lo que te está diciendo la trama, como la de la figura. Para cada fijo\(t\), se puede pensar en la función\(y(x,t)\) como solo una función de\(x\). Esta función te da la forma de la cadena a la vez\(t\). Ver Figura\(\PageIndex{4}\) para gráficas de at en\(y\) función de\(x\) a varios valores diferentes de\(t\). En esta parcela se pueden ver los bordes afilados permaneciendo mucho mejor.
Una cosa que hay que quitar de todo esto es cómo suena una guitarra. Observe que las frecuencias (angulares) que surgen en la solución son\(n \frac{\pi a}{L}\). Es decir, hay una cierta frecuencia fundamental base\(\frac{\pi a}{L}\), y luego también obtenemos todos los múltiplos de esta frecuencia, que en la música se llaman los armónicos. Qué armónicos aparecen y con qué amplitud es lo que los músicos llaman el timbre de la nota. Los matemáticos suelen llamar a esto el espectro. Debido a que todas las frecuencias son múltiplos de una frecuencia (la fundamental) obtenemos un agradable sonido agradable.
La frecuencia fundamental\(\frac{\pi a}{L}\) aumenta a medida que disminuimos la longitud\(L\). Es decir, si colocamos un dedo en el diapasón y luego arrancamos una cuerda obtenemos una nota más alta. La constante\(a\) viene dada por\[a = \sqrt{\frac{T}{\rho}} , \nonumber \] donde\(T\) está la tensión y\(\rho\) es la densidad lineal de la cuerda. Apretar la cuerda (girar la clavija de afinación en una guitarra) aumenta\(a\) y por lo tanto produce una frecuencia fundamental más alta (una nota más alta). Por otro lado el uso de una cuerda más pesada reduce\(a\) y produce una frecuencia fundamental más baja (una nota más baja). Un bajo tiene cuerdas más largas y gruesas, mientras que un ukelele tiene cuerdas cortas hechas de material más ligero.
Algo bastante interesante es la casi simetría entre el espacio y el tiempo. En su forma más simple vemos esta simetría en las soluciones\[\sin \left( \frac{n \pi}{L} x \right) \sin \left( \frac{n \pi a}{L} t \right) . \nonumber \] Excepto por el\(a\), el tiempo y el espacio son lo mismo.
En general, la solución para un fijo\(x\) es una serie de Fourier en\(t\), para una fija\(t\) es una serie de Fourier en\(x\), y los coeficientes están relacionados. Si la forma\(f(x)\) o la velocidad inicial tienen muchas esquinas, entonces la onda sonora tendrá muchas esquinas. Esto se debe a que los coeficientes de Fourier de la forma inicial decaen a cero (as\(n \to \infty\)) a la misma velocidad que los coeficientes de Fourier de la onda en el tiempo (para algunos fijos\(x\)). Entonces, si usas un objeto afilado para escoger la cuerda, obtienes un sonido más nítido con muchos componentes de alta frecuencia, mientras que si usas tu pulgar, obtienes un sonido más suave sin tantos armónicos altos. De igual manera si arrancas cerca del puente, estás recibiendo un desplumón que se parece más al diente de sierra, y obtienes un sonido aún más nítido.
De hecho, si miras la fórmula para la solución, ves que para cualquier fijo\(x\) obtenemos una serie de Fourier casi arbitraria en\(t\), todo excepto el término constante. Esencialmente puedes obtener cualquier sonido que quieras arrancando la cuerda de la manera correcta. Por supuesto que estamos considerando una cuerda ideal sin rigidez y sin resistencia al aire. Esas variables impactan claramente también en el sonido.


