4.8: Solución D'Alembert de La Ecuación de Onda
- Page ID
- 115403
Hemos resuelto la ecuación de onda usando series de Fourier. Pero a menudo es más conveniente utilizar la llamada solución d'Alembert a la ecuación de onda. \(^{1}\)Si bien esta solución también se puede derivar usando series de Fourier, es realmente un uso incómodo de esos conceptos. Es más fácil e instructivo derivar esta solución haciendo un cambio correcto de variables para obtener una ecuación que pueda resolverse mediante una simple integración.
Supongamos que tenemos la ecuación de onda
\[\label{eq:1} y_{tt}=a^2 y_{xx}. \]
Deseamos resolver la ecuación\(\eqref{eq:1}\) dadas las condiciones
\[ \begin{align} y(0,t) &= y(L,t) = 0 & & \text{for all } t ,\nonumber \\ y(x,0) &= f(x) & & 0 < x < L , \label{eq:2} \\ y_t(x,0) &= g(x) & & 0 < x < L . \end{align} \nonumber \]
Cambio de Variables
Transformaremos la ecuación en una forma más simple donde se pueda resolver mediante una simple integración. Cambiamos las variables a\( \xi =x-at\),\( \eta =x+at\). La regla de la cadena dice:
\[\begin{align}\begin{aligned} \frac{\partial}{\partial x} &= \frac{\partial \xi}{\partial x} \frac{\partial}{\partial \xi}+\frac{\partial \eta}{\partial x}\frac{\partial}{\partial \eta}= \frac{\partial}{\partial \xi}+ \frac{\partial}{\partial \eta}, \\ \frac{\partial}{\partial t} &= \frac{\partial \xi}{\partial t}\frac{\partial}{\partial \xi}+\frac{\partial \eta}{\partial t}\frac{\partial}{\partial \eta}= -a \frac{\partial}{\partial \xi} + a\frac{\partial}{\partial \eta}.\end{aligned}\end{align} \nonumber \]
Nosotros computamos
\[\begin{align}\begin{aligned} y_{xx} &= \frac{\partial^2 y}{\partial x^2}= \left( \frac{\partial}{\partial \xi}+ \frac{\partial}{\partial \eta} \right) \left( \frac{\partial y}{\partial \xi}+ \frac{\partial y}{\partial \eta} \right)= \frac{\partial^2 y}{\partial \xi^2}+2 \frac{\partial^2 y}{\partial \xi \partial \eta}+ \frac{\partial^2 y}{\partial \eta^2}, \\ y_{tt} &= \frac{\partial^2 y}{\partial ^2}= \left( -a \frac{\partial}{\partial \xi}+a \frac{\partial}{\partial \eta} \right) \left( -a \frac{\partial y}{\partial \xi}+ a \frac{\partial y}{\partial \eta} \right)= a^2 \frac{\partial^2 y}{\partial \xi^2}-2a^2 \frac{\partial^2 y}{\partial \xi \partial \eta}+a^2 \frac{\partial^2 y}{\partial \eta^2}. \end{aligned}\end{align} \nonumber \]
En los cálculos anteriores, se utilizó el hecho del cálculo que\( \frac{\partial^2 y}{\partial \xi \partial \eta}=\frac{\partial^2 y}{\partial \eta \partial \xi}\). Tapamos lo que nos metimos en la ecuación de onda,
\[ 0=a^2 y_{xx}-y_{tt}=4a^2 \frac{\partial^2 y}{\partial \xi \partial \eta}= 4a^2 y_{ \xi \eta}. \nonumber \]
Por lo tanto, la ecuación de onda\(\eqref{eq:1}\) se transforma en\( y_{ \xi \eta} =0 \). Es fácil encontrar la solución general a esta ecuación integrando dos veces. \( \xi\)Manteniéndonos constantes, nos integramos con respecto a\( \eta\) primero \(^{2}\)y notamos de que depende la constante de integración\( \xi\); para cada uno\( \xi\) podríamos obtener una constante de integración diferente. Obtenemos\(y _{ \xi}=C( \xi)\). A continuación, nos integramos con respecto\( \xi\) y notamos de que la constante de integración debe depender\( \eta\). Así,\( y= \int C( \xi)d \xi+B( \eta) \). La solución debe, por lo tanto, ser de la siguiente forma para algunas funciones\(A( \xi)\) y\(B( \eta ) \):
\[ y =A( \xi)+B( \eta)= A(x-at)+B(x+at). \nonumber \]
La solución es una superposición de dos funciones (ondas) que viajan a velocidad\(a\) en direcciones opuestas. Las coordenadas\(\xi\) y\(\eta\) se denominan las coordenadas características, y una técnica similar se puede aplicar a la PDE hiperbólica más complicada. Y de hecho, en la Sección 1.9 se utiliza para resolver PDE lineal de primer orden. Básicamente, para resolver la ecuación de onda (o ecuaciones hiperbólicas más generales) encontramos ciertas curvas características a lo largo de las cuales la ecuación es realmente solo una ODE, o un par de ODEs. En este caso estas son las curvas donde\(\xi\) y\(\eta\) son constantes.
Fórmula de D'Alembert
Sabemos cómo debe ser cualquier solución, pero tenemos que resolver para las condiciones laterales dadas. Simplemente vamos a dar la fórmula y ver que funciona. Primero vamos a\( F(x)\) denotar la extensión impar de\( f(x)\), y dejar\( G(x)\) denotar la extensión impar de\( g(x)\). Definir
\[ A(x)= \frac{1}{2} F(x)- \frac{1}{2a} \int^x_0 G(s) ds,\quad B(x)= \frac{1}{2} F(x)+ \frac{1}{2a} \int^x_0 G(s) ds. \nonumber \]
Nosotros lo reclamamos\( A(x)\) y\( B(x)\) damos la solución. De manera explícita, la solución es\(y(x,t)= A(x-at)+B(x+at)\) o en otras palabras:
\[ \begin{align} y(x,t) &= \frac{1}{2}F(x-at)- \frac{1}{2a} \int_0^{x-at} G(s)ds+ \frac{1}{2}F(x+at)+ \frac{1}{2a} \int_0^{x+at} G(s)ds \label{eq:8} \\ &= \frac{F(x-at)+F(x+at)}{2} + \frac{1}{2a} \int_{x-at}^{x+at} G(s)ds. \end{align} \nonumber \]
Comvisemos que la fórmula de d'Alembert realmente funciona.
\[ y(x,0)= \frac{1}{2}F(x)- \frac{1}{2a} \int_0^{x} G(s)ds+ \frac{1}{2}F(x)+ \frac{1}{2a} \int_0^{x} G(s)ds =F(x). \nonumber \]
Hasta el momento tan bueno. Asumir por simplicidad\(F\) es diferenciable. Y usamos la primera forma de\(\eqref{eq:8}\) ya que es más fácil de diferenciar. Por el teorema fundamental del cálculo tenemos
\[ y_t(x,t)= \frac{-a}{2}F'(x-at)+ \frac{1}{2}G(x-at)+ \frac{a}{2} F'(x+at)+ \frac{1}{2}G(x+at). \nonumber \]
Entonces
\[ y_t(x,0)= \frac{-a}{2}F'(x)+ \frac{1}{2}G(x)+ \frac{a}{2} F'(x)+ \frac{1}{2}G(x)=G(x). \nonumber \]
¡Yay! Ahora estamos fumando. Bien, ahora las condiciones de contorno. Tenga en cuenta que\(F(x)\) y\(G(x)\) son impares. También\( \int_0^x G(s)ds\) es una función par de\(x\) porque\(G(x)\) es impar (para ver este hecho, hacer la sustitución\(s=-v\)). Entonces
\[\begin{align}\begin{aligned} y(0,t) &= \frac{1}{2}F(-at)- \frac{1}{2a} \int_0^{-at} G(s)ds+ \frac{1}{2}F(at)+ \frac{1}{2a} \int_0^{at} G(s)ds \\ &= \frac{-1}{2}F(at)- \frac{1}{2a} \int_0^{at} G(s)ds+ \frac{1}{2}F(at)+ \frac{1}{2a} \int_0^{at} G(s)ds=0 .\end{aligned}\end{align} \nonumber \]
Tenga en cuenta que\(F(x)\) y\(G(x)\) son\(2L\) periódicos. Nosotros computamos
\[\begin{align}\begin{aligned} y(L,t) &= \frac{1}{2}F(L-at)- \frac{1}{2a} \int_0^{L-at} G(s)ds+ \frac{1}{2}F(L+at)+ \frac{1}{2a} \int_0^{L+at} G(s)ds \\ &= \frac{1}{2}F(-L-at)- \frac{1}{2a} \int_0^{L} G(s)ds- \frac{1}{2a} \int_0^{-at} G(s)ds +\\ &= \frac{1}{2}F(L+at)+ \frac{1}{2a} \int_0^{L} G(s)ds+ \frac{1}{2a} \int_0^{at} G(s)ds \\ &= \frac{-1}{2}F(L+at)- \frac{1}{2a} \int_0^{at} G(s)ds+ \frac{1}{2}F(L+at)+ \frac{1}{2a} \int_0^{at} G(s)ds=0.\end{aligned}\end{align} \nonumber \]
Y voilà, funciona.
D'Alembert dice que la solución es una superposición de dos funciones (ondas) que se mueven en sentido contrario a “velocidad”\(a\). Para hacernos una idea de cómo funciona, vamos a elaborar un ejemplo. Considere la configuración más simple
\[\begin{align}\begin{aligned} y_{tt} &=y_{xx}, \\ y(0,t) &=y(1,t)=0, \\ y(x,0) & =f(x), \\ y_t(x,0) & =0.\end{aligned}\end{align} \nonumber \]
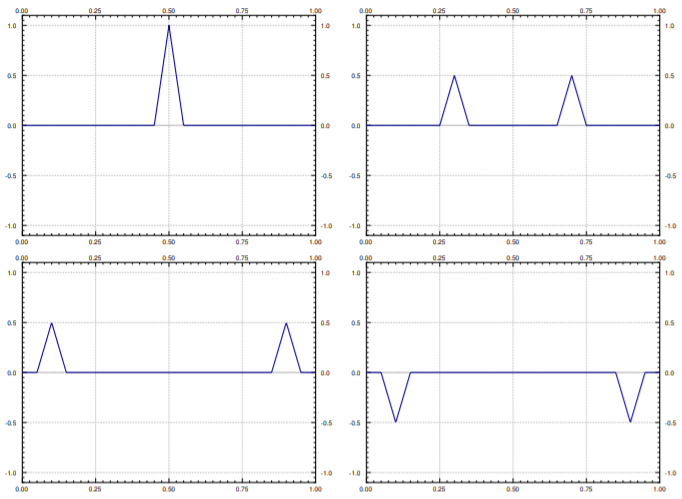
Aquí\(f(x)\) hay un impulso de altura 1 centrado en\(x=0.5\):
\[ f(x) = \left\{ \begin{array}{ccc} 0 & {\rm{if}} & 0 \leq x < 0.45, \\ 20(x-0.45) & {\rm{if}} & 0.45 \leq x < 0.5, \\ 20(0.55-x) & {\rm{if}} & 0.5 \leq x < 0.55 \\ 0 & {\rm{if}} & 0.55 \leq x \leq 1. \end{array} \right. \nonumber \]
La gráfica de este impulso es la gráfica superior izquierda en la Figura\(\PageIndex{1}\).
Dejado\(F(x)\) ser la extensión periódica impar de\(f(x)\). Entonces de\(\eqref{eq:8}\) sabemos que la solución se da como
\[ y(x,t)= \frac{F(x-t)+F(x+t)}{2}. \nonumber \]
No es difícil calcular valores específicos de\( y(x,t)\). Por ejemplo, para computar\(y(0.1,0.6)\) notamos\(x-t=-0.5\) y\(x+t=0.7\). Ahora\(F(-0.5)=-f(0.5)=-20(0.55-0.5)=-1\) y\(F(0.7)=f(0.7)=0\). De ahí\(y(0.1,0.6)= \frac{-1+0}{2}=-0.5\). Como puede ver, la solución d'Alembert es mucho más fácil de calcular y de trazar que la solución de la serie de Fourier. Ver Figura\(\PageIndex{1}\) para gráficas de la solución\(y\) para varios diferentes\(t\).
Otra forma de resolver las condiciones secundarias
Quizás sea más fácil y más útil memorizar el procedimiento en lugar de la propia fórmula. Lo importante a recordar es que una solución a la ecuación de onda es una superposición de dos ondas que viajan en direcciones opuestas. Es decir,
\[y(x,t)=A(x-at)+B(x+at). \nonumber \]
Si lo piensas, las fórmulas exactas para\(A\) y no\(B\) son difíciles de adivinar una vez que te das cuenta de qué tipo de condiciones secundarias\(y(x,t)\) se supone que deben satisfacer. Demos de nuevo la fórmula, pero ligeramente diferente. El mejor enfoque es hacer esto por etapas. Cuando\(g(x)=0\) (y por lo tanto\(G(x)=0\)) tenemos la solución
\[ \frac{F(x-at)+F(x+at)}{2}. \nonumber \]
Por otro lado, cuando\(f(x)=0\) (y por lo tanto\(F(x)=0\)), dejamos
\[H(x)=\int_0^x G(s)ds. \nonumber \]
La solución en este caso es
\[\frac{1}{2a} \int_{x-at}^{x+at} G(s)ds = \frac{-H(x-at)+H(x+at)}{2a}. \nonumber \]
Por superposición obtenemos una solución para las condiciones laterales generales\(\eqref{eq:2}\) (cuando\(f(x)\) ni ni\(g(x)\) son idénticamente cero).
\[\label{eq:21} y(x,t)= \frac{F(x-at)+F(x+at)}{2} + \frac{-H(x-at)+H(x+at)}{2a}. \]
Anote el signo menos antes del\(H\), y el\(a\) en el segundo denominador.
Verifique que la nueva fórmula\(\eqref{eq:21}\) satisfaga las condiciones laterales\(\eqref{eq:2}\).
Advertencia: Asegúrese de usar las extensiones impares\(F(x)\) y\(G(x)\), cuando tenga fórmulas para\(f(x)\) y\(g(x)\). El caso es, esas fórmulas en general se mantienen sólo para\(0<x<L\), y no suelen ser iguales a\(F(x)\) y\(G(x)\) para otras\(x\).
Observaciones
Comentemos que la fórmula\(y(x,t) = A(x-at) + B(x+at)\) es la razón por la que la solución de la ecuación de onda no llega a medida que pasa el tiempo, es decir, por qué en los ejemplos donde las condiciones iniciales tenían esquinas, la solución también tiene esquinas en cada momento\(t\).
Los rincones nos llevan a otra observación interesante. Nadie se da cuenta nunca al principio que nuestras soluciones de ejemplo ni siquiera son diferenciables (tienen esquinas): En Ejemplo\(\PageIndex{1}\) anterior, la solución no es diferenciable cuando sea\(x=t+0.5\) o\(x=-t+0.5\) por ejemplo. Realmente para poder computar\(u_{xx}\) o\(u_{tt}\), no necesitas uno, sino dos derivados. No temas, podríamos pensar en una forma que está muy cerca\(F(x)\) pero que tiene dos derivadas al redondear un poco las esquinas, y entonces la solución estaría muy cerca\(\frac{F(x-t)+F(x+t)}{2}\) y nadie se daría cuenta del interruptor.
Una última observación es lo que nos dice la solución de d'Alembert sobre qué parte de las condiciones iniciales influyen en la solución en un momento determinado. Podemos resolverlo por Supongamos que la cuerda es muy larga (quizás infinita) por simplicidad. Ya que la solución en el momento\(t\) es que\[y(x,t) = \frac{F(x-at) + F(x+at)}{2} + \frac{1}{2a} \int_{x-at}^{x+at} G(s) \,ds , \nonumber \] notamos que solo hemos usado las condiciones iniciales en el intervalo\([x-at,x+at]\). Estos dos puntos finales se llaman los frentes de onda, ya que es ahí donde se le da al frente de onda una perturbación inicial (\(t=0\)) en\(x\). Entonces si\(a=1\), un observador sentado en\(x=0\) su momento solo\(t=1\) ha visto las condiciones iniciales para\(x\) dentro del rango\([-1,1]\) y es dichosamente inconsciente de nada más. Es por ello que, por ejemplo, no sabemos que una supernova ha ocurrido en el universo hasta que vemos su luz, millones de años desde el momento en que efectivamente sucedió.
Notas al pie
[1] Nombrado así por el matemático francés Jean le Rond d'Alembert (1717 — 1783).
[2] No hay nada de especial en\(\eta\), puedes integrarte\(\xi\) primero, si lo deseas.


