4.9: La temperatura de estado estacionario y el laplaciano
- Page ID
- 115348
Supongamos que tenemos un cable aislado, una placa o un objeto tridimensional. Aplicamos ciertas temperaturas fijas en los extremos del alambre, los bordes de la placa, o en todos los lados del objeto tridimensional. Deseamos conocer cuál es la distribución de temperatura en estado estacionario. Es decir, deseamos saber cuál será la temperatura después de un periodo de tiempo suficientemente largo.
Realmente estamos buscando una solución a la ecuación del calor que no dependa del tiempo. Primero resolvamos el problema en una variable de espacio. Buscamos una función\(u\) que satisfaga
\[u_t=ku_{xx}, \nonumber \]
pero tal que\(u_t=0\) para todos\(x\) y\(t\). De ahí que estemos buscando una función de\(x\) solo que satisfaga\(u_{xx}=0\). Es fácil resolver esta ecuación por integración y vemos que\(u=Ax+B\) para algunas constantes\(A\) y\(B\).
Supongamos que tenemos un cable aislado, y aplicamos\(T_1\) temperatura constante en un extremo (digamos dónde\(x=0\)) y\(T_2\) en el otro extremo (en\(x=L\) donde\(L\) está la longitud del cable). Entonces nuestra solución de estado estacionario es
\[u(x)= \dfrac{T_2-T_1}{L}x+T_1. \nonumber \]
Esta solución concuerda con nuestra intuición de sentido común con cómo se debe distribuir el calor en el alambre. Entonces, en una dimensión, las soluciones de estado estacionario son básicamente líneas rectas.
Las cosas son más complicadas en dos o más dimensiones espaciales. Vamos a restringirnos a dos dimensiones espaciales por simplicidad. La ecuación de calor en dos variables de espacio es
\[\label{eq:3} u_t=k(u_{xx}+u_{yy}), \]
o más comúnmente escrito como\( u_t=k \Delta u \) o\( u_t=k \nabla^2 u \). Aquí los\( \nabla^2 \) símbolos\( \Delta \) y significan\( \dfrac{\partial^2}{\partial x^2}+ \dfrac{\partial^2}{\partial y^2}\). Vamos a utilizar\( \Delta\) a partir de ahora. La razón para usar tal notación es que se puede definir\( \Delta\) como lo correcto para cualquier número de dimensiones espaciales y luego la ecuación de calor es siempre\(u_t=k \Delta u\). El operador\( \Delta\) se llama el Laplaciano.
Bien, ahora que tenemos la notación fuera del camino, veamos cómo es una ecuación para la solución de estado estacionario. Estamos buscando una solución a la Ecuación de la\(\eqref{eq:3}\) que no dependa\(t\), o en otras palabras\(u_t=0\). De ahí que estemos buscando una función\(u(x,y)\) tal que
\[ \Delta u = u_{xx}+u_{yy}=0. \nonumber \]
Esta ecuación se llama la ecuación de Laplace \(^{1}\). Las soluciones a la ecuación de Laplace se denominan funciones armónicas y tienen muchas propiedades y aplicaciones agradables mucho más allá del problema de calor en estado estacionario.
Las funciones armónicas en dos variables ya no son solo lineales (gráficos planos). Por ejemplo, se puede comprobar que las funciones\(x^2-y^2\) y\(xy\) son armónicas. No obstante, si recuerdas tu cálculo multivariable observamos que si\(u_{xx}\) es positivo,\(u\) es cóncavo hacia arriba en la\(x\) dirección, entonces\(u_{yy}\) debe ser negativo y\(u\) debe ser cóncavo hacia abajo en la\(y\) dirección. Por lo tanto, una función armónica nunca puede tener ninguna “cima de colina” o “valle” en la gráfica. Esta observación es consistente con nuestra idea intuitiva de la distribución del calor en estado estacionario; el punto más caliente o frío no estará dentro.
Comúnmente, la ecuación de Laplace es parte de un llamado problema de Dirichlet \(^{2}\). Es decir, tenemos una región en el\(xy\) plano -y especificamos ciertos valores a lo largo de los límites de la región. Luego tratamos de encontrar una solución\(u\) definida en esta región tal que\(u\) concuerde con los valores que especificamos en el límite.
Por simplicidad, consideramos una región rectangular. También por simplicidad especificamos que los valores de límite sean cero en 3 de los cuatro bordes y solo especificamos una función arbitraria en un borde. Como todavía tenemos el principio de superposición, podemos usar esta solución más simple para derivar la solución general para valores de límite arbitrarios resolviendo 4 problemas diferentes, uno para cada borde, y sumando esas soluciones juntas. Esta configuración se deja como un ejercicio.
Deseamos resolver el siguiente problema. Dejar\(h\) y\(w\) ser la altura y anchura de nuestro rectángulo, con una esquina en el origen y acostado en el primer cuadrante.
\[\begin{align} & \Delta u = 0 , & & \label{dirich:eq1} \\ & u(0,y) = 0 & & \text{for } 0 < y < h,\label{dirich:eq2} \\ & u(x,h) = 0 & & \text{for } 0 < x < w,\label{dirich:eq3} \\ & u(w,y) = 0 & & \text{for } 0 < y < h,\label{dirich:eq4} \\ & u(x,0) = f(x) & & \text{for } 0 < x < w.\label{dirich:eq5}\end{align} \]
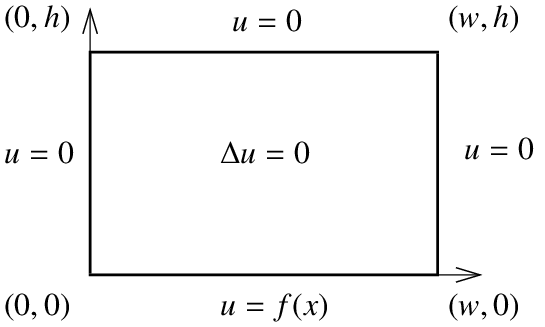
El método que aplicamos es la separación de variables. Nuevamente, encontraremos suficientes soluciones de bloques de construcción que satisfagan todas las condiciones de contorno homogéneas (todas las condiciones excepto\(\eqref{dirich:eq5}\)). Observamos que la superposición aún funciona para la ecuación y todas las condiciones homogéneas. Por lo tanto, podemos usar la serie de Fourier\(f(x)\) para resolver el problema como antes.
Lo intentamos\(u(x,y)=X(x)Y(y)\). Nos conectamos\(u\) a la ecuación para obtener
\[X''Y+XY''=0. \nonumber \]
Ponemos la\(X\) s de un lado y la\(Y\) s del otro para conseguir
\[ - \dfrac{X''}{X}= \dfrac{Y''}{Y}. \nonumber \]
El lado izquierdo solo depende de\(x\) y el lado derecho solo depende de\(y\). Por lo tanto, hay alguna constante\( \lambda \) tal que\( \lambda = \dfrac{-X''}{X}= \dfrac{Y''}{Y}\). Y obtenemos dos ecuaciones
\[ X'' + \lambda X = 0, \\ Y'' - \lambda Y=0. \nonumber \]
Además, las condiciones de límite homogéneas implican que\(X(0)=X(w)=0\) y\(Y(h)=0\). Tomando la ecuación porque ya\(X\) hemos visto que tenemos una solución no trivial si y solo si\( \lambda= \lambda_n = \dfrac{n^2 \pi^2}{w^2}\) y la solución es un múltiplo de
\[ X_n(x) = \sin \left( \dfrac{n \pi}{w}x \right). \nonumber \]
Para estos dados\( \lambda_n \), la solución general para\(Y\) (uno por cada\(n\)) es
\[\label{eq:14} Y_n(y)=A_n \cosh \left( \dfrac{n \pi}{w}y \right) + B_n \sinh \left( \dfrac{n \pi}{w}y \right). \]
Solo tenemos una condición\(Y_n\) y por lo tanto podemos elegir uno de\(A_n\) o\(B_n\) para ser algo conveniente. Será útil tener\(Y_n(0)=1\), así que dejamos\(A_n=1\). Configurando\(Y_n(h)=0\) y resolviendo para\(B_n\) que lo consigamos
\[ B_n = \dfrac{ - \cosh \left( \dfrac{n \pi h}{w} \right)}{ \sinh \left( \dfrac{n \pi h}{w} \right)}. \nonumber \]
Después de enchufarlo\(A_n\) y\(B_n\) lo simplificamos, encontramos\(\eqref{eq:14}\)
\[ Y_n(y) = \dfrac{ \sinh \left( \dfrac{n \pi (h-y)}{w} \right)}{ \sinh \left( \dfrac{n \pi h}{w} \right)}. \nonumber \]
Definimos\(u_n(x,y)=X_n(x)Y_n(y)\). Y tenga en cuenta que\(u_n\) satisface\(\eqref{dirich:eq1}\) -\(\eqref{dirich:eq4}\).
Observe que
\[ u_n(x,0)= X_n(x)Y_n(0) = \sin \left( \dfrac{n \pi}{w}x \right). \nonumber \]
Supongamos
\[ f(x)= \sum_{n=1}^{ \infty}b_n \sin \left( \dfrac{n \pi x}{w} \right). \nonumber \]
Entonces obtenemos una solución de\(\eqref{dirich:eq1}\) -\(\eqref{dirich:eq5}\) de la siguiente forma.
\[ u(x,y)= \sum_{n=1}^{ \infty}b_n u_n(x,y) = \sum_{n=1}^{ \infty}b_n \sin \left( \dfrac{n \pi }{w}x \right) \left( \dfrac{ \sinh \left( \dfrac{n \pi (h-y)}{w} \right)}{ \sinh \left( \dfrac{n \pi h}{w} \right)} \right). \nonumber \]
Como\(u_n\) satisface Ecuación\(\eqref{dirich:eq1}\)\(\eqref{dirich:eq4}\) -y cualquier combinación lineal (finita o infinita) de también\(u_n\) debe satisfacer\(\eqref{dirich:eq1}\) -\(\eqref{dirich:eq4}\), vemos que\(u\) debe satisfacer Ecuaciones\(\eqref{dirich:eq1}\) -\(\eqref{dirich:eq4}\). Al enchufar\(y=0\) es fácil ver que\(u\) satisface\(\eqref{dirich:eq5}\) también.
Supongamos que tomamos\(w=h= \pi\) y dejamos\(f(x)= \pi\). Calculamos la serie sinusoidal para la función\( \pi\) (obtendremos la onda cuadrada). Encontramos que para\(0<x< \pi\) nosotros tenemos
\[ f(x)= \sum_ {\underset{n~ {\rm{odd}} }{n=1}}^{ \infty} \dfrac{4}{n} \sin(n x). \nonumber \]
Por lo tanto\(u(x,y)\), la solución\(\PageIndex{2}\), ver Figura, al problema de Dirichlet correspondiente se da como
\[ u(x,y)= \sum_ {\underset{n~ {\rm{odd}} }{n=1}}^{ \infty} \dfrac{4}{n} \sin(n x) \left( \dfrac{ \sinh(n( \pi-y)) }{ \sinh(n \pi) } \right). \nonumber \]
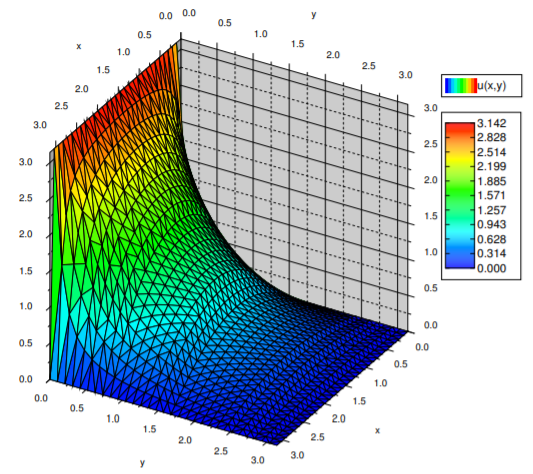
Este escenario corresponde a la temperatura de estado estacionario sobre una placa cuadrada de ancho\( \pi\) with 3 sides held at 0 degrees and one side held at \( \pi\) degrees. If we have arbitrary initial data on all sides, then we solve four problems, each using one piece of nonhomogeneous data. Then we use the principle of superposition to add up all four solutions to have a solution to the original problem.
Una forma diferente de visualizar soluciones de la ecuación de Laplace es tomar un cable y doblarlo para que corresponda a la gráfica de la temperatura por encima del límite de su región. Corte una lámina de goma en la forma de su región, un cuadrado en nuestro caso, y estírela fijando los bordes de la lámina al alambre. La lámina de caucho es una buena aproximación de la gráfica de la solución a la ecuación de Laplace con los datos de límite dados.


