5.3: Soluciones Periódicas Estables
- Page ID
- 115515
Cuerda Vibradora Forzada
Considera una cuerda de guitarra de longitud\(L\). Estudiamos esta configuración en la Sección 4.7. Dejar\(x\) ser la posición en la cuerda,\(t\) el tiempo, y\(y\) el desplazamiento de la cuerda. Ver Figura\(\PageIndex{1}\).
El problema se rige por las ecuaciones
\[\label{eq:1} \begin{array}{ll} y_{tt} = a^2 y_{xx} , & \\ y(0,t) = 0 , & y(L,t) = 0 , \\ y(x,0) = f(x) , & y_t(x,0) = g(x) . \end{array} \]
Vimos anteriormente que la solución es de la forma
\[ y= \sum_{n=1}^{\infty} \left( A_n\cos \left( \frac{n\pi a}{L}t \right) + B_n\sin \left( \frac{n\pi a}{L}t \right) \right) \sin \left( \frac{n\pi }{L}x \right), \nonumber \]
donde\(A_n\) y\(B_n\) fueron determinados por las condiciones iniciales. Las frecuencias naturales del sistema son las frecuencias (circulares)\(\frac{n\pi a}{L}\) para números enteros\(n \geq 1\).
Pero estas son vibraciones libres. Y si hay una fuerza externa que actúa sobre la cuerda. Supongamos que digamos vibraciones del aire (ruido), por ejemplo una segunda cuerda. O tal vez un motor a reacción. Por simplicidad, asume un sonido puro y agradable y asume que la fuerza es uniforme en cada posición de la cuerda. Digamos\(F(t)=F_0 \cos(\omega t)\) como fuerza por unidad de masa. Entonces nuestra ecuación de onda se convierte (recuerda que la fuerza es la masa por la aceleración)
\[\label{eq:3} y_{tt}=a^2y_{xx}+F_0\cos(\omega t), \]
con las mismas condiciones de límite, por supuesto.
Queremos encontrar aquí la solución que satisfaga la ecuación anterior y
\[\label{eq:4} y(0,t)=0,~~~~~y(L,t)=0,~~~~~y(x,0)=0,~~~~~y_t(x,0)=0. \]
Es decir, la cuerda está inicialmente en reposo. Primero encontramos una solución particular\(y_p\) de\(\eqref{eq:3}\) que satisfaga\(y(0,t)=y(L,t)=0\). Definimos las funciones\(f\) y\(g\) como
\[f(x)=-y_p(x,0),~~~~~g(x)=- \frac{\partial y_p}{\partial t}(x,0). \nonumber \]
Luego encontramos solución\(y_c\) de\(\eqref{eq:1}\). Si sumamos las dos soluciones, encontramos que\(y=y_c+y_p\) se resuelve\(\eqref{eq:3}\) con las condiciones iniciales.
Verifique que\(y=y_c+y_p\) resuelva\(\eqref{eq:3}\) y las condiciones laterales\(\eqref{eq:4}\).
Entonces, el gran problema aquí es encontrar la solución particular\(y_p\). Miramos la ecuación y hacemos una suposición educada
\[y_p(x,t)=X(x)\cos(\omega t). \nonumber \]
Nos enchufamos para obtener
\[ - \omega^2X\cos(\omega t)=a^2X''\cos(\omega t), \nonumber \]
o\(- \omega X=a^2X''+F_0\) después de cancelar el coseno. Sabemos encontrar una solución general a esta ecuación (es una ecuación de coeficiente constante no homogénea). La solución general es
\[ X(x)=A\cos \left( \frac{\omega}{a}x \right)+B\sin \left( \frac{\omega}{a}x \right)- \frac{F_0}{\omega^2}. \nonumber \]
Las condiciones de punto final implican\(X(0)=X(L)=0\). Entonces
\[ 0=X(0)=A- \frac{F_0}{\omega^2}, \nonumber \]
o\(A=\frac{F_0}{\omega^2}\), y también
\[ 0=X(L)= \frac{F_0}{\omega^2} \cos \left( \frac{\omega L}{a} \right)+B\sin \left( \frac{\omega L}{a} \right)- \frac{F_0}{\omega^2}. \nonumber \]
Asumiendo que no\(\sin \left( \frac{\omega L}{a} \right) \) es cero podemos resolver\(B\) para conseguir
\[\label{eq:11} B=\frac{-F_0 \left( \cos \left( \frac{\omega L}{a} \right)-1 \right)}{- \omega^2 \sin \left( \frac{\omega L}{a} \right)}. \]
Por lo tanto,
\[ X(x)= \frac{F_0}{\omega^2} \left( \cos \left( \frac{\omega}{a}x \right)- \frac{ \cos \left( \frac{\omega L}{a} \right)-1 }{ \sin \left( \frac{\omega L}{a} \right)}\sin \left( \frac{\omega}{a}x \right)-1 \right). \nonumber \]
La solución particular\(y_p\) que estamos buscando es
\[ y_p(x,t)= \frac{F_0}{\omega^2} \left( \cos \left( \frac{\omega}{a}x \right)- \frac{ \cos \left( \frac{\omega L}{a} \right)-1 }{ \sin \left( \frac{\omega L}{a} \right)}\sin \left( \frac{\omega}{a}x \right)-1 \right) \cos(\omega t). \nonumber \]
Verifica que\(y_p\) funcione.
Ahora llegamos al punto en que nos saltamos. Supongamos que\(\sin \left( \frac{\omega L}{a} \right)=0\). Lo que esto significa es que\(\omega\) es igual a una de las frecuencias naturales del sistema, es decir, un múltiplo de\( \frac{\pi a}{L}\). Notamos que si no\(\omega\) es igual a un múltiplo de la frecuencia base, sino que está muy cerca, entonces el coeficiente\(B\) in\(\eqref{eq:11}\) parece llegar a ser muy grande. Pero no saquemos conclusiones todavía. Cuando\(\omega = \frac{n\pi a}{L}\) para\(n\) par, entonces\(\cos \left( \frac{\omega L}{a} \right)=1\) y por lo tanto realmente lo conseguimos\(B=0\). Por lo que la resonancia se produce sólo cuando ambos\(\cos \left( \frac{\omega L}{a} \right)=-1\) y\(\sin \left( \frac{\omega L}{a} \right)=0\). Ahí es cuando\(\omega = \frac{n\pi a}{L}\) para impar\(n\).
Podríamos volver a resolver para la solución de resonancia si quisiéramos, pero es, en el sentido correcto, el límite de las soluciones a medida que\(\omega\) se acerca a una frecuencia de resonancia. En la vida real, la resonancia pura nunca ocurre de todos modos.
El cálculo anterior explica por qué una cadena comenzará a vibrar si la cuerda idéntica es arrancada cerca. En ausencia de fricción esta vibración se haría cada vez más fuerte con el paso del tiempo. Por otro lado, es poco probable que obtenga una gran vibración si la frecuencia de forzamiento no está cerca de una frecuencia de resonancia incluso si tiene un motor a reacción funcionando cerca de la cuerda. Es decir, la amplitud no seguirá aumentando a menos que sintonices solo la frecuencia correcta.
Fenómenos de resonancia similares ocurren cuando rompes una copa de vino usando voz humana (sí esto es posible, pero no es fácil \(^{1}\)) si le sucede que golpea la frecuencia justa. Recuerda que un vaso tiene un sonido mucho más puro, es decir, es más como un vibráfono, por lo que hay muchas menos frecuencias de resonancia para golpear.
Cuando la función de forzamiento es más complicada, la descompones en términos de la serie de Fourier y se aplica el resultado anterior. También puede necesitar resolver el problema anterior si la función de forzamiento es un seno en lugar de un coseno, pero si lo piensa, la solución es casi la misma.
Hagamos el cálculo para valores específicos. Supongamos\(F_0=1\)\(\omega =1\) y\(L=1\) y y\(a=1\). Entonces
\[ y_p(x,t)= \left( \cos(x)- \frac{ \cos(1)-1 }{ \sin(1)}\sin(x)-1 \right) \cos(t). \nonumber \]
Escribe\(B= \frac{ \cos(1)-1 }{ \sin(1)} \) para simplificar.
Luego, conéctelo\(t=0\) para obtener
\[f(x)=-y_p(x,0)=- \cos x+B \sin x+1, \nonumber \]
y después de diferenciar en\( t\) vemos eso\(g(x)=- \frac{\partial y_P}{\partial t}(x,0)=0\).
De ahí que para encontrar\(y_c\) necesitamos resolver el problema
\[\begin{align}\begin{aligned} & y_{tt} = y_{xx} , \\ & y(0,t) = 0 , \quad y(1,t) = 0 , \\ & y(x,0) = - \cos x + B \sin x +1 , \\ & y_t(x,0) = 0 .\end{aligned}\end{align} \nonumber \]
Tenga en cuenta que la fórmula que usamos para definir no\(y(x,0)\) es extraña, de ahí que no sea una simple cuestión de enchufar para aplicar la fórmula D'Alembert directamente! Debe definir\(F\) que es la extensión impar, 2-periódica de\(y(x,0)\). Entonces nuestra solución se vería como
\[\label{eq:17} y(x,t)= \frac{F(x+t)+F(x-t)}{2}+ \left( \cos(x) - \frac{\cos(1)-1}{\sin(1)}\sin(x)-1 \right) \cos(t). \]
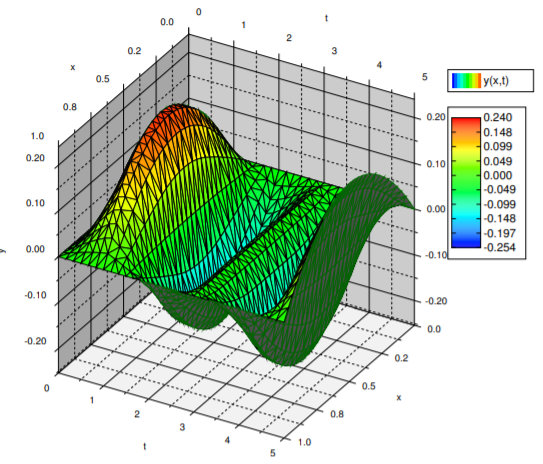
No es difícil calcular valores específicos para una extensión impar de una función y, por lo tanto,\(\eqref{eq:17}\) es una solución maravillosa al problema. Por ejemplo es muy fácil que una computadora lo haga, a diferencia de una solución en serie. Se da una gráfica en la Figura\(\PageIndex{2}\).
Oscilaciones de temperatura subterránea
Dejar\(u(x,t)\) ser la temperatura en un lugar determinado a profundidad\(x\) bajo tierra en el momento\(t\). Ver Figura\(\PageIndex{3}\).
La temperatura\(u\) satisface la ecuación de calor\(u_t=ku_{xx}\), donde\(k\) está la difusividad del suelo. Conocemos la temperatura en la superficie a\(u(0,t)\) partir de los registros meteorológicos. Supongamos por simplicidad que
\[ u(0,t)=T_0+A_0 \cos(\omega t), \nonumber \]
donde\(T_0\) esta la temperatura media anual, y\(t=0\) es pleno verano (puedes poner signo negativo arriba para que sea pleno invierno si lo deseas). \(A_0\)da la variación típica para el año. Es decir, la temperatura más calurosa es\(T_0+A_0\) y la más fría es\(T_0-A_0\). Por simplicidad, vamos a asumir eso\(T_0=0\). La frecuencia\(\omega\) se escoge dependiendo de las unidades de\(t\), de tal manera que cuando\(t=1\), entonces\(\omega t=2\pi\). Por ejemplo si\(t\) es en años, entonces\(\omega=2\pi\).
Parece razonable que la temperatura a profundidad también\(x\) oscile con la misma frecuencia. Esta, de hecho, será la solución periódica constante, independiente de las condiciones iniciales. Así que estamos buscando una solución de la forma
\[ u(x,t)=V(x)\cos(\omega t)+ W(x)\sin(\omega t). \nonumber \]
para el problema
\[\label{eq:20} u_t=ku_{xx,}~~~~~~u(0,t)=A_0\cos(\omega t). \]
Emplearemos lo exponencial complejo aquí para simplificar los cálculos. Supongamos que tenemos una función valorada compleja
\[h(x,t)=X(x)e^{i \omega t}. \nonumber \]
Vamos a buscar un\(h\) tal que\({\rm Re} h=u\). Para encontrar una\(h\), cuya parte real satisface\(\eqref{eq:20}\), buscamos una\(h\) tal que
\[\label{eq:22} h_t=kh_{xx,}~~~~~~h(0,t)=A_0 e^{i \omega t}. \]
Supongamos\(h\) que satisface\(\eqref{eq:22}\). Usa la fórmula de Euler para el exponencial complejo para verificar que\(u={\rm Re}\: h\) satisface\(\eqref{eq:20}\).
Sustituir\(h\) en\(\eqref{eq:22}\).
\[ i \omega Xe^{i \omega t}=kX''e^{i \omega t}. \nonumber \]
Por lo tanto,
\[ kX''-i \omega X=0, \nonumber \]
o
\[ X''- \alpha^2 X=0, \nonumber \]
donde\( \alpha = \pm \sqrt{\frac{i \omega }{k}}\). Tenga en cuenta\(\pm \sqrt{i}= \pm \frac{1=i}{\sqrt{2}}\) que para que pueda simplificar a\( \alpha= \pm (1+i) \sqrt{\frac{\omega}{2k}}\). De ahí que la solución general sea
\[ X(x)=Ae^{-(1+i)\sqrt{\frac{\omega}{2k}x}}+Be^{(1+i)\sqrt{\frac{\omega}{2k}x}}. \nonumber \]
Asumimos que un\(X(x)\) que solucione el problema debe estar acotado como\(x \rightarrow \infty\) ya\(u(x,t)\) debe estar acotado (¡no nos preocupamos por el núcleo de la tierra!). Si usas la fórmula de Euler para expandir los exponenciales complejos, notarás que el segundo término estará sin límites (si\(B \neq 0\)), mientras que el primer término siempre está acotado. De ahí\(B=0\).
Usa la fórmula de Euler para mostrar\(e^{(1+i)\sqrt{\frac{\omega}{2k}x}}\) que no tiene límites como\(x \rightarrow \infty\), mientras que\(e^{-(1+i)\sqrt{\frac{\omega}{2k}x}}\) está acotado como\(x \rightarrow \infty\).
Además,\(X(0)=A_0\) ya que\(h(0,t)=A_0e^{i \omega t}\). Por lo tanto\(A=A_0\). Esto significa que
\[ h(x,t)=A_0e^{-(1+i)\sqrt{\frac{\omega}{2k}x}}e^{i \omega t}=A_0e^{-(1+i)\sqrt{\frac{\omega}{2k}}x+i \omega t}=A_0e^{- \sqrt{\frac{\omega}{2k}}x}e^{i( \omega t- \sqrt{\frac{\omega}{2k}}x)}. \nonumber \]
Tendremos que obtener la parte real de\(h\), así que aplicamos la fórmula de Euler para obtener
\[ h(x,t)=A_0e^{- \sqrt{\frac{\omega}{2k}}x} \left( \cos \left( \omega t - \sqrt{\frac{\omega}{2k}x} \right) +i \sin \left( \omega t - \sqrt{\frac{\omega}{2k}x} \right) \right). \nonumber \]
Entonces finalmente
\[u(x,t)={\rm Re}h(x,t)=A_0e^{- \sqrt{\frac{\omega}{2k}}x} \cos \left( \omega t- \sqrt{\frac{\omega}{2k}}x \right). \nonumber \]
¡Yay!
Observe que la fase es diferente a diferentes profundidades. A profundidad la fase se retrasa por\(x \sqrt{\frac{\omega}{2k}}\). Por ejemplo en unidades cgs (centímetros-gramos-segundos) tenemos\(k=0.005\) (valor típico para suelo),\(\omega = \frac{2\pi}{\text{seconds in a year}}=\frac{2\pi}{31,557,341}\approx 1.99\times 10^{-7}\). Entonces si calculamos donde el desplazamiento de fase\(x\sqrt{\frac{\omega}{2k}}=\pi\) encontramos la profundidad en centímetros donde se invierten las estaciones. Es decir, obtenemos la profundidad a la que el verano es el más frío y el invierno es el más cálido. Obtenemos aproximadamente\(700\) centímetros, que es aproximadamente\(23\) pies bajo tierra.
Tenga cuidado de no sacar conclusiones. Los cambios de temperatura se descomponen rápidamente a medida que profundiza. La amplitud de los cambios de temperatura es\(A_0e^{- \sqrt{\frac{\omega}{2k}}x}\). Esta función decae muy rápidamente a medida que\(x\) (la profundidad) crece. Tomemos de nuevo parámetros típicos como los anteriores. También asumiremos que nuestra oscilación de temperatura superficial es\(\pm 15^{\circ}\) Celsius, es decir,\(A_0=15\). Entonces la variación máxima de temperatura a\(700\) centímetros es de sólo\(\pm 0.66^{\circ}\) Celsius.
No es necesario cavar muy profundo para obtener un “refrigerador” efectivo, con temperatura casi constante. Es por ello que los vinos se guardan en una bodega; se necesita temperatura constante. El diferencial de temperatura también podría ser utilizado para la energía. Un hogar podría calentarse o enfriarse aprovechando el hecho anterior. Incluso sin el núcleo de tierra podrías calentar una casa en invierno y enfriarla en verano. El núcleo de tierra hace que la temperatura sea más alta cuanto más profundo cavas, aunque necesitas cavar algo profundo para sentir la diferencia. Eso no lo tomamos en cuenta anteriormente.
Notas al pie
[1] Cazadores de mitos, episodio 31, Discovery Channel, originalmente emitido el 18 de mayo de 2005.


