6.2: Transformadas de derivados y ODEs
- Page ID
- 115284
Transformas de derivados
Veamos cómo se utiliza la transformada de Laplace para las ecuaciones diferenciales. Primero intentemos encontrar la transformación de Laplace de una función que sea derivada. Supongamos que\(g(t)\) es una función diferenciable de orden exponencial, es decir,\(|g(t)| \leq Me^{ct}\) para algunos\(M\) y\(c\). Así\(\mathcal{L}\{g(t)\}\) existe, y lo que es más,\(\lim_{t \rightarrow \infty}e^{-st}g(t)=0\) cuándo\(s>c\). Entonces
\[ \mathcal{L}\{g'(t)\}= \int_0^{\infty}e^{-st}g'(t)dt= \left[ e^{-st}g(t) \right]_{t=0}^{\infty}- \int_0^{\infty}(-s)e^{-st}g(t)dt=-g(0)+s \mathcal{L}\{g(t)\}. \nonumber \]
Repetimos este procedimiento para derivados superiores. Los resultados se listan en la Tabla\(\PageIndex{1}\). El procedimiento también funciona para funciones lisas por partes, es decir, funciones que son continuas por tramos con una derivada continua por tramos. El hecho de que la función sea de orden exponencial se utiliza para mostrar que existen los límites que aparecen arriba. No vamos a preocuparnos mucho por este hecho.
| \(f(t)\) | \(\mathcal{L}\{f(t)\}=F(s)\) |
|---|---|
| \ (f (t)\) ">\(g'(t)\) | \ (\ mathcal {L}\ {f (t)\} =F (s)\) ">\(sG(s)-g(0)\) |
| \ (f (t)\) ">\(g''(t)\) | \ (\ mathcal {L}\ {f (t)\} =F (s)\) ">\(s^2G(s)-sg(0)-g'(0)\) |
| \ (f (t)\) ">\(g'''(t)\) | \ (\ mathcal {L}\ {f (t)\} =F (s)\) ">\(s^3G(s)-s^2g(0)-sg'(0)-g''(0)\) |
Resolviendo ODEs con la Transformación de Laplace
Observe que la transformación de Laplace convierte la diferenciación en multiplicación por\(s\). Veamos cómo aplicar este hecho a las ecuaciones diferenciales.
Toma la ecuación
\[ x''(t) + x(t) = \cos (2t),~~~~~~~ x(0)=0, ~~~~~~~ x'(0)=1. \nonumber \]
Tomaremos la transformación de Laplace de ambos lados. Por\(X(s)\) vamos a, como de costumbre, denotar la transformación de Laplace de\(x(t)\).
\[\begin{align}\begin{aligned} \mathcal{L}\{x''(t)+x(t)\} &= \mathcal{L}\{\cos(2t)\}, \\ s^2X(x)-sx(0)+x'(0)+X(s)&= \frac{s}{s^2+4}.\end{aligned}\end{align} \nonumber \]
Conectamos las condiciones iniciales ahora, esto hace que los cálculos sean más optimizados, para obtener
\[s^2X(s) - 1 + X(s) = \dfrac{s}{s^2+4}. \nonumber \]
Resolvemos para\(X(s)\),
\[X(s) = \dfrac{s}{(s^2+1)(s^2+4)} + \dfrac{1}{s^2+1}. \nonumber \]
Usamos fracciones parciales (ejercicio) para escribir
\[ X(s) = \dfrac{1}{3}\dfrac{s}{s^2+1}-\dfrac{1}{3}\dfrac{s}{s^2+4} + \dfrac{1}{s^2+1}. \nonumber \]
Ahora toma la transformada inversa de Laplace para obtener
\[ x(t) = \dfrac{1}{3}\cos (t) - \dfrac{1}{3} \cos (2t) + \sin (t). \nonumber \]
El procedimiento para las ecuaciones de coeficiente constante lineal es el siguiente. Tomamos una ecuación diferencial ordinaria en la variable de tiempo\(t\). Aplicamos la transformada de Laplace para transformar la ecuación en una ecuación algebraica (no diferencial) en el dominio de la frecuencia. Todos los\(x(t)\),\(x'(t)\),\(x''(t)\), y así sucesivamente, se convertirán en\(X(s)\),\(sX(s)-x(0)\),\(s^2X(s) - sx(0) - x'(0)\), y así sucesivamente. Resolvemos la ecuación para\(X(s)\). Entonces tomando la transformada inversa, si es posible, nos encontramos\(x(t)\).
Cabe señalar que dado que no todas las funciones tienen una transformada de Laplace, no todas las ecuaciones pueden resolverse de esta manera. Además, si la ecuación no es un coeficiente constante lineal ODE, entonces aplicando la transformada de Laplace es posible que no obtengamos una ecuación algebraica.
Uso de la función Heaviside
Antes de pasar a ecuaciones más generales que las que podríamos resolver antes, queremos considerar la función Heaviside. Ver Figura\(\PageIndex{1}\) para la gráfica.
\[u(t)=\left\{ \begin{array}{cc} 0 & {\rm{if~}}t<0, \\ 1 & {\rm{if~}}t \geq 0. \end{array} \right. \nonumber \]
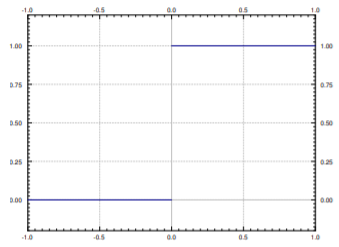
Esta función es útil para armar funciones o cortar funciones. Más comúnmente se usa como\(u(t-a)\) para alguna constante\(a\). Esto simplemente desplaza la gráfica hacia la derecha por\(a\). Es decir, es una función que es 0 cuando\(<a\) y 1 cuando\(t \ge a\). Supongamos por ejemplo que\(f(t)\) es una “señal” y empezaste a recibir la señal\(\sin t\) en el momento\( t = \pi\). La función\(f(t)\) debería definirse como
\[f(t)=\left\{ \begin{array}{cc} 0 & {\rm{if~}}t< \pi , \\ \sin t & {\rm{if~}}t \geq \pi . \end{array} \right. \nonumber \]
Usando la función Heaviside, se\(f(t)\) puede escribir como
\[ f(t) = u(t- \pi) \sin t \nonumber \]
Del mismo modo, la función de paso que está\(1\) en el intervalo\( [1,2)\) y cero en todas partes se puede escribir como
\[ u(t-1) - u(t-2). \nonumber \]
La función Heaviside es útil para definir funciones definidas por partes. Si quieres definir\(f(t)\) tal que\(f(t)=t\) cuando\(t\) está en\([0,1]\),\(f(t) = -t +2\) cuando\(t\) está en\([1,2)\) y de\(f(t)=0\) otra manera, puedes usar la expresión
\[ f(t) = t \left(u(t) -u(t-1)\right) + (-t+2) \left(u(t-1)-u(t-2) \right). \nonumber \]
De ahí que sea útil conocer cómo interactúa la función Heaviside con la transformación de Laplace. Ya hemos visto que
\[ \mathcal{L} \{ u(t-a)\} = \dfrac{e^{-as}}{2}. \nonumber \]
Propiedad Shifting
Esto puede generalizarse en una propiedad de desplazamiento o una segunda propiedad de desplazamiento.
\[\label{eq:14} \mathcal{L} \{ f(t-a)u(t-a) \} = e^{-as} \mathcal{L} \{ f(t) \}. \]
Supongamos que la función de forzamiento no es periódica. Por ejemplo, supongamos que teníamos un sistema masa-resorte
\[ x''(t) + x(t) = f(t), ~~~~~~ x(0) = 0,~~~~~~ x'(0) = 0, \nonumber \]
donde\(f(t)=1\) si\(1 \le t < 5\) y cero de otra manera. Podríamos imaginar un sistema de muelles masivos, donde se dispara un cohete durante 4 segundos a partir de las\(t=1\). O tal vez un circuito RLC, donde el voltaje se eleva a una velocidad constante durante 4 segundos comenzando en\(t=1\), y luego se mantiene estable nuevamente comenzando en\(t=5\).
Podemos escribir\(f(t) = u(t-1) - u(t-5)\). Transformamos la ecuación y enchufamos las condiciones iniciales como antes para obtener
\[ s^2X(s) + X(s) = \dfrac{e^{-s}}{s}-\dfrac{e^{-5s}}{s}. \nonumber \]
Resolvemos\(X(s)\) para obtener
\[ X(s) = \dfrac{e^{-s}}{s(s^2+1)} - \dfrac{e^{-5s}}{s(s^2+1)}. \nonumber \]
Lo dejamos como ejercicio al lector para demostrar que
\[ \mathcal{L}^{-1} \left\{ \dfrac{1}{s(s^2+1)} \right\} =1 - \cos t. \nonumber \]
En otras palabras\(\mathcal{L}\{1-\cos t \} = \frac{1}{s(s^2+1)}\). Entonces usando\(\eqref{eq:14}\) encontramos
\[ \mathcal{L}^{-1}\left\{\frac{e^{-s}}{s(s^2+1)}\right\}=\mathcal{L}^{-1}\{e^{-s}\mathcal{L}\{1-\cos t \} \}=(1-\cos(t-1))u(t-1). \nonumber \]
Del mismo modo
\[ \mathcal{L}^{-1}\left\{\frac{e^{-5s}}{s(s^2+1)}\right\}=\mathcal{L}^{-1}\{e^{-5s}\mathcal{L}\{1-\cos t \} \}=(1-\cos(t-5))u(t-5). \nonumber \]
Por lo tanto, la solución es
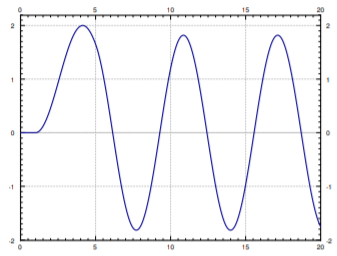
\[ x(t) = \left( 1 - \cos (t-1) \right) u(t-1) - \left(1-\cos (t-5) \right) u(t-5). \nonumber \]
La gráfica de esta solución se da en la Figura\(\PageIndex{2}\).
Funciones de transferencia
La transformación de Laplace lleva al siguiente concepto útil para estudiar el comportamiento en estado estacionario de un sistema lineal. Supongamos que tenemos una ecuación de la forma
\[ Lx = f(t), \nonumber \]
donde\(L\) es un operador diferencial de coeficiente constante lineal. Entonces generalmente\(f(t)\) se piensa como entrada del sistema y\(x(t)\) se piensa como la salida del sistema. Por ejemplo, para un sistema masa-resorte la entrada es la función de forzamiento y la salida es el comportamiento de la masa. Nos gustaría tener una manera conveniente de estudiar el comportamiento del sistema para diferentes entradas.
Supongamos que todas las condiciones iniciales son cero y tomamos la transformada de Laplace de la ecuación, obtenemos la ecuación
\[ A(s)X(s) = F(s). \nonumber \]
Resolviendo para la relación\(\frac{X(s)}{F(s)}\) obtenemos la llamada función de transferencia\(H(s)=\frac{1}{A(s)}\).
\[ H(s) = \dfrac{X(s)}{F(s)} \nonumber \]
En otras palabras,\(X(s) = H(s)F(s)\). Obtenemos una dependencia algebraica de la salida del sistema basada en la entrada. Ahora podemos estudiar fácilmente el comportamiento de estado estacionario del sistema dado diferentes entradas simplemente multiplicando por la función de transferencia.
Dado\(x''+ \omega_0^2x=f(t)\), vamos a encontrar la función de transferencia (asumiendo que las condiciones iniciales son cero).
Primero, tomamos la transformación de Laplace de la ecuación.
\[ s^2X(s)+\omega_0^2X(s)=F(s). \nonumber \]
Ahora resolvemos para la función de transferencia\(\frac{X(s)}{F(s)}\).
\[H(s)= \frac{X(s)}{F(s)}= \frac{1}{s^2+ \omega_0^2}. \nonumber \]
Veamos cómo usar la función de transferencia. Supongamos que tenemos la entrada constante\(f(t)=1\). Por lo tanto\(F(s)=\frac{1}{s}\), y
\[X(s)= H(s)F(s)= \frac{1}{s^2+ \omega_0^2}\frac{1}{s}. \nonumber \]
Tomando la transformada inversa de Laplace de\(X(s)\) obtenemos
\[x(t)=\frac{1-\cos(\omega_0 t)}{ \omega_0^2}. \nonumber \]
Transformas de Integrales
Una característica de las transformaciones de Laplace es que también es capaz de lidiar fácilmente con ecuaciones integrales. Es decir, ecuaciones en las que aparecen integrales más que derivadas de funciones. La propiedad básica, que puede probarse aplicando la definición y haciendo integración por partes, es
\[ \mathcal{L} \left\{ \int_0^t f(\tau) \, d\tau \right\} = \dfrac{1}{s}F(s). \nonumber \]
A veces es útil (por ejemplo, para calcular la transformación inversa) escribir esto como
\[ \int_0^t f(\tau) \, d\tau = \mathcal{L}^{-1} \left\{\dfrac{1}{s}F(s)\right\}. \nonumber \]
Para computar\( \mathcal{L}^{-1} \left\{\dfrac{1}{s(s^2+1)}\right\} \) podríamos proceder aplicando esta regla de integración.
\[ \mathcal{L}^{-1} \left\{ \dfrac{1}{2} \dfrac{1}{s^2+1} \right\} = \int_0^t \mathcal{L}^{-1} \left \{ \dfrac{1}{s^2+1} \right\} = \int_0^t \sin \tau \, d\tau = 1 -\cos t. \nonumber \]
Una ecuación que contiene una integral de la función desconocida se denomina ecuación integral. Por ejemplo, tome
\[ t^2 = \int _0^t e^{\tau}x(\tau)\, d\tau \nonumber \]
donde deseamos resolver para\(x(t)\). Aplicamos la transformación de Laplace y la propiedad cambiante para obtener
\[ \dfrac{2}{s^3} = \dfrac{1}{s} \mathcal{L} \{ e^tx(t)\} = \dfrac{1}{s}X(s-1), \nonumber \]
donde\(X(s) = \mathcal{L} \{x(t) \}\). Así
\[ X(s-1) = \dfrac{2}{s^2}\quad\text{or}\quad X(s) = \dfrac{2}{(s+1)^2}. \nonumber \]
Utilizamos la propiedad de cambio de nuevo para obtener
\[ x(t) = 2e^{-t}t. \nonumber \]


