7.1: Serie Power

Muchas funciones se pueden escribir en términos de una serie de potencia

\[ \sum _{k=0}^{\infty} a_k(x-x_0)^k \nonumber \]

Si asumimos que una solución de una ecuación diferencial se escribe como una serie de potencias, entonces quizás podamos usar un método que recuerde a coeficientes indeterminados. Es decir, vamos a tratar de resolver por los números\(a_k\). Antes de que podamos llevar a cabo este proceso, revisemos algunos resultados y conceptos sobre series de potencia.

Definición

Como decíamos, una serie de poder es una expresión como

\[\label{eq:2} \sum_{k=0}^\infty a_k {(x-x_0)}^k =a_0 + a_1 (x-x_0) +a_2 {(x-x_0)}^2 +a_3 {(x-x_0)}^3 + \cdots , \]

donde\( a_0,a_1,a_2,\ldots,a_k,\ldots\) y\(x_0\) son constantes. Let

\[ S_n(x) = \sum_{k=0}^n a_k {(x-x_0)}^k =a_0 + a_1 (x-x_0) + a_2 {(x-x_0)}^2 + a_3 {(x-x_0)}^3 + \cdots + a_n {(x-x_0)}^n , \nonumber \]

denotan la llamada suma parcial. Si para algunos\(x\), el límite

\[ \lim_{n\to \infty} S_n(x) = \lim_{n\to\infty} \sum_{k=0}^n a_k {(x-x_0)}^k \nonumber \]

existe, entonces decimos que la serie\(\eqref{eq:2}\) converge en\(x\). Tenga en cuenta que para\(x=x_0\), la serie siempre converge a\(a_0\). Cuando\(\eqref{eq:2}\) converge en cualquier otro punto\(x \neq x_0\), decimos que\(\eqref{eq:2}\) es una serie de poder convergente. En este caso escribimos

\[ \sum_{k=0}^\infty a_k {(x-x_0)}^k = \lim_{n\to\infty} \sum_{k=0}^n a_k {(x-x_0)}^k. \nonumber \]

Si la serie no converge por ningún punto\(x \neq x_0\), decimos que la serie es divergente.

Ejemplo\(\PageIndex{1}\)

La serie

\[ \sum_{k=0}^\infty \frac{1}{k!} x^k = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \cdots \nonumber \]

es convergente para cualquier\(x\). Recordemos que\(k! = 1\cdot 2\cdot 3 \cdots k\) es lo factorial. Por convención definimos\(0!=1\). De hecho, tal vez recuerde que esta serie converge a\(e^x\).

Decimos que\(\eqref{eq:2}\) converge absolutamente en\(x\) cada vez que el límite

\[ \lim_{n\to\infty} \sum_{k=0}^n \lvert a_k \rvert \, {\lvert x-x_0 \rvert}^k \nonumber \]

existe. Es decir, la serie\(\sum_{k=0}^\infty \lvert a_k \rvert \, {\lvert x-x_0 \rvert}^k\) es convergente. Si\(\eqref{eq:2}\) converge absolutamente en\(x\), entonces converge en\(x\). Sin embargo, la implicación opuesta no es cierta.

Ejemplo\(\PageIndex{2}\)

La serie

\[\sum_{k=1}^\infty \frac{1}{k} \nonumber \]

converge absolutamente para todos\(x\) in the interval \((-1,1)\).

Converge en\(x=-1\), as

\(\sum_{k=1}^\infty \frac{{(-1)}^k}{k}\) converges (conditionally)

por la prueba en serie alterna.

Pero la serie power no converge absolutamente en\(x=-1\), because \(\sum_{k=1}^\infty \frac{1}{k}\) does not converge. The series diverges at \(x=1\).

Radio de Convergencia

Si una serie de potencias converge absolutamente en algunos\(x_1\), entonces para todos\(x\) tales que\(\lvert x - x_0 \rvert \leq \lvert x_1 - x_0 \vert\) (es decir,\(x\) está más cerca que\(x_1\) a\(x_0\)) tenemos\(\bigl\lvert a_k {(x-x_0)}^k \bigr\rvert \leq \bigl\lvert a_k {(x_1-x_0)}^k \bigr\rvert\) para todos\(k\). Como los números\(\bigl\lvert a_k {(x_1-x_0)}^k \bigr\rvert\) suman algún límite finito, sumar números positivos más pequeños también\(\bigl\lvert a_k {(x-x_0)}^k \bigr\rvert\) debe tener un límite finito. De ahí que la serie deba converger absolutamente en\(x\).

Teorema\(\PageIndex{1}\)

Para una serie de\(\eqref{eq:2}\) potencias, existe un número\(\rho\) (permitimos\(\rho =\infty \)) llamado el radio de convergencia tal que la serie converge absolutamente en el intervalo\((x_{0}-\rho ,\:x_{0}+\rho )\) y diverge para\(x<x_{0}-\rho \) y\(x>x_{0}+\rho \). Escribimos\(\rho =\infty \) si la serie converge para todos\(x\).

Figura\(\PageIndex{1}\): Convergencia de una serie de potencias.

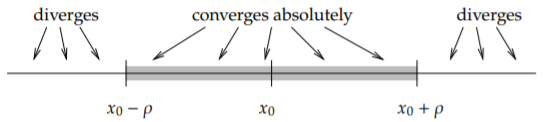
Ver Figura\(\PageIndex{1}\). En Ejemplo\(\PageIndex{1}\) el radio de convergencia es\(\rho = \infty\) as the series converges everywhere. In Example \(\PageIndex{2}\) el radio de convergencia es\(\rho=1\). We note that \(\rho = 0\) is another way of saying that the series is divergent. A useful test for convergence of a series is the ratio test. Suppose that

\[\sum_{k=0}^\infty c_k \nonumber \]

es una serie tal que el límite

\[L = \lim_{n\to\infty} \left \lvert \frac{c_{k+1}}{c_k} \right \rvert \nonumber \]

existe. Entonces la serie converge absolutamente si\(L < 1\) and diverges if \(L > 1\).

Apliquemos esta prueba a la serie\(\eqref{eq:2}\). Eso es que dejamos\(c_k = a_k {(x - x_0)}^k\) in the test. Compute

\[ L = \lim_{n\to\infty} \left \lvert \frac{c_{k+1}}{c_k} \right \rvert = \lim_{n\to\infty} \left \lvert \frac{a_{k+1} {(x - x_0)}^{k+1}}{a_k {(x - x_0)}^k} \right \rvert = \lim_{n\to\infty} \left \lvert\frac{a_{k+1}}{a_k}\right \rvert \lvert x - x_0 \rvert . \nonumber \]

Definir\(A\) by

\[A =\lim_{n\to\infty} \left \lvert \frac{a_{k+1}}{a_k} \right \rvert . \nonumber \]

Entonces si\(1 > L = A \lvert x - x_0 \rvert\) the series \(\eqref{eq:2}\) converge absolutamente. Si\(A = 0\), then the series always converges. If \(A > 0\), then the series converges absolutely if \(\lvert x - x_0 \rvert < \frac{1}{A}\), and diverges if \(\lvert x - x_0 \rvert > \frac{1}{A}\). That is, the radius of convergence is \(\frac{1}{A}\).

Una prueba similar es la prueba de raíz. Supongamos

\[L=\lim_{k\to\infty} \sqrt[3]{|c_{k}|} \nonumber \]

existe. Entonces\(\sum_{k=0}^{\infty}c_{k}\) converge absolutamente si\(L<1\) y diverge si\(L>1\). Podemos usar el mismo cálculo que el anterior para encontrar\(A\). Resumimos.

Teorema\(\PageIndex{2}\): Ratio and Root Tests for Power Series

Let

\[\sum_{k=0}^\infty a_k {(x-x_0)}^k \nonumber \]

ser una serie de potencia tal que

\[A = \lim_{n\to\infty} \left \lvert \frac{a_{k+1}}{a_k} \right \rvert\quad\text{or}\quad A=\lim_{k\to\infty}\sqrt[3]{|a_{k}|} \nonumber \]

existe. Si\(A = 0\), then the radius of convergence of the series is \(\infty\). Otherwise the radius of convergence is \(\frac{1}{A}\).

Ejemplo\(\PageIndex{3}\)

Supongamos que tenemos la serie

\[\sum_{k=0}^\infty 2^{-k} {(x-1)}^k . \nonumber \]

Primero calculamos,

\[A = \lim_{k\to\infty} \left \lvert \frac{a_{k+1}}{a_k} \right \rvert = \lim_{k\to\infty} \left \lvert \frac{2^{-k-1}}{2^{-k}} \right \rvert = 2^{-1} = \frac{1}{2}. \nonumber \]

Por lo tanto el radio de convergencia es\(2\), and the series converges absolutely on the interval \((-1,3)\). Y bien podríamos haber utilizado la prueba raíz:

\[A = \lim_{k\to\infty} \lim_{k\to\infty} \sqrt[k]{\lvert a_k \rvert} = \lim_{k\to\infty} \sqrt[k]{\lvert 2^{-k} \rvert} = \lim_{k\to\infty} 2^{-1} = \frac{1}{2}. \nonumber \]

Ejemplo\(\PageIndex{4}\)

Considera\[\sum_{k=0}^\infty \frac{1}{k^k} {x}^k . \nonumber \] Calcular el límite para la prueba raíz,\[A = \lim_{k\to\infty} \sqrt[k]{\lvert a_k \rvert} = \lim_{k\to\infty} \sqrt[k]{ \left\lvert\frac{1}{k^k}\right\rvert} = \lim_{k\to\infty} \sqrt[k]{ {\left\lvert\frac{1}{k}\right\rvert}^{k}} = \lim_{k\to\infty} \frac{1}{k} = 0 . \nonumber \] Entonces el radio de convergencia es\(\infty\): la serie converge en todas partes. La prueba de ratio también funcionaría aquí.

No siempre se aplica la prueba de raíz o relación. Ese es el límite de\(\bigl \lvert \frac{a_{k+1}}{a_k} \bigr \rvert\) o\(\sqrt[k]{\lvert a_k \rvert}\) podría no existir. Existen formas más sofisticadas de encontrar el radio de convergencia, pero esas estarían más allá del alcance de este capítulo. Los dos métodos anteriores cubren muchas de las series que surgen en la práctica. A menudo, si se aplica la prueba raíz, también lo hace la prueba de relación, y viceversa, aunque el límite podría ser más fácil de calcular de una manera que de otra.

Funciones analíticas

Las funciones representadas por series de potencia se denominan funciones analíticas. No todas las funciones son analíticas, aunque la mayoría de las funciones que has visto en el cálculo son. Una función analítica\(f(x)\) is equal to its Taylor series\(^{1}\) near a point \(x_0\). That is, for \(x\) near \(x_0\) we have

\[\label{eq:21} f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(x_0)}{k!} {(x-x_0)}^k , \]

donde\(f^{(k)}(x_0)\) denotes the \(k^{\text{th}}\) derivative of \(f(x)\) at the point \(x_0\).

Figura\(\PageIndex{2}\): La función sinusoidal y sus aproximaciones de Taylor alrededor\(x_o=0\) de y grado.

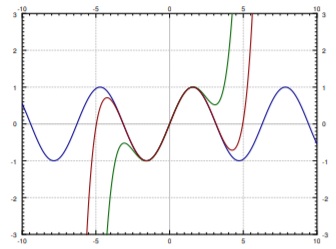
Por ejemplo, el seno es una función analítica y su serie Taylor\(x_0 = 0\) is given by

\[ \sin(x) = \sum_{n=0}^\infty \frac{{(-1)}^n}{(2n+1)!} x^{2n+1} . \nonumber \]

En la Figura\(\PageIndex{2}\) we plot \(\sin(x)\) and the truncations of the series up to degree 5 and 9. You can see that the approximation is very good for \(x\) near 0, but gets worse for \(x\) further away from 0. This is what happens in general. To get a good approximation far away from \(x_0\) you need to take more and more terms of the Taylor series.

Manipulación de la serie Power

Una de las principales propiedades de las series de poder que vamos a utilizar es que podemos diferenciarlas término por término. Es decir, supongamos que\(\sum a_k {(x-x_0)}^k\) is a convergent power series. Then for \(x\) in the radius of convergence we have

\[\frac{d}{dx} \left[\sum_{k=0}^\infty a_k {(x-x_0)}^k\right]=\sum_{k=1}^\infty k a_k {(x-x_0)}^{k-1} . \nonumber \]

Observe que el término correspondiente a\(k=0\) disappeared as it was constant. The radius of convergence of the differentiated series is the same as that of the original.

Ejemplo\(\PageIndex{5}\)

Demostremos que el exponencial\(y=e^x\) solves \(y'=y\). First write

\[y = e^x = \sum_{k=0}^\infty \frac{1}{k!} x^k . \nonumber \]

Ahora diferencie

\[y' = \sum_{k=1}^\infty k \frac{1}{k!} x^{k-1} =\sum_{k=1}^\infty \frac{1}{(k-1)!} x^{k-1} . \nonumber \]

Reindexamos la serie simplemente reemplazando\(k\) with \(k+1\). The series does not change, what changes is simply how we write it. After reindexing the series starts at \(k=0\) again.

\[\sum_{k=1}^\infty \frac{1}{(k-1)!} x^{k-1} =\sum_{k+1=1}^\infty \frac{1}{\bigl((k+1)-1\bigr)!} x^{(k+1)-1} =\sum_{k=0}^\infty \frac{1}{k!} x^k . \nonumber \]

Esa fue precisamente la serie power para\(e^x\) that we started with, so we showed that \(\frac{d}{dx} [ e^x ] = e^x\).

Las series de potencia convergente se pueden sumar y multiplicar juntas, y multiplicarse por constantes usando las siguientes reglas. Primero, podemos agregar series agregando término por término,

\[\left(\sum_{k=0}^\infty a_k {(x-x_0)}^k\right)+\left(\sum_{k=0}^\infty b_k {(x-x_0)}^k\right)=\sum_{k=0}^\infty (a_k+b_k) {(x-x_0)}^k . \nonumber \]

Podemos multiplicar por constantes,

\[\alpha \left(\sum_{k=0}^\infty a_k {(x-x_0)}^k\right)=\sum_{k=0}^\infty \alpha a_k {(x-x_0)}^k . \nonumber \]

También podemos multiplicar series juntas,

\[\left(\sum_{k=0}^\infty a_k {(x-x_0)}^k\right) \, \left(\sum_{k=0}^\infty b_k {(x-x_0)}^k\right)=\sum_{k=0}^\infty c_k {(x-x_0)}^k , \nonumber \]

donde\(c_k = a_0b_k + a_1 b_{k-1} + \cdots + a_k b_0\). The radius of convergence of the sum or the product is at least the minimum of the radii of convergence of the two series involved.

Serie de potencia para funciones racionales

Los polinomios son simplemente series de potencia finita. Es decir, un polinomio es una serie de potencias donde el\(a_k\) are zero for all \(k\) large enough. We can always expand a polynomial as a power series about any point \(x_0\) by writing the polynomial as a polynomial in \((x-x_0)\). For example, let us write \(2x^2-3x+4\) as a power series around \(x_0 = 1\):

\[2x^2-3x+4 = 3 + (x-1) + 2{(x-1)}^2 . \nonumber \]

En otras palabras\(a_0 = 3\), \(a_1 = 1\), \(a_2 = 2\), and all other \(a_k = 0\). To do this, we know that \(a_k = 0\) for all \(k \geq 3\) as the polynomial is of degree 2.

Escribimos\(a_0 + a_1(x-1) + a_2{(x-1)}^2\), we expand, and we solve for \(a_0\), \(a_1\), and \(a_2\). We could have also differentiated at \(x=1\)and used the Taylor series formula \(\eqref{eq:21}\).

Veamos las funciones racionales, es decir, las proporciones de polinomios. Un hecho importante es que una serie para una función solo define la función en un intervalo aunque la función se defina en otro lugar. Por ejemplo, para\(-1 < x < 1\) we have

\[\frac{1}{1-x} = \sum_{k=0}^\infty x^k = 1 + x + x^2 + \cdots \nonumber \]

Esta serie se llama la serie geométrica. La prueba de relación nos dice que el radio de convergencia es\(1\). The series diverges for \(x \leq -1\) and \(x \geq 1\), even though \(\frac{1}{1-x}\) is defined for all \(x \not= 1\).

Podemos usar la serie geométrica junto con reglas para la suma y multiplicación de series de potencia para expandir las funciones racionales alrededor de un punto, siempre y cuando el denominador no sea cero en\(x_0\). Note that as for polynomials, we could equivalently use the Taylor series expansion \(\eqref{eq:21}\).

Ejemplo\(\PageIndex{5}\)

Ampliar\(\frac{x}{1+2x+x^2}\) as a power series around the origin (\(x_0 = 0\)) and find the radius of convergence. First, write \(1+2x+x^2 = {(1+x)}^2 = {\bigl(1-(-x)\bigr)}^2\). Now we compute

\[\begin{align}\begin{aligned} \frac{x}{1+2x+x^2} &=x {\left( \frac{1}{1-(-x)} \right)}^2 \\ &=x { \left( \sum_{k=0}^{\infty} {(-1)}^k x^k \right)}^2 \\ &=x \left(\sum_{k=0}^{\infty} c_k x^k \right) \\ &= \sum_{k=0}^{\infty} c_k x^{k+1} ,\end{aligned}\end{align} \nonumber \]

donde usando la fórmula para el producto de serie obtenemos,\(c_0 = 1\), \(c_1 = -1 -1 = -2\), \(c_2 = 1+1+1 = 3\), etc \(\ldots\).

Por lo tanto

\[\frac{x}{1+2x+x^2}=\sum_{k=1}^\infty {(-1)}^{k+1} k x^k = x-2x^2+3x^3-4x^4+\cdots \nonumber \]

El radio de convergencia es de al menos 1. Utilizamos la prueba de ratio

\[\lim_{k\to\infty} \left\lvert \frac{a_{k+1}}{a_k} \right\rvert = \lim_{k\to\infty} \left\lvert \frac{{(-1)}^{k+2} (k+1)}{{(-1)}^{k+1}k} \right\rvert= \lim_{k\to\infty} \frac{k+1}{k}=1. \nonumber \]

Entonces el radio de convergencia es en realidad igual a 1.

Cuando la función racional es más complicada, también es posible utilizar el método de fracciones parciales. Por ejemplo, para encontrar la serie Taylor para\(\frac{x^3+x}{x^2-1}\), we write

\[ \frac{x^3+x}{x^2-1}=x + \frac{1}{1+x} - \frac{1}{1-x}=x + \sum_{k=0}^\infty {(-1)}^k x^k - \sum_{k=0}^\infty x^k= - x + \sum_{\substack{k=3 \\ k \text{ odd}}}^\infty (-2) x^k . \nonumber \]

Notas al pie

[1] Nombrado así por el matemático inglés Sir Brook Taylor (1685—1731).