7.2: Soluciones en serie de ODEs lineales de segundo orden

Supongamos que tenemos una ODE lineal homogénea de segundo orden de la forma

\[ p(x)y'' + q(x)y' + r(x)y = 0 \label{eq1} \]

Supongamos que\(p(x)\)\(q(x)\),, y\(r(x)\) son polinomios. Intentaremos una solución de la forma

\[ y = \sum_{k=0}^\infty a_k\left(x-x_o\right)^2 \nonumber \]

y resolver para\(a_k\) que el intente obtener una solución definida en algún intervalo alrededor\(x_o\).

Definición: Puntos Ordinarios y Singulares

El punto\(x_o\) se denomina punto ordinario si\(p(x_o) \neq 0\) en ODE homogéneo lineal de segundo orden de la forma en la Ecuación\ ref {eq1}. Es decir, las funciones

\[ \dfrac{q(x)}{p(x)} \quad\text{and}\quad \dfrac{r(x)}{p(x)} \nonumber \]

se definen para\(x\) cerca\(x_o\).

Si\( p(x_0)=0\), entonces decimos que\(x_o\) es un punto singular.

Manejar los puntos singulares es más difícil que los puntos ordinarios y así ahora nos enfocamos solo en los puntos ordinarios.

Ejemplo\(\PageIndex{1}\): Expansion around an Ordinary Point

Empecemos con un ejemplo muy sencillo

\[ y'' - y = 0 \nonumber \]

Vamos a probar una solución de serie de potencia cerca\(x_o=0\), que es un punto ordinario.

Solución

Cada punto es un punto ordinario de hecho, ya que la ecuación es coeficiente constante. Ya sabemos que debemos obtener exponenciales o el seno hiperbólico y coseno, pero pretendamos que no sabemos esto.

Intentamos

\[ y = \sum_{k=0}^\infty a_k x^k \nonumber \]

Si diferenciamos, el\( k=0 \) término es una constante y por lo tanto desaparece. Por lo tanto, obtenemos

\[ y' = \sum_{k=1}^\infty k\, a_k \, x^{k-1} \nonumber \]

Diferenciamos una vez más para obtener (ahora el\(k=1\) término desaparece)

\[ y'' = \sum_{k=2}^\infty k\, (k-1)\, a_k \, x^{k-2} \nonumber \]

Reindexamos la serie (reemplazamos\(k\) con\( k+2 \)) para obtener

\[ y'' = \sum_{k=0}^\infty (k+2)\, (k+1)\, a_{k+2} \, x^k \nonumber \]

Ahora enchufamos\(y\) y\(y''\) dentro de la ecuación diferencial.

\[\begin{align}\begin{aligned} 0 = y''-y &= \Biggl( \sum_{k=0}^\infty (k+2)(k+1) a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &= \sum_{k=0}^\infty \Bigl( (k+2) (k+1) a_{k+2} x^k - a_k x^k \Bigr) \\ &= \sum_{k=0}^\infty \bigl( (k+2)(k+1) a_{k+2} - a_k \bigr) x^k .\end{aligned}\end{align} \nonumber \]

Como\( y''-y\) se supone que es igual a 0, sabemos que los coeficientes de la serie resultante deben ser iguales a 0. Por lo tanto,

\[ (k+2) (k+1) a_{k+2} - a_k = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{a_k}{(k+2)(k+1)} . \nonumber \]

La ecuación anterior se denomina relación de recurrencia para los coeficientes de la serie de potencias. No importaba qué\(a_0\) o lo\(a_1\) era. Pueden ser arbitrarios. Pero una vez que elegimos\(a_0\) y\(a_1\), entonces todos los demás coeficientes están determinados por la relación de recurrencia.

Veamos cuáles deben ser los coeficientes. Primero,\(a_0\) y\(a_1\) son arbitrarios

\[ a_2 = \dfrac{a_0}{2}, \quad a_3 = \dfrac{a_1}{(3)(2)}, \quad a_4 = \dfrac{a_2}{(4)(3)} = \dfrac{a_0}{(4)(3)(2)}, \quad a_5 = \dfrac{a_3}{(5)(4)} = \dfrac{a_1}{(5)(4)(3)(2)}, \quad \ldots \nonumber \]

Así que notamos que para par\(k\), es decir\( k=2n\) conseguimos

\[ a_k = a_{2n} = \dfrac{a_o}{(2n)!} \nonumber \]

y por extraño\(k\) que es\( k=2n+1\) que tenemos

\[ a_k = a_{2n+1} = \dfrac{a_1}{(2n+1)!} \nonumber \]

Vamos a anotar la serie

\[y =\sum_{k=0}^\infty a_k x^k= \sum_{n=0}^\infty \left( \dfrac{a_0}{(2n)!} \,x^{2n} +\dfrac{a_1}{(2n+1)!} \,x^{2n+1} \right) =a_0 \sum_{n=0}^\infty \dfrac{1}{(2n)!} \,x^{2n}+a_1 \sum_{n=0}^\infty \dfrac{1}{(2n+1)!} \,x^{2n+1} . \nonumber \]

Reconocemos las dos series como el seno hiperbólico y el coseno. Por lo tanto,

\[ y= a_o \, \text{cosh} \, x + a_1\, \text{sinh}\, x \nonumber \]

Por supuesto, en general no podremos reconocer la serie que aparece, ya que por lo general no habrá ninguna función elemental que coincida con ella. En ese caso estaremos contentos con la serie.

Ejemplo\(\PageIndex{2}\)

Hagamos un ejemplo más complejo. Supongamos que deseamos resolver la ecuación de Airy \(^{1}\), es decir

\[ y'' - xy = 0 \nonumber \]

cerca del punto\( x_0 = 0 \), que es un punto ordinario.

Intentamos

\[ y = \sum_{k=0}^{\infty} a_k x^k \nonumber \]

Diferenciamos dos veces (como arriba) para obtener

\[ y'' = \sum_{k=2}^{\infty} k(k-1)a_k x^{k-2} \nonumber \]

Nos conectamos\(y\) a la ecuación

\[\begin{align}\begin{aligned} 0 = y''-xy &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)-x \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)-\Biggl( \sum_{k=0}^\infty a_k x^{k+1} \Biggr) .\end{aligned}\end{align} \nonumber \]

Reindexamos para que las cosas sean más fáciles de sumar

\[\begin{align}\begin{aligned} 0 = y''-xy &= \Biggl( 2 a_2 + \sum_{k=1}^\infty (k+2)\,(k+1) \, a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=1}^\infty a_{k-1} x^k \Biggr) . \\ &= 2 a_2 + \sum_{k=1}^\infty \Bigl( (k+2)\,(k+1) \, a_{k+2} - a_{k-1} \Bigr) \, x^k .\end{aligned}\end{align} \nonumber \]

De nuevo\( y'' - xy\) se supone que es 0 así que primero notamos eso\(a_2 = 0 \) y también

\[ (k+2)\,(k+1) \,a_{k+2} - a_{k-1} = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{a_{k-1}}{(k+2)(k+1)} . \nonumber \]

Ahora saltamos en pasos de tres. Primero notamos que ya que\(a_2 = 0\) debemos tener eso\(a_5 = 0\),\(a_8 = 0\),\(a_{11}=0\),,\(\ldots\) etc. En general\(a_{3n+2} =0\). Las constantes\(a_0\) y\(a_1\) son arbitrarias y obtenemos

\[a_3 = \dfrac{a_0}{(3)(2)}, \quad a_4 = \dfrac{a_1}{(4)(3)}, \quad a_6 = \dfrac{a_3}{(6)(5)} = \dfrac{a_0}{(6)(5)(3)(2)}, \quad a_7 = \dfrac{a_4}{(7)(6)} = \dfrac{a_1}{(7)(6)(4)(3)}, \quad \ldots \nonumber \]

Porque\(a_k\) donde\(k\) es un múltiplo de\(3\), es decir\(k=3n\) notamos que

\[a_{3n} = \dfrac{a_0}{(2)(3)(5)(6) \cdots (3n-1)(3n)} . \nonumber \]

Para\(a_k\) donde\(k = 3n+1\), nos damos cuenta

\[a_{3n+1} = \dfrac{a_1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} . \nonumber \]

Es decir, si escribimos la serie porque\(y\) notamos que tiene dos partes

\[\begin{align}\begin{aligned} y &=\left( a_0 + \dfrac{a_0}{6} x^3 + \dfrac{a_0}{180} x^6 + \cdots + \dfrac{a_0}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots \right) \\ & \phantom{=}+\left( a_1 x + \dfrac{a_1}{12} x^4 + \dfrac{a_1}{504} x^7 + \cdots + \dfrac{a_1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots \right) \\ &=a_0 \left(1 + \dfrac{1}{6} x^3 + \dfrac{1}{180} x^6 + \cdots + \dfrac{1}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots \right) \\ &\phantom{=}+a_1\left(x + \dfrac{1}{12} x^4 + \dfrac{1}{504} x^7 + \cdots +\dfrac{1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots \right) .\end{aligned}\end{align} \nonumber \]

Definimos

\[\begin{align}\begin{aligned} y_1(x) &= 1 + \dfrac{1}{6} x^3 + \dfrac{1}{180} x^6 + \cdots + \dfrac{1}{(2)(3)(5)(6) \cdots (3n-1)(3n)} x^{3n} + \cdots, \\y_2(x) &= x + \dfrac{1}{12} x^4 + \dfrac{1}{504} x^7 + \cdots + \dfrac{1}{(3)(4)(6)(7) \cdots (3n)(3n+1)} x^{3n+1} + \cdots ,\end{aligned}\end{align} \nonumber \]

y escribir la solución general a la ecuación como\(y(x)= a_0 y_1(x) + a_1 y_2(x)\). Observe de la serie power que\(y_1(0) = 1\) y\(y_2(0) = 0\). También,\(y_1'(0) = 0\) y\(y_2'(0) = 1\). Por lo tanto\(y(x)\) es una solución que satisface las condiciones iniciales\(y(0) = a_0\) y\(y'(0) = a_1\).

Figura\(\PageIndex{1}\): Las dos soluciones\(y_{1}\) y\(y_{2}\) la ecuación de Airy.

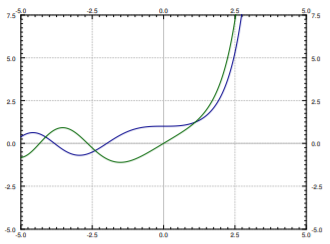
Las funciones\(y_1\) and \(y_2\) cannot be written in terms of the elementary functions that you know. See Figure \(\PageIndex{1}\) para la trama de las soluciones\(y_1\) and \(y_2\). These functions have many interesting properties. For example, they are oscillatory for negative \(x\) (like solutions to \(y''+y=0\)) and for positive \(x\) they grow without bound (like solutions to \(y''-y=0\)).

A veces una solución puede llegar a ser un polinomio.

Ejemplo\(\PageIndex{3}\): Hermite Equation

Encontremos una solución a la llamada ecuación de orden de Hermite\(n\)\(^{2}\) is the equation

\[ y'' -2xy' + 2n y = 0 . \nonumber \]

Encuentre una solución alrededor del punto\(x_0 = 0\).

Solución

Intentamos

\[y = \sum_{k=0}^\infty a_k x^k . \nonumber \]

Diferenciamos (como arriba) para obtener

\[\begin{align}\begin{aligned} y' =& \sum_{k=1}^\infty k a_k x^{k-1} , \\ y'' &= \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} .\end{aligned}\end{align} \nonumber \]

Ahora nos conectamos a la ecuación

\[\begin{align}\begin{aligned} 0 &= y''-2xy'+2ny \\ &= \Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr) -2x \Biggl( \sum_{k=1}^\infty k a_k x^{k-1} \Biggr)+2n \Biggl( \sum_{k=0}^\infty a_k x^k \Biggr) \\ &=\Biggl( \sum_{k=2}^\infty k\,(k-1) \, a_k x^{k-2} \Biggr)- \Biggl( \sum_{k=1}^\infty 2k a_k x^k \Biggr) + \Biggl( \sum_{k=0}^\infty 2n a_k x^k \Biggr) \\ &= \Biggl(2a_2+ \sum_{k=1}^\infty (k+2)\,(k+1) \, a_{k+2} x^k \Biggr) - \Biggl( \sum_{k=1}^\infty 2k a_k x^k \Biggr) + \Biggl( 2na_0 + \sum_{k=1}^\infty 2n a_k x^k \Biggr) \\ &=2a_2+2na_0+ \sum_{k=1}^\infty \bigl( (k+2)\,(k+1) \, a_{k+2} - 2ka_k + 2n a_k \bigr) x^k .\end{aligned}\end{align} \nonumber \]

Como\(y''-2xy'+2ny = 0\) we have

\[(k+2)\,(k+1) \, a_{k+2} + ( - 2k+ 2n) a_k = 0 , \qquad \text{or} \qquad a_{k+2} = \dfrac{(2k-2n)}{(k+2)(k+1)} a_k . \nonumber \]

Esta relación de recurrencia en realidad incluye\(a_2 = -na_0\) (which comes about from \(2a_2+2na_0 = 0\)). Again \(a_0\) and \(a_1\) are arbitrary.

\[\begin{align}\begin{aligned} a_2 &= \dfrac{-2n}{(2)(1)}a_0, \qquad a_3 = \dfrac{2(1-n)}{(3)(2)} a_1, \\ a_4& = \dfrac{2(2-n)}{(4)(3)} a_2 = \dfrac{2^2(2-n)(-n)}{(4)(3)(2)(1)} a_0 , \\ a_5& = \dfrac{2(3-n)}{(5)(4)} a_3 = \dfrac{2^2(3-n)(1-n)}{(5)(4)(3)(2)} a_1 , \quad \ldots\end{aligned}\end{align} \nonumber \]

Separemos los coeficientes par e impar. Nos encontramos con que

\[\begin{align}\begin{aligned} a_{2m} &=\dfrac{2^m(-n)(2-n)\cdots(2m-2-n)}{(2m)!} , \\ a_{2m+1} &=\dfrac{2^m(1-n)(3-n)\cdots(2m-1-n)}{(2m+1)!} .\end{aligned}\end{align} \nonumber \]

Anote las dos series, una con los poderes pares y otra con la impar.

\[\begin{align}\begin{aligned} y_1(x) &= 1+\dfrac{2(-n)}{2!} x^2 + \dfrac{2^2(-n)(2-n)}{4!} x^4 + \dfrac{2^3(-n)(2-n)(4-n)}{6!} x^6 + \cdots , \\ y_2(x) &= x+\dfrac{2(1-n)}{3!} x^3 + \dfrac{2^2(1-n)(3-n)}{5!} x^5 + \dfrac{2^3(1-n)(3-n)(5-n)}{7!} x^7 + \cdots .\end{aligned}\end{align} \nonumber \]

Luego escribimos

\[y(x) = a_0 y_1(x) + a_1 y_2(x) . \nonumber \]

También notamos que si\(n\) is a positive even integer, then \(y_1(x)\) is a polynomial as all the coefficients in the series beyond a certain degree are zero. If \(n\) is a positive odd integer, then \(y_2(x)\) is a polynomial. For example, if \(n=4\), then

\[ y_1(x) = 1 + \dfrac{2(-4)}{2!} x^2 + \dfrac{2^2(-4)(2-4)}{4!} x^4= 1 - 4x^2 + \dfrac{4}{3} x^4 . \nonumber \]

Notas al pie

[1] Nombrado así por el matemático inglés Sir George Biddell Airy (1801 — 1892).

[2] Nombrado así por el matemático francés Charles Hermite (1822—1901).