8.3: Aplicaciones de sistemas no lineales

En esta sección estudiamos dos ejemplos muy estándar de sistemas no lineales. Primero, observamos la ecuación del péndulo no lineal. Vimos la linealización de la ecuación del péndulo antes, pero notamos que solo era válida para ángulos pequeños y tiempos cortos. Ahora nos enteramos de lo que sucede para ángulos grandes. A continuación, observamos la ecuación depredador-presa, que encuentra diversas aplicaciones en el modelado de problemas en biología, química, economía y otros lugares.

Péndulo

El primer ejemplo que estudiamos es la ecuación del péndulo\(\theta''+\frac{g}{L} \sin \theta = 0\). Aquí,\(\theta\) está el desplazamiento angular,\(g\) es la aceleración gravitacional, y\(L\) es la longitud del péndulo. En esta ecuación hacemos caso omiso de la fricción, por lo que estamos hablando de un péndulo idealizado.

Figura\(\PageIndex{1}\)

Esta ecuación es una ecuación conservadora, por lo que podemos usar nuestro análisis de ecuaciones conservadoras de la sección anterior. Cambiemos la ecuación a un sistema bidimensional en variables\((\theta,\omega)\) introduciendo la nueva variable\(\omega\):\[\begin{bmatrix} \theta \\ \omega \end{bmatrix} ' = \begin{bmatrix} \omega \\ - \frac{g}{L} \sin \theta \end{bmatrix} . \nonumber \]

Los puntos críticos de este sistema son cuándo\(\omega = 0\) y\(-\frac{g}{L} \sin \theta = 0\), o en otras palabras si\(\sin \theta = 0\). Entonces los puntos críticos son cuándo\(\omega = 0\) y\(\theta\) es un múltiplo de\(\pi\). Es decir, los puntos son\(\ldots (-2\pi,0), (-\pi,0), (0,0), (\pi,0), (2\pi,0) \ldots\). Si bien hay infinitamente muchos puntos críticos, todos están aislados. Calculemos la matriz jacobiana:\[\begin{bmatrix} \frac{\partial}{\partial \theta} \Bigl( \omega \Bigr) & \frac{\partial}{\partial \omega} \Bigl( \omega \Bigr) \\ \frac{\partial}{\partial \theta} \Bigl( - \frac{g}{L} \sin \theta \Bigr) & \frac{\partial}{\partial \omega} \Bigl( - \frac{g}{L} \sin \theta \Bigr) \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ - \frac{g}{L} \cos \theta & 0 \end{bmatrix} . \nonumber \]

Para las ecuaciones conservadoras, existen dos tipos de puntos críticos. Ya sea centros estables, o puntos de sillín. Los valores propios de la matriz jacobiana son\(\lambda = \pm \sqrt{-\frac{g}{L}\cos \theta}\).

Los valores propios van a ser reales cuando\(\cos \theta < 0\). Esto sucede en los múltiplos impares de\(\pi\). Los valores propios van a ser puramente imaginarios cuando\(\cos \theta > 0\). Esto sucede en los múltiplos pares de\(\pi\). Por lo tanto, el sistema tiene un centro estable en los puntos\(\ldots (-2\pi,0), (0,0), (2\pi,0) \ldots\), y tiene un sillín inestable en los puntos\(\ldots (-3\pi,0), (-\pi,0), (\pi,0), (3\pi,0) \ldots\). Mira el diagrama de fases en la Figura\(\PageIndex{2}\), donde por simplicidad dejamos\(\frac{g}{L} = 1\).

Figura\(\PageIndex{2}\): Diagrama del plano de fase y algunas trayectorias de la ecuación del péndulo no lineal.

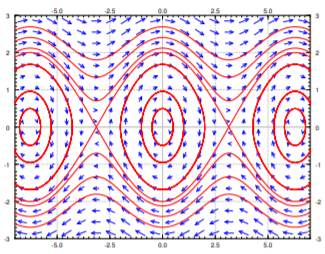
En la ecuación linealizada tenemos sólo un único punto crítico, el centro en\((0,0)\). Ahora vemos más claramente a qué nos referíamos cuando dijimos que la linealización es buena para ángulos pequeños. El eje horizontal es el ángulo de deflexión. El eje vertical es la velocidad angular del péndulo. Supongamos que comenzamos en\(\theta = 0\) (sin deflexión), y comenzamos con una velocidad angular pequeña\(\omega\). Entonces la trayectoria sigue circulando alrededor del punto crítico\((0,0)\) en un círculo aproximado. Esto corresponde a breves oscilaciones del péndulo de ida y vuelta. Cuando\(\theta\) se mantiene pequeño, las trayectorias realmente parecen círculos y por lo tanto están muy cerca de nuestra linealización.

Cuando le damos al péndulo un empujón lo suficientemente grande, cruza la parte superior y sigue girando alrededor de su eje. Este comportamiento corresponde a las curvas onduladas que no cruzan el eje horizontal en el diagrama de fases. Supongamos que miramos las curvas superiores, cuando la velocidad angular\(\omega\) es grande y positiva. Entonces el péndulo va alrededor y alrededor de su eje. La velocidad va a ser grande cuando el péndulo está cerca del fondo, y la velocidad es la más pequeña cuando el péndulo está cerca de la parte superior de su bucle.

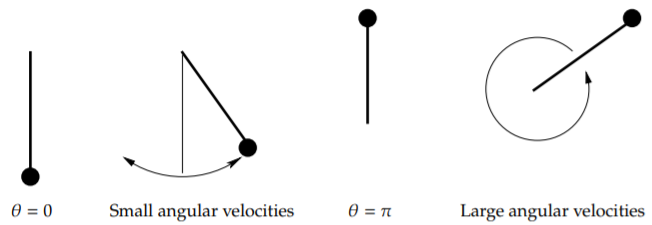
En cada punto crítico, hay una solución de equilibrio. Considera la solución\(\theta = 0\); el péndulo no se mueve y está colgando recto hacia abajo. Este es un lugar estable para que esté el péndulo, de ahí que este sea un equilibrio estable.

El otro tipo de solución de equilibrio está en el punto inestable, por ejemplo\(\theta = \pi\). Aquí el péndulo está boca abajo. Seguro puedes equilibrar el péndulo de esta manera y se quedará, pero este es un equilibrio inestable. Incluso el empujón más pequeño hará que el péndulo comience a balancearse salvajemente.

Consulte la Figura\(\PageIndex{3}\) para ver un diagrama. El primer cuadro es el equilibrio estable\(\theta = 0\). La segunda imagen corresponde a las del diagrama de fases alrededor\(\theta =0\) cuando la velocidad angular es pequeña. El siguiente cuadro es el equilibrio inestable\(\theta = \pi\). El último cuadro corresponde a las líneas onduladas para grandes velocidades angulares.

Figura\(\PageIndex{3}\): Diversas posibilidades para el movimiento del péndulo.

La cantidad

\[\frac{1}{2} \omega^2 - \frac{g}{L} \cos \theta \nonumber \]

es conservado por cualquier solución. Esta es la energía o la hamiltoniana del sistema.

Tenemos una ecuación conservadora y así (ejercicio) las trayectorias vienen dadas por

\[\omega = \pm \sqrt{ \frac{2g}{L} \cos \theta + C} , \nonumber \]

para diversos valores de\(C\). Let us look at the initial condition of \((\theta_0,0)\), that is, we take the pendulum to angle \(\theta_0\), and just let it go (initial angular velocity 0). We plug the initial conditions into the above and solve for \(C\) to obtain

\[C = - \frac{2g}{L} \cos \theta_0 . \nonumber \]

Así, la expresión de la trayectoria es

\[\omega = \pm \sqrt{ \frac{2g}{L}} \sqrt{ \cos \theta - \cos \theta_0 } . \nonumber \]

Averiguemos el periodo. Es decir, el tiempo que tarda el péndulo en oscilar de un lado a otro. Nos damos cuenta de que la oscilación sobre el origen en el plano de fase es simétrica tanto con respecto a la\(\theta\) and the \(\omega\) axis. That is, in terms of \(\theta\), the time it takes from \(\theta_0\) to \(-\theta_0\) is the same as it takes from \(-\theta_0\) back to \(\theta_0\). Furthermore, the time it takes from \(-\theta_0\) to \(0\) is the same as to go from \(0\) to \(\theta_0\). Therefore, let us find how long it takes for the pendulum to go from angle 0 to angle \(\theta_0\), which is a quarter of the full oscillation and then multiply by 4.

Nos damos cuenta esta vez al encontrar\(\frac{dt}{d\theta}\) and integrating from \(0\) to \(\omega_0\). The period is four times this integral. Let us stay in the region where \(\omega\) is positive. Since \(\omega = \frac{d\theta}{dt}\), inverting we get

\[\frac{dt}{d\theta} = \sqrt{\frac{L}{2g}} \frac{1}{\sqrt{\cos \theta - \cos \theta_0 }} . \nonumber \]

Por lo tanto, el periodo\(T\) is given by

\[T = 4 \sqrt{\frac{L}{2g}} \int_0^{\theta_0} \frac{1}{\sqrt{\cos \theta - \cos \theta_0 }}\, d\theta . \nonumber \]

La integral es una integral impropia, y en general no podemos evaluarla simbólicamente. Debemos recurrir a la aproximación numérica si queremos calcular un particular\(T\).

Recordar de la Sección 2.4, la ecuación linealizada\(\theta''+\frac{g}{L}\theta = 0\) has period

\[T_{\text{linear}} = 2\pi \sqrt{\frac{L}{g}} . \nonumber \]

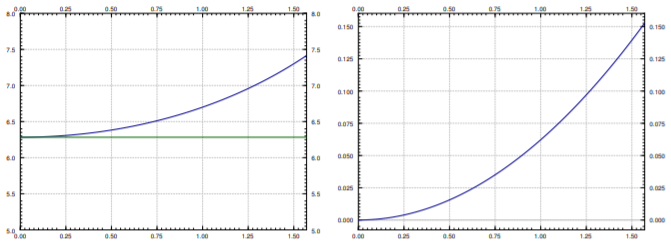
Trazamos\(T\), \(T_{\text{linear}}\), and the relative error \(\frac{T-T_{\text{linear}}}{T}\) in Figure \(\PageIndex{4}\). The relative error says how far is our approximation from the real period percentage-wise. Note that \(T_{\text{linear}}\) is simply a constant, it does not change with the initial angle \(\theta_0\). The actual period \(T\) gets larger and larger as \(\theta_0\) gets larger. Notice how the relative error is small when \(\theta_0\) is small. It is still only \(15\%\) when \(\theta_0 = \frac{\pi}{2}\), that is, a 90 degree angle. The error is \(3.8\%\) when starting at \(\frac{\pi}{4}\), a 45 degree angle. At a 5 degree initial angle, the error is only \(0.048 \%\).

Figura\(\PageIndex{4}\): La gráfica de\(T\) y\(T_{\text{linear}}\) con\(\frac{g}{L}=1\) (izquierda), y la gráfica del error relativo\(\frac{T-T_{\text{linear}}}{T}\) (derecha), para\(\theta_{0}\) entre\(0\) y\(\frac{\pi}{2}\).

W hile no es inmediatamente obvio por la fórmula, es cierto que

\[\lim_{\theta_0 \uparrow \pi} T = \infty . \nonumber \]

Es decir, el periodo va al infinito a medida que el ángulo inicial se acerca al punto de equilibrio inestable. Entonces, si ponemos el péndulo casi boca abajo puede pasar mucho tiempo antes de que se baje. Esto es consistente con el comportamiento limitante, donde el péndulo exactamente al revés nunca hace una oscilación, por lo que podríamos pensar en eso como un período infinito.

Sistemas Predator-Presa o Lotka-Volterra

Una de las aplicaciones simples más comunes de los sistemas no lineales son los llamados \(^{1}\)sistemas depredador-presa o Lotka -Volterra. Por ejemplo, estos sistemas surgen cuando dos especies interactúan, una como presa y otra como depredador. Entonces no es de sorprender que las ecuaciones también vean aplicaciones en economía. El sistema también surge en reacciones químicas. En biología, este sistema de ecuaciones explica las variaciones periódicas naturales de poblaciones de diferentes especies en la naturaleza. Antes de la aplicación de ecuaciones diferenciales, estas variaciones periódicas en la población desconcertaron a los biólogos.

Mantenemos con el ejemplo clásico de liebres y zorros en un bosque, es el más fácil de entender. \[\begin{align}\begin{aligned} & x = \# \text{ of hares (the prey),} \\ & y = \# \text{ of foxes (the predator).} \end{aligned}\end{align} \nonumber \]Cuando hay muchas liebres, hay mucha comida para los zorros, por lo que la población de zorros crece. No obstante, cuando la población de zorros crece, los zorros comen más liebres, así que cuando hay muchos zorros, la población de liebre debería bajar, y viceversa. El modelo Lotka—Volterra propone que este comportamiento es descrito por el sistema de ecuaciones\[\begin{align}\begin{aligned} & x' = (a-by)x, \\ & y' = (cx-d)y, \end{aligned}\end{align} \nonumber \] donde\(a,b,c,d\) se encuentran algunos parámetros que describen la interacción de los zorros y las liebres \(^{2}\). En este modelo, todos estos son números positivos.

Analicemos la idea detrás de este modelo. El modelo es una idea un poco más complicada basada en el modelo poblacional exponencial. Primero expandirse, Se espera que\[x' = (a-by)x = ax - byx . \nonumber \] las liebres simplemente crezcan exponencialmente en ausencia de zorros, es ahí donde entra el\(ax\) término, el crecimiento de la población es proporcional a la propia población. Estamos asumiendo que las liebres siempre encuentran suficiente comida y tienen suficiente espacio para reproducirse. Sin embargo, hay otro componente\(-byx\), es decir, la población también está disminuyendo proporcionalmente al número de zorros. Juntos podemos escribir la ecuación como\((a-by)x\), así es como crecimiento exponencial o decaimiento pero la constante depende del número de zorros.

La ecuación para zorros es muy similar, expandirse de nuevo\[y' = (cx-d)y = cxy-dy . \nonumber \] Los zorros necesitan alimento (liebres) para reproducirse: cuanto más alimento, mayor es la tasa de crecimiento, de ahí el\(cxy\) término. Por otro lado, hay muertes naturales en la población de zorros, y de ahí el\(-dy\) término.

Sin más dilación, comencemos con un ejemplo explícito. Supongamos que las ecuaciones son\[x' = (0.4-0.01y)x, \qquad y' = (0.003x-0.3)y . \nonumber \] Ver Figura\(\PageIndex{5}\) para el retrato de fase. En este ejemplo tiene sentido trazar también\(x\) y\(y\) como gráficas con respecto al tiempo. Por lo tanto, la segunda gráfica de la Figura\(\PageIndex{5}\) es la gráfica de\(x\) y\(y\) sobre el eje vertical (la presa\(x\) es la línea más delgada con picos más altos), contra el tiempo en el eje horizontal. La solución particular graficada fue con condiciones iniciales de\(20\) zorros y\(50\) liebres.

Figura\(\PageIndex{5}\): El retrato de fase (izquierda) y gráficas de\(x\) y\(y\) para una solución de muestra (derecha).

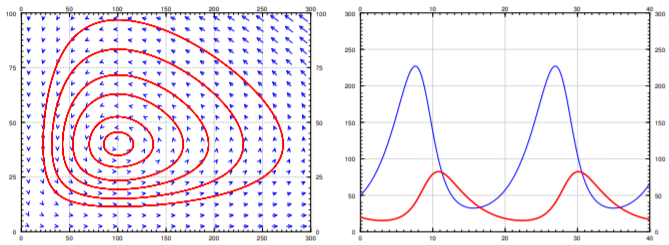
Analicemos lo que vemos en las gráficas. Trabajamos en el ámbito general en lugar de poner números específicos. Empezamos por encontrar los puntos críticos. Establecer\((a-by)x = 0\), y\((cx-d)y = 0\). La primera ecuación se satisface si cualquiera\(x=0\) o\(y=\frac{a}{b}\). Si\(x=0\), la segunda ecuación implica\(y=0\). Si\(y= \frac{a}{b}\), la segunda ecuación implica\(x=\frac{d}{c}\). Hay dos equilibrios:\((0,0)\) cuando no hay animales en absoluto, y en\((\frac{d}{c},\frac{a}{b})\). En nuestro ejemplo específico\(x = \frac{d}{c} = 100\), y\(y = \frac{a}{b} = 40\). Este es el punto donde hay 100 liebres y 40 zorros.

Calculamos la matriz jacobiana:\[\begin{bmatrix} a-by & -bx \\ cy & cx-d \end{bmatrix} . \nonumber \] Al origen\((0,0)\) obtenemos la matriz\(\left[ \begin{smallmatrix} a & 0 \\ 0 & -d \end{smallmatrix} \right]\), por lo que los valores propios son\(a\) y\(-d\), de ahí reales y de signos opuestos. Entonces el punto crítico en el origen es una silla de montar. Esto tiene sentido. Si empezabas con algunos zorros pero sin liebres, entonces los zorros se extinguirían, es decir, te acercarías al origen. Si empezabas sin zorros y algunas liebres, entonces las liebres seguirían multiplicándose sin control, y así te alejarías del origen.

Bien, ¿qué tal el otro punto crítico en\((\frac{d}{c},\frac{a}{b})\). Aquí la matriz jacobiana se convierte\[\begin{bmatrix} 0 & -\frac{bd}{c} \\ \frac{ac}{b} & 0 \end{bmatrix} . \nonumber \] en Los valores propios satisfacen\(\lambda^2 + ad = 0\). En otras palabras,\(\lambda = \pm i \sqrt{ad}\). Siendo los valores propios puramente imaginarios, estamos en el caso en el que no podemos decidir del todo usando solo linealización. Podríamos tener un centro estable, un fregadero espiral o una fuente espiral. Es decir, el equilibrio podría ser asintóticamente estable, estable o inestable. Por supuesto que te di una foto arriba que parece implicar que es un centro estable. Pero nunca confíes solo en una imagen. Quizás las oscilaciones son cada vez más grandes, pero sólo muy lentamente. Por supuesto esto sería malo ya que implicaría que algo va a salir mal con nuestra población tarde o temprano. Y sólo graficé un ejemplo muy específico con trayectorias muy específicas.

¿Cómo podemos estar seguros de que estamos en la situación estable? Como dijimos antes, en el caso de los valores propios puramente imaginarios, tenemos que hacer un poco más de trabajo. Anteriormente encontramos que para los sistemas conservadores, había cierta cantidad que se conservaba en las trayectorias, y de ahí que las trayectorias tuvieran que ir en bucles cerrados. Podemos usar una técnica similar aquí. Sólo tenemos que averiguar cuál es la cantidad conservada. Después de algún ensayo y error encontramos que la constante\[C = \frac{y^a x^d}{e^{cx+by}} = y^a x^d e^{-cx-by} \nonumber \] se conserva. Tal cantidad se llama la constante del movimiento. Comprobemos\(C\) realmente es una constante de movimiento. ¿Cómo verificamos, dices? Bueno, una constante es algo que no cambia con el tiempo, así que vamos a calcular la derivada con respecto al tiempo:\[C' = a y^{a-1}y' x^d e^{-cx-by} + y^a d x^{d-1} x' e^{-cx-by} + y^a x^d e^{-cx-by} (-cx'-by') . \nonumber \] Nuestras ecuaciones nos dan qué\(x'\) y\(y'\) son así que vamos a enchufarlas:

\[\begin{align}\begin{aligned} C' & = a y^{a-1} (cx-d)y x^d e^{-cx-by} + y^a d x^{d-1} (a-by)x e^{-cx-by} \\ & \phantom{mm} + y^a x^d e^{-cx-by} \bigl(-c(a-by)x-b(cx-d)y\bigr) \\ & = y^a x^d e^{-cx-by} \Bigl( a (cx-d) + d (a-by) + \bigl(-c(a-by)x-b(cx-d)y\bigr) \Bigr) \\ & = 0 . \end{aligned}\end{align} \nonumber \]Entonces a lo largo de las trayectorias\(C\) es constante. De hecho, la expresión nos\(C = \frac{y^a x^d}{e^{cx+by}}\) da una ecuación implícita para las trayectorias. En cualquier caso, una vez que hayamos encontrado esta constante de movimiento, debe ser cierto que las trayectorias son curvas simples, es decir, las curvas de nivel de\(\frac{y^a x^d}{e^{cx+by}}\). Resulta, el punto crítico en\((\frac{d}{c},\frac{a}{b})\) es un máximo para\(C\) (dejado como ejercicio). Entonces\((\frac{d}{c},\frac{a}{b})\) es un punto de equilibrio estable, y no tenemos que preocuparnos de que los zorros y liebres se extingan o sus poblaciones exploten.

Una mancha en este maravilloso modelo es que el número de zorros y liebres son cantidades discretas y estamos modelando con variables continuas. Nuestro modelo no tiene ningún problema con que haya\(0.1\) zorro en el bosque por ejemplo, mientras que en la realidad eso no tiene sentido. La aproximación es razonable siempre y cuando el número de zorros y liebres sea grande, pero no tiene mucho sentido para números pequeños. Hay que tener cuidado al interpretar cualquier resultado de tal modelo.

Una consecuencia interesante (quizás contraintuitiva) de este modelo es que agregar animales al bosque podría llevar a la extinción, porque las variaciones se volverán demasiado grandes, y una de las poblaciones se acercará a cero. Por ejemplo, supongamos que hay\(20\) zorros y\(50\) liebres como antes, pero ahora traemos más zorros, llevando su número a\(200\). Si ejecutamos el cálculo, encontramos que el número de liebres se desplomará a poco más que\(1\) liebre en todo el bosque. En realidad eso muy probablemente signifique que las liebres se extinguen, y luego los zorros morirán así como no tendrán nada para comer.

Demostrar que un sistema de ecuaciones tiene una solución estable puede ser un problema muy difícil. Cuando Isaac Newton expuso sus leyes de movimientos planetarios, demostró que un solo planeta orbitando un solo sol es un sistema estable. Pero cualquier sistema solar con más que\(1\) planeta resultó realmente muy difícil. De hecho, dicho sistema se comporta caóticamente (ver Sección 8.5), lo que significa que pequeños cambios en las condiciones iniciales conducen a resultados muy diferentes a largo plazo. A partir de la experimentación numérica y las mediciones, sabemos que la tierra no volará hacia el espacio vacío ni chocará contra el sol, durante al menos algunos millones de años más o menos. Pero no sabemos qué pasa más allá de eso.

Notas al pie

[1] Nombrado así por el matemático, químico y estadístico estadounidense Alfred James Lotka (1880—1949) y el matemático y físico italiano Vito Volterra (1860—1940).

[2] Esta interacción no termina bien para la liebre.