2.2: Ecuaciones separables
- Page ID
- 115132
Una ecuación diferencial de primer orden es separable si se puede escribir como
\[\label{eq:2.2.1} h(y)y'=g(x),\]
donde el lado izquierdo es un producto de\(y'\) y una función de\(y\) y el lado derecho es una función de\(x\). Reescribir una ecuación diferencial separable en esta forma se llama separación de variables. En la Sección 2.1, se utilizó la separación de variables para resolver ecuaciones lineales homogéneas. En esta sección aplicaremos este método a ecuaciones no lineales.
Para ver cómo resolver la Ecuación\ ref {eq:2.2.1}, primero supongamos que\(y\) es una solución. Dejar\(G(x)\) y\(H(y)\) ser antiderivados de\(g(x)\) y\(h(y)\); es decir,
\[\label{eq:2.2.2} H'(y)=h(y) \quad \text{and} \quad G'(x)=g(x).\]
Entonces, a partir de la regla de la cadena,
\[{d\over dx}H(y(x))=H'(y(x))y'(x)=h(y)y'(x).\nonumber \]
Por lo tanto, la ecuación\ ref {eq:2.2.1} es equivalente a
\[{d\over dx}H(y(x))={d\over dx}G(x).\nonumber \]
Integrar ambos lados de esta ecuación y combinar las constantes de rendimientos de integración
\[\label{eq:2.2.3} H(y(x))=G(x)+c.\]
Aunque derivamos esta ecuación en el supuesto de que\(y\) es una solución de la Ecuación\ ref {eq:2.2.1}, ahora podemos verla de manera diferente: Cualquier función diferenciable\(y\) que satisfaga la Ecuación\ ref {eq:2.2.3} para alguna constante\(c\) es una solución de la Ecuación\ ref {eq:2.2.1}. Para ver esto, diferenciamos ambos lados de la Ecuación\ ref {eq:2.2.3}, usando la regla de cadena de la izquierda, para obtener
\[H'(y(x))y'(x)=G'(x), \nonumber \]
que es equivalente a
\[h(y(x))y'(x)=g(x) \nonumber \]
debido a la Ecuación\ ref {eq:2.2.2}.
En conclusión, para resolver la Ecuación\ ref {eq:2.2.1} basta con encontrar funciones\(G=G(x)\) y\(H=H(y)\) que satisfagan la Ecuación\ ref {eq:2.2.2}. Entonces cualquier función diferenciable\(y=y(x)\) que satisfaga la Ecuación\ ref {eq:2.2.3} es una solución de la Ecuación\ ref {eq:2.2.1}.
Resolver la ecuación
\[y'=x(1+y^2). \nonumber \]
Solución
Separación de rendimientos de variables
\[{y'\over 1+y^2}=x. \nonumber \]
Integración de rendimientos
\[\tan^{-1}y={x^2\over2}+c \nonumber \]
Por lo tanto
\[y=\tan\left({x^2\over2}+c\right). \nonumber \]
- Resolver la ecuación\[\label{eq:2.2.4} y'=-{x\over y}.\]
- Resolver el problema de valor inicial\[\label{eq:2.2.5} y'=-{x\over y}, \quad y(1)=1.\]
- Resolver el problema de valor inicial\[\label{eq:2.2.6} y'=-{x\over y}, \quad y(1)=-2.\]
Solución a
Separar variables en Ecuación\ ref {eq:2.2.4} rendimientos
\[yy'=-x. \nonumber \]
Integración de rendimientos
\[{y^2\over2}=-{x^2\over2}+c, \quad \text{or equivalently} \quad x^2+y^2=2c. \nonumber \]
La última ecuación muestra que\(c\) debe ser positiva si\(y\) va a ser una solución de la Ecuación\ ref {eq:2.2.4} en un intervalo abierto. Por lo tanto dejamos\(2c=a^2\) (con\(a > 0\)) y reescribimos la última ecuación como
\[\label{eq:2.2.7} x^2+y^2=a^2.\nonumber\]
Esta ecuación tiene dos soluciones diferenciables para\(y\) en términos de\(x\):
\[\label{eq:2.2.8} y=\phantom{-} \sqrt{a^2-x^2}, \quad -a < x < a,\nonumber\]
y
\[\label{eq:2.2.9} y= - \sqrt{a^2-x^2}, \quad -a < x < a.\]
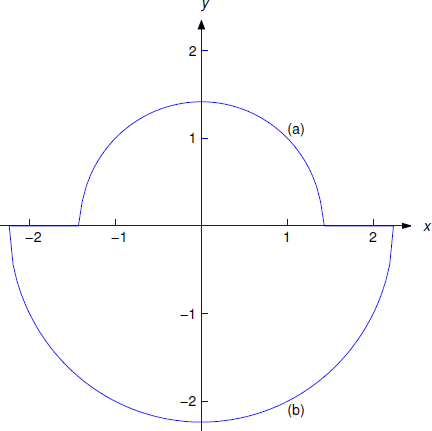
Las curvas de solución definidas por la Ecuación\ ref {eq:2.2.8} son semicírculos por encima del\(x\) eje -y las definidas por la Ecuación\ ref {eq:2.2.9} son semicírculos debajo del\(x\) eje -( Figura 2.2.1 ).
Solución b
La solución de la Ecuación\ ref {eq:2.2.5} es positiva cuando\(x=1\); de ahí, es de la forma Ecuación\ ref {eq:2.2.8}. Sustituyendo\(x=1\) y\(y=1\) en la Ecuación\ ref {eq:2.2.7} para satisfacer los rendimientos de la condición inicial\(a^2=2\); por lo tanto, la solución de la Ecuación\ ref {eq:2.2.5} es
\[y=\sqrt{2-x^2}, \quad - \sqrt{2}< x < \sqrt{2}. \nonumber \]
Solución c
La solución de la Ecuación\ ref {eq:2.2.6} es negativa cuando\(x=1\) y por lo tanto es de la forma Ecuación\ ref {eq:2.2.9}. Sustituyendo\(x=1\) y\(y=-2\) en Ecuación\ ref {eq:2.2.7} para satisfacer los rendimientos de condición inicial\(a^2=5\). De ahí que la solución de la Ecuación\ ref {eq:2.2.6} es
\[y=- \sqrt{5-x^2}, \quad -\sqrt{5} < x < \sqrt{5}. \nonumber \]
Soluciones Implícitas de Ecuaciones Separables
En Ejemplos 2.2.1 y 2.2.2 pudimos resolver la ecuación\(H(y)=G(x)+c\) para obtener fórmulas explícitas para soluciones de las ecuaciones diferenciales separables dadas. Como veremos en el siguiente ejemplo, esto no siempre es posible. En esta situación debemos ampliar nuestra definición de una solución de una ecuación separable. El siguiente teorema proporciona las bases para esta modificación. Omitimos la prueba, que requiere un resultado del cálculo avanzado llamado como teorema de la función implícita.
Supongamos que\(g=g(x)\) es continuo en\((a,b)\) y\(h=h(y)\) son continuos en\((c,d).\) Let\(G\) be an antiderivative of\(g\) on\((a,b)\) y let\(H\) be an antiderivative of\(h\) on\((c,d).\) Let\(x_0\) be an arbitrario point in\((a,b),\) let\(y_0\) be a punto en\((c,d)\) tal que\(h(y_0)\ne0,\) y definir
\[\label{eq:2.2.10} c=H(y_0)-G(x_0).\]
Luego hay una función\(y=y(x)\) definida en algún intervalo abierto\((a_1,b_1),\) donde\(a\le a_1<x_0<b_1\le b,\) tal que\(y(x_0)=y_0\) y
\[\label{eq:2.2.11} H(y)=G(x)+c\]
para\(a_1<x<b_1\). Por lo tanto,\(y\) es una solución del problema de valor inicial
\[\label{eq:2.2.12} h(y)y'=g(x),\quad y(x_0)=y_0.\]
Es conveniente decir que la Ecuación\ ref {eq:2.2.11} con\(c\) arbitraria es una solución implícita de\(h(y)y'=g(x)\). Las curvas definidas por la ecuación\ ref {eq:2.2.11} son curvas integrales de\(h(y)y'=g(x)\). Si\(c\) satisface la Ecuación\ ref {eq:2.2.10}, diremos que la Ecuación\ ref {eq:2.2.11} es una solución implícita del problema del valor inicial Ecuación\ ref {eq:2.2.12}. Sin embargo, tenga en cuenta estos puntos:
- Para algunas opciones de no puede\(c\) haber ninguna función diferenciable\(y\) que satisfaga la Ecuación\ ref {eq:2.2.11}.
- La función\(y\) en la ecuación\ ref {eq:2.2.11} (no la ecuación\ ref {eq:2.2.11} en sí misma) es una solución de\(h(y)y'=g(x)\).
- Encuentra soluciones implícitas de\[\label{eq:2.2.13} y'={2x+1\over5y^4+1}.\]
- Encuentre una solución implícita de\[\label{eq:2.2.14} y'={2x+1\over5y^4+1},\quad y(2)=1.\]
Solución a
Separación de rendimientos de variables
\[(5y^4+1)y'=2x+1. \nonumber \]
La integración produce la solución implícita
\[\label{eq:2.2.15} y^5+y=x^2+x+ c. \]
de Ecuación\ ref {eq:2.2.13}.
Solución b
Imponer la condición inicial\(y(2)=1\) en la Ecuación\ ref {eq:2.2.15} rinde\(1+1=4+2+c\), así\(c=-4\). Por lo tanto
\[y^5+y=x^2+x-4 \nonumber \]
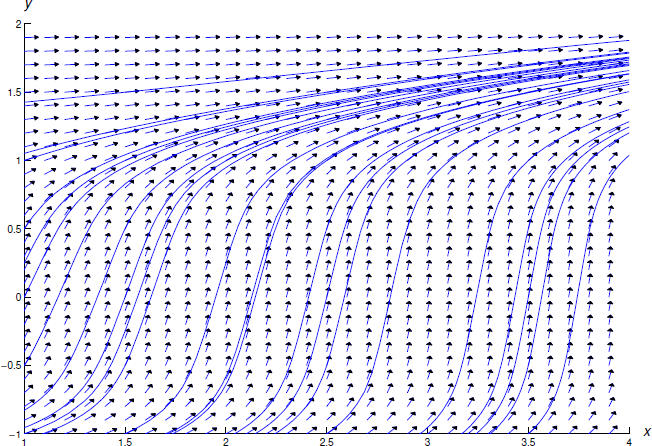
es una solución implícita del problema del valor inicial Ecuación\ ref {eq:2.2.14}. Aunque más de una función diferenciable\(y=y(x)\) satisface la Ecuación\ ref {eq:2.2.13} cerca\(x=1\), se puede demostrar que sólo existe una función de este tipo que satisface la condición inicial\(y(1)=2\). La Figura 2.2.2 muestra un campo de dirección y algunas curvas integrales para la Ecuación\ ref {eq:2.2.13}.
Soluciones Constantes de Ecuaciones Separables
Una ecuación de la forma
\[y'=g(x)p(y) \nonumber \]
es separable, ya que se puede reescribir como
\[{1\over p(y)}y'=g(x). \nonumber \]
No obstante, la división por no\(p(y)\) es legítima si\(p(y)=0\) por algunos valores de\(y\). Los siguientes dos ejemplos muestran cómo lidiar con este problema.
Encuentra todas las soluciones de
\[\label{eq:2.2.16} y'=2xy^2.\]
Solución
Aquí debemos dividirnos por\(p(y)=y^2\) para separar las variables. Esto no es legítimo si\(y\) es una solución de Ecuación\ ref {eq:2.2.16} que equivale a cero para algún valor de\(x\). Una de esas soluciones se puede encontrar por inspección:\(y \equiv 0\). Ahora supongamos que\(y\) es una solución de la Ecuación\ ref {eq:2.2.16} que no es idénticamente cero. Dado que\(y\) es continuo debe haber un intervalo en el que nunca\(y\) sea cero. Dado que la división por\(y^2\) es legítima para\(x\) en este intervalo, podemos separar variables en la Ecuación\ ref {eq:2.2.16} para obtener
\[{y'\over y^2}=2x. \nonumber \]
Integrando estos rendimientos
\[-{1\over y}=x^2+c, \nonumber \]
que es equivalente a
\[\label{eq:2.2.17} y=-{1\over x^2+c}.\]
Ahora hemos demostrado que si\(y\) es una solución de la Ecuación\ ref {eq:2.2.16} que no es idénticamente cero, entonces\(y\) debe ser de la forma Ecuación\ ref {eq:2.2.17}. Al sustituir la Ecuación\ ref {eq:2.2.17} en la Ecuación\ ref {eq:2.2.16}, puede verificar que la Ecuación\ ref {eq:2.2.17} es una solución de la Ecuación\ ref {eq:2.2.16}. Así, las soluciones de la Ecuación\ ref {eq:2.2.16} son\(y\equiv0\) y las funciones de la forma Ecuación\ ref {eq:2.2.17}. Tenga en cuenta que la solución\(y\equiv0\) no es de la forma Ecuación\ ref {eq:2.2.17} para ningún valor de\(c\).
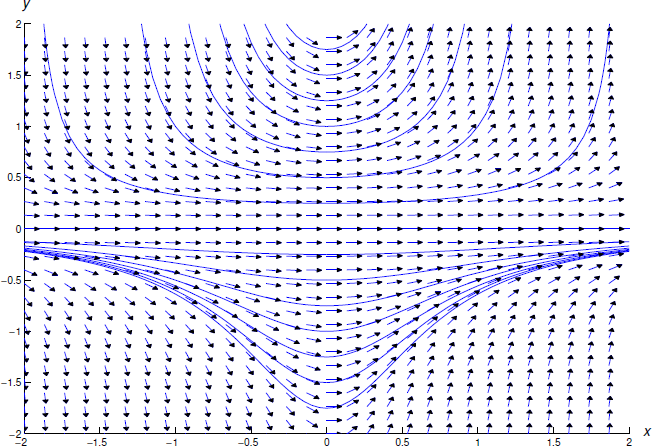
La figura 2.2.3 muestra un campo de dirección y algunas curvas integrales para la ecuación\ ref {eq:2.2.16}
Encuentra todas las soluciones de
\[\label{eq:2.2.18} y'={1\over2}x(1-y^2). \]
Aquí debemos dividirnos por\(p(y)=1-y^2\) para separar las variables. Esto no es legítimo si\(y\) es una solución de Ecuación\ ref {eq:2.2.18} que es igual\(\pm1\) para algún valor de\(x\). Dos soluciones de este tipo se pueden encontrar por inspección:\(y \equiv 1\) y\(y\equiv-1\). Ahora supongamos que\(y\) es una solución de la Ecuación\ ref {eq:2.2.18} tal que\(1-y^2\) no es idénticamente cero. Dado que\(1-y^2\) es continuo debe haber un intervalo en el que nunca\(1-y^2\) sea cero. Dado que la división por\(1-y^2\) es legítima para\(x\) en este intervalo, podemos separar variables en la Ecuación\ ref {eq:2.2.18} para obtener
\[{2y'\over y^2-1}=-x. \nonumber \]
Una expansión parcial de la fracción a la izquierda rinde
\[\left[{1\over y-1}-{1\over y+1}\right]y'=-x, \nonumber \]
e integrando rendimientos
\[\ln\left|{y-1\over y+1}\right|=-{x^2\over2}+k; \nonumber \]
por lo tanto,
\[\left|{y-1\over y+1}\right|=e^ke^{-x^2/2}. \nonumber \]
Ya que\(y(x)\ne\pm1\) para\(x\) en el intervalo en discusión, la cantidad\((y-1)/(y+1)\) no puede cambiar signo en este intervalo. Por lo tanto podemos reescribir la última ecuación como
\[{y-1\over y+1}=ce^{-x^2/2}, \nonumber \]
donde\(c=\pm e^k\), dependiendo del signo de\((y-1)/(y+1)\) en el intervalo. Resolviendo\(y\) rendimientos
\[\label{eq:2.2.19} y={1+ce^{-x^2/2}\over 1-ce^{-x^2/2}}. \]
Ahora hemos demostrado que si\(y\) es una solución de la Ecuación\ ref {eq:2.2.18} que no es idéntica a\(\pm1\), entonces\(y\) debe ser como en la Ecuación\ ref {eq:2.2.19}. Al sustituir la Ecuación\ ref {eq:2.2.19} en la Ecuación\ ref {eq:2.2.18} se puede verificar que la Ecuación\ ref {eq:2.2.19} es una solución de la Ecuación\ ref {eq:2.2.18}. Así, las soluciones de la Ecuación\ ref {eq:2.2.18} son\(y\equiv1\),\(y\equiv-1\) y las funciones de la forma Ecuación\ ref {eq:2.2.19}. Obsérvese que la solución constante se\(y \equiv 1\) puede obtener de esta fórmula tomando\(c=0\); sin embargo, la otra solución constante,\(y \equiv -1\), no se puede obtener de esta manera.
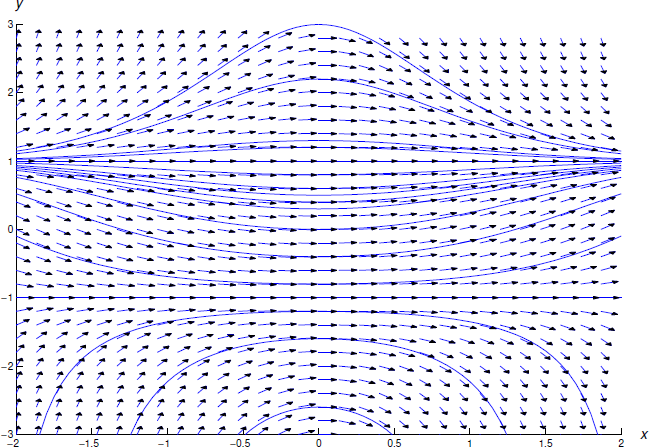
La figura 2.2.4 muestra un campo de dirección y algunas integrales para la ecuación\ ref {eq:2.2.18}.
Diferencias entre ecuaciones lineales y no lineales
Teorema 2.1.2 establece que si\(p\) y\(f\) son continuos en\((a,b)\) entonces cada solución de
\[y'+p(x)y=f(x) \nonumber \]
on se\((a,b)\) puede obtener eligiendo un valor para la constante\(c\) en la solución general, y si\(x_0\) hay algún punto en\((a,b)\) y\(y_0\) es arbitrario, entonces el problema del valor inicial
\[y'+p(x)y=f(x),\quad y(x_0)=y_0 \nonumber \]
tiene una solución en\((a,b)\).
Lo no es cierto para las ecuaciones no lineales. Primero, vimos en Ejemplos 2.2.4 y 2.2.5 que una ecuación no lineal puede tener soluciones que no se pueden obtener eligiendo un valor específico de una constante que aparece en una familia de soluciones de un parámetro. Segundo, en general es imposible determinar el intervalo de validez de una solución a un problema de valor inicial para una ecuación no lineal simplemente examinando la ecuación, ya que el intervalo de validez puede depender de la condición inicial. Por ejemplo, en Example 2.2.2 vimos que la solución de
\[{dy\over dx}=-{x\over y},\quad y(x_0)=y_0 \nonumber \]
es válido el\((-a,a)\), donde\(a=\sqrt{x_0^2+y_0^2}\).
Resolver el problema de valor inicial
\[y'=2xy^2, \quad y(0)=y_0 \nonumber \]
y determinar el intervalo de validez de la solución.
Solución
Primero supongamos\(y_0\ne0\). De Example 2.2.4 , sabemos que\(y\) debe ser de la forma
\[\label{eq:2.2.20} y=-{1\over x^2+c}.\]
Imponer la condición inicial lo demuestra\(c=-1/y_0\). Sustituyendo esto en la ecuación\ ref {eq:2.2.20} y reordenando los términos produce la solución
\[y= {y_0\over 1-y_0x^2}. \nonumber \]
Esta es también la solución si\(y_0=0\). Si\(y_0<0\), el denominador no es cero para ningún valor de\(x\), entonces la solución es válida en\((-\infty,\infty)\). Si\(y_0>0\), la solución es válida sólo el\((-1/\sqrt{y_0},1/\sqrt{y_0})\).


