2.6: Factores integradores
- Page ID
- 115171
En la Sección 2.5 vimos que si\(M\),\(N\),\(M_y\) y\(N_x\) son continuos y\(M_y=N_x\) en un rectángulo abierto\(R\) entonces
\[\label{eq:2.6.1} M(x,y)\,dx+N(x,y)\,dy=0\]
es exacto en\(R\). A veces una ecuación que no es exacta puede hacerse exacta multiplicándola por una función apropiada. Por ejemplo,
\[\label{eq:2.6.2} (3x+2y^2)\,dx+2xy\,dy=0\]
no es exacto, ya que\(M_y(x,y)=4y\ne N_x(x,y)=2y\) en la Ecuación\ ref {eq:2.6.2}. Sin embargo, multiplicando la ecuación\ ref {eq:2.6.2} por\(x\) rendimientos
\[\label{eq:2.6.3} (3x^2+2xy^2)\,dx+2x^2y\,dy=0,\]
lo cual es exacto, ya que\(M_y(x,y)=N_x(x,y)=4xy\) en la Ecuación\ ref {eq:2.6.3}. Resolviendo la ecuación\ ref {eq:2.6.3} mediante el procedimiento dado en la Sección 2.5 produce la solución implícita
\[x^3+x^2y^2=c.\nonumber \]
Una función\(\mu=\mu(x,y)\) es un factor de integración para la Ecuación\ ref {eq:2.6.1} si\[\label{eq:2.6.4} \mu(x,y)M (x,y)\,dx+\mu(x,y)N (x,y)\,dy=0\] es exacta. Si conocemos un factor integrador\(\mu\) para la Ecuación\ ref {eq:2.6.1}, podemos resolver la ecuación exacta Ecuación\ ref {eq:2.6.4} por el método de la Sección 2.5. Sería bueno que pudiéramos decir que la Ecuación\ ref {eq:2.6.1} y la Ecuación\ ref {eq:2.6.4} siempre tienen las mismas soluciones, pero esto no es así. Por ejemplo, una solución\(y=y(x)\) de Ecuación\ ref {eq:2.6.4} tal que\(\mu(x,y(x))=0\) en algún intervalo\(a<x<b\) podría no ser una solución de\ ref {eq:2.6.1} (Ejercicio 2.6.1)
Encontrar factores integradores
Al aplicar el Teorema 2.5.2 (con\(M\) y\(N\) reemplazado por\(\mu M\) y\(\mu N\)), vemos que la Ecuación\ ref {eq:2.6.4} es exacta en un rectángulo abierto\(R\) si\(\mu M\),\(\mu N\),\((\mu M)_y\), y\((\mu N)_x\) son continuas y\[{\partial\over\partial y}(\mu M)={\partial\over\partial x} (\mu N) \quad \text{or, equivalently,} \quad \mu_yM+\mu M_y=\mu_xN+\mu N_x\nonumber \] continuas\(R\). Es mejor reescribir la última ecuación como la\[\label{eq:2.6.5} \mu(M_y-N_x)=\mu_xN-\mu_yM,\] cual se reduce al resultado conocido para ecuaciones exactas; es decir, si\(M_y=N_x\) entonces la Ecuación\ ref {eq:2.6.5} se mantiene con\(\mu=1\), entonces la Ecuación\ ref {eq:2.6.1} es exacta.
Puede pensar que la Ecuación\ ref {eq:2.6.5} es de poco valor, ya que involucra derivadas parciales del factor integrador desconocido\(\mu\), y no hemos estudiado métodos para resolver tales ecuaciones. Sin embargo, ahora mostraremos que la Ecuación\ ref {eq:2.6.5} es útil si restringimos nuestra búsqueda a factores de integración que son productos de una función de\(x\) y una función de\(y\); es decir,\(\mu(x,y)=P(x)Q(y)\). No estamos diciendo que cada ecuación\(M\,dx+N\,dy=0\) tenga un factor integrador de esta forma; más bien, estamos diciendo que algunas ecuaciones tienen tales factores integradores.Ahora desarrollaremos una manera de determinar si una ecuación dada tiene tal factor de integración, y un método para encontrar el factor integrador en este caso.
Si\(\mu(x,y)=P(x)Q(y)\), entonces\(\mu_x(x,y)=P'(x)Q(y)\) y\(\mu_y(x,y)=P(x)Q'(y)\), entonces la ecuación\ ref {eq:2.6.5} se convierte
\[\label{eq:2.6.6} P(x)Q(y)(M_y-N_x)=P'(x)Q(y)N-P(x)Q'(y)M,\]o, después de dividirlo por\(P(x)Q(y)\),
\[\label{eq:2.6.7} M_y-N_x={P'(x)\over P(x)}N-{Q'(y)\over Q(y)}M.\]Ahora vamos\[p(x)={P'(x)\over P(x)} \quad \text{and} \quad q(y)={Q'(y)\over Q(y)},\nonumber \] así Ecuación\ ref {eq:2.6.7} se convierte
\[\label{eq:2.6.8} M_y-N_x=p(x)N-q(y)M.\]
Obtuvimos la Ecuación\ ref {eq:2.6.8} asumiendo que\(M\,dx+N\,dy=0\) tiene un factor integrador\(\mu(x,y)=P(x)Q(y)\). Sin embargo, ahora podemos ver la Ecuación\ ref {eq:2.6.7} de manera diferente: Si hay funciones\(p=p(x)\) y\(q=q(y)\) que satisfacen la Ecuación\ ref {eq:2.6.8} y definimos
\[\label{eq:2.6.9} P(x)=\pm e^{\int p(x)\,dx}\quad \text{and} \quad Q(y)=\pm e^{\int q(y)\,dy},\]
luego invertir los pasos que llevaron de la Ecuación\ ref {eq:2.6.6} a la Ecuación\ ref {eq:2.6.8} muestra que\(\mu(x,y)=P(x)Q(y)\) es un factor integrador para\(M\,dx+N\,dy=0\). Al usar este resultado, tomamos las constantes de integración en la Ecuación\ ref {eq:2.6.9} para que sean cero y elegimos los signos convenientemente para que el factor integrador tenga la forma más simple.
No existe un método general simple para determinar si existen funciones\(p=p(x)\) y la ecuación\(q=q(y)\) satisfactoria\ ref {eq:2.6.8}. Sin embargo, el siguiente teorema da condiciones simples suficientes para que la ecuación dada tenga un factor integrador que dependa solo de una de las variables independientes\(x\) y\(y\), y para encontrar un factor integrador en este caso.
Dejar\(M,\)\(N,\)\(M_y,\) y\(N_x\) ser continuo sobre un rectángulo abierto\(R.\) Luego:
(a) Si\((M_y-N_x)/N\) es independiente de\(y\) on\(R\) y definimos\[p(x)={M_y-N_x\over N}\nonumber \] entonces\[\label{eq:2.6.10} \mu(x)=\pm e^{\int p(x)\,dx}\] es un factor integrador para\[\label{eq:2.6.11} M(x,y)\,dx+N(x,y)\,dy=0\] on\(R.\)
(b) Si\((N_x-M_y)/M\) es independiente de\(x\) on\(R\) y definimos\[q(y)={N_x-M_y\over M},\nonumber \] entonces\[\label{eq:2.6.12} \mu(y)=\pm e^{\int q(y)\,dy}\] es un factor integrador para la Ecuación\ ref {eq:2.6.11} on\(R.\)
- Prueba
-
(a) Si\((M_y-N_x)/N\) es independiente de\(y\), entonces la Ecuación\ ref {eq:2.6.8} se mantiene con\(p=(M_y-N_x)/N\) y\(q\equiv0\). Por\[P(x)=\pm e^{\int p(x)\,dx}\quad\text{ and}\quad Q(y)=\pm e^{\int q(y)\,dy}=\pm e^0=\pm1,\nonumber \] lo tanto, la Ecuación\ ref {eq:2.6.10} es un factor integrador para la Ecuación\ ref {eq:2.6.11} on\(R\).
(b) Si\((N_x-M_y)/M\) es independiente de\(x\) entonces eqref eq:2.6.8 se mantiene con y\(p\equiv0\),\(q=(N_x-M_y)/M\) y un argumento similar muestra que la Ecuación\ ref {eq:2.6.12} es un factor de integración para la Ecuación\ ref {eq:2.6.11} on.\(R\)
Los siguientes dos ejemplos muestran cómo aplicar el Teorema 2.6.1 .
Encuentra un factor integrador para la ecuación\[\label{eq:2.6.13} (2xy^3-2x^3y^3-4xy^2+2x)\,dx+(3x^2y^2+4y)\,dy=0\] y resuelve la ecuación.
Solución
En la Ecuación\ ref {eq:2.6.13}\[M=2xy^3-2x^3y^3-4xy^2+2x,\ N=3x^2y^2+4y,\nonumber \] y\[M_y-N_x=(6xy^2-6x^3y^2-8xy)-6xy^2=-6x^3y^2-8xy,\nonumber \] así la Ecuación\ ref {eq:2.6.13} no es exacta. Sin embargo,\[{M_y-N_x\over N}=-{6x^3y^2+8xy\over 3x^2y^2+4y}=-2x\nonumber \] es independiente de\(y\), por lo que el Teorema 2.6.1 (a) se aplica con\(p(x)=-2x\). Ya que\[\int p (x)\,dx=-\int 2x\,dx=-x^2,\nonumber \]\(\mu(x)=e^{-x^2}\) es un factor integrador. Al multiplicar la ecuación\ ref {eq:2.6.13} por se\(\mu\) obtiene la ecuación exacta\[\label{eq:2.6.14} e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\,dx+ e^{-x^2}(3x^2y^2+4y)\,dy=0.\]
Para resolver esta ecuación, debemos encontrar una función\(F\) tal que\[\label{eq:2.6.15} F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\] e\[\label{eq:2.6.16} F_y(x,y)=e^{-x^2}(3x^2y^2+4y).\] Integrando Ecuación\ ref {eq:2.6.16} con respecto a\(y\) rendimientos\[\label{eq:2.6.17} F(x,y)=e^{-x^2}(x^2y^3+2y^2)+\psi(x).\] Diferenciando esto con respecto a\(x\) rendimientos\[F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2)+\psi'(x).\nonumber \] Comparando esto con la Ecuación\ ref {eq:2.6.15} demuestra que \(\psi'(x)= 2xe^{-x^2}\); por lo tanto, podemos dejar\(\psi(x)=-e^{-x^2}\) entrar la Ecuación\ ref {eq:2.6.17} y concluir que\[e^{-x^2}\left(y^2(x^2y+2)-1\right)=c\nonumber \] es una solución implícita de la Ecuación\ ref {eq:2.6.14}. También es una solución implícita de la Ecuación\ ref {eq:2.6.13}.
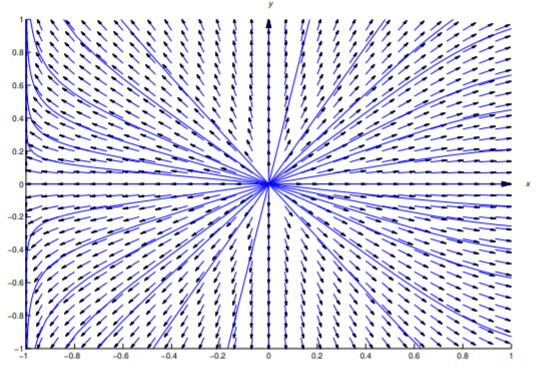
La figura 2.6.1 muestra un campo de dirección y algunas curvas integrales para la ecuación\ ref {eq:2.6.13}
Encuentre un factor de integración para
\[\label{eq:2.6.30} 2xy^{3}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)dy=0\]
y resolver la ecuación.
Solución
En Ecuación\ ref {eq:2.6.30},
\[M=2xy^{3},\quad N=3x^{2}y^{2}+x^{2}y^{3}+1,\nonumber \]
y
\[M_{y}-N_{x}=6x^{2}-(6xy^{2}+2xy^{3})=-2xy^{3},\nonumber \]
así que la ecuación\ ref {eq:2.6.30} no es exacta. Por otra parte,
\[\frac{M_y-N_x}{N}=-\frac{2xy^3}{3x^2y^2+x^2y^2+1}\nonumber \]
no es independiente de\(y\), por lo que el Teorema 2.6.1 (a) no aplica. Sin embargo, el Teorema 2.6.1 (b) sí aplica, ya que
\[\frac{N_x-M_y}{M}=\frac{2xy^3}{2xy^3}=1\nonumber \]
no es independiente de\(x\), así que podemos tomar\(q(y)=1\). Desde
\[\int q(y)dy=\int dy=y,\nonumber \]
\(\mu (y)=e^{y}\)es un factor integrador. Al multiplicar la ecuación\ ref {eq:2.6.30} por se\(\mu\) obtiene la ecuación exacta.
\[\label{eq:2.6.36} 2xy^{3}e^{y}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}dy=0.\]
Para resolver esta ecuación, debemos encontrar una función\(F\) tal que
\[\label{eq:2.6.37} F_x (x,y)=2xy^{3}e^{y}\]
y
\[\label{eq:2.6.38} F_{y}(x,y)=(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}.\]
Ecuación integradora\ ref {eq:2.6.37} con respecto a\(x\) rendimientos
\[\label{eq:2.6.39} F (x,y)=x^{2} y^{3} e^{y} + \phi (y)\]
Diferenciando esto con respecto a\(y\) los rendimientos
\[F_{y}= (3x^{2} y^{2} + x^{2} y^{3}) e^{y} + \phi ' (y)\nonumber \]
y comparando esto con la Ecuación\ ref {eq:2.6.38} muestra que φ 0 (y) = e y. Por lo tanto, establecemos φ (y) = e y en la Ecuación\ ref {eq:2.6.39} y concluimos que
\[(x^{2}y^{3}+1)e^{y}=c\nonumber \]
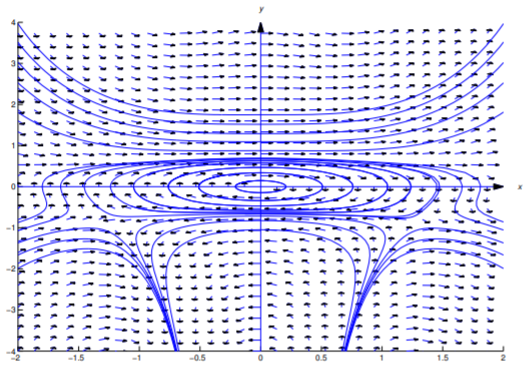
es una solución implícita de\ ref {eq:2.6.36}. También es una solución implícita de\ ref {eq:2.6.30}. La figura 2.6.2 muestra un campo de dirección y algunas curvas integrales para\ ref {eq:2.6.30}.
El teorema 2.6.1 no se aplica en el siguiente ejemplo, pero el argumento más general que llevó al Teorema 2.6.1 proporciona un factor integrador.
Encuentre un factor de integración para
\[\label{eq:2.6.42} (3xy+6y^{2})dx+(2x^{2} +9xy)dy=0\]
y resolver la ecuación.
Solución
En Ecuación\ ref {eq:2.6.42}
\[M=3xy+6y^2, \quad N=2x^2+9xy,\nonumber \]
y
\[M_y -N_x =(3x+12y)-(4x+9y)=-x+3y.\nonumber \]
Por lo tanto
\[\frac{M_y - N_x}{M}=\frac{-x+3y}{3xy+6y^2}\quad\text{and}\quad\frac{N_x - M_y}{N}=\frac{x-3y}{2x^2 +9xy}\nonumber \]
por lo que el teorema 2.6.1 no aplica. Siguiendo el argumento más general que llevó al Teorema 2.6.1 , buscamos funciones\(p = p(x)\) y\(q = q(y)\) tal que
\[M_y - N_x = p(x)N-q(y)M;\nonumber \]
es decir,
\[-x+3y=p(x)(2x^2+9xy)-q(y)(3xy+6y^2).\nonumber \]
Dado que el lado izquierdo contiene solo términos de primer grado en\(x\) y\(y\), reescribimos esta ecuación como
\[xp(x)(2x+9y)-yq(y)(3x+6y)=-x+3y.\nonumber \]
Esta será una identidad si
\[\label{eq:2.6.49} xp(x)=A\quad\text{and}yq(y)=B,\]
donde\(A\) y\(B\) son constantes tales que
\[-x+3y=A(2x+9y)-B(3x+6y),\nonumber \]
o, equivalentemente,
\[-x+3y=(2A-3B)x+(9A-6B)y.\nonumber \]
Equiparar los coeficientes de x e y en ambos lados muestra que la última ecuación se mantiene para todos\((x, y)\) si
\[\begin{aligned} 2A-3B &=-1 \\ 9A-6B &=3 \end{aligned}\nonumber \]
que tiene la solución A = 1, B = 1. Por lo tanto, la ecuación\ ref {eq:2.6.49} implica que
\[p(x)=\frac{1}{x}\quad\text{and}\quad q(y)=\frac{1}{y}.\nonumber \]
Desde
\[\int p(x)dx=\ln |x|\quad\text{and}\quad\int q(y)dy=\ln |y|,\nonumber \]
podemos dejar\(P(x) = x\) y\(Q(y) = y\); de ahí,\(µ(x, y) = xy\) es un factor integrador. Al multiplicar la ecuación\ ref {eq:2.6.42} por se\(µ\) obtiene la ecuación exacta
\[(3x^{2}y^{2}+6xy^{3})dx + (2x^{3}y+9x^{2}y^{2})dy=0.\nonumber \]
Te dejamos usar el método de la Sección 2.5 para demostrar que esta ecuación tiene la solución implícita
\[\label{eq:2.6.55} x^{3}y^{2}+3x^{2}y^{3}=c.\]
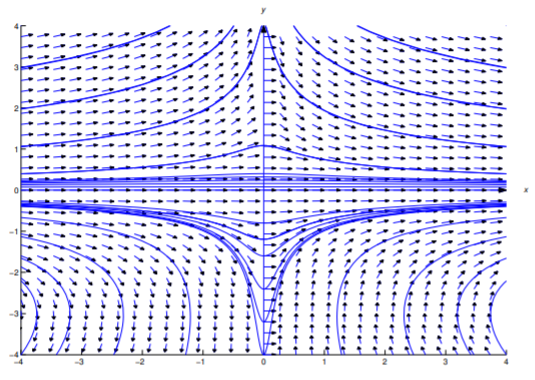
Esta es también una solución implícita de la Ecuación\ ref {eq:2.6.42}. Ya que x ≡ 0 e y ≡ 0 satisfacen la Ecuación\ ref {eq:2.6.55}, deberías verificar para ver que x ≡ 0 e y ≡ 0 son también soluciones de Ecuación\ ref {eq:2.6.42}. (¿Por qué es necesario verificar esto?) La Figura 2.6.3 muestra un campo de dirección y curvas integrales para la Ecuación\ ref {eq:2.6.42}. Consulte el Ejercicio 2.6.28 para una discusión general de ecuaciones como Ecuación\ ref {eq:2.6.42}.
La ecuación separable
\[\label{eq:2.6.56} -ydx+(x+x^{6})dy=0\]
se puede convertir a la ecuación exacta
\[\label{eq:2.6.57} -\frac{dx}{x+x^{6}}+\frac{dy}{y}=0\]
multiplicando por el factor integrador
\[\mu (x,y)=\frac{1}{y(x+x^{6})}.\nonumber \]
Sin embargo, para resolver la Ecuación\ ref {eq:2.6.57} por el método de la Sección 2.5 tendríamos que evaluar la desagradable integral
\[\int\frac{dx}{x+x^{6}}.\nonumber \]
En cambio, resolvemos la Ecuación\ ref {eq:2.6.56} explícitamente para\(y\) al encontrar un factor integrador de la forma\(µ(x, y) = x^{a}y^{b}\).
Solución
En Ecuación\ ref {eq:2.6.56}
\[M=-y,\ N=x+x^6,\nonumber \]
y
\[M_y-N_x=-1-(1+6x^5)=-2-6x^5.\nonumber \]
Buscamos funciones\(p=p(x)\) y\(q=q(y)\) tal que
\[M_y-N_x=p(x)N-q(y)M;\nonumber \]
es decir,
\[\label{eq:2.6.28} -2-6x^5=p(x)(x+x^6)+q(y)y.\]
El lado derecho contendrá el término\(-6x^5\) si\(p(x)=-6/x\). Entonces la Ecuación\ ref {eq:2.6.28} se convierte en
\[-2-6x^5=-6-6x^5+q(y)y,\nonumber \]
así\(q(y)=4/y\). Desde
\[\int p(x)\,dx=-\int{6\over x}\,dx=-6\ln|x|=\ln{1\over x^6},\nonumber \]
y
\[\int q(y)\,dy=\int{4\over y}\,dy=4\ln |y|=\ln{y^4},\nonumber \]
podemos tomar\(P(x)=x^{-6}\) y\(Q(y)=y^4\), que arroja el factor integrador\(\mu(x,y)=x^{-6}y^4\). Al multiplicar la ecuación\ ref {eq:2.6.56} por se\(\mu\) obtiene la ecuación exacta
\[-{y^5\over x^6}\,dx+\left({y^4\over x^5}+y^4\right) \,dy=0.\nonumber \]
Te dejamos usar el método de la Sección 2.5 para demostrar que esta ecuación tiene la solución implícita
\[\left({y\over x}\right)^5+y^5=k.\nonumber \]
Resolviendo\(y\) rendimientos
\[y=k^{1/5}x(1+x^5)^{-1/5},\nonumber \]
que reescribimos como
\[y=cx(1+x^5)^{-1/5}\nonumber \]
renombrando la constante arbitraria. Esta es también una solución de la Ecuación\ ref {eq:2.6.56}.
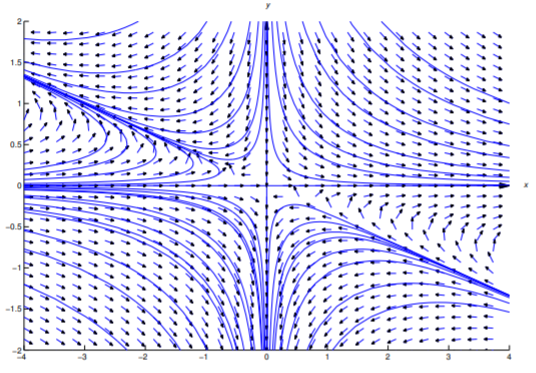
La Figura 2.6.4 muestra un campo de dirección y algunas curvas integrales para la Ecuación\ ref {eq:2.6.56}.