5.2: Ecuaciones homogéneas de coeficiente constante

Última actualización
Guardar como PDF

Page ID: 114918

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Esta sección trata de ecuaciones homogéneas de la forma especial $$ ay"+por'+cy=0, $$ donde$a$,$b$, y$c$ son constantes ($a\ne0$). Cuando hayas completado esta sección sabrás todo lo que hay que saber para resolver este tipo de ecuaciones.

Si$a,b$, y$c$ son constantes reales y$a\ne0$, entonces

\[ay''+by'+cy=F(x)\nonumber \]

se dice que es una ecuación de coeficiente constante. En esta sección consideramos la ecuación del coeficiente constante homogéneo

\[\label{eq:5.2.1} ay''+by'+cy=0.\]

Como veremos, todas las soluciones de Ecuación\ ref {eq:5.2.1} se definen en$(-\infty,\infty)$. Siendo este el caso, omitiremos referencias al intervalo en el que se definen las soluciones, o en el que un conjunto dado de soluciones es un conjunto fundamental, etc., ya que el intervalo siempre lo será$(-\infty,\infty)$.

La clave para resolver la Ecuación\ ref {eq:5.2.1} es que si$y=e^{rx}$ donde$r$ es una constante entonces el lado izquierdo de la Ecuación\ ref {eq:5.2.1} es un múltiplo de$e^{rx}$; así, si$y=e^{rx}$ entonces$y'=re^{rx}$ y$y''=r^2e^{rx}$, así

\[\label{eq:5.2.2} ay''+by'+cy=ar^2e^{rx}+bre^{rx}+ce^{rx}=(ar^2+br+c)e^{rx}.\]

El polinomio cuadrático

\[p(r)=ar^2+br+c\nonumber \]

es el polinomio característico de la Ecuación\ ref {eq:5.2.1}, y$p(r)=0$ es la ecuación característica. De la Ecuación\ ref {eq:5.2.2} podemos ver que$y=e^{rx}$ es una solución de la Ecuación\ ref {eq:5.2.1} si y solo si$p(r)=0$.

Las raíces de la ecuación característica están dadas por la fórmula cuadrática

\[\label{eq:5.2.3} r={-b\pm\sqrt{b^2-4ac}\over2a}.\]

Considerar tres casos

Caso 1:$b^2-4ac>0$, por lo que la ecuación característica tiene dos raíces reales distintas.
Caso 2:$b^2-4ac=0$, por lo que la ecuación característica tiene una raíz real repetida.
Caso 3:$b^2-4ac<0$, por lo que la ecuación característica tiene raíces complejas.

En cada caso comenzaremos con un ejemplo.

Caso 1: Raíces Reales Distintivas

Ejemplo 5.2.1

Encuentre la solución general de\[\label{eq:5.2.4} y''+6y'+5y=0.\]
Resolver el problema de valor inicial\[\label{eq:5.2.5} y''+6y'+5y=0, \quad y(0)=3,\; y'(0)=-1.\]

Solución

a. El polinomio característico de la Ecuación\ ref {eq:5.2.4} es

\[p(r)=r^2+6r+5=(r+1)(r+5).\nonumber\]

Ya que$p(-1)=p(-5)=0$,$y_1=e^{-x}$ y$y_2=e^{-5x}$ son soluciones de Ecuación\ ref {eq:5.2.4}. Como no$y_2/y_1=e^{-4x}$ es constante, el Teorema 5.1.6 implica que la solución general de la Ecuación\ ref {eq:5.2.4} es

\[\label{eq:5.2.6} y=c_1e^{-x}+c_2e^{-5x}.\]

b. debemos determinar$c_1$ y$c_2$ en la Ecuación\ ref {eq:5.2.6} para que$y$ satisfaga las condiciones iniciales en la Ecuación\ ref {eq:5.2.5}. Ecuación diferenciadora\ ref {eq:5.2.6} rendimientos

\[\label{eq:5.2.7} y'=-c_1e^{-x}-5c_2e^{-5x}.\]

Imponer las condiciones iniciales$y(0)=3,\, y'(0)=-1$ en Ecuación\ ref {eq:5.2.6} y Ecuación\ ref {eq:5.2.7} rendimientos

\[\begin{array}{rcr} \phantom{-}c_1+\phantom{5}c_2 & = & 3\phantom{.}\\ -c_1-5c_2 & = & -1. \end{array}\nonumber \]

La solución de este sistema es$c_1=7/2,c_2=-1/2$. Por lo tanto, la solución de la Ecuación\ ref {eq:5.2.5} es

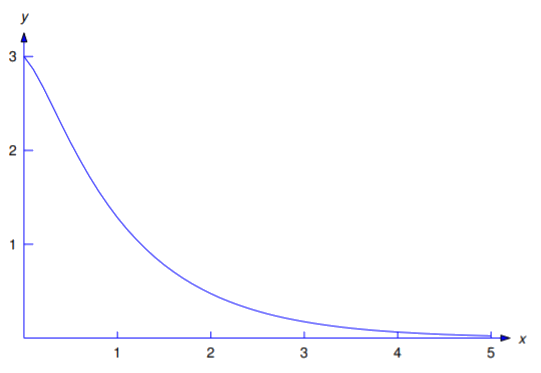
\[y={7\over2}e^{-x}-{1\over2}e^{-5x}.\nonumber \]

La figura 5.2.1 es una gráfica de esta solución.

Si la ecuación característica tiene raíces reales distintas arbitrarias$r_1$ y$r_2$, entonces$y_1=e^{r_1x}$ y$y_2=e^{r_2x}$ son soluciones de$ay''+by'+cy=0$. Dado que$y_2/y_1=e^{(r_2-r_1)x}$ es inconstante, el Teorema 5.1.6 implica que$\{y_1,y_2\}$ es un conjunto fundamental de soluciones de$ay''+by'+cy=0$.

Figura 5.2.1 :$y=\frac{7}{2}e^{-x}-\frac{1}{2}e^{-5x}$

Caso 2: Una raíz real repetida

Ejemplo 5.2.2

Encuentre la solución general de\[\label{eq:5.2.8} y''+6y'+9y=0.\]
Resolver el problema de valor inicial\[\label{eq:5.2.9} y''+6y'+9y=0, \quad y(0)=3,\; y'(0)=-1.\]

Solución

a. El polinomio característico de la Ecuación\ ref {eq:5.2.8} es

\[p(r)=r^2+6r+9=(r+3)^2,\nonumber \]

así que la ecuación característica tiene la raíz real repetida$r_1=-3$. Por lo tanto$y_1=e^{-3x}$ es una solución de la Ecuación\ ref {eq:5.2.8}. Dado que la ecuación característica no tiene otras raíces, la Ecuación\ ref {eq:5.2.8} no tiene otras soluciones de la forma$e^{rx}$. Buscamos soluciones de la forma$y=uy_1=ue^{-3x}$, donde$u$ hay una función que ahora determinaremos. (Esto debería recordarle el método de variación de los parámetros utilizados en la Sección 2.1 para resolver la ecuación no homogénea$y'+p(x)y=f(x)$, dada una solución$y_1$ de la ecuación complementaria$y'+p(x)y=0$. También es un caso especial de un método llamado reducción del orden que estudiaremos en la Sección 5.6. Para otras formas de obtener una segunda solución de la Ecuación\ ref {eq:5.2.8} que no es un múltiplo de$e^{-3x}$, ver Ejercicios 5.1.9, 5.1.12 y 5.1.33.

Si$y=ue^{-3x}$, entonces

\[y'=u'e^{-3x}-3ue^{-3x}\quad \text{and} \quad y''=u''e^{-3x}-6u'e^{-3x}+9ue^{-3x},\nonumber \]

por lo

\[\begin{aligned} y''+6y'+9y&=e^{-3x}\left[(u''-6u'+9u)+6(u'-3u)+9u\right]\\ &=e^{-3x}\left[u''-(6-6)u'+(9-18+9)u\right]=u''e^{-3x}.\end{aligned}\nonumber \]

Por lo tanto$y=ue^{-3x}$ es una solución de la Ecuación\ ref {eq:5.2.8} si y sólo si$u''=0$, que es equivalente a$u=c_1+c_2x$, donde$c_1$ y$c_2$ son constantes. Por lo tanto cualquier función de la forma

\[\label{eq:5.2.10} y=e^{-3x}(c_1+c_2x)\]

es una solución de la Ecuación\ ref {eq:5.2.8}. Dejando$c_1=1$ y$c_2=0$ rinde la solución$y_1=e^{-3x}$ que ya conocíamos. Dejar$c_1=0$ y$c_2=1$ producir la segunda solución$y_2=xe^{-3x}$. Dado que no$y_2/y_1=x$ es constante, el Teorema 5.1.6 implica que$\{y_1,y_2\}$ es un conjunto fundamental de soluciones de la Ecuación\ ref {eq:5.2.8}, y la Ecuación\ ref {eq:5.2.10} es la solución general.

b. Ecuación diferenciadora\ ref {eq:5.2.10} rendimientos

\[\label{eq:5.2.11} y'=-3e^{-3x}(c_1+c_2x)+c_2e^{-3x}.\]

Imponiendo las condiciones iniciales$y(0)=3,\, y'(0)=-1$ en la Ecuación\ ref {eq:5.2.10} y Ecuación\ ref {eq:5.2.11} rinde$c_1=3$ y$-3c_1+c_2=-1$, así$c_2=8$. Por lo tanto, la solución de la Ecuación\ ref {eq:5.2.9} es

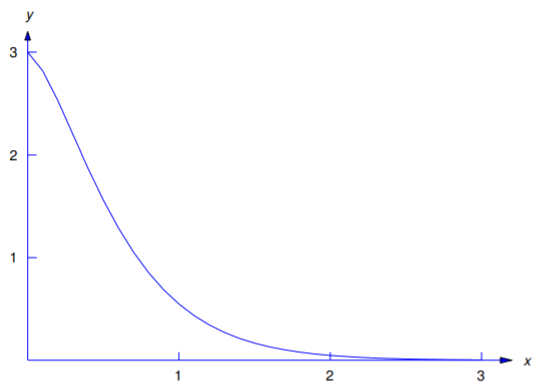
\[y=e^{-3x}(3+8x).\nonumber \]

La figura 5.2.2 es una gráfica de esta solución.

Si la ecuación característica de$ay''+by'+cy=0$ tiene una raíz repetida arbitraria$r_1$, el polinomio característico debe ser

\[p(r)=a(r-r_1)^2=a(r^2-2r_1r+r_1^2).\nonumber \]

Por lo tanto

\[ar^2+br+c=ar^2-(2ar_1)r+ar_1^2,\nonumber \]

lo que implica que$b=-2ar_1$ y$c=ar_1^2$. Por lo tanto se$ay''+by'+cy=0$ puede escribir como$a(y''-2r_1y'+r_1^2y)=0$. Dado que$a\ne0$ esta ecuación tiene las mismas soluciones que

\[\label{eq:5.2.12} y''-2r_1y'+r_1^2y=0.\]

Ya que$p(r_1)=0$, t$y_1=e^{r_1x}$ es una solución de$ay''+by'+cy=0$, y por lo tanto de la Ecuación\ ref {eq:5.2.12}. Procediendo como en el Ejemplo 5.2.1 , buscamos otras soluciones de Ecuación\ ref {eq:5.2.12} de la forma$y=ue^{r_1x}$; luego

\[y'=u'e^{r_1x}+rue^{r_1x}\quad \text{and} \quad y''=u''e^{r_1x}+2r_1u'e^{r_1x}+r_1^2ue^{r_1x},\nonumber \]

por lo

\[\begin{aligned} y''-2r_1y'+r_1^2y &=e^{rx}\left[(u''+2r_1u'+r_1^2u)- 2r_1(u'+r_1u)+r_1^2u\right]\\ &=e^{r_1x}\left[u''+(2r_1-2r_1)u'+(r_1^2-2r_1^2+r_1^2)u\right]=u''e^{r_1x}.\end{aligned}\]

Por lo tanto$y=ue^{r_1x}$ es una solución de la Ecuación\ ref {eq:5.2.12} si y sólo si$u''=0$, que es equivalente a$u=c_1+c_2x$, donde$c_1$ y$c_2$ son constantes. De ahí que cualquier función de la forma

\[\label{eq:5.2.13} y=e^{r_1x}(c_1+c_2x)\]

es una solución de la Ecuación\ ref {eq:5.2.12}. Dejar$c_1=1$ y$c_2=0$ aquí rinde la solución$y_1=e^{r_1x}$ que ya conocíamos. Dejar$c_1=0$ y$c_2=1$ producir la segunda solución$y_2=xe^{r_1x}$. Como no$y_2/y_1=x$ es constante, el Teorema 5.1.6 implica que$\{y_1,y_2\}$ es un conjunto fundamental de soluciones de la Ecuación\ ref {eq:5.2.12}, y la Ecuación\ ref {eq:5.2.13} es la solución general.

Caso 3: Raíces Conjugadas Complejas

Ejemplo 5.2.3

Encuentre la solución general de\[\label{eq:5.2.14} y''+4y'+13y=0.\]
Resolver el problema de valor inicial\[\label{eq:5.2.15} y''+4y'+13y=0, \quad y(0)=2,\; y'(0)=-3.\]

Solución

a. El polinomio característico de la Ecuación\ ref {eq:5.2.14} es

\[p(r)=r^2+4r+13=r^2+4r+4+9=(r+2)^2+9.\nonumber \]

Las raíces de la ecuación característica son$r_1=-2+3i$ y$r_2=-2-3i$. Por analogía con el Caso 1, es razonable esperar eso$e^{(-2+3i)x}$ y$e^{(-2-3i)x}$ son soluciones de la Ecuación\ ref {eq:5.2.14}. Esto es cierto (ver Ejercicio 5.2.34); sin embargo, aquí hay dificultades, ya que probablemente no estés familiarizado con las funciones exponenciales con argumentos complejos, y aunque lo estés, es inconveniente trabajar con ellas, ya que son complejo-valoradas. Tomaremos un enfoque más simple, que motivamos de la siguiente manera: la notación exponencial sugiere que

\[e^{(-2+3i)x}=e^{-2x}e^{3ix}\quad \text{and} \quad e^{(-2-3i)x}=e^{-2x}e^{-3ix},\nonumber \]

así que aunque no hayamos definido$e^{3ix}$ y$e^{-3ix}$, es razonable esperar que cada combinación lineal de$e^{(-2+3i)x}$ y$e^{(-2-3i)x}$ pueda escribirse como$y=ue^{-2x}$, donde$u$ depende de$x$. Para determinar$u$, observamos que si$y=ue^{-2x}$ entonces

\[y'=u'e^{-2x}-2ue^{-2x}\quad \text{and} \quad y''=u''e^{-2x}-4u'e^{-2x}+4ue^{-2x},\nonumber \]

por lo

\[\begin{aligned} y''+4y'+13y&=e^{-2x}\left[(u''-4u'+4u)+4(u'-2u)+13u\right]\\ &=e^{-2x}\left[u''-(4-4)u'+(4-8+13)u\right]=e^{-2x}(u''+9u).\end{aligned}\nonumber \]

Por lo tanto$y=ue^{-2x}$ es una solución de la Ecuación\ ref {eq:5.2.14} si y solo si

\[u''+9u=0.\nonumber \]

Del Ejemplo 5.1.2, la solución general de esta ecuación es

\[u=c_1\cos 3x +c_2\sin 3x. \nonumber \]

Por lo tanto cualquier función de la forma

\[\label{eq:5.2.16} y=e^{-2x}(c_1\cos 3x+c_2\sin 3x)\]

es una solución de la Ecuación\ ref {eq:5.2.14}. Dejando$c_1=1$ y$c_2=0$ rinde la solución$y_1=e^{-2x}\cos3x$. Dejar$c_1=0$ y$c_2=1$ producir la segunda solución$y_2=e^{-2x}\sin3x$. Como no$y_2/y_1=\tan3x$ es constante, el Teorema 5.1.6 implica que$\{y_1,y_2\}$ es un conjunto fundamental de soluciones de la Ecuación\ ref {eq:5.2.14}, y la Ecuación\ ref {eq:5.2.16} es la solución general.

b. Imponer la condición$y(0)=2$ en la Ecuación\ ref {eq:5.2.16} lo demuestra$c_1=2$. Ecuación diferenciadora\ ref {eq:5.2.16} rendimientos

\[y'=-2e^{-2x}(c_1\cos 3x+c_2\sin 3x) +3e^{-2x}(-c_1\sin 3x +c_2\cos 3x),\nonumber \]

e imponiendo la condición inicial$y'(0)=-3$ aquí rinde$-3=-2c_1+3c_2=-4+3c_2$, entonces$c_2=1/3$. Por lo tanto, la solución de la Ecuación\ ref {eq:5.2.15} es

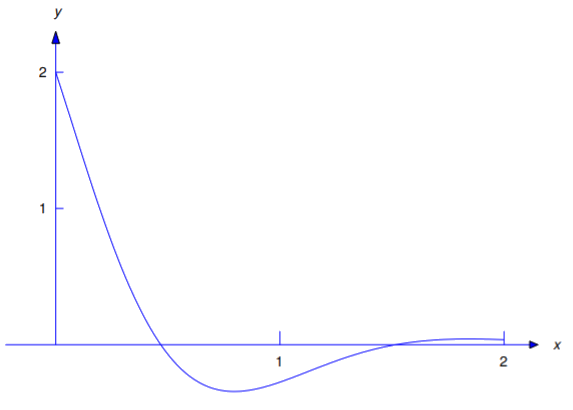
\[y=e^{-2x}(2\cos 3x+ {1\over3}\sin 3x).\nonumber \]

La Figura 5.2.3 es una gráfica de esta función.

Ahora supongamos que la ecuación característica de$ay''+by'+cy=0$ tiene raíces complejas arbitrarias; así,$b^2-4ac<0$ y, a partir de la ecuación\ ref {eq:5.2.3}, las raíces son

\[r_1 = {-b+i\sqrt{4ac-b^2}\over 2a},\quad r_2 = {-b-i\sqrt{4ac-b^2}\over 2a},\nonumber \]

que reescribimos como
\[\label{eq:5.2.17} r_1=\lambda+i \omega,\quad r_2 = \lambda - i \omega,\]

con

\[\lambda = -{b\over 2a},\quad \omega = {\sqrt{4ac-b^2}\over 2a}.\nonumber \]

No memorizar estas fórmulas. Solo recuerda eso$r_1$ y$r_2$ son de la forma Ecuación\ ref {eq:5.2.17}, donde$\lambda$ es un número real arbitrario y$\omega$ es positivo;$\lambda$ y$\omega$ son las partes real e imaginaria, respectivamente, de$r_1$. Del mismo modo,$\lambda$ y$-\omega$ son las partes reales e imaginarias de$r_2$. Decimos eso$r_1$ y$r_2$ son conjugados complejos,

Figura 5.2.3 :$y=e^{-2x}(2\cos 3x+\frac{1}{3}\sin 3x)$

lo que significa que tienen la misma parte real y sus partes imaginarias tienen los mismos valores absolutos, pero signos opuestos.

Como en Example 5.2.3 , es razonable esperar que las soluciones de$ay''+by'+cy=0$ sean combinaciones lineales de$e^{(\lambda+i\omega)x}$ y$e^{(\lambda-i\omega)x}$. Nuevamente, la notación exponencial sugiere que

\[e^{(\lambda+i\omega)x}=e^{\lambda x}e^{i\omega x}\quad \text{and} \quad e^{(\lambda-i\omega)x}=e^{\lambda x}e^{-i\omega x},\nonumber \]

así que aunque no hayamos definido$e^{i\omega x}$ y$e^{-i\omega x}$, es razonable esperar que cada combinación lineal de$e^{(\lambda+i\omega)x}$ y$e^{(\lambda-i\omega)x}$ pueda escribirse como$y=ue^{\lambda x}$, donde$u$ depende de$x$. Para determinar$u$ observamos primero que desde$r_1=\lambda+i\omega$ y$r_2=\lambda-i\omega$ son las raíces de la ecuación característica,$p$ deben ser de la forma

\[\begin{align*} p(r)&=a(r-r_1)(r-r_2)\\[4pt] &=a(r-\lambda-i\omega)(r-\lambda+i\omega) \\[4pt] &= a \left[(r-\lambda)^2+\omega^2\right] \\[4pt] &=a(r^2-2\lambda r +\lambda^2+\omega^2). \end{align*} \]

Por lo tanto se$ay''+by'+cy=0$ puede escribir como

\[a\left[y''-2\lambda y'+(\lambda^2+\omega^2)y\right]=0.\nonumber \]

Dado que$a\ne0$ esta ecuación tiene las mismas soluciones que

\[\label{eq:5.2.18} y''-2\lambda y'+(\lambda^2+\omega^2)y=0.\]

Para determinar$u$ observamos que si$y=ue^{\lambda x}$ entonces

\[y'=u'e^{\lambda x}+\lambda ue^{\lambda x}\quad \text{and} \quad y''=u''e^{\lambda x}+2\lambda u'e^{\lambda x}+\lambda^2ue^{\lambda x}.\nonumber \]

Sustituir estas expresiones en la ecuación\ ref {eq:5.2.18} y dejar caer los$e^{\lambda x}$ rendimientos del factor común

\[(u''+2\lambda u'+\lambda^2 u)-2\lambda(u'+\lambda u) +(\lambda^2+\omega^2)u=0,\nonumber \]

lo que simplifica

\[u''+\omega^2 u=0.\nonumber \]

Del Ejemplo 5.1.2, la solución general de esta ecuación es

\[u=c_1\cos\omega x +c_2\sin\omega x.\nonumber \]

Por lo tanto cualquier función de la forma

\[\label{eq:5.2.19} y=e^{\lambda x}(c_1\cos\omega x+c_2\sin\omega x)\]

es una solución de la Ecuación\ ref {eq:5.2.18}. Dejando$c_1=1$ y$c_2=0$ aquí rinde la solución$y_1=e^{\lambda x}\cos\omega x$. Dejar$c_1=0$ y$c_2=1$ producir una segunda solución$y_2=e^{\lambda x}\sin\omega x$. Ya que$y_2/y_1=\tan\omega x$ es inconstante, así Teorema 5.1.6 implica que$\{y_1,y_2\}$ es un conjunto fundamental de soluciones de la Ecuación\ ref {eq:5.2.18}, y la Ecuación\ ref {eq:5.2.19} es la solución general.

Resumen

El siguiente teorema resume los resultados de esta sección.

Teorema 5.2.1

$p(r)=ar^2+br+c$Sea el polinomio característico de

\[\label{eq:5.2.20} ay''+by'+cy=0.\]

Entonces:

Si$p(r)=0$ tiene raíces reales distintas$r_1$ y$r_2,$ entonces la solución general de la ecuación\ ref {eq:5.2.20} es\[y=c_1e^{r_1x}+c_2e^{r_2x}.\nonumber \]
Si$p(r)=0$ tiene una raíz repetida$r_1,$ entonces la solución general de la Ecuación\ ref {eq:5.2.20} es\[y=e^{r_1x}(c_1+c_2x).\nonumber \]
Si$p(r)=0$ tiene raíces conjugadas complejas$r_1=\lambda+i\omega$ y$r_2=\lambda-i\omega$$($ donde$\omega>0),$ entonces la solución general de la Ecuación\ ref {eq:5.2.20} es\[y=e^{\lambda x}(c_1\cos\omega x+c_2\sin\omega x).\nonumber \]