11.2: Serie I de Fourier
- Page ID
- 115058
En el Ejemplo 11.1.4 y Ejercicios 11.1.4-11.1.22 vimos que las funciones propias del Problema 5 son ortogonales\([-L,L]\) y las funciones propias de los Problemas 1—4 son ortogonales encendidas\([0,L]\). En esta sección y en la siguiente introducimos algunas expansiones de serie en términos de estas funciones propias. Usaremos estas expansiones para resolver ecuaciones diferenciales parciales en el Capítulo 12.
Supongamos que las funciones\(\phi_1,\)\(\phi_2,\)\(\phi_3,\)...\(,\) son ortogonales en\([a,b]\) y
\[\label{eq:11.2.1} \int_a^b\phi_n^2(x)\,dx\ne0,\quad n=1,2,3,\dots.\]
Que\(c_1,\)\(c_2,\)\(c_3,\)... sean constantes tales que las sumas parciales\(\displaystyle f_N(x)=\sum_{m=1}^N c_m\phi_m(x)\) satisfagan las desigualdades
\[|f_N(x)|\le M,\quad a\le x\le b,\quad N=1,2,3,\dots\nonumber \]
para alguna constante\(M<\infty.\) Supongamos también que la serie
\[\label{eq:11.2.2} f(x)=\sum_{m=1}^\infty c_m\phi_m(x)\]
converge y es integrable en\([a,b]\). Entonces
\[\label{eq:11.2.3} c_n={\displaystyle \int_a^bf(x)\phi_n(x)\,dx\over\displaystyle \int_a^b\phi_n^2(x)\,dx},\quad n=1,2,3,\dots.\]
- Prueba
-
Multiplicando la ecuación\ ref {eq:11.2.2} por\(\phi_n\) e integrando rendimientos
\[\label{eq:11.2.4} \int_a^b f(x)\phi_n(x)\,dx=\int_a^b \phi_n(x)\left(\sum_{m=1}^\infty c_m\phi_m(x)\right)\,dx.\]
Se puede demostrar que la delimitación de las sumas parciales\(\displaystyle \{f_N\}_{N=1}^\infty\) y la integrabilidad de\(f\) permiten intercambiar las operaciones de integración y suma a la derecha de la Ecuación\ ref {eq:11.2.4}, y reescribir la Ecuación\ ref {eq:11.2.4} como
\[\label{eq:11.2.5} \int_a^b f(x)\phi_n(x)\,dx=\sum_{m=1}^\infty c_m \int_a^b\phi_n(x) \phi_m(x)\,dx.\]
(Esto no es fácil de probar). Desde
\[\int_a^b\phi_n(x)\phi_m(x)\,dx=0\quad \text{if} \quad m\ne n,\nonumber \]
La ecuación\ ref {eq:11.2.5} reduce a
\[\int_a^bf(x) \phi_n(x)\,dx=c_n\int_a^b\phi_n^2(x)\,dx.\nonumber \]
Ahora la Ecuación\ ref {eq:11.2.1} implica Ecuación\ ref {eq:11.2.3}.
El teorema 11.2.1 motiva la siguiente definición.
Supongamos\(\phi_1,\)\(\phi_2\),...\(\phi_n\),,... son ortogonales en\([a,b]\) y\(\displaystyle \int_a^b\phi_n^2(x)\,dx\ne0\)\(n=1\),\(2\),,\(3\),... Dejar\(f\) ser integrable\([a,b],\) y definir
\[\label{eq:11.2.6} c_n={\displaystyle \int_a^bf(x)\phi_n(x)\,dx\over\displaystyle \int_a^b\phi_n^2(x)\,dx},\quad n=1,2,3,\dots.\]
Entonces la serie infinita\(\displaystyle \sum_{n=1}^\infty c_n\phi_n(x)\) se llama la expansión de Fourier de\(f\) en términos del conjunto ortogonal\(\displaystyle \{\phi_n\}_{n=1}^\infty\), y\(c_1\),\(c_2\),...,\(c_n\),... se llaman los coeficientes de Fourier de\(f\) con respecto a\(\displaystyle \{\phi_n\}_{n=1}^\infty\). Indicamos la relación entre\(f\) y su expansión de Fourier por
\[\label{eq:11.2.7} f(x)\sim\sum_{n=1}^\infty c_n\phi_n(x),\quad a\le x\le b.\]
Quizás te preguntes por qué no escribimos
\[f(x)=\sum_{n=1}^\infty c_n\phi_n(x),\quad a\le x\le b,\nonumber \]
en lugar de Ecuación\ ref {eq:11.2.7}. Desafortunadamente, esto no siempre es cierto. La serie de la derecha puede divergir para algunos o todos los valores de\(x\) in\([a,b]\), o puede converger\(f(x)\) para algunos valores de\(x\) y no para otros. Entonces, por ahora, solo pensaremos que la serie está asociada\(f\) a causa de la definición de los coeficientes\(\{c_n\}\), e indicaremos esta asociación informalmente como en la Ecuación\ ref {eq:11.2.7}.
Serie de Fourier
Ahora estudiaremos las expansiones de Fourier en términos de las funciones propias
\[1,\, \cos{\pi x\over L},\, \sin{\pi x\over L}, \, \cos{2\pi x\over L}, \, \sin{2\pi x\over L},\dots, \cos{n\pi x\over L}, \, \sin{n\pi x\over L},\dots.\nonumber \]
del Problema 5. Si\(f\) es integrable en\([-L,L]\), su expansión de Fourier en términos de estas funciones se llama la serie de Fourier de\(f\) on\([-L,L]\). Desde
\[\int_{-L}^L 1^2\,dx=2L,\nonumber \]
\[\int_{-L}^L\cos^2{n\pi x\over L}\,dx = \left.{1\over2}\int_{-L}^L\left(1+\cos{2n\pi x\over L}\right)\,dx= {1\over2}\left(x+{L\over2n\pi}\sin{2n\pi x\over L}\right) \right|_{-L}^{L}=L,\nonumber \]
y
\[\int_{-L}^L\sin^2{n\pi x\over L}\,dx = \left. {1\over2}\int_{-L}^L\left(1-\cos{2n\pi x\over L}\right)\,dx= {1\over2}\left(x-{L\over2n\pi}\sin{2n\pi x\over L}\right), \right|_{-L}^{L}=L,\nonumber \]
vemos en la Ecuación\ ref {eq:11.2.6} que la serie de Fourier de\(f\) on\([-L,L]\) es
\[a_0+\sum_{n=1}^\infty \left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right),\nonumber \]
donde
\[a_0={1\over 2L}\int_{-L}^L f(x)\,dx,\nonumber \]
\[a_n= {1\over L}\int_{-L}^L f(x)\cos{n\pi x\over L}\,dx,\quad \text{and} \quad b_n={1\over L}\int_{-L}^L f(x)\sin{n\pi x\over L}\,dx,\,n\ge1.\nonumber \]
Tenga en cuenta que\(a_0\) es el valor promedio de\(f\) on\([-L,L]\), mientras que\(a_n\) y\(b_n\) (for\(n\ge1\)) son el doble de los valores promedio de
\[f(x)\cos{n\pi x\over L}\quad\mbox{ and }\quad f(x)\sin{n\pi x\over L}\nonumber \]
en\([-L,L]\), respectivamente.
Convergencia de la serie de Fourier
La cuestión de la convergencia de las series de Fourier para funciones integrables arbitrarias está fuera del alcance de este libro. Sin embargo, podemos exponer un teorema que asiente esta pregunta para la mayoría de las funciones que surgen en las aplicaciones.
\(f\)Se dice que una función es lisa por partes\([a,b]\) si:
- \(f\)tiene como máximo finitamente muchos puntos de discontinuidad en\((a,b)\);
- \(f'\)existe y es continuo excepto posiblemente en finitamente muchos puntos en\((a,b)\);
- \(\displaystyle f(x_0+)=\lim_{x\to x_0+}f(x)\)y\(\displaystyle f'(x_0+)=\lim_{x\to x_0+}f'(x)\) existir si\(a\le x_0<b\);
- \(\displaystyle f(x_0-)=\lim_{x\to x_0-}f(x)\)y\(\displaystyle f'(x_0-)=\lim_{x\to x_0-}f'(x)\) existir si\(a< x_0\le b\).
Ya que\(f\) y\(f'\) se requiere que sean continuos en absoluto pero finitamente muchos puntos en\([a,b]\),\(f(x_0+)=f(x_0-)\) y\(f'(x_0+)=f'(x_0-)\) para todos menos finitamente muchos valores de\(x_0\) in\((a,b)\). Recordemos de la Sección 8.1 que\(f\) se dice que tiene una discontinuidad de salto en\(x_0\) si\(f(x_0+)\ne f(x_0-)\).
El siguiente teorema da condiciones suficientes para la convergencia de una serie de Fourier. La prueba está más allá del alcance de este libro.
Si\(f\) es poco uniforme\([-L,L]\), entonces la serie de Fourier
\[\label{eq:11.2.8}F(x)=a_{0}+\sum_{n=1}^{\infty}\left(a_{n}\cos\frac{n\pi x}{L}+b_{n}\sin\frac{n\pi x}{L} \right)\]de\(f\) on\([-L,L]\) converge para todos\(x\) en\([-L,L]\); además,
\[F(x)=\left\{\begin{array}{cc}{f(x),}&{\text{if }-L<x<L\text{ and }f\text{ is continuous at }x}\\{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }-L<x<L \text{ and }f \text{ is discontinuous at }x}\\{\dfrac{f(-L+)+f(L-)}{2},}&{\text{if }x=L\text{ or }x=-L}\end{array} \right.\nonumber\]
Ya que\(f(x+)=f(x-)\) si\(f\) es continuo en\(x\), también podemos decir que
\[F(x)=\left\{\begin{array}{cc}{\dfrac{f(x+)+f(x-)}{2},}&{\text{if }-L<x<L}\\{\dfrac{f(L-)+f(-L+)}{2},}&{\text{if }x=\pm L}\end{array} \right.\nonumber\]
Tenga en cuenta que\(F\) es en sí mismo por partes suave en\([-L,L]\), y\(F(x)=f(x)\) en todos los puntos en el intervalo abierto\((-L,L)\) donde\(f\) es continuo. Dado que la serie en Ecuación\ ref {eq:11.2.8} converge a\(F(x)\) for all\(x\) in\([-L,L]\), es posible que se vea tentado a inferir que el error
\[E_N(x)= \left|F(x)-a_0-\sum_{n=1}^N\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right)\right|\nonumber \]
se puede hacer tan pequeño como nos plazca para todos\(x\) en\([-L,L]\) eligiendo\(N\) suficientemente grande. Sin embargo, esto no es cierto si\(f\) tiene una discontinuidad en algún lugar\((-L,L)\), o si\(f(-L+)\ne f(L-)\). Aquí está la situación en este caso.
Si\(f\) tiene una discontinuidad de salto\(\alpha\) en un punto\((-L,L)\) adentro, habrá secuencias de puntos\(\{u_N\}\) y\(\{v_N\}\) en\((-L,\alpha)\) y\((\alpha,L)\), respectivamente, tal que
\[\lim _{N\to\infty}u_{N}=\lim _{N\to\infty}v_{N}=\alpha \nonumber \]
y
\[E_N(u_N)\approx .09|f(\alpha-)-f(\alpha+)| \quad \text{and} \quad E_N(v_N)\approx .09|f(\alpha-)-f(\alpha+)|.\nonumber \]
Así, el valor máximo del error\(E_N(x)\) cerca\(\alpha\) no se acerca a cero como\(N\to\infty\), sino que ocurre más y más cerca de\((\) y en ambos lados de\()\)\(\alpha\), y es esencialmente independiente de\(N\).
Si\(f(-L+)\ne f(L-)\), entonces habrá secuencias de puntos\(\{u_N\}\) y\(\{v_N\}\) en\((-L,L)\) tal que
\[\lim_{N\to\infty}u_N=-L,\quad \lim_{N\to\infty}v_N=L,\nonumber \]
\[E_N(u_N)\approx .09|f(-L+)-f(L-)| \quad \text{and} \quad E_N(v_N)\approx .09|f(-L+)-f(L-)|.\nonumber \]
Este es el fenómeno Gibbs. Habiendo sido alertado de ello, es posible que lo veas en las figuras 11.2.2 - 11.2.4 , a continuación; sin embargo, daremos un ejemplo específico al final de esta sección.
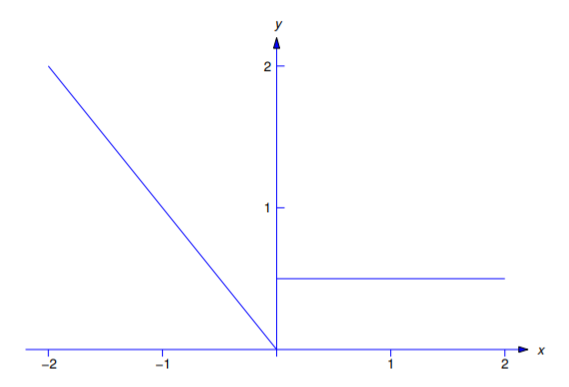
Encuentre la serie de Fourier de la función suave por partes
\[f(x)= \left\{\begin{array}{rlr} -x,&-2< x<0, \\{1\over2},&\phantom{-}0<x<2 \end{array}\right.\nonumber \]
on\([-2,2]\) (Figura 11.2.1 ). Determinar la suma de la serie de Fourier para\(-2\le x\le 2\).
Solución
Tenga en cuenta que no nos molestamos en definir\(f(-2)\),\(f(0)\), y\(f(2)\). No importa cómo se puedan definir,\(f\) es uniforme por partes y los coeficientes en la serie de Fourier\([-2,2]\)
\[F(x)=a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over2}+b_n\sin{n\pi x\over2}\right)\nonumber \]
no se ven afectados por ellos. En cualquier caso, el teorema 11.2.4 implica que\(F(x)=f(x)\) en\((-2,0)\) y\((0,2)\), donde\(f\) es continuo, mientras
\[F(-2)=F(2)={f(-2+)+f(2-)\over2}= {1\over2}\left(2+{1\over2}\right)={5\over4}\nonumber \]
y
\[F(0)={f(0-)+f(0+)\over2}={1\over2}\left(0+{1\over2}\right)={1\over4}.\nonumber \]
Para resumir,
\[F(x)= \left\{\begin{array}{rl} {5\over4},&\phantom{-}x=-2\\ -x,&-2<x<0,\\ {1\over4},&\phantom{-}x=0,\\ {1\over2},&\phantom{-}0<x<2,\\ {5\over4},&\phantom{-}x=2. \end{array}\right.\nonumber \]
Calculamos los coeficientes de Fourier de la siguiente manera:
\[a_0={1\over4}\int_{-2}^2f(x)\,dx={1\over4}\left[\int_{-2}^0(-x)\,dx +\int_0^2{1\over2}\,dx\right] ={3\over4}.\nonumber \]
Si\(n\ge1\), entonces
\[\begin{aligned} a_n&={1\over2}\int_{-2}^2f(x)\cos{n\pi x\over2}\,dx={1\over2}\left[\int_{-2}^0(-x)\cos{n\pi x\over2}\,dx +\int_0^2{1\over2}\cos{n\pi x\over2}\,dx\right]\\&={2\over n^2\pi^2}(\cos n\pi-1),\end{aligned}\nonumber \]
y
\[\begin{aligned} b_n&={1\over2}\int_{-2}^2f(x)\sin{n\pi x\over2}\,dx={1\over2}\left[\int_{-2}^0(-x)\sin{n\pi x\over2}\,dx +\int_0^2{1\over2}\sin{n\pi x\over2}\,dx\right]\\ &={1\over2n\pi}(1+3\cos n\pi).\end{aligned}\nonumber \]
Por lo tanto
\[F(x)={3\over4}+{2\over\pi^2}\sum_{n=1}^\infty{\cos n\pi-1\over n^2}\cos{n\pi x\over2}+{1\over2\pi}\sum_{n=1}^\infty{1+3\cos n\pi\over n}\sin{n\pi x\over2}.\nonumber \]
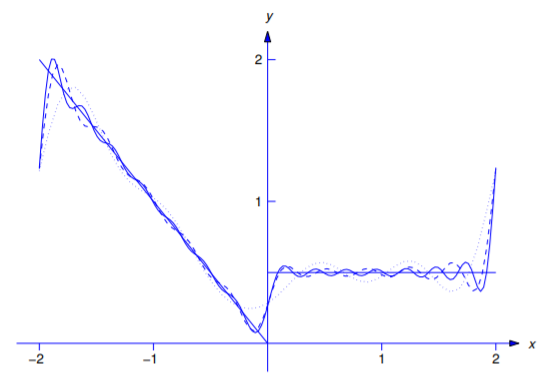
La figura 11.2.2 muestra cómo la suma parcial
\[F_m(x)={3\over4}+{2\over\pi^2}\sum_{n=1}^m{\cos n\pi-1\over n^2}\cos{n\pi x\over2}+{1\over2\pi}\sum_{n=1}^m{1+3\cos n\pi\over n}\sin{n\pi x\over2}\nonumber \]
se aproxima\(f(x)\) para\(m=5\) (curva punteada),\(m=10\) (curva discontinua) y\(m=15\) (curva sólida).
Funciones pares e impares
Calcular los coeficientes de Fourier de una función\(f\) puede ser tedioso; sin embargo, el cálculo a menudo puede simplificarse explotando simetrías en\(f\) o algunos de sus términos. Para enfocarnos en esto, recordamos algunos conceptos que estudiaste en cálculo. Dejar\(u\) y\(v\) ser definido\([-L,L]\) y supongamos que
\[u(-x)=u(x)\quad\mbox{ and }\quad v(-x)=-v(x),\quad -L\le x\le L.\nonumber \]
Entonces decimos que\(u\) es una función par y\(v\) es una función impar. Tenga en cuenta que:
- El producto de dos funciones pares es parejo.
- El producto de dos funciones impares es par.
- El producto de una función par y una función impar es impar.
Las funciones\(u(x)=\cos \omega x\) y\(u(x)=x^2\) son pares, mientras\(v(x)=\sin \omega x\) y\(v(x)=x^3\) son impares. La función no\(w(x)=e^x\) es ni par ni impar.
Aprendiste las partes (a) y (b) del siguiente teorema en el cálculo, y las otras partes siguen de ellas (Ejercicio 11.2.1).
Supongamos que\(u\) es par y\(v\) es impar en\([-L,L].\) Entonces:
- \(\displaystyle \int_{-L}^L u(x)\,dx=2\int_0^Lu(x) \,dx,\)
- \(\displaystyle \int_{-L}^L v(x)\,dx=0,\)
- \(\displaystyle \int_{-L}^L u(x)\cos{n\pi x\over L}\,dx=2\int_0^Lu(x)\cos{n\pi x\over L} \,dx,\)
- \(\displaystyle \int_{-L}^L v(x)\sin{n\pi x\over L}\,dx= 2\int_0^L v(x)\sin{n\pi x\over L}\,dx,\)
- \(\displaystyle \int_{-L}^L u(x)\sin{n\pi x\over L}\,dx=0\)
- \(\displaystyle \int_{-L}^L v(x)\cos{n\pi x\over L}\,dx=0.\)
Encuentre la serie de Fourier de\(f(x)=x^2-x\) on\([-2,2]\), y determine su suma para\(-2\le x\le 2\).
Solución
Dado que\(L=2\),
\[F(x)=a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over2}+b_n\sin{n\pi x\over2}\right)\nonumber \]
donde
\[\label{eq:11.2.9} a_0={1\over4}\int_{-2}^2(x^2-x)\,dx,\]
\[\label{eq:11.2.10} a_n={1\over2}\int_{-2}^2(x^2-x)\cos{n\pi x\over2}\,dx,\quad n=1,2,3,\dots,\]
y
\[\label{eq:11.2.11} b_n={1\over2}\int_{-2}^2(x^2-x)\sin{n\pi x\over2}\,dx,\quad n=1,2,3,\dots.\]
Simplificamos la evaluación de estas integrales mediante el uso del Teorema 11.2.5 con\(u(x)=x^2\) y\(v(x)=x\); así, a partir de la Ecuación\ ref {eq:11.2.9},
\[a_0=\left.{1\over2}\int_0^2x^2\,dx={x^3\over6}\right| _{0}^{2}={4\over3}.\nonumber \]
De la ecuación\ ref {eq:11.2.10},
\[\begin{aligned} a_n&=\int_0^2x^2\cos{n\pi x\over2}\,dx= \left.{2\over n\pi}\left[x^2\sin{n\pi x\over2}\right| _{0}^{2}- 2\int_0^2x\sin{n\pi x\over2}\,dx\right]\\ &=\left. {8\over n^2\pi^2}\left[x\cos{n\pi x\over2}\right| _{0}^{2}- \int_0^2\cos{n\pi x\over2}\,dx\right]\\ &=\left.{8\over n^2\pi^2}\left[2\cos n\pi-{2\over n\pi}\sin{n\pi x\over2}\right|_{0}^{2}\right] =(-1)^n{16\over n^2\pi^2}.\end{aligned}\nonumber \]
De la ecuación\ ref {eq:11.2.11},
\[\begin{aligned} b_n&=-\int_0^2x\sin{n\pi x\over2}\,dx =\left. {2\over n\pi}\left[x\cos{n\pi x\over2}\right|_{0}^{2}- \int_0^2\cos{n\pi x\over2}\,dx\right]\\ &=\left.{2\over n\pi}\left[2\cos n\pi-{2\over n\pi}\sin{n\pi x\over2}\right|_{0}^{2} \right]=(-1)^n{4\over n\pi}.\end{aligned}\nonumber \]
Por lo tanto
\[F(x)={4\over3}+{16\over\pi^2}\sum_{n=1}^\infty{(-1)^n\over n^2} \cos{n\pi x\over2}+{4\over\pi}\sum_{n=1}^\infty {(-1)^n\over n}\sin{n\pi x\over2}.\nonumber \]
El teorema 11.2.4 implica que
\[F(x)= \left\{\begin{array}{cl} 4,&\phantom{-}x=-2,\\ x^2-x,&-2<x<2,\\4,&\phantom{-}x=2. \end{array}\right.\nonumber \]
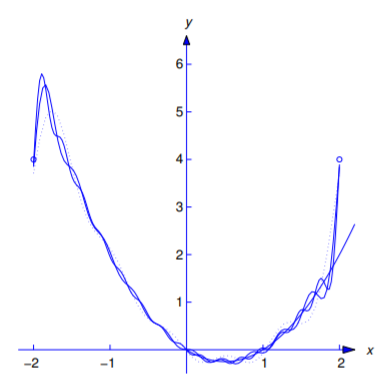
La figura 11.2.3 muestra cómo la suma parcial
\[F_m(x)={4\over3}+{16\over\pi^2}\sum_{n=1}^m{(-1)^n\over n^2} \cos{n\pi x\over2}+{4\over\pi}\sum_{n=1}^m {(-1)^n\over n}\sin{n\pi x\over2}\nonumber \]
se aproxima\(f(x)\) para\(m=5\) (curva punteada),\(m=10\) (curva discontinua) y\(m=15\) (curva sólida).
El teorema 11.2.5 implica el siguiente teorema.
Supongamos que\(f\) es integrable en\([-L,L].\)
- Si\(f\) es incluso\(,\) la serie de Fourier de\(f\) on\([-L,L]\) es\[F(x)=a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L},\nonumber \] donde\[a_0={1\over L}\int_0^Lf(x) \,dx \quad \text{and} \quad a_n={2\over L}\int_0^L f(x)\cos{n\pi x\over L}\,dx,\quad n\ge1.\nonumber \]
- Si\(f\) es impar\(,\) la serie de Fourier de\(f\) on\([-L,L]\) es\[F(x)= \sum_{n=1}^\infty b_n \sin{n\pi x\over L},\nonumber \] donde\[b_n={2\over L}\int_0^L f(x)\sin{n\pi x\over L}\,dx.\nonumber \]
Encuentre la serie de Fourier de\(f(x)=x\) on\([-\pi,\pi]\), y determine su suma para\(-\pi\le x\le \pi\).
Solución
Dado que\(f\) es impar y\(L=\pi\),
\[F(x)=\sum_{n=1}^\infty b_n\sin nx\nonumber \]
donde
\[\begin{aligned} b_n&={2\over\pi}\int_0^\pi x\sin nx\,dx=\left. -{2\over n\pi}\left[x\cos nx\right|_{0}^{\pi }-\int_0^\pi\cos nx\,dx\right]\\ &=\left.-{2\over n}\cos n\pi+{2\over n^2\pi}\sin nx\right|_{0}^{\pi }=(-1)^{n+1} {2\over n}.\end{aligned}\nonumber \]
Por lo tanto
\[F(x)=-2\sum_{n=1}^\infty{(-1)^n\over n}\sin nx.\nonumber \]
El teorema 11.2.4 implica que
\[F(x)= \left\{\begin{array}{cl} 0,&\phantom{-}x=-\pi,\\ x,&-\pi<x<\pi,\\0,&\phantom{-}x=\pi. \end{array}\right.\nonumber \]
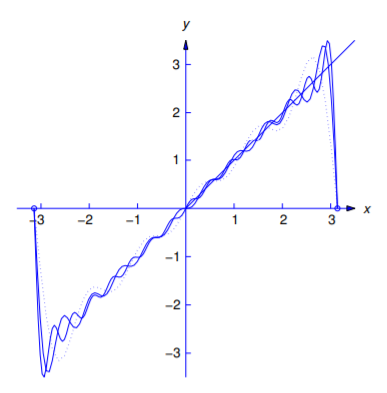
La figura 11.2.4 muestra cómo la suma parcial
\[F_m(x)=-2\sum_{n=1}^m{(-1)^n\over n}\sin nx\nonumber \]
se aproxima\(f(x)\) para\(m=5\) (curva punteada),\(m=10\) (curva discontinua) y\(m=15\) (curva sólida).
Encuentre la serie de Fourier de\(f(x)=|x|\) on\([-\pi,\pi]\) y determine su suma para
\(-\pi\le x\le\pi\).
Solución:
Ya que\(f\) es parejo y\(L=\pi\),
\[F(x)=a_0+\sum_{n=1}^\infty a_n\cos nx.\nonumber \]
Ya que\(f(x)=x\) si\(x\ge0\),
\[a_0=\left. {1\over\pi}\int_0^\pi x\,dx={x^2\over2\pi}\right|_{0}^{\pi }={\pi\over2}\nonumber \]
y, si\(n\ge1\),
\[\begin{aligned} a_n&=\left.{2\over\pi}\int_0^\pi x\cos nx\,dx={2\over n\pi}\left[x\sin nx\right|_{0}^{\pi }-\int_0^\pi\sin nx\,dx\right]\\ &=\left.{2\over n^2\pi}\cos nx\right|_{0}^{\pi }=\frac{2}{n^2\pi}(\cos n\pi-1)={2\over n^2\pi}[(-1)^n-1].\end{aligned}\nonumber \]
Por lo tanto
\[\label{eq:11.2.12} F(x)={\pi\over2}+{2\over\pi}\sum_{n=0}{(-1)^n-1\over n^2}\cos nx.\]
Sin embargo, desde
\[(-1)^n-1= \left\{\begin{array}{rl} 0&\mbox{ if }n=2m,\\ -2&\mbox{ if }n=2m+1, \end{array}\right.\nonumber \]
los términos en la Ecuación\ ref {eq:11.2.12} para los cuales\(n=2m\) son todos ceros. Por lo tanto solo incluimos los términos para los cuales\(n=2m+1\); es decir, podemos reescribir la Ecuación\ ref {eq:11.2.12} como
\[F(x)={\pi\over2}-{4\over\pi}\sum_{m=0}^\infty {1\over(2m+1)^2} \cos(2m+1)x.\nonumber \]
Sin embargo, dado que el nombre del índice de suma no importa, preferimos reemplazarlo\(m\) por\(n\), y escribir
\[F(x)={\pi\over2}-{4\over\pi}\sum_{n=0}^\infty {1\over(2n+1)^2} \cos(2n+1)x.\nonumber \]
Ya que\(|x|\) es continuo para todos\(x\) y\(|-\pi|=|\pi|\), Teorema 11.2.4 implica que\(F(x)=|x|\) para todos\(x\) en\([-\pi,\pi]\).
Encuentre la serie de Fourier de\(f(x)=x(x^2-L^2)\) on\([-L,L]\), y determine su suma para\(-L\le x\le L\).
Solución:
Dado que\(f\) es impar,
\[F(x)=\sum_{n=1}^\infty b_n\sin\frac{n\pi x}{L},\nonumber \]
donde
\[\begin{aligned} b_n&={2\over L}\int_0^Lx(x^2-L^2)\sin{n\pi x\over L}\,dx\\ &\left.=-{2\over n\pi}\left[x(x^2-L^2)\cos{n\pi x\over L}\right|_{0}^{L}- \int_0^L (3x^2-L^2)\cos{n\pi x\over L}\,dx\right]\\ &=\left.{2L\over n^2\pi^2}\left[(3x^2-L^2)\sin{n\pi x\over L}\right|_{0}^{L}-6 \int_0^Lx\sin{n\pi x\over L}\,dx\right]\\ &=\left.{12L^2\over n^3\pi^3}\left[x\cos{n\pi x\over L}\right|_{0}^{L}- \int_0^L\cos{n\pi x\over L}\,dx\right] =(-1)^n{12L^3\over n^3\pi^3}.\end{aligned}\nonumber \]
Por lo tanto
\[F(x)={12L^3\over\pi^3}\sum_{n=1}^\infty{(-1)^n\over n^3}\sin{n\pi x\over L}.\nonumber \]
El teorema 11.2.4 implica que\(F(x)=x(x^2-L^2)\) para todos\(x\) en\([-L,L]\).
La serie de Fourier de
\[f(x)=\left\{\begin{array}{cl} 0,&-1<x<-{1\over2},\\ 1,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\nonumber \]
on\([-1,1]\) es
\[F(x)={1\over2}+{2\over\pi}\sum_{n=1}^\infty {(-1)^{n-1}\over2n-1}\cos(2n-1)\pi x.\nonumber \]
(Verificar.) Según el Teorema 11.2.4 ,
\[F(x)=\left\{\begin{array}{cl} 0,&-1\le x<-{1\over2},\\ {1\over2},& x=-{1\over2},\\ 1,&-{1\over2}<x<{1\over2},\\ {1\over2},& x={1\over2},\\ 0,&{1\over2}<x\le 1; \end{array}\right.\nonumber \]
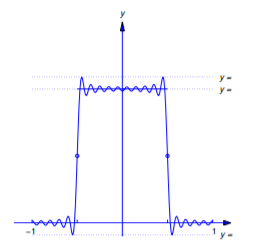
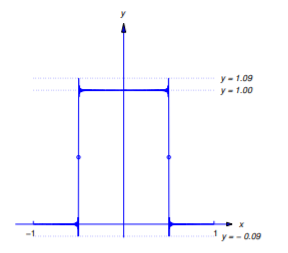
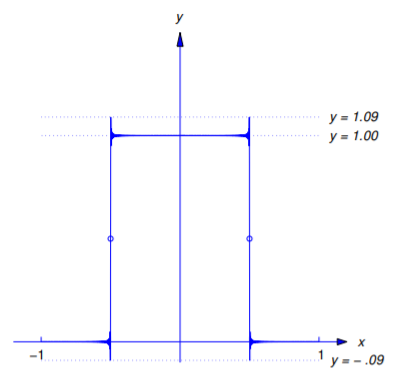
por lo tanto,\(F\) (así como\(f\)) tiene discontinuidades de salto de unidad en\(x=\pm\frac{1}{2}\). Las figuras 11.2.5 - 11.2.7 muestran las gráficas de\(y=f(x)\) y
\[y=F_{2N-1}(x)=\frac{1}{2}+ {2\over\pi}\sum_{n=1}^N {(-1)^{n-1}\over2n-1}\cos(2n-1)\pi x\nonumber \]
para\(N=10\),\(20\), y\(30\). Se puede ver que aunque\(F_{2N-1}\) se aproxima\(F\) (y por lo tanto\(f\)) bien en intervalos mayores a medida que\(N\) aumenta, los valores absolutos máximos de los errores permanecen aproximadamente iguales a\(.09\), pero ocurren más cerca de las discontinuidades a\(x=\pm\frac{1}{2}\) medida que\(N\) aumenta.
Uso de la tecnología
El cálculo de los coeficientes de Fourier será tedioso en muchos de los ejercicios de este capítulo y del siguiente. Para aprender la técnica, te recomendamos que hagas algunos ejercicios en cada sección “a mano”, quizás usando la tabla de integrales al frente del libro. No obstante, te animamos a usar tu software de cómputo simbólico favorito en los problemas más difíciles.


