1.3: Aplicaciones
- Page ID
- 119659
EN ESTA SECCIÓN VEREMOS ALGUNAS APLICACIONES SIMPLES QUE SE MODELAN CON ECUACIONES DIFERENCIALES Comenzaremos con modelos exponenciales simples de crecimiento y decaimiento.
Crecimiento y Decaimiento
ALGUNOS DE LOS MODELOS MÁS SIMPLES SON LOS QUE INVEN Por ejemplo, un modelo poblacional se puede obtener bajo suposiciones simples. Que\(P(t)\) sea la población en el momento\(t\). Queremos encontrar una expresión para la tasa de cambio de la población,\(\dfrac{d P}{d t}\). Suponiendo que no hay migración de población, la única forma en que la población puede cambiar es sumando o restando individuos en la población. La ecuación tomaría la forma
\(\dfrac{d P}{d t}=\text { Rate In }-\text { Rate Out. }\)
La Tasa In podría deberse al número de nacimientos por unidad de tiempo y a la Tasa de Salida por el número de muertes por unidad de tiempo. Las formas más simples para estas tarifas serían dadas por
\(\text { Rate In }=b P \text { and the Rate Out }=m P .\)
Aquí hemos denotado la tasa de natalidad como\(b\) y la tasa de mortalidad como\(m\). Esto da la tasa total de cambio de la población como
\[\dfrac{d P}{d t}=b P-m P \equiv k P \label{1.27} \]
La ecuación\(\PageIndex{1}\) es una ecuación separable. La separación sigue como hemos visto anteriormente en el capítulo. Reordenando la ecuación, su forma diferencial es
\(\dfrac{d P}{P}=k d t\)
Integrando, tenemos
\[ \begin{aligned} &\int \dfrac{d P}{P}=\int k d t \\ &\ln |P|=k t+C \end{aligned} \label{1.28} \]
A continuación, resolvemos para\(P(t)\) a través de la exponenciación, integrando, tenemos
\[ \begin{aligned} |P(t)| &=e^{k t+C} \\ P(t) &=\pm e^{k t+C} \\ &=\pm e^{C} e^{k t} \\ &=A e^{k t} . \end{aligned}\label{1.29} \]
De manera más general, el problema del valor inicial\(d P / d t=k P, P\left(t_{0}\right)=P_{0}\) tiene la solución\(P(t) P_0 e^{k(t-t_0)}\).
Aquí cambiamos el nombre de la constante arbitraria,\(\pm e^{C}\), como\(A .\)
Si la población a\(t=0\) es\(P_{0}\), es decir\(P(0)=P_{0}\), entonces la solución da\(P(0)=A e^{0}=A=P_{0} .\) Entonces, la solución del problema de valor inicial es
\(P(t)=P_{0} e^{k t}\)
Crecimiento poblacional maltusiano.
Ecuación\(\PageIndex{1}\) del modelo exponencial familiar de crecimiento poblacional:
\(\dfrac{d P}{d t}=k P\)
Esto se resuelve fácilmente y se obtiene crecimiento\((k>0)\) o decaimiento exponencial\((k<0)\).
Este modelo de crecimiento maltusiano lleva el nombre de Thomas Robert Malthus\((1766-1834)\), un clérigo que utilizó este modelo para advertir de la inminente fatalidad de la raza humana si sus prácticas reproductivas continuaban.
Considera una población de bacterias de peso\(20 \mathrm{~g}\). Si la población se duplica cada 20 minutos, entonces ¿cuál es la población después de 30 minutos? [Nota: Es más fácil pesar esta población que contarla.]
Uno mira la información dada antes de intentar responder a la pregunta. Primero, tenemos la condición inicial\(P_{0}=20 \mathrm{~g}\). Ya que la población se duplica cada 20 minutos, entonces\(P(20)=2 P_{0}=40\). Aquí tenemos tomar las unidades de tiempo como minutos. Entonces se nos pide que encontremos\(P(30)\).
No necesitamos resolver la ecuación diferencial. Asumiremos un modelo de crecimiento simple. Usando la solución general\(P(t)=20 e^{k t}\),, tenemos
\(P(20)=20 e^{20 k}=40\)
o
\(e^{20 k}=2\)
Podemos resolver esto por\(k\),
\(20 k=\ln 2, \quad \Rightarrow k=\dfrac{\ln 2}{20} \approx 0.035\)
Esto da una solución aproximada,\(P(t) \approx 20 e^{.035 t} .\) ahora podemos responder a la pregunta original. A saber,\(P(30) \approx 57 .\)
Por supuesto, podríamos obtener una solución exacta. Con algunas manipulaciones simples, tenemos
\[ \begin{aligned} P(t) &=20 e^{k t} \\ &=20 e^{\left(\dfrac{\ln 2}{20}\right) t} \\ &=20\left(e^{\ln 2}\right)^{\dfrac{t}{20}} \\ &=20\left(2^{\dfrac{t}{20}}\right) \end{aligned} \label{1.30} \]
Esta respuesta toma la forma general para duplicar la población,\(P(t)=\)\(P_{0} 2^{\dfrac{t}{\tau}}\), donde\(\tau\) está la tasa de duplicación.
Otro problema estándar de crecimiento y desintegración es la desintegración radiactiva. Ciertos isótopos son inestables y el núcleo se rompe, lo que lleva a la desintegración nuclear. Los productos de la descomposición también pueden ser inestables y sufrir más desintegración nuclear. Como ejemplo, el uranio-238 (U-238) se descompone en torio-234 (Th-Radioactive decay problems. 234). El torio-234 es inestable y se desintegra en Protactinium (Pa-234). Esto a su vez decae en muchos pasos hasta que se produce plomo (Pb-206) como se muestra en la Tabla\(\PageIndex{1}\). Este isótopo de plomo es estable y el proceso de descomposición se detiene. Si bien esta es una forma de desintegración radiactiva, existen otros tipos. Por ejemplo, Radón 222 (Rn-222) cede una partícula alfa (núcleo de helio) dejando Polonio (Po-218).
| Isótopo | Vida media |
|---|---|
| \(U^{238}\) | \(4.468 x 10^{9}\)años |
| \(T h^{234}\) | \(24.1\)días |
| \(P a^{234 m}\) | \(1.17\)minutos |
| \(U^{234}\) | \(2.47 x 10^{5}\)años |
| \(T h^{230}\) | \(8.0 x 10^{4}\)años |
| \(R a^{226}\) | 1602 años |
| \(R n^{222}\) | \(3.823\)días |
| \(P o^{218}\) | \(3.05\)minutos |
| \(P b^{214}\) | \(26.8\)minutos |
| \(B i^{214}\) | \(19.7\)minutos |
| \(P o^{214}\) | 164 microseg |
| \(P b^{210}\) | 21 años |
| \(B i^{210}\) | \(5.01\)días |
| \(P o^{210}\) | \(138.4\)días |
| \(P b^{206}\) | estable |
Dada una cierta cantidad de material radiactivo, no todo se descompone a la vez. Una medida de la tendencia de un núcleo a descomponerse se llama la vida media. Este es el tiempo que tarda la mitad del material en descomponerse. Esto es similar al último ejemplo y se puede entender usando un ejemplo sencillo.
Si\(150.0 \mathrm{~g}\) de Torio-234 decae a\(137.6 \mathrm{~g}\) de Torio234 en tres días, ¿cuál es su vida media?
Este es otro proceso de descomposición simple. Si\(Q(t)\) representa la cantidad de material inestable, entonces\(Q(t)\) satisface la ecuación de tasa
\(\dfrac{d Q}{d t}=k Q\)
con\(k<0 .\) La solución del problema de valor inicial, como hemos visto, es\(Q(t)=Q_{0} e^{k t}\).
Ahora, dejemos que la vida media sea dada por\(\tau\). Entonces,\(Q(\tau)=\dfrac{1}{2} Q_{0}\). Insertando este hecho en la solución, tenemos
\[ \begin{aligned} Q(\tau) &=Q_{0} e^{k \tau} \\ \dfrac{1}{2} Q_{0} &=Q_{0} e^{k \tau} \\ \dfrac{1}{2} &=e^{k \tau} \end{aligned} \label{1.31} \]
Señalando que\(Q(t)=Q_{0}\left(e^{k}\right)^{t}\), resolvemos la Ecuación\(\PageIndex{5}\) para
\(e^{k}=2^{-1 / \tau}\)
Entonces, la solución se puede escribir en la forma general
\(Q(t)=Q_{0} 2^{-\dfrac{t}{\tau}}\)
Tenga en cuenta que la constante de decadencia es\(k=-\dfrac{\ln 2}{\tau}<0\).
Volviendo al problema, se nos da
\(Q(3)=1502^{-\dfrac{3}{\tau}}=137.6\)
Resolviendo a\(\tau\),
\[ \begin{aligned} 2^{-\dfrac{3}{\tau}} &=\dfrac{136.7}{150} \\ -3 \ln 2 &=\ln .9173 \tau \\ \tau &=-\dfrac{3 \ln 2}{\ln .9173}=24.09 \end{aligned} \nonumber \]
Por lo tanto, la vida media es de aproximadamente\(24.1\) días.
Ley de Refrigeración de Newton
SI TOMAS TU TAZA DE TÉ CALIENTE, y la dejas reposar en una habitación fría, el té se enfriará y alcanzará la temperatura ambiente después de un periodo de tiempo. La ley del enfriamiento se atribuye a Isaac Newton (1642-1727) quien probablemente fue el primero en exponer resultados sobre cómo se enfrían los cuerpos. \({ }^{1}\)La idea principal es que un cuerpo atemperatura\(T(t)\) está inicialmente a temperatura\(T(0)=T_{0} .\) Se coloca en un ambiente a una temperatura ambiente de\(T_{a}\). Se da un modelo sencillo que la tasa de cambio de la temperatura del cuerpo es proporcional a la diferencia entre la temperatura corporal y su entorno. Por lo tanto, tenemos
\(\dfrac{dT}{dt} \propto T -T_a\)
La proporcionalidad se elimina mediante la introducción de una constante de enfriamiento.
\[\dfrac{d T}{d t}=-k\left(T-T_{a}\right) \label{1.33} \]
donde\(k>0\).
- 1
-
La Ley 1701 de Enfriamiento de Newton es una aproximación a cómo los cuerpos se enfrían para pequeñas diferencias de temperatura\(\left(T-T_{a} \ll T\right)\) y no toma en cuenta todos los procesos de enfriamiento. Una cuenta la da C. T. O'Sullivan, Am. J. Phys (1990) p. 956-960.
Esta ecuación diferencial se puede resolver señalando que la ecuación se puede escribir en la forma
\(\dfrac{d}{d t}\left(T-T_{a}\right)=-k\left(T-T_{a}\right)\)
Esto es ahora de la forma de decaimiento exponencial de la función\(T(t)-T_{a}\). La solución se encuentra fácilmente como
\(T(t)-T_{a}=\left(T_{0}-T_{a}\right) e^{-k t}\)
O
\(T(t)=T_{a}+\left(T_{0}-T_{a}\right) e^{-k t}\)
Una taza de té se\(90^{\circ} \mathrm{C}\) enfría a\(85^{\circ} \mathrm{C}\) en diez minutos. Si la temperatura ambiente es\(22^{\circ} \mathrm{C}\), ¿cuál es su temperatura después de 30 minutos?
Usando la solución general con\(T_{0}=90^{\circ} \mathrm{C}\),
\(T(t)=22+(90-22) e^{-k}=22+68 e^{-k t}\)
luego encontramos\(k\) usando la información dada,\(T(10)=85^{\circ} \mathrm{C}\). Tenemos
\[ \begin{aligned} 85 &=T(10) \\ &=22+68 e^{-10 k} \\ 63 &=68 e^{-10 k} \\ e^{-10 k} &=\dfrac{63}{68} \approx 0.926 \\ -10 k &=\ln 0.926 \\ k &=-\dfrac{\ln 0.926}{10}=0.00764 \end{aligned}\end{equation}\label{1.34} \]
Esto da la ecuación para este modelo como
([T (t) =22+68 e^ {-0.00764 t}\)
Ahora ya podemos responder a la pregunta. ¿Qué es\(T(30) ?\)
\(T(30)=22+68 e^{-0.00764(30)}=76^{\circ} \mathrm{C}\)
Velocidad terminal
AHORA VOLVAMOS A LA CAÍDA LIBRE. ¿Y si hay resistencia al aire? Primero necesitamos modelar la resistencia del aire. A medida que un objeto cae cada vez más rápido, la fuerza de arrastre se vuelve mayor. Entonces, esta fuerza resistiva es una función de la velocidad. Hay un par de modelos estándar que la gente usa para probar esto. La idea es escribir\(F=m a\) en la forma
\[m \ddot{y}=-m g+f(v) \nonumber \]
donde\(f(v)\) da la fuerza resistiva y\(m g\) es el peso. Recordemos que esto se aplica a la caída libre cerca de la superficie de la Tierra. También, para que sea resistiva,\(f(v)\) debe oponerse a la moción. Si el cuerpo está cayendo, entonces\(f(v)\) debería ser positivo. Si está subiendo, entonces\(f(v)\) tendría que ser negativo para indicar la oposición a la moción.
Una determinación común deriva de la fuerza de arrastre sobre un objeto que se mueve a través de un fluido. Esta fuerza viene dada por
\[f(v)=\dfrac{1}{2} C A \rho v^{2} \nonumber \]
donde\(C\) está el coeficiente de arrastre,\(A\) es el área de la sección transversal y\(\rho\) es la densidad del fluido. Para el flujo laminar el coeficiente de arrastre es constante.
A menos que te interese en la aerodinámica, no necesitas entrar en los detalles de las constantes. Entonces, lo mejor es absorber todas las constantes en una sola para simplificar el cálculo. Entonces, vamos a escribir\(f(v)=b v^{2}\). La ecuación diferencial incluyendo arrastre puede ser reescrita como
\[\dot{v}=k v^{2}-g \nonumber \]
donde\(k=b / m\). Tenga en cuenta que esta es una ecuación de primer orden para\(v(t)\). ¡También es separable! Formalmente, podemos separar las variables e integrarlas a lo largo del tiempo para obtener
\[t+K=\int^{v} \dfrac{d z}{k z^{2}-g} \nonumber \]
Este es el primer uso de Descomposición de Fracción Parcial. Exploraremos este método más a fondo en la sección sobre Transformas de Laplace.
(Nota: Se utilizó una constante de integración de\(K\) ya que\(C\) es el coeficiente de arrastre en este problema.) Si podemos hacer la integral, entonces tenemos una solución para v. De hecho, podemos hacer esta integral. Es necesario recordar otro método común de integración, que aún no hemos revisado. ¿Recuerdas Descomposición Parcial de Fracciones? Implica factorizar el denominador en la integral. En el caso más simple hay dos factores lineales en el denominador y se reescribe la integral:
\[\int \dfrac{d x}{(x-a)(x-b)}=\dfrac{1}{b-a} \int\left[\dfrac{1}{x-a}-\dfrac{1}{x-b}\right] d x \nonumber \]
La nueva integral tiene ahora dos términos que pueden integrarse fácilmente.
Para factorizar el denominador en el problema actual, primero tenemos que reescribir las constantes. Dejamos\(\alpha^{2}=g / k\) y escribimos el integrand como
\[\dfrac{1}{k z^{2}-g}=\dfrac{1}{k} \dfrac{1}{z^{2}-\alpha^{2}} \nonumber \]
Ahora utilizamos una descomposición parcial de la fracción para obtener
\[\dfrac{1}{k z^{2}-g}=\dfrac{1}{2 \alpha k}\left[\dfrac{1}{z-\alpha}-\dfrac{1}{z+\alpha}\right] \nonumber \]
Ahora, el integrand se puede integrar fácilmente dando
\[t+K=\dfrac{1}{2 \alpha k} \ln \left|\dfrac{v-\alpha}{v+\alpha}\right| \nonumber \]
Resolviendo para\(v\), tenemos
\[v(t)=\dfrac{1-B e^{2 \alpha k t}}{1+B e^{2 \alpha k t}} \alpha \nonumber \]
donde se\(B \equiv e^{K} . B\) puede determinar usando la velocidad inicial.
Existen otras formas para la solución en términos de una función tanh, que el lector puede determinar como ejercicio. Una conclusión importante es que para grandes tiempos, la relación en la solución se acerca\(-1 .\) Así,\(v \rightarrow-\alpha=\)\(-\sqrt{\dfrac{g}{k}}\) como\(t \rightarrow \infty\). Esto significa que el objeto que cae alcanzará una velocidad terminal constante.
Como simple cálculo, podemos determinar la velocidad terminal. Tomaremos un\(80 \mathrm{~kg}\) paracaidista con un área de sección transversal de aproximadamente\(0.093 \mathrm{~m}^{2}\). (El paracaidista está cayendo de cabeza primero.) Supongamos que la densidad del aire es una constante\(1.2 \mathrm{~kg} / \mathrm{m}^{3}\) y el coeficiente de arrastre lo es\(C=2.0\). Primero notamos que
\(v_{\text {terminal }}=-\sqrt{\dfrac{g}{k}}=-\sqrt{\dfrac{2 m g}{C A \rho}}\)
Entonces,
\(v_{\text {terminal }}=-\sqrt{\dfrac{2(70)(9.8)}{(2.0)(0.093)(1.2)}}=-78 \mathrm{~m} / \mathrm{s}\)
Esto es aproximadamente\(175 \mathrm{mph}\), que es ligeramente superior a la velocidad terminal real de un buceador del cielo con brazos y pies completamente extendidos. Se necesitaría una determinación más precisa de\(C\) y\(A\) para una respuesta más realista. Además, la densidad del aire varía a lo largo del camino.
Problemas de mezcla
PROBLEMAS DE MEZCLA A MENUDES SE PRODUCE EN UN PRIMER CURSO Sobre ecuaciones diferenciales En tales problemas consideramos un tanque de salmuera, agua que contiene una cantidad específica de sal con agua pura entrando y saliendo la mezcla, o el flujo de un contaminante dentro o fuera de un lago. El objetivo es dictar la cantidad de sal, o contaminante, en algún momento posterior.
En general se tiene un caudal de cierta concentración de mezcla entrando en una región y una mezcla que sale de la región. El objetivo es determinar la cantidad de cosas que hay en la región en un momento dado. Esto se rige por la ecuación
Tasa de cambio de sustancia\(=\) Rate In\(-\) Rate Out.
A menudo no se dan las tarifas. A uno se le da generalmente información sobre la concentración y los caudales dentro y fuera del sistema. Si uno presta atención a la dimentsión y esboza la situación, entonces uno puede escribir esta ecuación de tasa como una ecuación diferencial de primer orden. Consideramos un ejemplo sencillo.
Un tanque de 50 galones de agua pura tiene una mezcla de salmuera con concentración de 2 libras por galón entrando a razón de 5 galones por minuto. [Ver Figura\(\PageIndex{1}\).] Al mismo tiempo, los contenidos bien mezclados drenan a razón de 5 galones por minuto. Encuentra la cantidad de sal en el tanque a la vez\(t .\) En todos esos problemas se supone que la solución está bien mezclada en cada instante del tiempo.
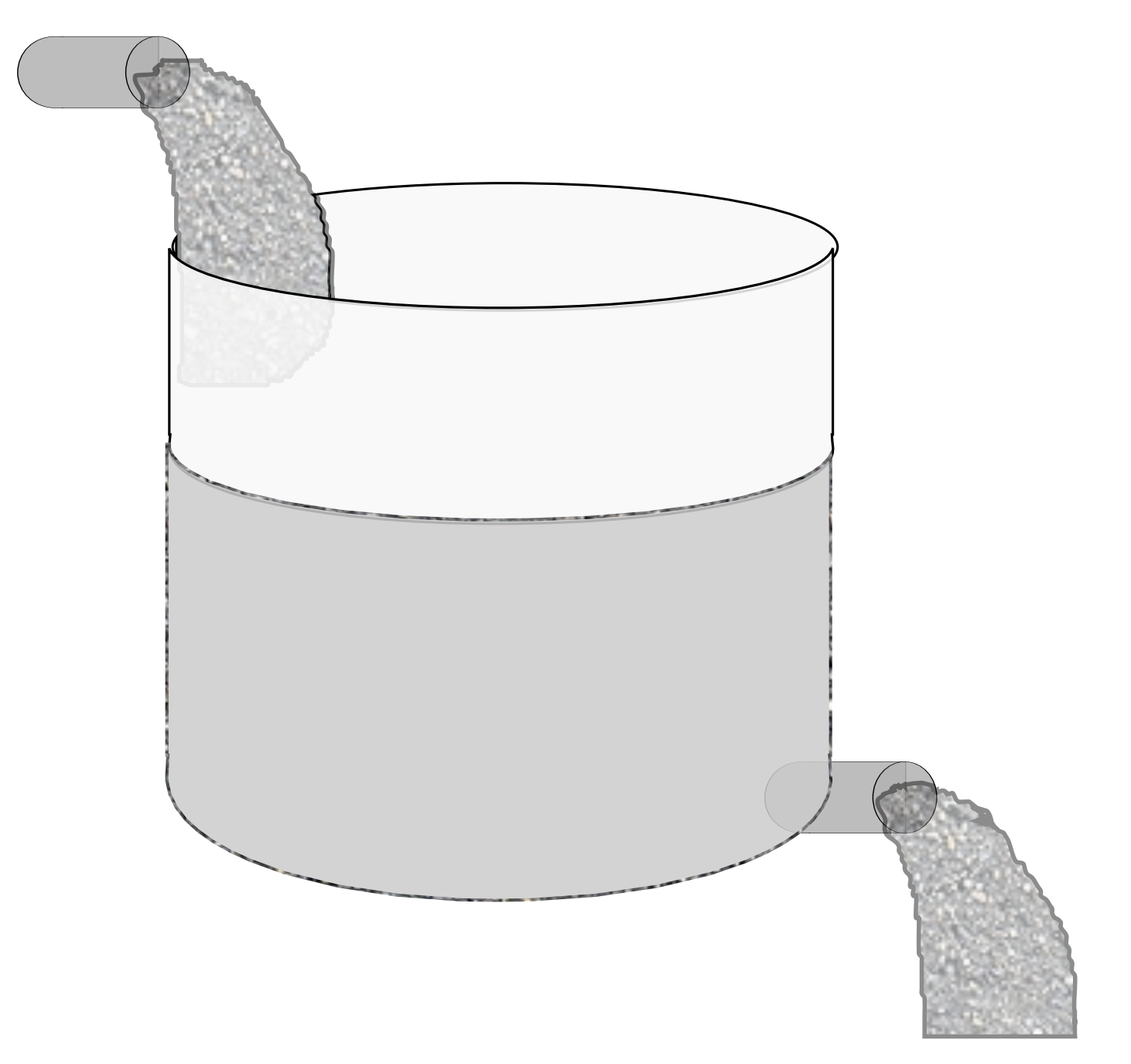
Dejar\(x(t)\) ser la cantidad de sal a la vez\(t\). Entonces la velocidad a la que aumenta la sal en el tanque se debe a la cantidad de sal que ingresa al tanque menos que la que sale del tanque. Para averiguar estas tarifas, se nota que\(d x / d t\) tiene unidades de libras por minuto. La cantidad de sal que entra por minuto viene dada por el producto de la concentración entrante multiplicada por la velocidad a la que entra la salmuera. Esto da las unidades correctas:
\(\left(2 \dfrac{\text { pounds }}{\text { gal }}\right)\left(5 \dfrac{\text { gal }}{\text { min }}\right)=10 \dfrac{\text { pounds }}{\text { min }} .\)
Del mismo modo, se puede determinar la tasa de salida como
\(\left(\dfrac{x \text { pounds }}{50 \text { gal }}\right)\left(5 \dfrac{\text { gal }}{\text { min }}\right)=\dfrac{x}{10} \dfrac{\text { pounds }}{\text { min }} .\)
Por lo tanto, tenemos
\(\dfrac{d x}{d t}=10-\dfrac{x}{10}\)
Esta ecuación se resuelve utilizando los métodos para ecuaciones lineales de primer orden. El factor integrador es\(\mu=e^{x / 10}\), lo que lleva a la solución general
\(x(t)=100+A e^{-t / 10}\)
Usando la condición inicial, uno encuentra la solución particular
\(x(t)=100\left(1-e^{-t / 10}\right)\)
A menudo uno está interesado en el comportamiento a largo plazo de un sistema. En este caso tenemos eso\(\lim _{t \rightarrow \infty} x(t)=100 \mathrm{lb}\). Esto tiene sentido porque 2 libras por galón entran durante este tiempo para eventualmente dejar los 50 galones enteros con esta concentración. Por lo tanto,
\(50 \mathrm{gal} \times 2 \dfrac{\mathrm{lb}}{50 \mathrm{gal}}=100 \mathrm{lb}\)
Trayectorias ortogonales de curvas
HAY MUCHOS PROBLEMAS DE LA GEOMETRÍA que han llevado al estudio de ecuaciones Uno de esos problemas es la construcción de trayectorias ortogonales. Dar una familia de curvas,\(y_{1}(x ; a)\), buscamos otra familia de curvas\(y_{2}(x ; c)\) tal que la segunda familia de curvas sean perpendiculares a la familia dada. Esto significa que las tangentes de dos curvas que se cruzan en el punto de intersección son perpendiculares entre sí. Las pendientes de las líneas tangentes vienen dadas por las derivadas\(y_{1}^{\prime}(x)\) y\(y_{2}^{\prime}(x)\). Recordamos de la geometría elemental que las pendientes de dos líneas perpendiculares están relacionadas por
\(y_{2}^{\prime}(x)=-\dfrac{1}{y_{1}^{\prime}(x)}\)
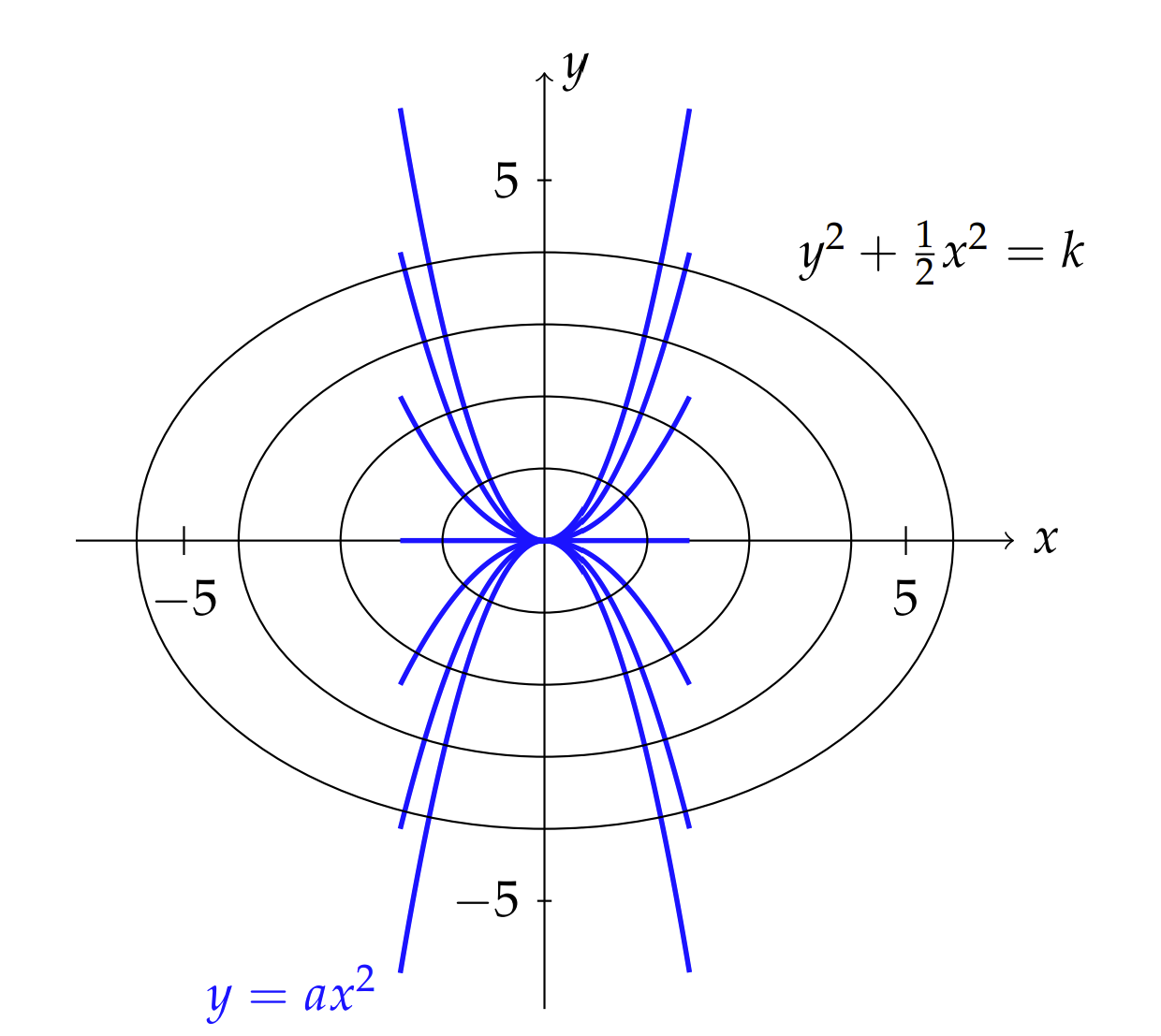
Encontrar una familia de trayectorias ortogonales a la familia de las parabolas\(y_{1}(x ; a)=a x^{2}\).
Observamos que la nueva colección de curvas tiene que satisfacer la ecuación
\[y_{2}^{\prime}(x)=-\dfrac{1}{y_{1}^{\prime}(x)}=-\dfrac{1}{2 a x} \nonumber \]
Antes de resolver para\(y_{2}(x)\), necesitamos eliminar el parámetro\(a\). De la función de dar, tenemos eso\(a=\dfrac{y}{x^{2}}\). Insertando esto en la ecuación para\(y_{2}^{\prime}\), tenemos
\[y^{\prime}(x)=-\dfrac{1}{2 a x}=-\dfrac{x}{2 y}\nonumber \]
Así, para encontrar\(y_{2}(x)\), tenemos que resolver la ecuación diferencial
\[2 y y^{\prime}+x=0\nonumber \]
Observando que\(\left(y^{2}\right)^{\prime}=2 y y^{\prime}\) y\(\left(\dfrac{1}{2} x^{2}\right)^{\prime}=x_{\prime \prime}\) esta ecuación (exacta) puede escribirse como
\[\dfrac{d}{d x}\left(y^{2}+\dfrac{1}{2} x^{2}\right)=0\nonumber \]
Integrando, encontramos la familia de soluciones,
\[y^{2}+\dfrac{1}{2} x^{2}=k \nonumber \]
En la Figura\(\PageIndex{2}\) trazamos ambas familias de curvas ortogonales.
Curvas de Persecución*
OTRA APLICACIÓN QUE ES INTERESANTE ES ENCONTRAR el camino que un cuerpo traza a medida que se mueve hacia un punto fijo u otro cuerpo en movimiento. Tales maldiciones se conocen como curvas de persecución. Estos podrían modelar aviones o submarinos siguiendo objetivos, o depredadores siguiendo presas. Esto lo demostramos con un ejemplo.
Un halcón en un punto\((x, y)\) ve a un gorrión viajando a velocidad a\(v\) lo largo de una línea recta. El halcón vuela hacia el gorrión a velocidad constante\(w\) pero siempre en una dirección a lo largo de la línea de visión entre sus posiciones. Si el halcón comienza en el punto\((a, 0)\) en\(t=0\), cuando está el gorrión\((0,0)\), entonces ¿cuál es el camino que debe seguir el halcón? ¿El halcón atrapará al gorrión? La situación se muestra en la Figura 1.6. Escogemos el camino del gorrión para estar a lo largo del\(y\) eje. Por lo tanto, el gorrión está en posición\((0, v t)\).
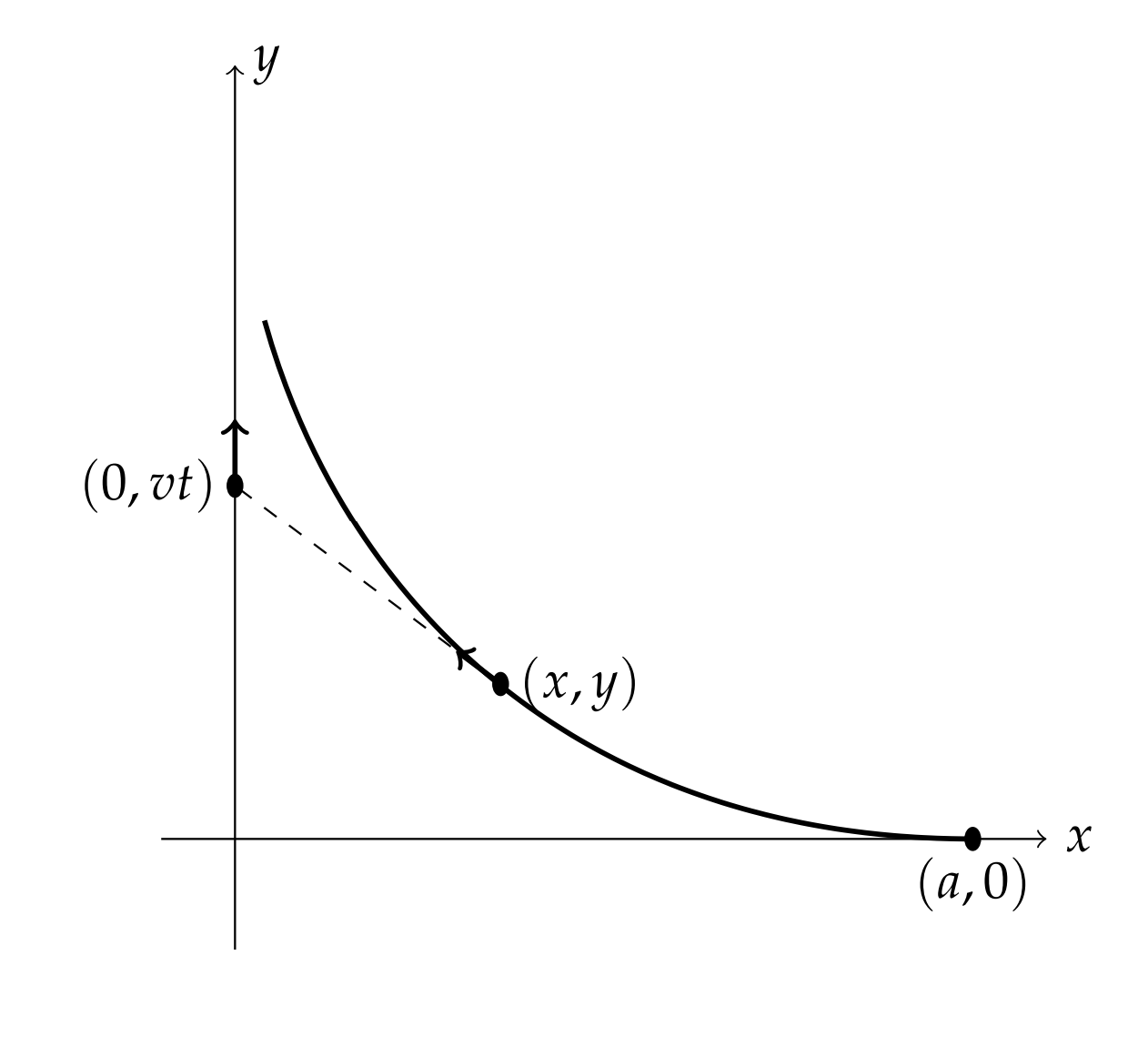
Primero necesitamos la ecuación de la línea de visión entre los puntos\((x, y)\) y\((0, v t)\). Considerando que la pendiente de la línea es la misma que la pendiente de la tangente al camino\(y=y(x)\),, tenemos
\(y^{\prime}=\dfrac{y-v t}{x}\)
El halcón se mueve a una velocidad constante, w. ya que la velocidad está relacionada con el tiempo a través de la distancia que recorre el halcón. Necesitamos encontrar la longitud del arcleight del camino entre\((a, 0)\) y\((x, y)\). Esto viene dado por
\(L=\int d s=\int_{x}^{a} \sqrt{1+\left[y^{\prime}(x)\right]^{2}} d x .\)
La distancia está relacionada con la velocidad,\(w\), y el tiempo,\(t\), por\(L=w t\). Eliminando el tiempo usando\(y^{\prime}=\dfrac{y-v t}{x}\), tenemos
\(\int_{x}^{a} \sqrt{1+\left[y^{\prime}(x)\right]^{2}} d x=\dfrac{w}{v}\left(y-x y^{\prime}\right)\)
Además, podemos diferenciar este resultado con respecto\(x\) a deshacerse de lo integral,
\(\sqrt{1+\left[y^{\prime}(x)\right]^{2}}=\dfrac{w}{v} x y^{\prime \prime}\)
Aunque esta es una ecuación diferencial de segundo orden para\(y(x)\), es una ecuación separable de primer orden en la función de velocidad\(z(x)=y^{\prime}(x)\). A saber,
\(\dfrac{w}{v} x z^{\prime}=\sqrt{1+z^{2}}\)
Separando variables, encontramos
\(\dfrac{w}{v} \int \dfrac{d z}{\sqrt{1+z^{2}}}=\int \dfrac{d x}{x}\)
Las integrales se pueden calcular utilizando métodos estándar a partir del cálculo. Podemos integrar fácilmente el lado derecho,
\(\int \dfrac{d x}{x}=\ln |x|+c_{1} .\)
El lado izquierdo requiere un poco de trabajo extra, o buscar el valor en Tablas o usar un paquete CAS. Recordemos que una sustitución trigonométrica está en orden. [Ver el Apéndice.] Dejamos\(z=\tan \theta .\) Entonces\(d z=\sec ^{2} \theta d \theta\). Los métodos proceden de la siguiente manera:
\[ \begin{aligned} \int \dfrac{d z}{\sqrt{1+z^{2}}}&=\int \dfrac{\sec ^{2} \theta}{\sqrt{1+\tan ^{2} \theta}} d \theta \\\ &=\int \sec \theta d \theta \\ &=\ln (\tan \theta+\sec \theta)+c_{2} \\ &=\ln \left(z+\sqrt{1+z^{2}}\right)+c_{2} \end{aligned}\label{1.44} \]
Armando estos, tenemos para\(x>0\),
\(\ln \left(z+\sqrt{1+z^{2}}\right)=\dfrac{v}{w} \ln x+C\)
Usando la condición inicial\(z=y^{\prime}=0\) y\(x=a\) en\(t=0\),
\(0=\dfrac{v}{w} \ln a+C\)
o\(C=-\dfrac{v}{w} \ln a\).
Usando este valor para\(c\), encontramos
\[ \begin{aligned} \ln \left(z+\sqrt{1+z^{2}}\right) &=\dfrac{v}{w} \ln x-\dfrac{v}{w} \ln a \\ \ln \left(z+\sqrt{1+z^{2}}\right) &=\dfrac{v}{w} \ln \dfrac{x}{a} \\ \ln \left(z+\sqrt{1+z^{2}}\right) &=\ln \left(\dfrac{x}{a}\right)^{\dfrac{v}{w}} \\ z+\sqrt{1+z^{2}} &=\left(\dfrac{x}{a}\right)^{\dfrac{v}{w}} \end{aligned} \nonumber \]
Podemos resolver para\(z=y^{\prime}\), para encontrar
\(y^{\prime}=\dfrac{1}{2}\left[\left(\dfrac{x}{a}\right)^{\dfrac{v}{w}}-\left(\dfrac{x}{a}\right)^{-\dfrac{v}{w}}\right]\)
Integrando,
\(y(x)=\dfrac{a}{2}\left[\dfrac{\left(\dfrac{x}{a}\right)^{1+\dfrac{v}{w}}}{1+\dfrac{v}{w}}-\dfrac{\left(\dfrac{x}{a}\right)^{1-\dfrac{v}{w}}}{1-\dfrac{v}{w}}\right]+k\)
La constante de integración\(k\),, se puede encontrar sabiendo\(y(a)=0 .\) Esto da
\[ \begin{aligned} 0 &=\dfrac{a}{2}\left[\dfrac{1}{1+\dfrac{v}{w}}-\dfrac{1}{1-\dfrac{v}{w}}\right]+k \\ k &=\dfrac{a}{2}\left[\dfrac{1}{1-\dfrac{v}{w}}-\dfrac{1}{1+\dfrac{v}{w}}\right] \\ &=\dfrac{a v w}{w^{2}-v^{2}} \end{aligned}\label{1.46} \]
La solución completa para el camino viene dada por
\(y(x)=\dfrac{a}{2}\left[\dfrac{\left(\dfrac{x}{a}\right)^{1+\dfrac{v}{w}}}{1+\dfrac{v}{w}}-\dfrac{\left(\dfrac{x}{a}\right)^{1-\dfrac{v}{w}}}{1-\dfrac{v}{w}}\right]+\dfrac{a v w}{w^{2}-v^{2}}\)
¿Puede el halcón atrapar al gorrión? Esto sucedería si hay un momento en que\(y(0)=v t\). \(x=0\)Insertando en la solución, tenemos\(y(0)=\dfrac{a v w}{w^{2}-v^{2}}=v t .\) Esto es posible si\(w>v .\)


