1.4: Otras ecuaciones de primer orden

Existen varias ecuaciones no lineales de primer orden cuya solución se puede obtener utilizando técnicas especiales. Concluimos este capítulo observando algunas de estas ecuaciones que llevan el nombre de famosos matemáticos del siglo\(17-18\) XX inspirados en diversas aplicaciones.

Ecuación de Bernoulli

Los Bernoulli eran una familia de matemáticos suizos que abarcaban tres generaciones. Todo comenzó con Jacob Bernoulli (1654-1705) y su hermano Johann Bernoulli (1667-1748). Jacob tuvo un hijo, Nicolás Bernoulli (1687- 1759) y Johann (1667-1748) tuvieron tres hijos, Nicolás Bernoulli II (1695-1726), Daniel Bernoulli (1700-1872) y Johann Bernoulli II (1710-1790). La última generación estuvo conformada por los hijos de Johann II, Johann Bernoulli III (1747-1807) y Jacob Bernoulli II (1759-1789). Johann, Jacob y Daniel Bernoulli fueron los más famosos de los Bernoulli. Jacob estudió con Leibniz, Johann estudió con su hermano mayor y posteriormente enseñó a Leonhard Euler (1707-1783) y Daniel Bernoulli, quien es conocido por su trabajo en hidrodinámica.

Comenzamos con la ecuación de Bernoulli, que lleva el nombre de Jacob Bernoulli (1655-1705). La ecuación de Bernoulli es de la forma

\(\dfrac{d y}{d x}+p(x) y=q(x) y^{n}, \quad n \neq 0,1\)

Tenga en cuenta que cuando\(n=0,1\) la ecuación es lineal y se puede resolver usando un factor integrador. La clave para resolver esta ecuación es usar la transformada\(z(x)=\dfrac{1}{y^{n-1}(x)}\) para hacer la ecuación para\(z(x)\) lineal. Demostramos el procedimiento usando un ejemplo.

Ejemplo\(\PageIndex{1}\)

Resolver la ecuación de Bernoulli\(x y^{\prime}+y=y^{2} \ln x\) para\(x>0\). En este ejemplo\(p(x)=1, q(x)=\ln x\), y\(n=2\). Por lo tanto, dejamos mous de los Bernoulli's. Jacob estudió\(z=\dfrac{1}{y} .\) Entonces,

\(z^{\prime}=-\dfrac{1}{y^{2}} y^{\prime}=z^{2} y^{\prime} .\)

Insertando\(z=y^{-1}\) y\(z^{\prime}=z^{2} y^{\prime}\) en la ecuación diferencial, tenemos

\[ \begin{aligned} x y^{\prime}+y &=y^{2} \ln x \\ -x \dfrac{z^{\prime}}{z^{2}}+\dfrac{1}{z} &=\dfrac{\ln x}{z^{2}} \\ -x z^{\prime}+z &=\ln x \\ z^{\prime}-\dfrac{1}{x} z=-\dfrac{\ln x}{x} . \end{aligned} \end{equation}\label{1.47} \]

Así, la ecuación resultante es una ecuación diferencial lineal de primer orden. Se puede resolver utilizando el factor integrador,

\(\mu(x)=\exp \left(-\int \dfrac{d x}{x}\right)=\dfrac{1}{x}\)

Multiplicando la ecuación diferencial por el factor integrador, tenemos

\(\left(\dfrac{z}{x}\right)^{\prime}=\dfrac{\ln x}{x^{2}}\)

Integrando, obtenemos

\[ \begin{aligned} \dfrac{z}{x} &=-\int \dfrac{\ln x}{x^{2}}+C \\ &=\dfrac{\ln x}{x}+\int \dfrac{d x}{x^{2}}+C \\ &=\dfrac{\ln x}{x}+\dfrac{1}{x}+C \end{aligned}\label{1.48} \]

Multiplicando por\(x\), tenemos\(z=\ln x+1+C x .\) Desde\(z=y^{-1}\), la solución general al problema es

\(y=\dfrac{1}{\ln x+1+C x}\)

Ecuaciones de Lagrange y Clairaut

ALEXIS CLAUDE CLAIRAUT (1713-1765) SOLUCIONÓ la ecuación diferencial

\(y=x y^{\prime}+g\left(y^{\prime}\right)\)

Este es un caso especial de la familia de ecuaciones de Lagrange,

\(y=x f\left(y^{\prime}\right)+g\left(y^{\prime}\right)\)

llamado así por Joseph Louis Lagrange (1736-1813). Estas ecuaciones también tienen soluciones llamadas soluciones singulares. Soluciones singulares son soluciones para las que existe una falla de singularidad al problema de valor inicial en cada punto de la curva. Una solución singular es a menudo una que es tangente a cada solución en una familia de soluciones.

Primero, consideramos resolver la ecuación más general de Lagrange. Dejemos\(p=y^{\prime}\) en la ecuación de Lagrange, dando

\[y=x f(p)+g(p) \nonumber \]

A continuación, nos diferenciamos con respecto\(x\) a encontrar

\(y^{\prime}=p=f(p)+x f^{\prime}(p) p^{\prime}+g^{\prime}(p) p^{\prime}\)

Ecuaciones de Lagrange,\(y=x f\left(y^{\prime}\right)+g\left(y^{\prime}\right)\).

Aquí usamos la Regla de la Cadena. Por ejemplo,

\(\dfrac{d g(p)}{d x}=\dfrac{d g}{d p} \dfrac{d p}{d x}\)

Resolviendo para\(p^{\prime}\), tenemos

\[\dfrac{d p}{d x}=\dfrac{p-f(p)}{x f^{\prime}(p)+g^{\prime}(p)} \nonumber \]

Hemos introducido\(p=p(x)\), visto como una función de\(x\). Supongamos que podemos invertir esta función para encontrar\(x=x(p)\). Entonces, a partir del cálculo introductorio, sabemos que las derivadas de una función y su inversa están relacionadas,

\(\dfrac{d x}{d p}=\dfrac{1}{\dfrac{d p}{d x}}\)

Aplicando esto a la ecuación\(\PageIndex{4}\), tenemos

\[ \begin{aligned} \dfrac{d x}{d p} &=\dfrac{x f^{\prime}(p)+g^{\prime}(p)}{p-f(p)} \\ x^{\prime}-\dfrac{f^{\prime}(p)}{p-f(p)} x &=\dfrac{g^{\prime}(p)}{p-f(p)} \end{aligned} \label{1.51} \]

asumiendo que\(p-f(p) \neq 0\).

Como se puede ver, hemos transformado la ecuación de Lagrange en una ecuación diferencial lineal de primer orden\(\PageIndex{5}\) para\(x(p)\). Usando métodos anteriores en el capítulo, podemos en principio obtener una familia de soluciones

\(x=F(p, C)\)

donde\(C\) es una constante de integración arbitraria. Usando Ecuación\(\PageIndex{3}\), uno podría ser capaz de eliminar\(p\) en Ecuación\(\PageIndex{5}\) para obtener una familia de soluciones de la ecuación de Lagrange en la forma

\(\varphi(x, y, C)=0\)

Si no es posible eliminar\(p\) de Ecuaciones\(\PageIndex{3}\) y\(\PageIndex{5}\), entonces se podría reportar la familia de soluciones como una familia paramétrica de soluciones con\(p\) el parámetro. Entonces, las soluciones paramétricas tomarían la forma

\[ \begin{aligned} &x=F(p, C) \\ &y=F(p, C) f(p)+g(p) \end{aligned} \label{1.52} \]

Las soluciones singulares son posibles para las ecuaciones de Lagrange.

También habíamos asumido el\(p-f(p) \neq 0\). Sin embargo, también podría haber soluciones de la ecuación de Lagrange para las cuales\(p-f(p)=0 .\) Tales soluciones se denominan soluciones singulares.

Ejemplo\(\PageIndex{2}\)

Resolver la ecuación de Lagrange\(y=2 x y^{\prime}-y^{\prime 2}\).

Empezaremos con Ecuación\(\PageIndex{5}\). Señalando que\(f(p)=2 p, g(p)=\)\(-p^{2}\), tenemos

\ [\ begin {alineado}
x^ {\ prime} -\ dfrac {f^ {\ prime} (p)} {p-f (p)} x &=\ dfrac {g^ {\ prime} (p)} {p-f (p)}\
x^ {\ prime} -\ dfrac {2} {p-2 p} x &=\ dfrac {-2 p} p-2 p}\\
x^ {\ prime} +\ dfrac {2} {p} x &=2.
\ end {alineado}\ etiqueta {1.53}\]

Figura\(\PageIndex{1}\): Familia de soluciones de la ecuación LA-Grange\(y=2 x y^{\prime}-y^{\prime 2}\)

Esta ecuación diferencial lineal de primer orden se puede resolver utilizando un factor integrador. A saber,

\(\mu(p)=\exp \left(\int \dfrac{2}{p} dp\right)=e^{2 \ln p}=p^{2}\)

Multiplicando la ecuación diferencial por el factor integrador, tenemos

\(\dfrac{d}{d p}\left(x p^{2}\right)=2 p^{2}\)

Integrando,

\(x p^{2}=\dfrac{2}{3} p^{3}+C.\)

Esto da la solución general

\(x(p)=\dfrac{2}{3} p+\dfrac{C}{p^{2}}\)

Sustituyendo\(y^{\prime}=p\) en la ecuación diferencial original, tenemos\(y=2 x p-p^{2}\). La familia de soluciones viene dada por las ecuaciones paramétricas

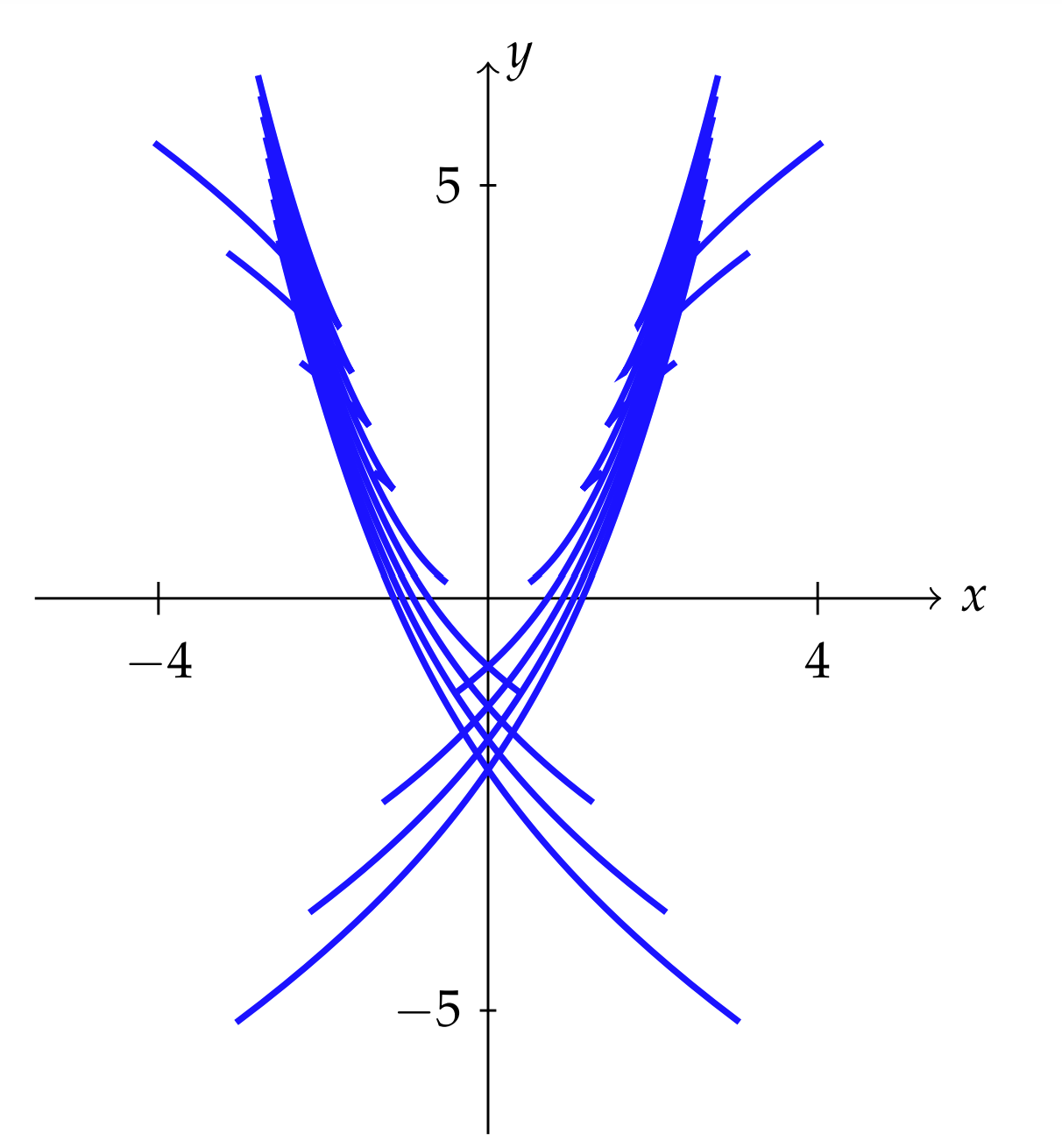
\[\begin{aligned} x &=\dfrac{2}{3} p+\dfrac{C}{p^{2}}, \\ y &=2\left(\dfrac{2}{3} p+\dfrac{C}{p^{2}}\right) p-p^{2} \\ &=\dfrac{1}{3} p^{2}+\dfrac{2 C}{p} . \end{aligned} \label{1.54} \]

Las gráficas de estas soluciones se muestran en la Figura\(\PageIndex{1}\).

También tenemos que verificar si hay una solución singular. Resolvemos la ecuación\(p-f(p)=0\), o\(p=0 .\) Esto da la solución\(y(x)=\left(2 x p-p^{2}\right) p=0=0 .\)

La ecuación diferencial de Clairaut viene dada por

\(y=x y^{\prime}+g\left(y^{\prime}\right)\)

Dejando\(p=y^{\prime}\), tenemos

\(y=x p+g(p)\)

Esta es la ecuación de Lagrange con\(f(p)=p\). Diferenciando con respecto a x,

Ecuaciones de Clairaut,\(y=x y^{\prime}+g\left(y^{\prime}\right)\).

\(p=p+x p^{\prime}+g^{\prime}(p) p^{\prime}\)

Reordenando, encontramos

\(x=-g^{\prime}(p)\)

Entonces, tenemos la solución paramétrica

\[ \begin{aligned} &x=-g^{\prime}(p) \\ &y=-p g^{\prime}(p)+g(p) \end{aligned} \label{1.55} \]

Para el caso de que\(y^{\prime}=C\), se puede ver que\(y=C x+g(C)\) es una solución general de solución.

Ejemplo\(\PageIndex{3}\)

Encuentra las soluciones de\(y=x y^{\prime}-y^{\prime 2}\).

Como se señaló, existe una familia de soluciones en línea recta\(y=C x-C^{2}\), ya que\(g(p)=-p^{2}\). También podría por una solución paramétrica no contener\(n\) esta familia. Estaría dado por el conjunto de ecuaciones

\[ \begin{aligned} &x=-g^{\prime}(p)=2 p \\ &y=-p g^{\prime}(p)+g(p)=2 p^{2}-p^{2}=p^{2} \end{aligned} \label{1.56} \]

Figura\(\PageIndex{2}\): Gráfica de soluciones a la ecuación de Clairaut\(y=x y^{\prime}-y^{\prime 2}\). Las soluciones de línea recta son una familia de curvas cuyo límite es la solución paramétrica.

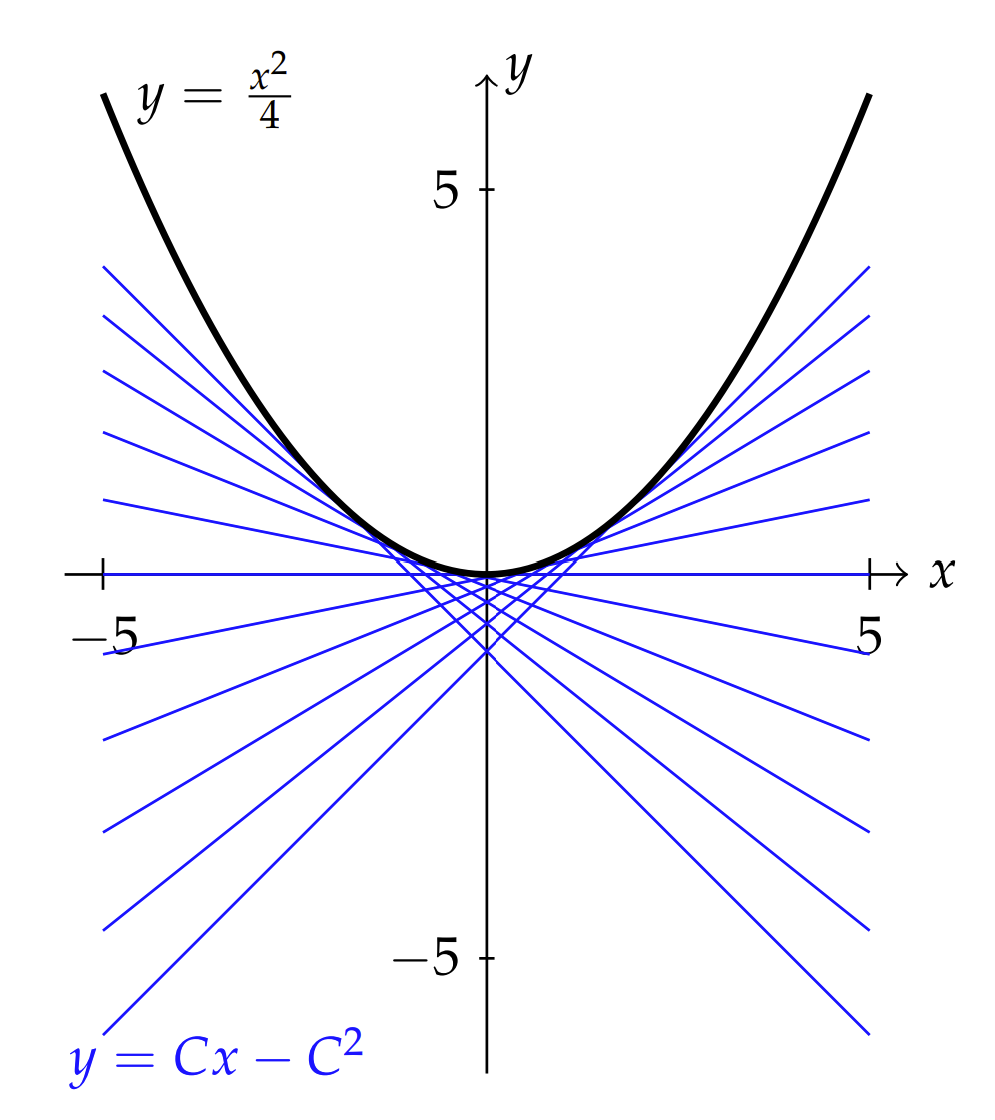
Eliminando\(p\), tenemos la curva parabólica\(y=x^{2} / 4\).

En la Figura\(\PageIndex{2}\) trazamos estas soluciones. La familia de
luciones de línea recta se muestra en azul. La curva limitante trazada, al igual que las figuras de cadena que uno podría crear, es la curva paramétrica.

Ecuación de Riccati

JACOPO FRANCESCO RICCATI (\(1676-1754\)) CURVAS ESTUDIADAS Con alguna curvatura Propuso una ecuación de la forma

\(y^{\prime}+a(x) y^{2}+b(x) y+c(x)=0\)

alrededor de 1720. Esto lo comunicó a los Bernoulli's, fue Daniel Bernoulli quien en realidad había resuelto esta ecuación. Como señaló Ranjan Roy\((2011)\), Riccati había publicado su ecuación en 1722 con una nota que D. Bernoulli daba la solución en términos de un anagrama. Además, cuando\(a \equiv 0\), la ecuación de Riccati se reduce a una ecuación de Bernoulli.

En la Sección 7.2, mostraremos que la ecuación de Ricatti puede transformarse en una ecuación diferencial lineal de segundo orden. Sin embargo, hay casos especiales en los que podemos tener en nuestras manos las soluciones. Por ejemplo, si\(a, b\), y\(c\) son constantes, entonces la ecuación diferencial se puede integrar directamente. Tenemos

\(\dfrac{d y}{d x}=-\left(a y^{2}+b y+c\right)\)

Esta ecuación es separable y obtenemos

\(x-C=-\int \dfrac{d y}{a y^{2}+b y+c}\)

Cuando se deja una ecuación diferencial en esta forma, se dice que se resuelve por cuadratura cuando la integral resultante en principio puede calcularse en términos de funciones elementales. \({ }^{1}\)

1

Por funciones elementales queremos decir

\[x-C=-\int \dfrac{d y}{a y^{2}+b y+c} \nonumber \]

funciones bien conocidas como polinomios, trigonométricos, hiperbólicos, y algunos no tan bien conocidos para los estudiantes universitarios, como Jacobi o Weierstrass funciones elípticas.

Si se conoce una solución en particular, entonces se puede obtener una solución a la ecuación de Riccati. Sea la solución conocida\(y_{1}(x)\) y suponga que la solución general toma la forma\(y(x)=y_{1}(x)+z(x)\) para alguna función desconocida\(z(x)\). Sustituyendo esta forma en la ecuación diferencial, podemos mostrar que\(v(x)=1 / z(x)\) satisface una ecuación diferencial lineal de primer orden.

\(y=y_{1}+z\)Insertando en la ecuación general de Riccati, tenemos

\[\begin{equation} \begin{aligned} 0=& \dfrac{d y}{d x}+a(x) y^{2}+b(x) y+c \\ =& \dfrac{d z}{d x}+a z^{2}+2 a z y_{1}+b z+\\ &+\dfrac{d y_{1}}{d x}+a y_{1}^{2}+b y_{1}+c \\ =& \dfrac{d z}{d x}+a(x)\left[2 y_{1} z+z^{2}\right]+b(x) z \\ -a(x) z^{2}=& \dfrac{d z}{d x}+\left[2 a(x) y_{1}+b(x)\right] z . \end{aligned}\end{equation}\label{1.57} \]

La última ecuación es una ecuación de Bernoulli con\(n=2 .\) So, podemos convertirla en una ecuación lineal con la sustitución\(z=\dfrac{1}{v}, z^{\prime}=-\dfrac{z^{\prime}}{v^{2}}\). Entonces, obtenemos una ecuación diferencial para\(v(x)\). Está dado por

\(v^{\prime}-\left(2 a(x) y_{1}(x)+b(x)\right) v=a(x)\)

Ejemplo\(\PageIndex{4}\)

Encuentre la solución general de la ecuación de Riccati,\(y^{\prime}-\)\(y^{2}+2 e^{x} y-e^{2 x}-e^{x}=0\), usando la solución particular\(y_{1}(x)=e^{x} .\)

Dejamos que la solución buscada tome la forma\(y(x)=z(x)+e^{x}\). Entonces, la ecuación para\(z(x)\) se encuentra como

\(\dfrac{d z}{d x}=z^{2}\)

Esta ecuación es lo suficientemente simple como para integrarse directamente para obtener\(z=\dfrac{1}{C-x}\). Entonces, la solución al problema se convierte en

\(y(x)=\dfrac{1}{C-x}+e^{x}\)