2.3: Osciladores armónicos simples
- Page ID
- 119685
EL SIGUIENTE PROBLEMA FÍSICO DE INTERÉS es el del simple movimiento Tal movimiento surge en muchos lugares de la física y proporciona una primera aproximación genérica a los modelos de movimiento oscilatorio. Este es el comienzo de un hilo importante que se extiende a lo largo de este curso. Has visto movimiento armónico simple en tu clase introductoria de física. Revisaremos SHM (o SHO en algunos textos) observando resortes, péndula (el plural del\(m\) péndulo) y circuitos simples.
2.3.1: Sistemas Masa-Muelle
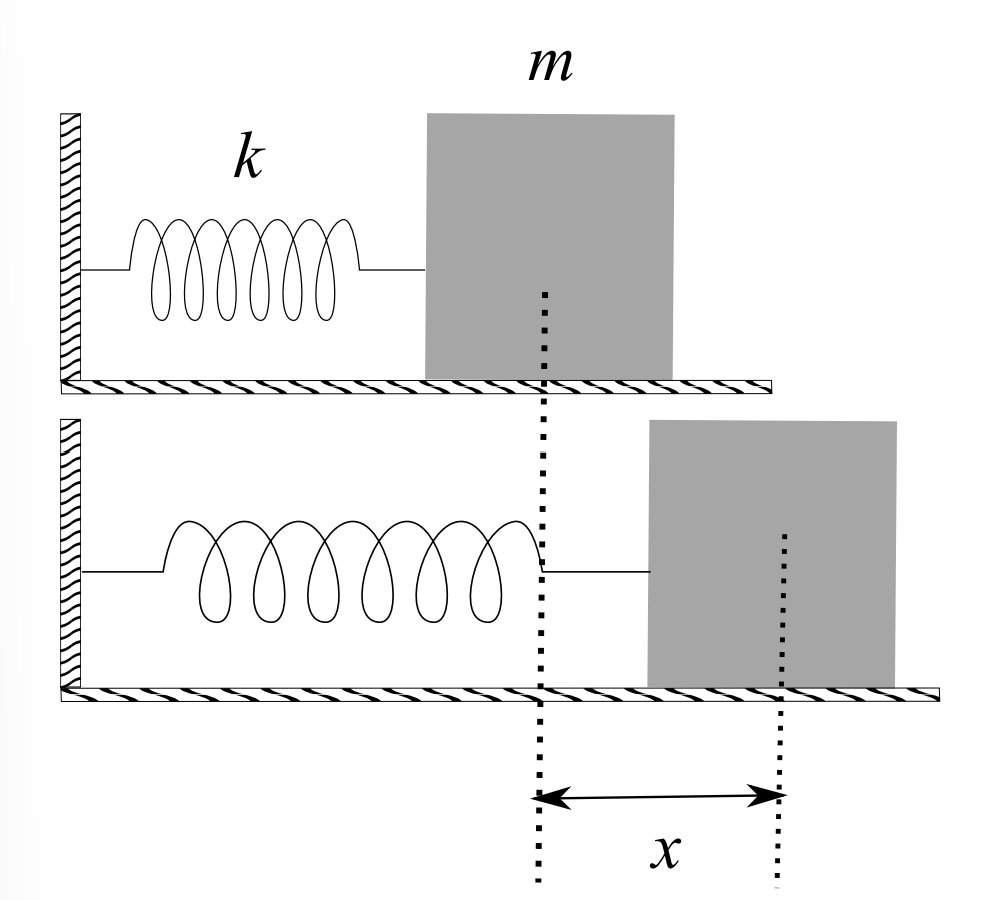
COMIENZAMOS CON EL CASO DE UN SOLO BLOQUE SOBRE UN MUELLE COMO SE\(\PageIndex{1}\) MU La fuerza neta en este caso es la fuerza restauradora de la primavera dada por la Ley de Hooke,
\(F_{s}=-k x\)
donde\(k>0\) esta la constante primaveral. Aquí\(x\) está el alargamiento, o desplazamiento del resorte desde el equilibrio. Cuando el desplazamiento es positivo, la fuerza del resorte es negativa y cuando el desplazamiento es negativo la fuerza del resorte es positiva. Hemos representado un sistema horizontal sentado sobre una superficie sin fricción. Se puede proporcionar un modelo similar para muelles orientados verticalmente. Sin embargo, es necesario tener en cuenta la gravedad para determinar la ubicación del equilibrio. De lo contrario, el movimiento oscilatorio sobre el equilibrio se modela de la misma manera.
De la Segunda Ley de Newton\(F=m \ddot{x}\),, obtenemos la ecuación para el movimiento de la masa en la primavera:
\[m \ddot{x}+k x=0 \label{2.19} \]
Dividiendo por la masa, esta ecuación se puede escribir en la forma
\[\ddot{x}+\omega^{2} x=0 \nonumber \]
donde
\(\omega=\sqrt{\dfrac{k}{m}}\)
Esta es la ecuación diferencial genérica para el movimiento armónico simple.
Posteriormente derivaremos soluciones de tales ecuaciones de manera metódica. Por ahora observamos que dos soluciones de esta ecuación están dadas por
\[ \begin{aligned} x(t) &=A \cos \omega t \\ x(t) &=A \sin \omega t \end{aligned} \label{2.21} \]
donde\(\omega\) es la frecuencia angular, medida en rad/s, y\(A\) se llama la amplitud de la oscilación.
La frecuencia angular está relacionada con la frecuencia por
\(\omega=2 \pi f\)
donde\(f\) se mide en ciclos por segundo, o Hertz. Además, esto está relacionado con el período de oscilación, el tiempo que tarda la masa en pasar por un ciclo:
\(T=1 / f\)
2.3.2: El Péndulo Simple
EL PENDULO SIMPLE consiste en una masa puntual\(m\) colgada de una cuerda de longitud\(L\) de algún soporte. [Ver Figura\(\PageIndex{2}\).] Uno tira de la masa hacia atrás a algún ángulo inicial\(\theta_{0}\),, y la libera. El objetivo es encontrar la posición angular en función del tiempo.
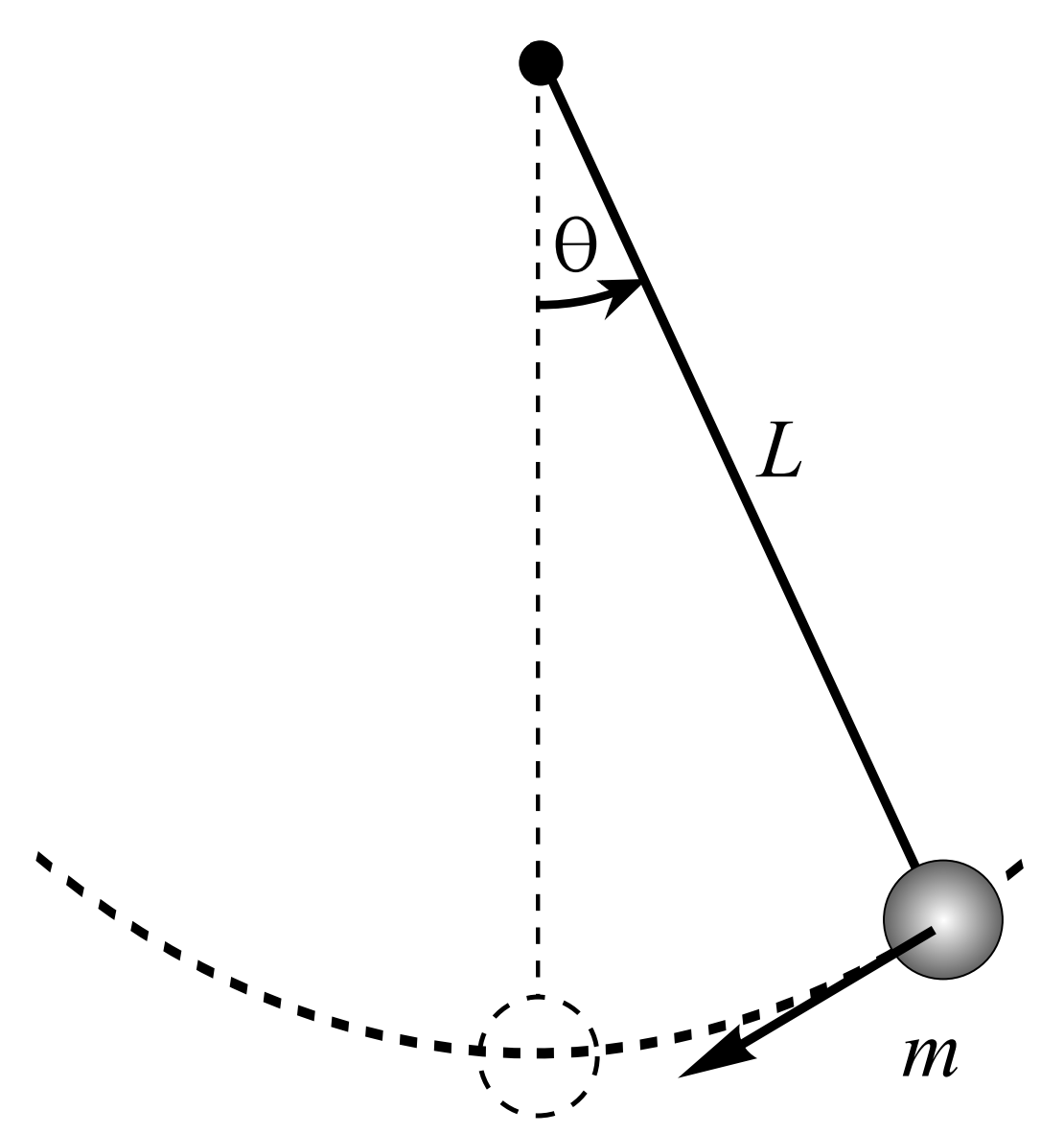
Hay un par de posibles derivaciones. Podríamos usar la Segunda Ley del Movimiento de Newton\(F=m a\), o su análogo rotacional en términos de torque,\(\tau=I \alpha\). Usaremos el primero solo para limitar la cantidad de antecedentes físicos necesarios.
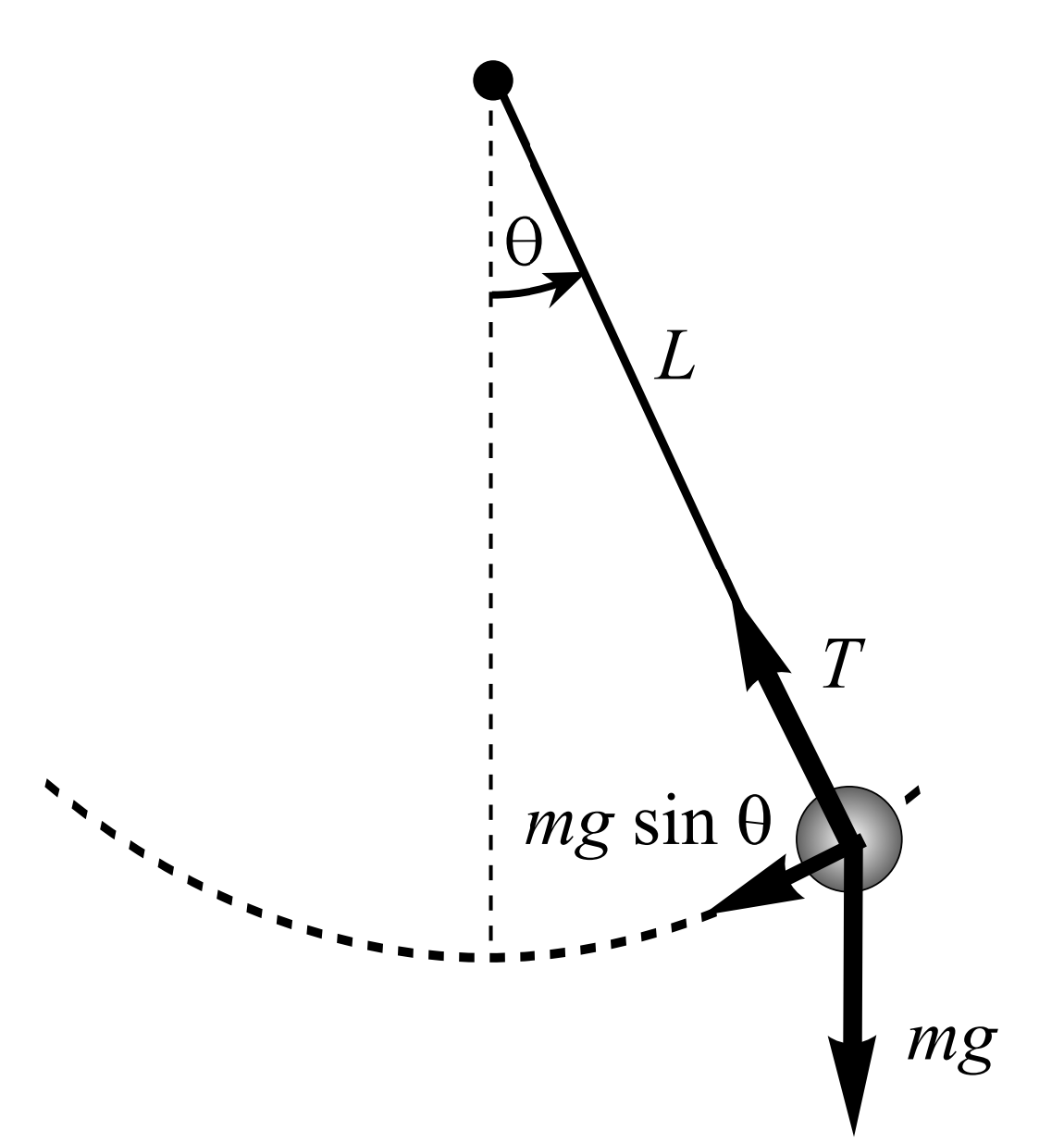
Hay dos fuerzas que actúan sobre la masa puntual. El primero es la gravedad. Esto apunta hacia abajo y tiene una magnitud de\(m g\), donde\(g\) está el símbolo estándar para la aceleración debido a la gravedad. La otra fuerza es la tensión en la cuerda. En la Figura\(\PageIndex{3}\) se muestran estas fuerzas y su suma. La magnitud de la suma se encuentra fácilmente\(F=m g \sin \theta\) usando la adición de estos dos vectores.
Ahora, la Segunda Ley del Movimiento de Newton nos dice que la fuerza neta es la masa multiplicada por la aceleración. Entonces, podemos escribir
\(m \ddot{x} = -mg \sin \theta \)
A continuación, necesitamos relacionarnos\(x\) y\(\theta . x\) es la distancia recorrida, que es la longitud del arco trazada por la masa puntual. La longitud del arco está relacionada con el ángulo, siempre que el ángulo se mida en radianes. A saber,\(x=r \theta\) para\(r=L\). Así, podemos escribir
\(m L \ddot{\theta}=-m g \sin \theta .\)
Ecuación de péndulo lineal y no lineal. Cancelando las masas, esto nos da entonces la ecuación del péndulo no lineal
\[L \ddot{\theta}+g \sin \theta=0 \nonumber \]
La ecuación para un péndulo compuesto toma una forma similar. Comenzamos con la forma rotacional de la segunda ley de Newton\(\tau=I \alpha\). Observando que el par debido a la gravedad actúa en la posición del centro de masa\(\ell\), se da el par
\[\ddot{\theta}+\omega^{2} \theta=0 \nonumber \]
por\(\tau=-m g \ell \sin \theta\). Ya que\(\alpha=\ddot{\theta}\), tenemos\(I \ddot{\theta}=-m g \ell \sin \theta\). Entonces, para ángulos pequeños\(\ddot{\theta}+\omega^{2} \theta=0\), dónde\(\omega=\dfrac{m g \ell}{I}\). Para un péndulo simple, dejamos\(\ell=L\) y\(I=m L^{2}\), y obtenemos\(\omega=\sqrt{g / L} .\)
Observamos que esta ecuación es de la misma forma que el sistema masa-resorte. Definimos\(\omega=\sqrt{g / L}\) y obtenemos la ecuación para el movimiento armónico simple,
\(\ddot{\theta}+\omega^{2} \theta=0\)
Existen varias variaciones de Ecuación las\(\PageIndex{4}\) cuales serán utilizadas en este texto. El primero es el péndulo lineal. Esto se obtiene haciendo una pequeña aproximación de ángulo. Para ángulos pequeños sabemos que\(\sin \theta \approx \theta .\) Bajo esta aproximación, la ecuación\(\PageIndex{4}\) se convierte
\[L \ddot{\theta}+g \theta=0 . \nonumber \]
2.3.3: Circuitos LRC
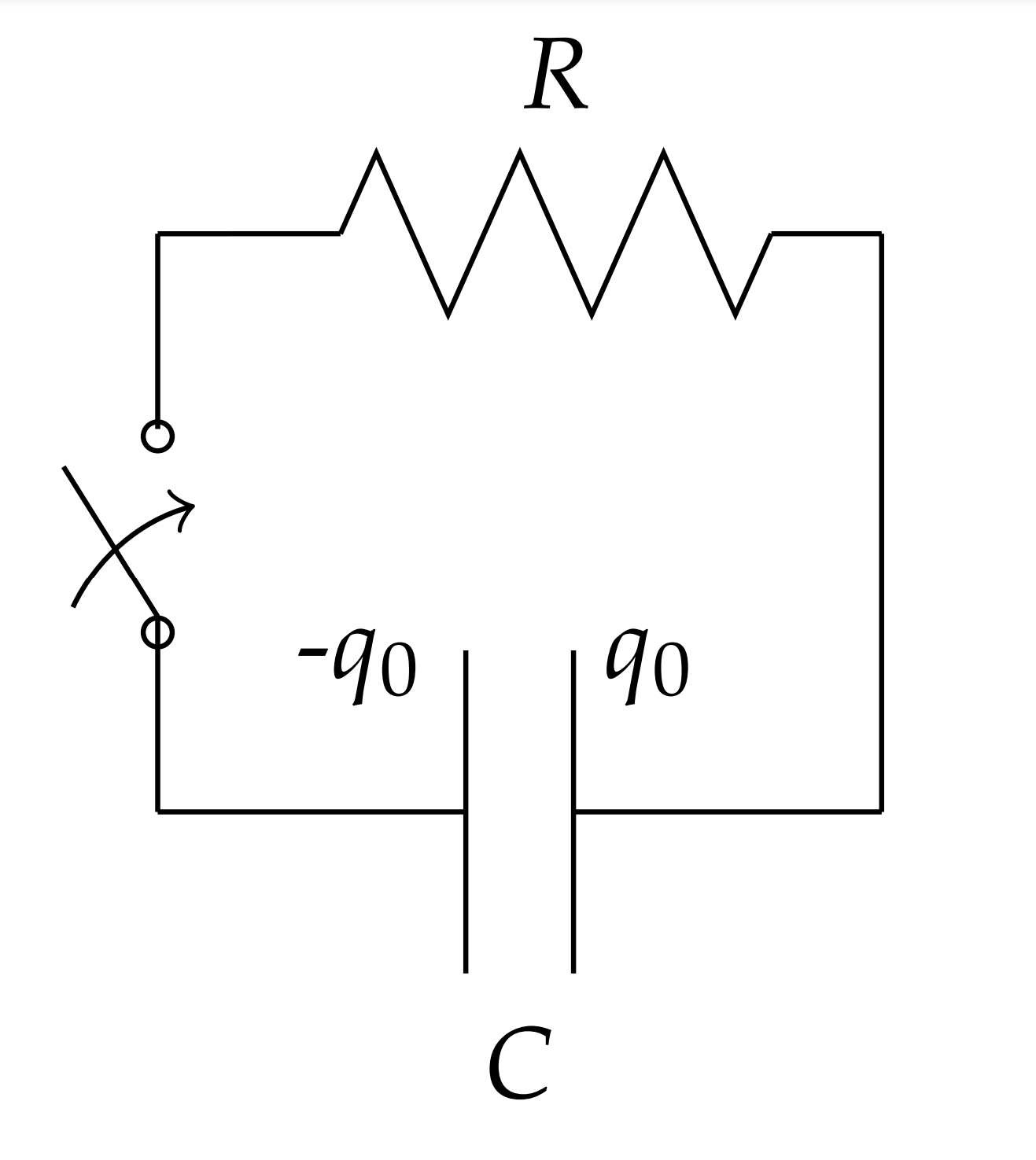
Otro problema típico que se encuentra a menudo en una clase de física de primer año es el de un circuito en serie LRC. Este circuito se representa en la Figura\(\PageIndex{4}\). La resistencia es un elemento de circuito que satisface la Ley de Ohm. El condensador es un dispositivo que almacena energía eléctrica y un inductor, o bobina, almacena energía magnética.
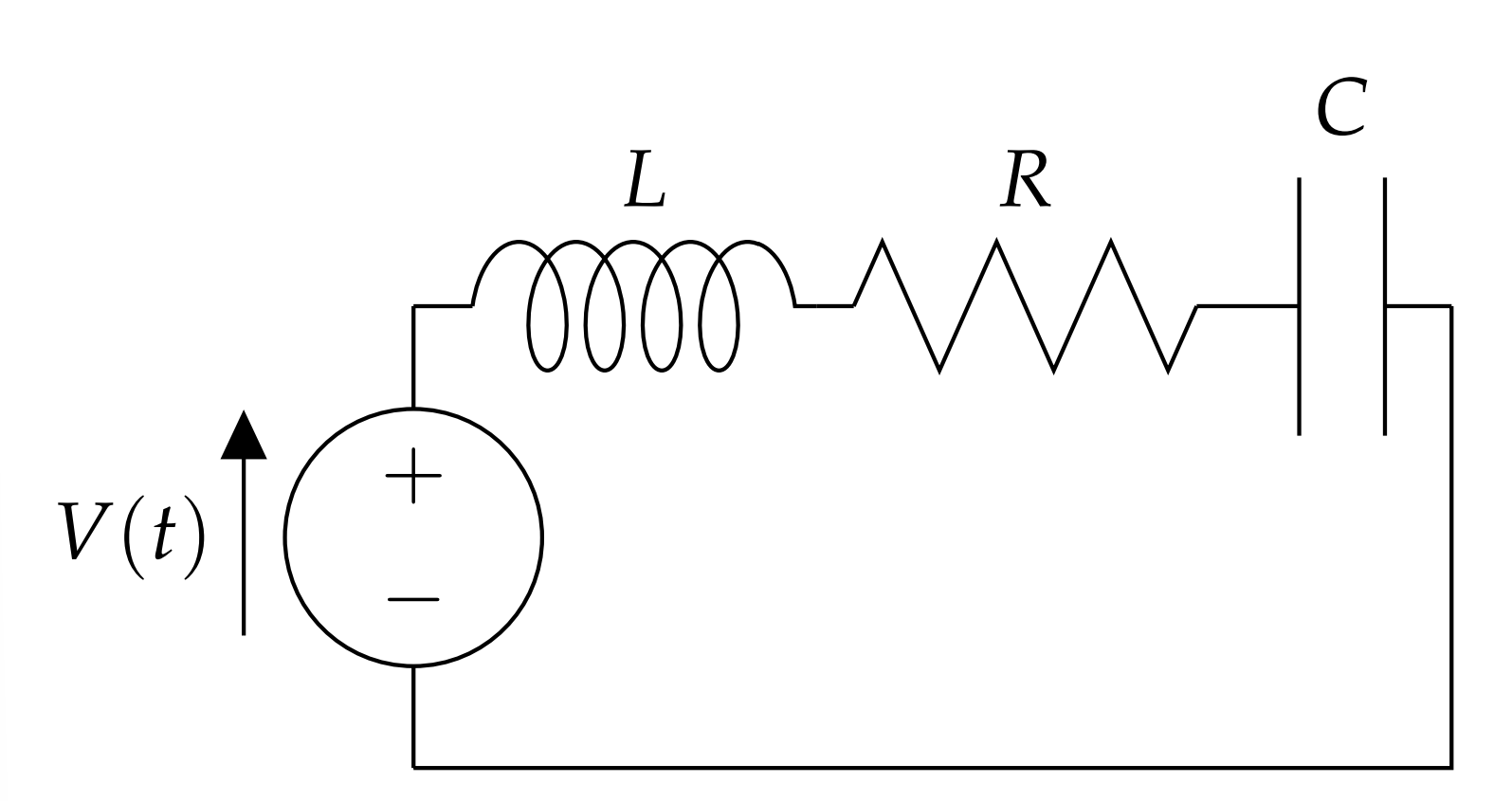
La física para este problema proviene de las Reglas para circuitos de Kirchoff. A saber, la suma de las caídas en el potencial eléctrico se establece igual a las subidas en el potencial eléctrico. Las caídas potenciales a través de cada elemento del circuito están dadas por
- Resistor:\(V=I R .\)
- Capacitor:\(V=\dfrac{q}{C} .\)
- Inductor:\(V=L \dfrac{d I}{d t} .\)
Además, necesitamos definir la corriente como\(I=\dfrac{d q}{d t} .\) dónde\(q\) está la carga en el circuito. Sumando estas caídas de potencial, las configuramos iguales a la tensión suministrada por la fuente de voltaje,\(V(t)\). Por lo tanto, obtenemos
\(I R+\dfrac{q}{C}+L \dfrac{d I}{d t}=V(t)\)
Ya que ambos\(q\) y\(I\) son desconocidos, podemos sustituir la corriente por su expresión en términos de la carga para obtener
\(L \ddot{q}+R \dot{q}+\dfrac{1}{C} q=V(t)\)
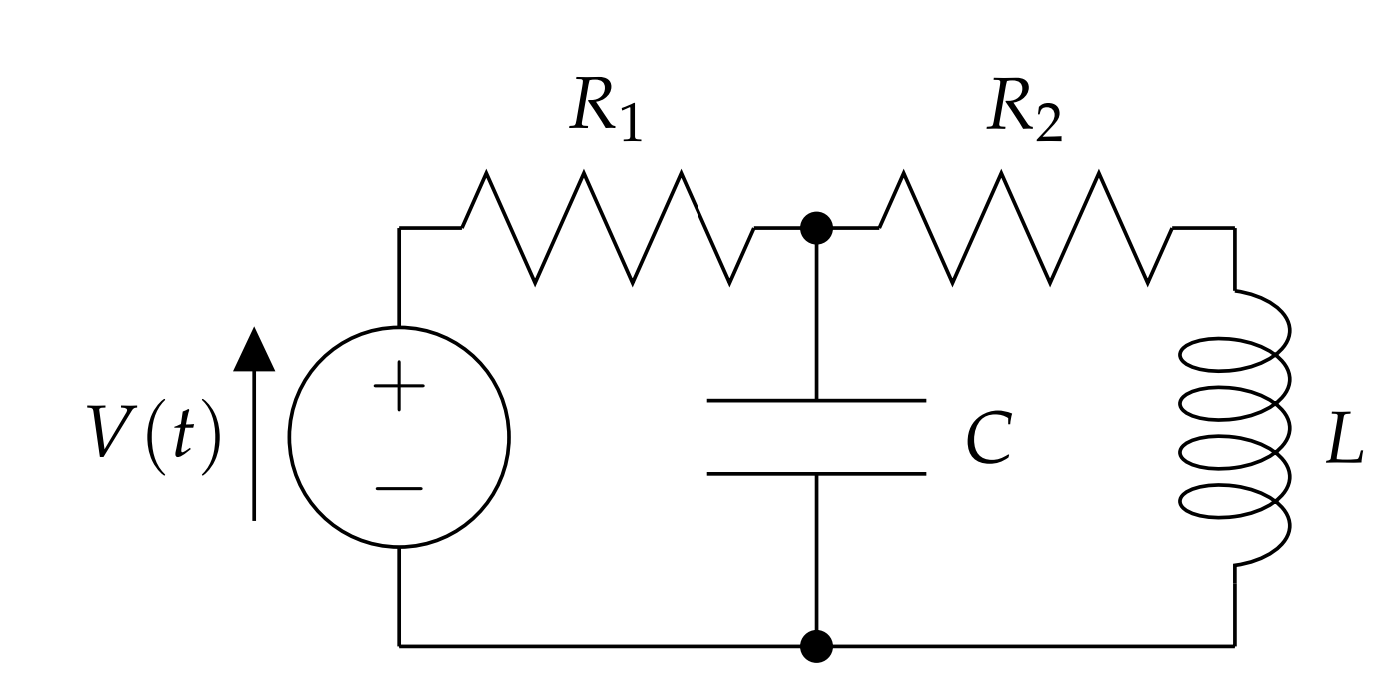
Esta es una ecuación de segundo orden para\(q(t)\). Los circuitos más complicados son posibles al observar conexiones en paralelo, u otras combinaciones, de resistencias, condensadores e inductores. Esto dará como resultado varias ecuaciones para cada bucle en el circuito, lo que conducirá a sistemas más grandes de ecuaciones diferenciales. Un ejemplo de otra configuración de circuito se muestra en la Figura\(\PageIndex{5}\). Esto no es un problema que pueda cubrirse en el curso de física de primer año. Se puede configurar un sistema de ecuaciones de segundo orden y proceder a resolverlas. Veremos cómo resolver este tipo de problemas en el próximo capítulo.
A continuación veremos casos especiales que surgen para la ecuación del circuito LRC en serie. Estos incluyen circuitos RC, solucionables por métodos de primer orden y circuitos LC, que conducen a un comportamiento oscilatorio.
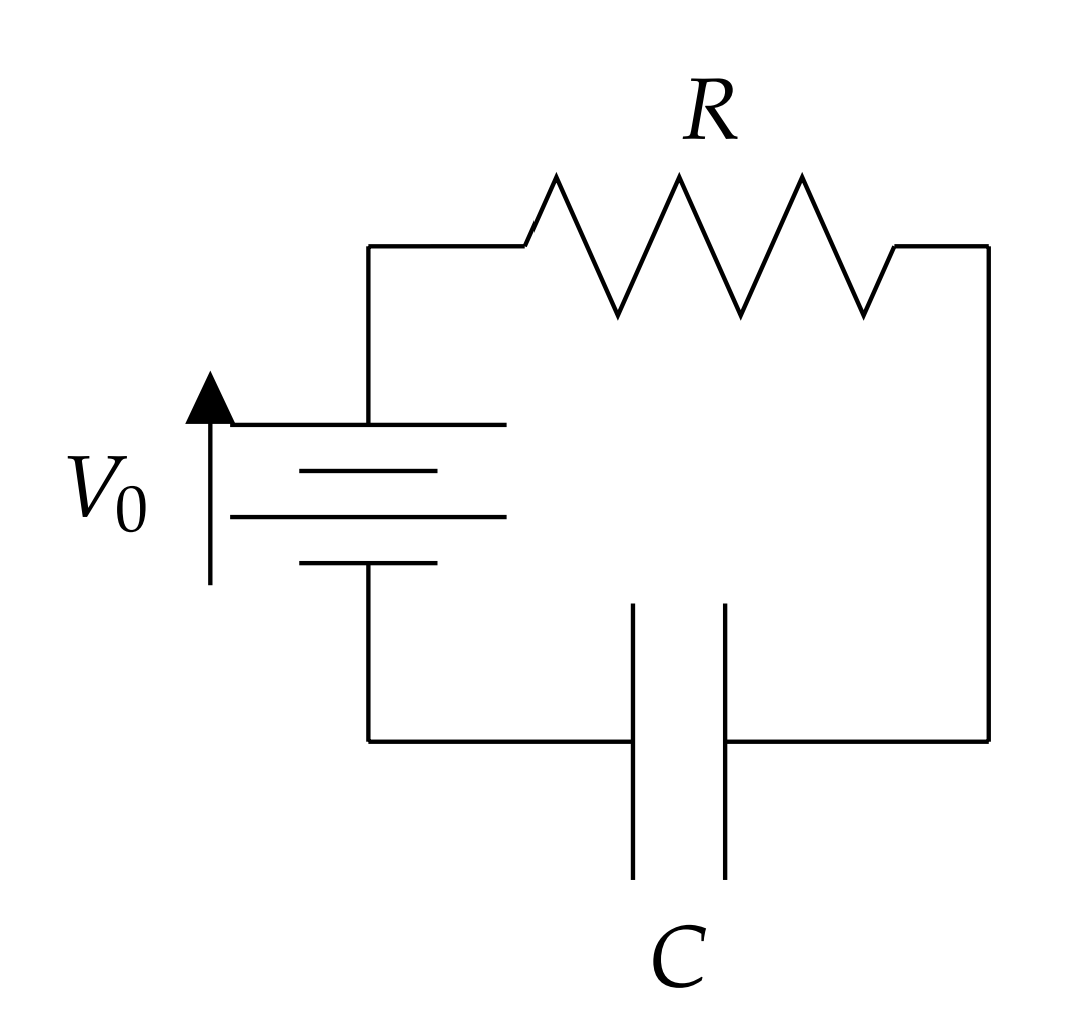
2.3.4: Circuitos RC
PRIMERO CONSIDERAMOS EL CASO DE UN CIRCUITO RC EN EL QUE NO HAY IN Además, consideraremos qué sucede cuando se carga un condensador con una batería de CC\(\left(V(t)=V_{0}\right)\) y cuando se descarga un condensador cargado\((V(t)=0)\) como se muestra en las Figuras\(\PageIndex{6}\) y\(\PageIndex{9}\).
Cargar un condensador.
Para cargar un condensador, tenemos el problema de valor inicial
\[R \dfrac{d q}{d t}+\dfrac{q}{C}=V_{0}, \quad q(0)=0 \nonumber \]
Esta ecuación es un ejemplo de una ecuación lineal de primer orden para\(q(t) .\) Sin embargo, también podemos reescribirla y resolverla como una ecuación separable, ya que\(V_{0}\) es una constante. Haremos lo primero sólo como otro ejemplo de encontrar el factor integrador.
Primero escribimos la ecuación en forma estándar:
\[\dfrac{d q}{d t}+\dfrac{q}{R C}=\dfrac{V_{0}}{R} \nonumber \]
El factor integrador es entonces
\(\mu(t)=e^{\int \dfrac{d t}{R C}}=e^{t / R C}\)
Por lo tanto,
\[\dfrac{d}{d t}\left(q e^{t / R C}\right)=\dfrac{V_{0}}{R} e^{t / R C} \nonumber \]
Integrando, tenemos
\[q e^{t / R C}=\dfrac{V_{0}}{R} \int e^{t / R C} d t=C V_{0} e^{t / R C}+K \nonumber \]
Tenga en cuenta que introdujimos la constante de integración,\(K\). Ahora divide lo exponencial para obtener la solución general:
\[q=C V_{0}+K e^{-t / R C} \nonumber \]
(Si hubiéramos olvidado el\(K\), no habríamos conseguido una solución correcta para la ecuación diferencial.)
A continuación, utilizamos la condición inicial para obtener la solución particular. A saber, el ajuste\(t=0\), tenemos que
\(0=q(0)=C V_{0}+K\)
Entonces,\(K=-C V_{0}\). Insertando esto en la solución, tenemos
\[q(t)=C V_{0}\left(1-e^{-t / R C}\right) \nonumber \]
Ahora podemos estudiar el comportamiento de esta solución. Para grandes tiempos el segundo término va a cero. Así, el condensador se carga, asintóticamente, al valor final de\(q_{0}=C V_{0} .\) Esto es lo que esperamos, porque la corriente ya no fluye\(R\) y esto solo da la relación entre la diferencia de potencial a través de las placas del condensador cuando una carga de \(q_{0}\)se establece en las placas.
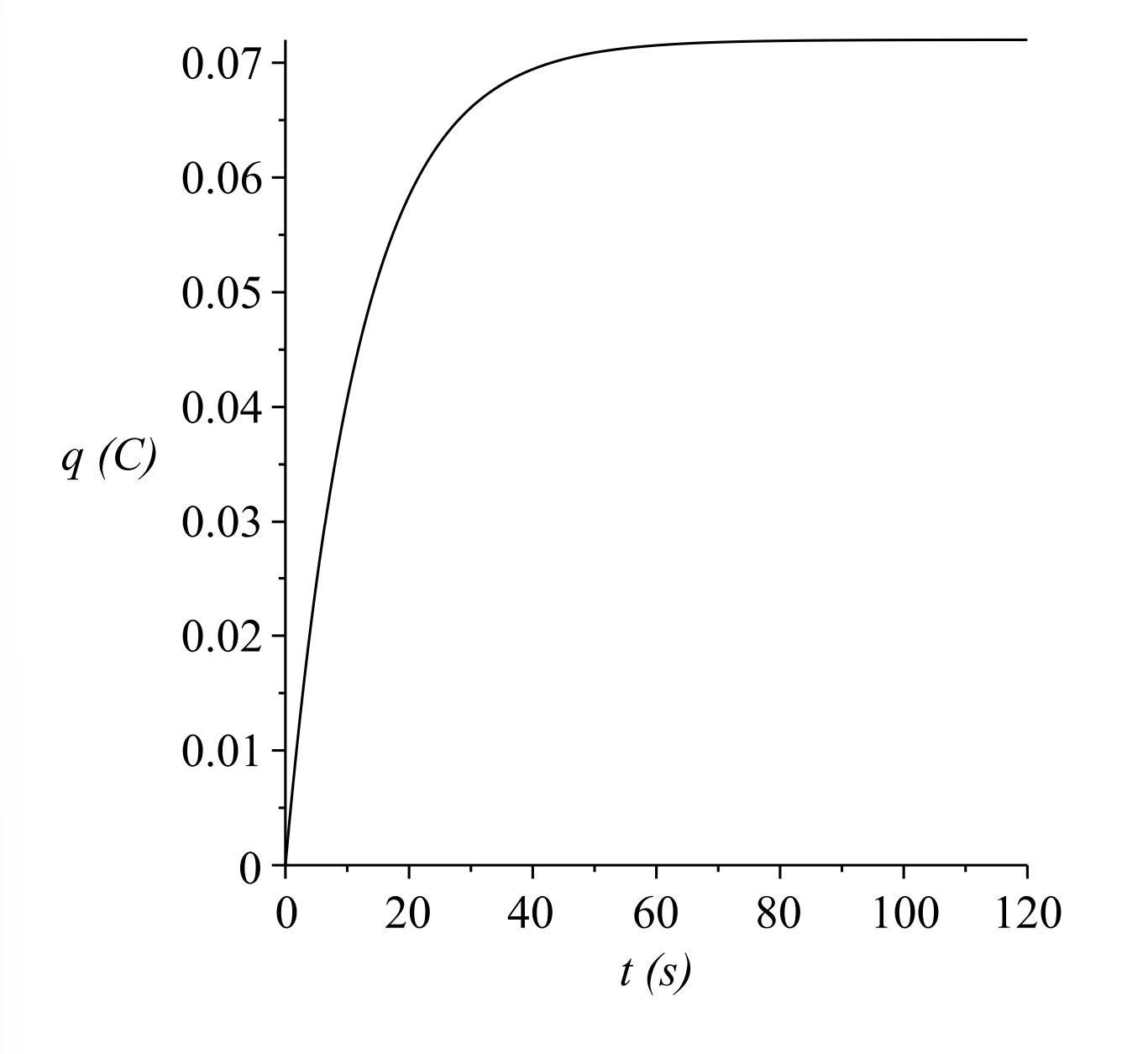
Pongamos algunos valores para los parámetros. Dejamos\(R = 2.00 k \omega \),\(C = 6.00\mathrm{mF}\), y\(V_{0}=12 \mathrm{~V} .\) Una gráfica de la solución se da en la Figura\(\PageIndex{7}\). Vemos que
la carga se acumula hasta el valor de\(C V_{0}=0.072 \mathrm{C}\). Si utilizamos una
resistencia menor,\(R=200 \Omega\), vemos en Figura\(\PageIndex{8}\) que el condensador se carga al
mismo valor, pero mucho más rápido.
Constante de tiempo,\(\tau=R C\).
La velocidad a la que un condensador carga, o descarga, se rige por la constante de tiempo,\(\tau=R C\). Este es el factor constante en lo exponencial. Cuanto más grande es, más lento decae el término exponencial. Si nos fijamos\(t = \tau\), nos encontramos con que
\(q(\tau)=C V_{0}\left(1-e^{-1}\right)=(1-0.3678794412 \ldots) q_{0} \approx 0.63 q_{0}\)
Así, en el momento\(t=\tau\), el condensador casi se ha cargado a dos tercios de su valor final. Para el primer conjunto de parámetros,\(\tau=12 \mathrm{~s}\). Para el segundo set,\(\tau=1.2 \mathrm{~s}\).
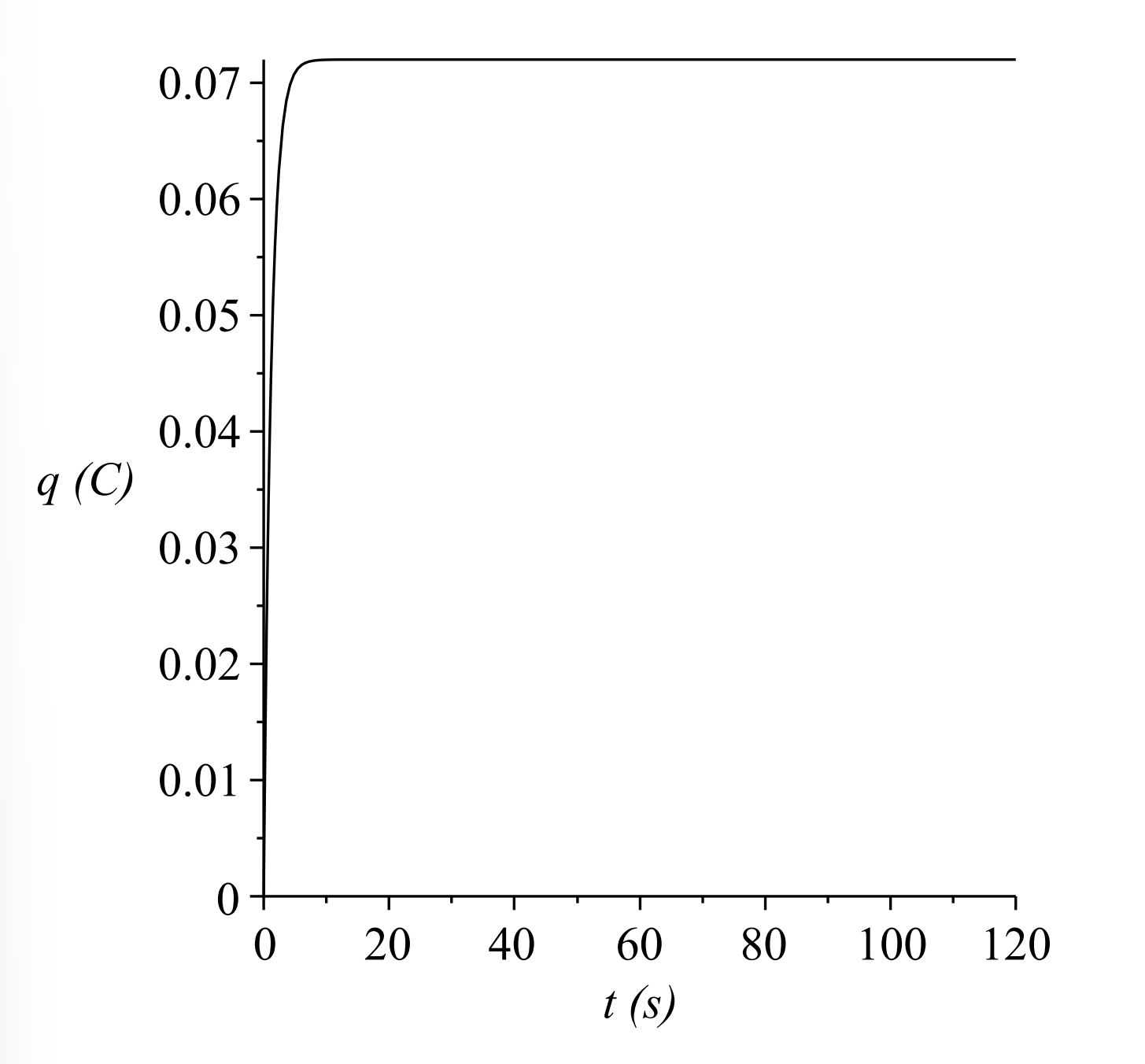Figura\(\PageIndex{8}\): The charge as a function of time for a charging capacitor with \(R=200 \Omega\), \(C=6.00 \mathrm{mF}\), y\(V_{0}=12 \mathrm{~V}\)Descargando un condensador.
Ahora, supongamos que el condensador está cargado de carga\(\pm q_{0}\) en sus placas. Si desconectamos la batería y volvemos a conectar los cables para completar el circuito como se muestra en la Figura\(\PageIndex{9}\), la carga luego se moverá fuera de las placas, descargando el condensador. La forma relevante del problema de valor inicial se convierte
\[R \dfrac{d q}{d t}+\dfrac{q}{C}=0, \quad q(0)=q_{0} . \nonumber \]
Esta ecuación es más sencilla de resolver. Reordenando, tenemos
\[\dfrac{d q}{d t}=-\dfrac{q}{R C} \nonumber \]
Este es un problema simple de decaimiento exponencial, que se puede resolver usando la separación de variables. No obstante, a estas alturas ya deberías saber cómo anotar de inmediato la solución a tales problemas de la forma\(y^{\prime}=k y\). La solución es
\(q(t)=q_{0} e^{-t / \tau}, \quad \tau=R C\)
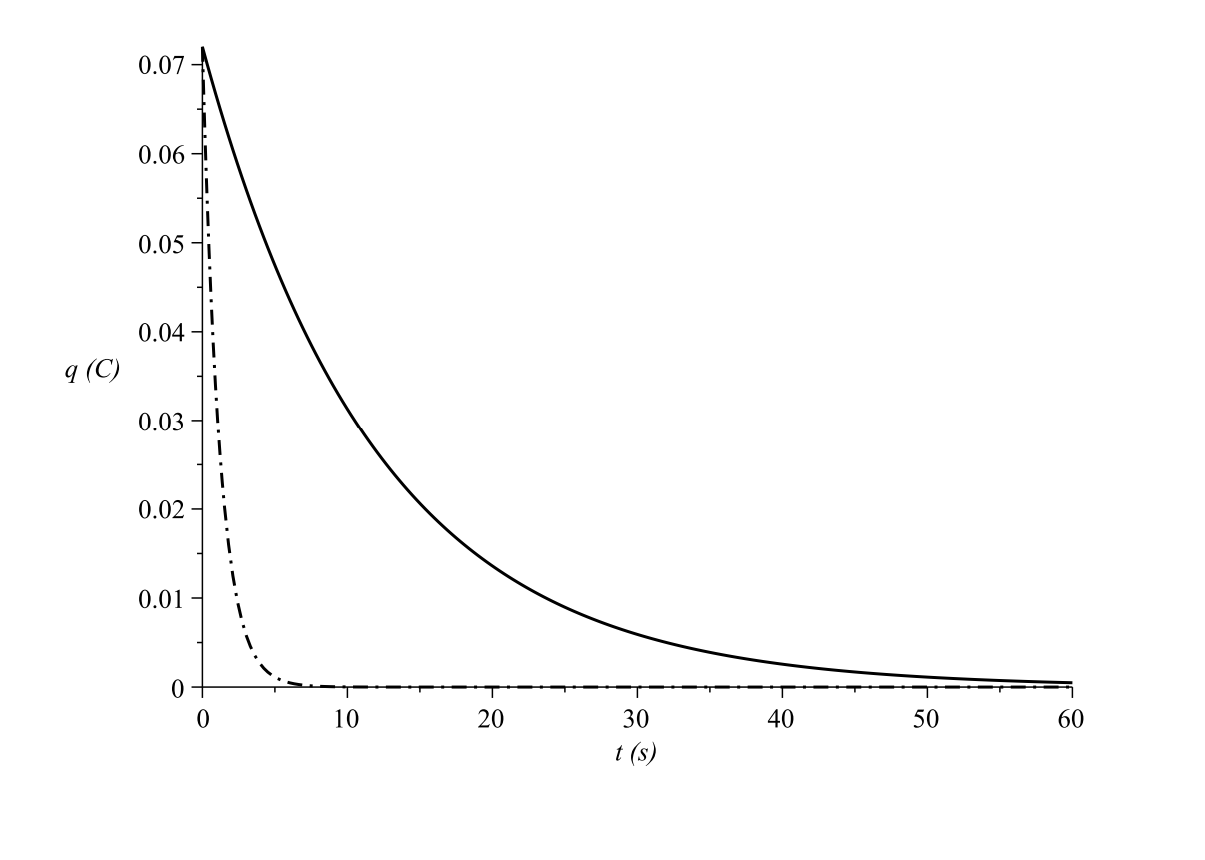
Vemos que la carga decae exponencialmente. En principio, el condensador nunca se descarga completamente. Es por eso que a menudo se le indica que coloque una derivación a través de un condensador descargado para descargarla por completo. En Figura\(\PageIndex{10} we show the discharging of the two previous RC circuits. Once again, \(\tau=R C\) determina el comportamiento. En\(t=\tau\) tenemos
\(q(\tau)=q_{0} e^{-1}=(0.3678794412 \ldots) q_{0} \approx 0.37 q_{0}\)
Entonces, en este momento el condensador sólo tiene alrededor de un tercio de su valor original.
2.3.5: Circuitos LC
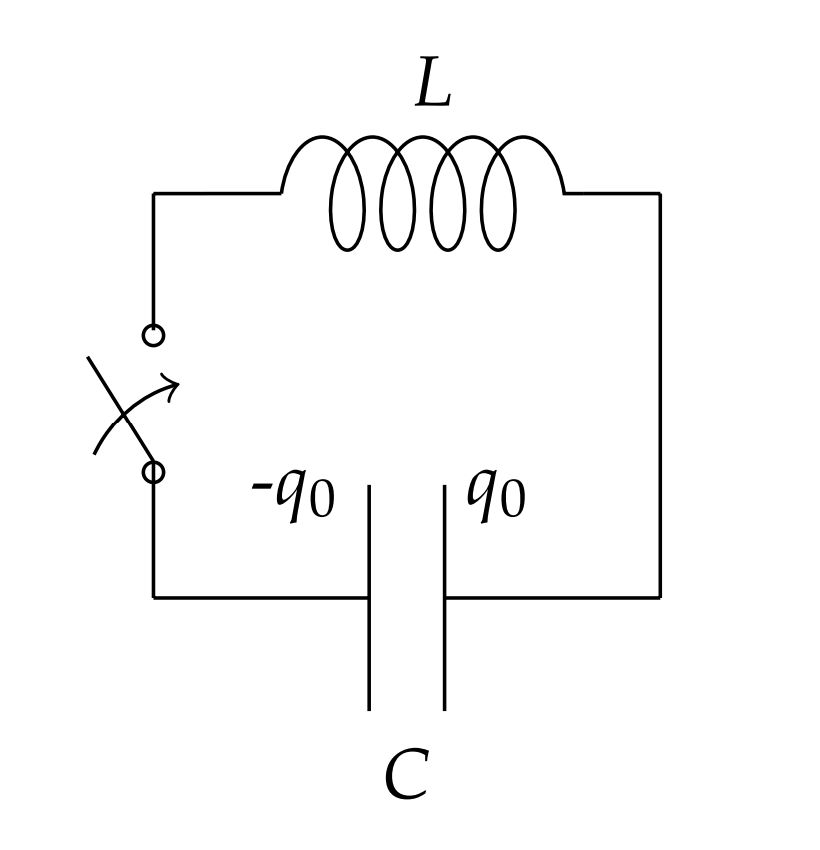
Osciladores LC.
OTRO RESULTADO SIMPLE proviene de estudiar\(L C\) circuitos. Ahora conectaremos un condensador cargado a un inductor como se muestra en la Figura\(\PageIndex{11}\). En este caso, consideramos el problema de valor inicial
\[L \ddot{q}+\dfrac{1}{C} q=0, \quad q(0)=q_{0}, \dot{q}(0)=I(0)=0 \nonumber \]
Dividiendo la inductancia, tenemos
\[\ddot{q}+\dfrac{1}{L C} q=0 \nonumber \]
Esta ecuación es una ecuación de coeficiente constante de segundo orden. Es de la misma forma que los de simple movimiento armónico de una masa sobre un resorte o el péndulo lineal. Entonces, esperamos un comportamiento oscilatorio. La ecuación característica es
\(r^{2}+\dfrac{1}{L C}=0\)
Las soluciones son
\(r_{1,2}=\pm \dfrac{i}{\sqrt{L C}}\)
Así, la solución de la Ecuación\(\PageIndex{15}\) es de la forma
\[ q(t)=c_{1} \cos (\omega t)+c_{2} \sin (\omega t), \quad \omega=(L C)^{-1 / 2} \nonumber \]
Inserción de los rendimientos de las condiciones iniciales
\[q(t)=q_{0} \cos (\omega t) \nonumber \]
Las oscilaciones que resultan son comprensibles. A medida que la carga sale de las placas, la corriente cambiante induce un campo magnético cambiante en el inductor. La energía eléctrica almacenada en el condensador cambia a energía magnética almacenada en el inductor. Sin embargo, el proceso continúa hasta que las placas se cargan con polaridad opuesta y luego el proceso comienza a la inversa. El condensador cargado luego se descarga y el condensador eventualmente vuelve a su estado original y todo el sistema repite esto una y otra vez.
La frecuencia de este simple movimiento armónico se encuentra fácilmente. Está dado por
\[f=\dfrac{\omega}{2 \pi}=\dfrac{1}{2 \pi} \dfrac{1}{\sqrt{L C}} \nonumber \]
A esto se le llama frecuencia de sintonización debido a su papel en los circuitos de sintonización.
Encuentra la frecuencia resonante para\(C=10 \mu \mathrm{F}\) y\(L=\)\(100 \mathrm{mH}\).
\(f=\dfrac{1}{2 \pi} \dfrac{1}{\sqrt{\left(10 \times 10^{-6}\right)\left(100 \times 10^{-3}\right)}}=160 \mathrm{~Hz}\)
Por supuesto, esta es una situación ideal. Siempre hay resistencia en el circuito, aunque solo sea una pequeña cantidad de los cables. Entonces, realmente necesitamos dar cuenta de la resistencia, o incluso agregar una resistencia. Esto lleva a un sistema un poco más complicado en el que estará presente la amortiguación.
2.3.6: Oscilaciones amortiguadas
COMO HEMOS INDICADO, el movimiento armónico simple es una situación ideal. En los sistemas reales a menudo tenemos que hacer frente a alguna pérdida de energía en el sistema. Esto conduce a la amortiguación de las oscilaciones. Un ejemplo estándar es un sistema resorte-masa-amortiguador como se muestra en la Figura, la\(2.12 \mathrm{~A}\) masa se une a un resorte y se agrega un amortiguador que puede absorber parte de la energía de las oscilaciones. la amortiguación se modela con un término proporcional a la velocidad.
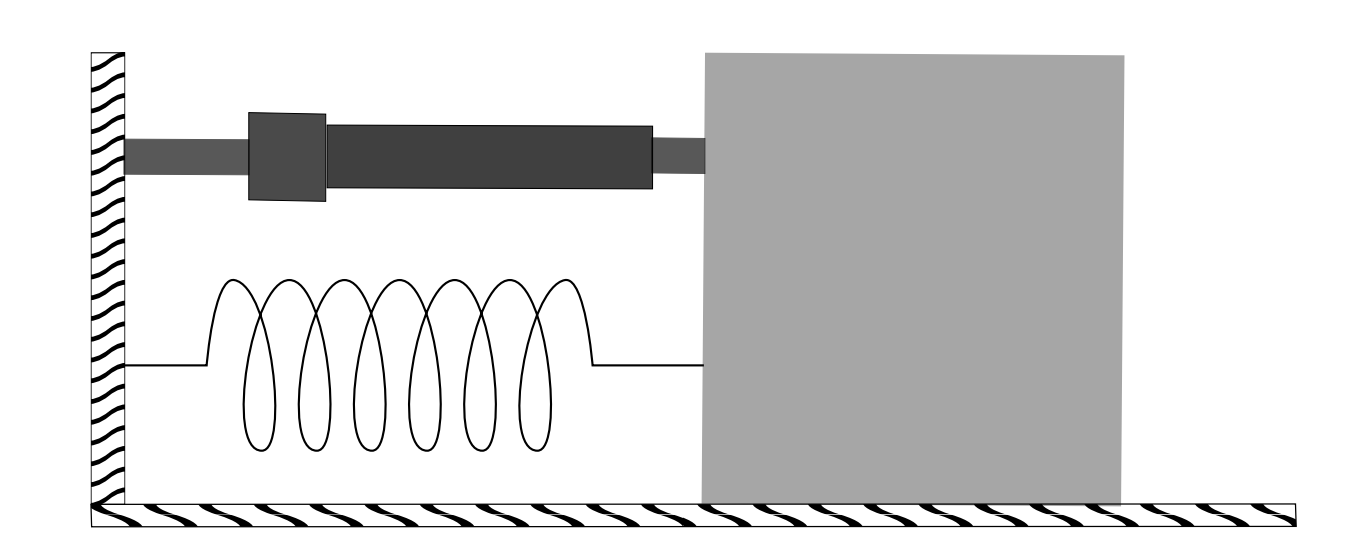
Existen otros modelos para oscilaciones en los que la pérdida de energía podría ser en el resorte, en la forma en que se une un péndulo a su soporte, o en la resistencia al flujo de corriente en un circuito LC. Los modelos más simples de resistencia son la adición de un término proporcional a la primera derivada de la variable dependiente. Por lo tanto, nuestros tres ejemplos principales con amortiguación agregada se ven así:
\[m \ddot{x}+b \dot{x}+k x=0 . \nonumber \]
\[L \ddot{\theta}+b \dot{\theta}+g \theta=0 . \nonumber \]
\[L \ddot{q}+R \dot{q}+\dfrac{1}{C} q=0 . \nonumber \]
Todos estos son ejemplos de la ecuación de coeficiente constante general
\[a y^{\prime \prime}(x)+b y^{\prime}(x)+c y(x)=0 \nonumber \]
Hemos visto que las soluciones se obtienen al observar la ecuación característica\(ar^2 + br + c = 0\). Esto lleva a tres comportamientos diferentes dependiendo del discriminante en la fórmula cuadrática:
\[r=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber \]
Consideraremos el ejemplo del muelle amortiguado. Entonces tenemos
\[r=\dfrac{-b \pm \sqrt{b^{2}-4 m k}}{2 m} \nonumber \]
Cajas de oscilador amortiguadas: sobreamortiguadas, amortiguadas críticamente y amortiguadas.
Sobrehumedecido,\(b^{2}>4 m k\)
En este caso obtenemos dos raíces reales. Dado que este es el Caso I para ecuaciones de coeficiente constante, tenemos que
\(x(t)=c_{1} e^{r_{1} t}+c_{2} e^{r_{2} t}\)
Tomamos nota de eso\(b^{2}-4 m k<b^{2}\). Así, las raíces son ambas negativas. Entonces, ambos términos en la solución decaen exponencialmente. El amortiguamiento es tan fuerte que no hay oscilación en el sistema.
Amortiguado críticamente,\(b^{2}=4 m k\)
En este caso obtenemos una raíz real. Este es el Caso II para ecuaciones de coeficiente constante y la solución viene dada por
\(x(t)=\left(c_{1}+c_{2} t\right) e^{r t}\)
donde\(r=-b / 2 m .\) Una vez más, la solución decae exponencialmente. La amortiguación es lo suficientemente fuerte como para dificultar cualquier oscilación. Si fuera más débil el discriminante sería negativo y necesitaríamos el tercer caso.
Subamortiguado,\(b^{2}<4 m k\)
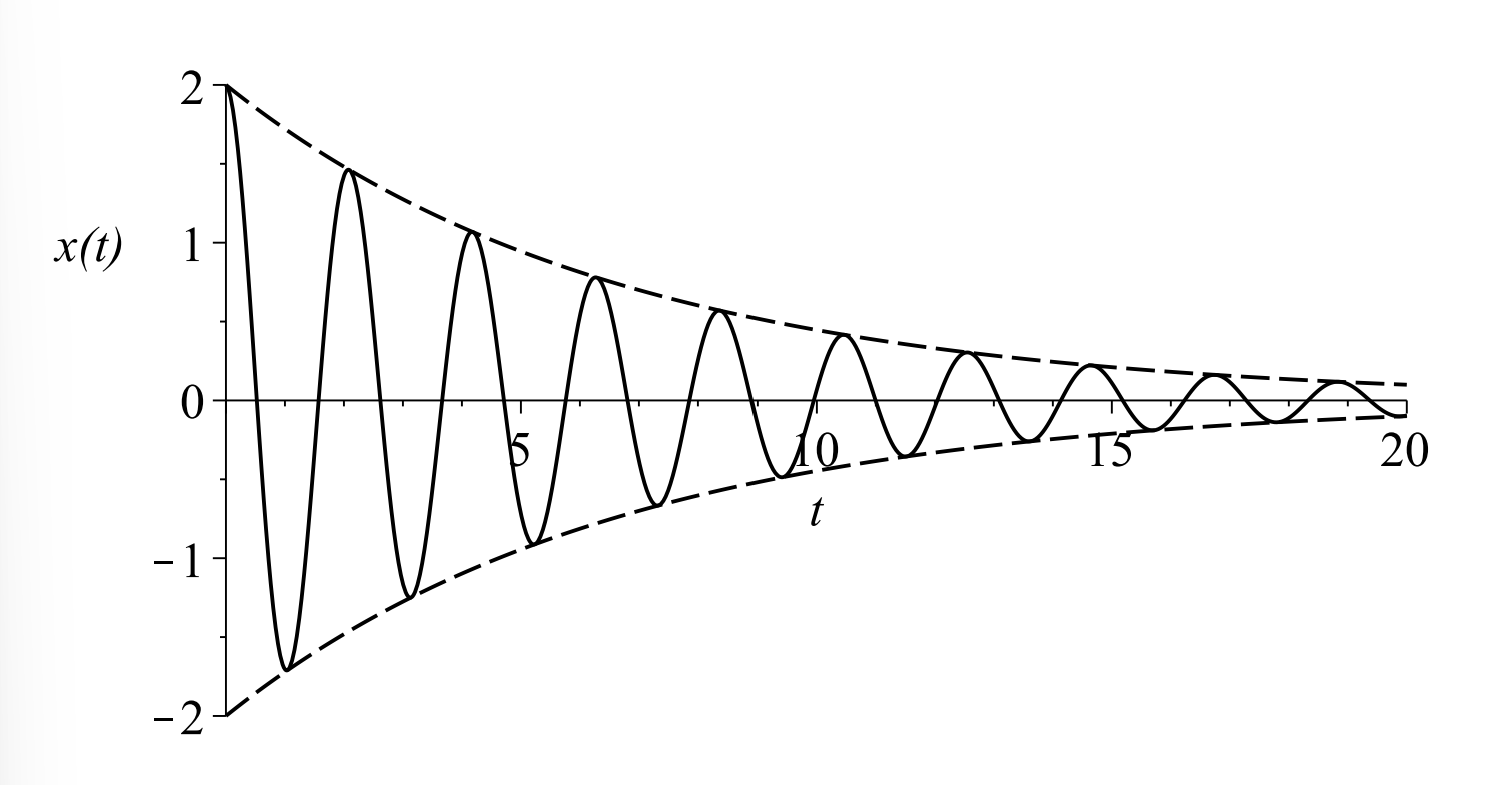
En este caso tenemos raíces conjugadas complejas. Podemos escribir\(\alpha=-b / 2 m\) y\(\beta=\sqrt{4 m k-b^{2}} / 2 m .\) Entonces la solución es
\(x(t)=e^{\alpha t}\left(c_{1} \cos \beta t+c_{2} \sin \beta t\right)\)
Estas soluciones exhiben oscilaciones debidas a las funciones trigonométricas, pero vemos que la amplitud puede decairse en el tiempo debido al factor general de\(e^{\alpha t}\) cuando\(\alpha<0 .\) Consideremos el caso que las condiciones iniciales dan\(c_{1}=A\) y\(c_{2}=0 .\) (Cuando es esto?) Entonces, la solución,\(x(t)=A e^{\alpha t} \cos \beta t\), se parece a la trama de la Figura\(\PageIndex{13}.\)