2.4: Sistemas Forzados
- Page ID
- 119686
TODOS LOS SISTEMAS PRESENTADOS al inicio de la última sección presentan el mismo comportamiento general cuando se presenta un término de amortiguación. Se puede agregar un término adicional que podría causar un comportamiento aún más complicado. En el caso de los circuitos LRC, hemos visto que la fuente de voltaje hace que el sistema no sea homogéneo. Proporciona lo que se llama término fuente. Tales términos también pueden surgir en los sistemas masa-resorte y péndulo. Uno puede impulsar dichos sistemas empujando periódicamente la masa, o haciendo que todo el sistema se mueva, o impactado por una fuerza externa. Tales sistemas se llaman forzados, o impulsados.
Los sistemas típicos en física pueden modelarse mediante ecuaciones de segundo orden no homogéneas. Así, queremos encontrar soluciones de ecuaciones de la forma
\[L y(x)=a(x) y^{\prime \prime}(x)+b(x) y^{\prime}(x)+c(x) y(x)=f(x) \label{2.43} \]
Como se señala en la Sección 2.1, se resuelve esta ecuación encontrando la solución general del problema homogéneo,
\(L y_{h}=0\)
y una solución particular del problema no homogéneo,
\(L y_{p}=f .\)
Entonces, la solución general de Ecuación simplemente\(2.1.1\) se da como\(y=y_{h}+y_{p}\).
Hasta el momento, sólo sabemos resolver coeficientes constantes, ecuaciones homogéneas. Entonces, al agregar un término no homogéneo a tales ecuaciones necesitaremos encontrar la solución particular a la ecuación no homogénea.
Podríamos adivinar una solución, pero eso no suele ser posible sin un poco de experiencia. Entonces, necesitamos algunos otros métodos. Hay dos métodos principales. En el primer caso, el Método de Coeficientes Indeterminados, se hace una suposición inteligente basada en la forma de\(f(x)\). En el segundo método, se puede desarrollar sistemáticamente la solución particular. Volveremos al Método de Variación de Parámetros y además presentaremos la poderosa maquinaria de las funciones de Green más adelante en esta sección.
Método de Coeficientes Indeterminados
RESOLVEMOS UNA ECUACIÓN DIFERENCIAL SIMPLE destacando cómo podemos manejar ecuaciones no homogéneas.
Considera la ecuación
\[y^{\prime \prime}+2 y^{\prime}-3 y=4 \nonumber \]
El primer paso es determinar la solución de la ecuación homogénea. Así, resolvemos
\[y_{h}^{\prime \prime}+2 y_{h}^{\prime}-3 y_{h}=0 \nonumber \]
La ecuación característica es\(r^{2}+2 r-3=0 .\) Las raíces son\(r=1,-3\). Entonces, podemos escribir de inmediato la solución
\(y_{h}(x)=c_{1} e^{x}+c_{2} e^{-3 x}\)
El segundo paso es encontrar una solución particular de Ecuación\(\PageIndex{2}\). ¿Qué función posible podemos insertar en esta ecuación de tal manera que solo quede un 4? Si intentamos algo proporcional a\(x\), entonces nos quedamos con una función lineal después de insertar\(x\) y sus derivadas. Quizás una función constante se podría pensar. \(y=4\)no funciona. Pero, podríamos intentar una constante arbitraria,\(y=A\).
A ver. Insertando\(y=A\) en la ecuación\(\PageIndex{2}\), obtenemos
\(-3 A=4\)
¡Ah, ja! Vemos que podemos elegir\(A=-\dfrac{4}{3}\) y esto funciona. Entonces, tenemos una solución particular,\(y_{p}(x)=-\dfrac{4}{3}\). Este paso está hecho.
Combinando las dos soluciones, tenemos la solución general a la ecuación original no homogénea Ecuación\(\PageIndex{2}\). A saber,
\(y(x)=y_{h}(x)+y_{p}(x)=c_{1} e^{x}+c_{2} e^{-3 x}-\dfrac{4}{3}\)
Inserte esta solución en la ecuación y verifique que efectivamente sea una solución. Si se nos hubieran dado condiciones iniciales, ahora podríamos utilizarlas para determinar las constantes arbitrarias.
¿Y si tuviéramos un término fuente diferente? Considera la ecuación
\[y^{\prime \prime}+2 y^{\prime}-3 y=4 x \nonumber \]
Lo único que cambiaría es la solución particular. Entonces, necesitamos una conjetura.
Sabemos que una función constante no funciona por el último ejemplo. Entonces, intentemos\(y_{p}=A x\). Insertando esta función en la ecuación\(\PageIndex{4}\), obtenemos
\(2 A-3 A x=4 x\)
Picking\(A=-4 / 3\) se desharía de los\(x\) términos, pero no lo cancelará todo. Todavía tenemos una izquierda constante. Entonces, necesitamos algo más general.
Probemos una función lineal,\(y_{p}(x)=A x+B\). Luego obtenemos después de la sustitución en Ecuación\(\PageIndex{4}\)
\[2 A-3(A x+B)=4 x \nonumber \]
Igualando los coeficientes de las diferentes potencias de ambos\(x\) lados, encontramos un sistema de ecuaciones para los coeficientes indeterminados:
\[ \begin{array}{r} 2 A-3 B=0 \\ -3 A=4 \end{array}\label{2.47} \]
Estos se resuelven fácilmente para obtener
\[ \begin{aligned} A &=-\dfrac{4}{3} \\ B &=\dfrac{2}{3} A=-\dfrac{8}{9} \end{aligned}\label{48} \]
Entonces, la solución particular es
\(y_{p}(x)=-\dfrac{4}{3} x-\dfrac{8}{9}\)
Esto da la solución general al problema no homogéneo como
\(y(x)=y_{h}(x)+y_{p}(x)=c_{1} e^{x}+c_{2} e^{-3 x}-\dfrac{4}{3} x-\dfrac{8}{9}\)
Hay formas generales que puedes adivinar con base en la forma del término de conducción,\(f(x)\). Algunos ejemplos se dan en la Tabla\(\PageIndex{1}\). Aplicaciones más generales están cubiertas en un texto estándar sobre ecuaciones diferenciales. No obstante, el procedimiento es sencillo. Dado\(f(x)\) en una forma particular, haces una conjetura apropiada hasta algunos parámetros desconocidos, o coeficientes. Insertar la conjetura conduce a un sistema de ecuaciones para los coeficientes desconocidos. Resuelve el sistema y tienes la solución. Esta solución se agrega luego a la solución general de la ecuación diferencial homogénea.
| \(f(x)\) | Adivina |
|
\(a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}\) \(a e^{b x}\) \(a \cos \omega x+b \sin \omega x\) |
\(A_{n} x^{n}+A_{n-1} x^{n-1}+\cdots+A_{1} x+A_{0}\) \(A e^{b x}\) \(A \cos \omega x+B \sin \omega x\) |
Resolver
\[y^{\prime \prime}+2 y^{\prime}-3 y=2 e^{-3 x} \nonumber \]
De acuerdo con lo anterior, adivinaríamos una solución de la forma\(y_{p}=A e^{-3 x} .\) Insertando nuestra conjetura, encontramos
\(0=2 e^{-3 x}\)
¡Uy! ¡El coeficiente,\(A\), desapareció! No podemos resolverlo. ¿Qué salió mal?
La respuesta está en la solución general del problema homogéneo. Tenga en cuenta que\(e^{x}\) y\(e^{-3 x}\) son soluciones al problema homogéneo. Entonces, un múltiplo de no nos\(e^{-3 x}\) llevará a ningún lado. Resulta que hay una modificación más del método. Si el término de conducción contiene términos que son soluciones del problema homogéneo, entonces necesitamos hacer una conjetura consistente en la menor potencia posible de\(x\) veces la función que ya no es una solución del problema homogéneo. A saber, adivinamos\(y_{p}(x)=A x e^{-3 x}\) y diferenciamos esta suposición para obtener los derivados\(y_{p}^{\prime}=A(1-3 x) e^{-3 x}\) y\(y_{p}^{\prime \prime}=A(9 x-6) e^{-3 x}\)
Insertando estas derivadas en la ecuación diferencial, obtenemos
\([(9 x-6)+2(1-3 x)-3 x] A e^{-3 x}=2 e^{-3 x}\)
Comparando coeficientes, tenemos
\(-4 A=2\)
Entonces,\(A=-1 / 2\) y\(y_{p}(x)=-\dfrac{1}{2} x e^{-3 x}\). Así, la solución al problema es
\(y(x)=\left(2-\dfrac{1}{2} x\right) e^{-3 x}\)
Método Modificado de Coeficientes Indeterminados
En general, si algún término en la conjetura\(y_{p}(x)\) es una solución de la ecuación homogénea, entonces multiplique la conjetura por\(x^{k}\), donde\(k\) está el entero positivo más pequeño tal que ningún término in\(x^{k} y_{p}(x)\) es una solución del problema homogéneo.
2.4.2: Oscilaciones forzadas periódicamente
UN TIPO ESPECIAL DE FORZAMIENTO es el forzamiento periódico. Las oscilaciones realistas se amortiguarán y eventualmente se detendrán si se dejan desatendidas. Por ejemplo, los relojes mecánicos son accionados por péndula compuesta o torsional y los osciladores eléctricos a menudo se diseñan con la necesidad de continuar por largos períodos de tiempo. Sin embargo, no son máquinas de movimiento perpetuo y necesitarán una inyección periódica de energía. Esto se puede hacer sistemáticamente agregando forzamientos periódicos. Otro ejemplo sencillo es el movimiento de un niño en un columpio en el parque. Este simple sistema de péndulo amortiguado naturalmente disminuirá al equilibrio (detenido) si se deja solo. Sin embargo, si el niño bombea energía al columpio en el momento adecuado, o si un adulto empuja al niño en el momento adecuado, entonces se puede aumentar la amplitud del columpio.
Existen otros sistemas, como alas de avión y largos tramos de puente, en los que fuerzas impulsoras externas podrían causar daños al sistema. Un ejemplo bien conocido es el colapso inducido por el viento del Puente Tacoma Narrows debido a fuertes vientos. Por supuesto, si uno no tiene cuidado, el niño en el último ejemplo podría recibir demasiada energía bombeada al sistema provocando una falla similar del movimiento deseado.
El Puente Tacoma Narrows abrió en el estado de Washington (Estados Unidos) a mediados\(1940 .\) Sin embargo, en noviembre del mismo año los vientos excitaron un modo transversal de vibración, que eventualmente (en pocas horas) conducen a oscilaciones de gran amplitud para luego colapsar.
Si bien hay muchos tipos de sistemas forzados, y algunos bastante complicados, podemos llegar fácilmente a las características básicas de las oscilaciones forzadas modificando el sistema masa-resorte agregando una fuerza impulsora externa, dependiente del tiempo. Tal como sistema satisface la ecuación
\[m \ddot{x}+\dot{b(x)}+k x=F(t) \nonumber \]
donde\(m\) esta la masa,\(b\) es la constante de amortiguacion,\(k\) es la constante de resorte, y\(F(t)\) es la fuerza impulsora. Si\(F(t)\) es de forma simple, entonces podemos emplear el Método de Coeficientes Indeterminados. Dado que los sistemas que hemos considerado hasta ahora son similares, se podría aplicar fácilmente lo siguiente a péndula o circuitos.
Como el término de amortiguación sólo complica la solución, consideraremos el caso más simple del movimiento sin amortiguar y asumirlo\(b=0\). Además, introduciremos una fuerza motriz sinusoidal, con\(F(t)=F_{0} \cos \omega t\) el fin de estudiar el forzamiento periódico. Esto conduce a la simple masa conducida periódicamente en un sistema de resorte
\[m \ddot{x}+k x=F_{0} \cos \omega t . \nonumber \]
Para encontrar la solución general, primero obtenemos la solución al problema homogéneo,
\(x_{h}=c_{1} \cos \omega_{0} t+c_{2} \sin \omega_{0} t\)
donde\(\omega_{0}=\sqrt{\dfrac{k}{m}} .\) A continuación, buscamos una solución particular al problema no homogéneo. Aplicaremos el Método de Coeficientes Indeterminados.
Una suposición natural para la solución particular sería usar\(x_{p}=A \cos \omega t+B \sin \omega t\). No obstante, recordemos que la conjetura no debe ser una solución del problema homogéneo. Comparando\(x_{p}\) con\(x_{h}\), esto se mantendría si de\(\omega \neq \omega_{0} .\) lo contrario, se necesitaría usar el Método Modificado de Coeficientes Indeterminados como se describe en la última sección. Entonces, tenemos dos casos a considerar.
Dividiendo por la masa, resolvemos el sistema impulsado simple,\(\ddot{x}+\omega_{0}^{2} x=\dfrac{F_{0}}{m} \cos \omega t\)
Resolver\(\ddot{x}+\omega_{0}^{2} x=\dfrac{F_{0}}{m} \cos \omega t\), para\(\omega \neq \omega_{0} .\)
En este caso seguimos con la conjetura\(x_{p}=A \cos \omega t+B \sin \omega t\).
Como no hay término de amortiguación, uno encuentra rápidamente que\(B=0 .\)\(x_{p}=A \cos \omega t\) Insertando en la ecuación diferencial, encontramos que
\(\left(-\omega^{2}+\omega_{0}^{2}\right) A \cos \omega t=\dfrac{F_{0}}{m} \cos \omega t\)
Resolviendo para A, obtenemos
\(A=\dfrac{F_{0}}{m\left(\omega_{0}^{2}-\omega^{2}\right)}\)
La solución general para este caso es,
\[x(t)=c_{1} \cos \omega_{0} t+c_{2} \sin \omega_{0} t+\dfrac{F_{0}}{m\left(\omega_{0}^{2}-\omega^{2}\right)} \cos \omega t \nonumber \]
Resolver\(\ddot{x}+\omega_{0}^{2} x=\dfrac{F_{0}}{m} \cos \omega_{0} t\).
En este caso, necesitamos emplear el Método Modificado de Coeficientes Indeterminados. Entonces, hacemos la conjetura\(x_{p}=A \cos \omega_0 t+B \sin \omega_0 t\). Como no hay término de amortiguación, se encuentra que A = 0. Insertando la suposición en la ecuación diferencial, encontramos que
\(B=\dfrac{F_{0}}{2 m \omega_{0}}\),
o la solución general es
\[x(t)=c_{1} \cos \omega_{0} t+c_{2} \sin \omega_{0} t+\dfrac{F_{0}}{2 m \omega} t \sin \omega t \nonumber \]
La solución general al problema es así
\[ x(t)=c_{1} \cos \omega_{0} t+c_{2} \sin \omega_{0} t+ \begin{cases}\dfrac{F_{0}}{m\left(\omega_{0}^{2}-\omega^{2}\right)} \cos \omega t, & \omega \neq \omega_{0} \\ \dfrac{F_{0}}{2 m \omega_{0}} t \sin \omega_{0} t, & \omega=\omega_{0}\end{cases} \label{2.54} \]
Los casos especiales de estas soluciones proporcionan una física interesante, que puede ser explorada por el lector en la tarea. En el caso de que\(\omega=\omega_{0}\), vemos que la solución tiende a crecer a medida que\(t\) se agranda. Esto es lo que se llama resonancia. Esencialmente, uno está impulsando el sistema a su frecuencia natural. A medida que el sistema se mueve hacia la izquierda, uno lo empuja hacia la izquierda. Si se está moviendo hacia la derecha, uno está agregando energía en esa dirección. Esto obliga a que la amplitud de oscilación continúe creciendo hasta que el sistema se rompa. Un ejemplo de tal oscilación se muestra en la Figura\(\PageIndex{2}\).
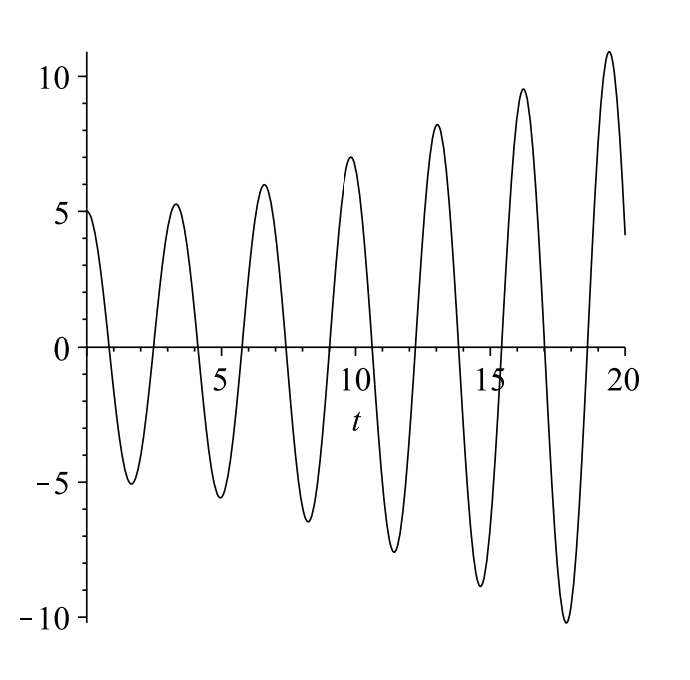Figura\(\PageIndex{2}\): Plot of \(x(t)=5 \cos 2 t+\dfrac{1}{2} t \sin 2 t\), a solution of \(\ddot{x}+4 x=2 \cos 2 t\) showing resonance. En el caso de que\(\omega \neq \omega_{0}\), se puede reescribir la solución de una forma sencilla. Escojamos las condiciones iniciales que\(c_{1}=-F_{0} /\left(m\left(\omega_{0}^{2}-\omega^{2}\right)\right), c_{2}=0 .\) Entonces uno tiene (ver Problema 13)
\[x(t)=\dfrac{2 F_{0}}{m\left(\omega_{0}^{2}-\omega^{2}\right)} \sin \dfrac{\left(\omega_{0}-\omega\right) t}{2} \sin \dfrac{\left(\omega_{0}+\omega\right) t}{2} \nonumber \]
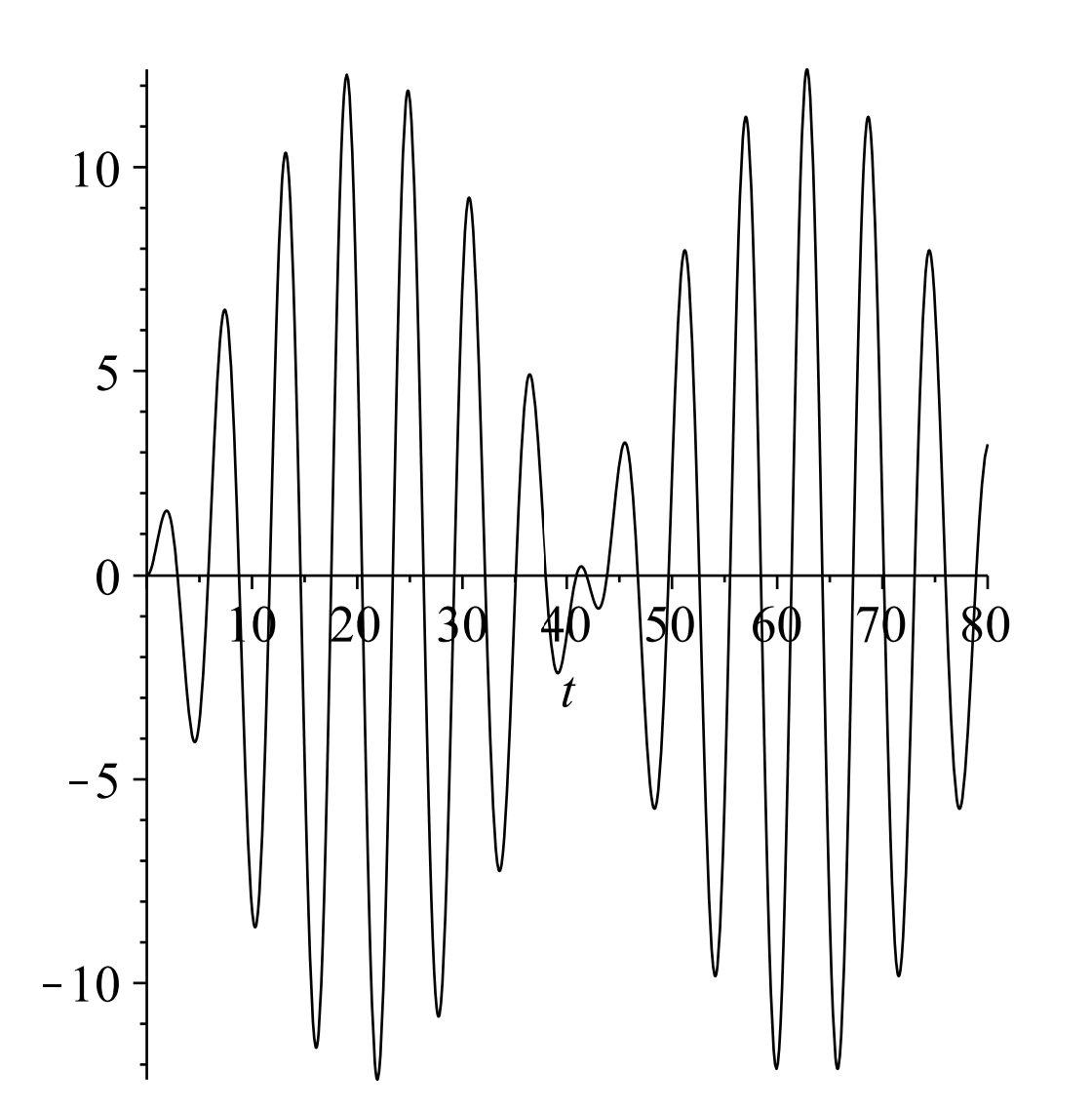
Para valores de\(\omega\) cerca\(\omega_{0}\), se encuentra que la solución consiste en una oscilación rápida, debido al\(\sin \dfrac{\left(\omega_{0}+\omega\right) t}{2}\) factor, con una amplitud que varía lentamente,\(\dfrac{2 F_{0}}{m\left(\omega_{0}^{2}-\omega^{2}\right)} \sin \dfrac{\left(\omega_{0}-\omega\right) t}{2} .\) El lector puede investigar esta solución.
Esta variación lenta se llama latido y la frecuencia de latido viene dada por\(f=\)\(\dfrac{\left|\omega_{0}-\omega\right|}{4 \pi} .\) En la Figura\(\PageIndex{3}\) vemos que las oscilaciones de alta frecuencia están contenidas por la frecuencia de latido inferior,\(f=\dfrac{0.15}{4 \pi} \mathrm{s}\). Esto corresponde a un periodo de\(T=1 / f \approx 83.7 \mathrm{~Hz}\), que se ve aproximadamente a la derecha de la figura.
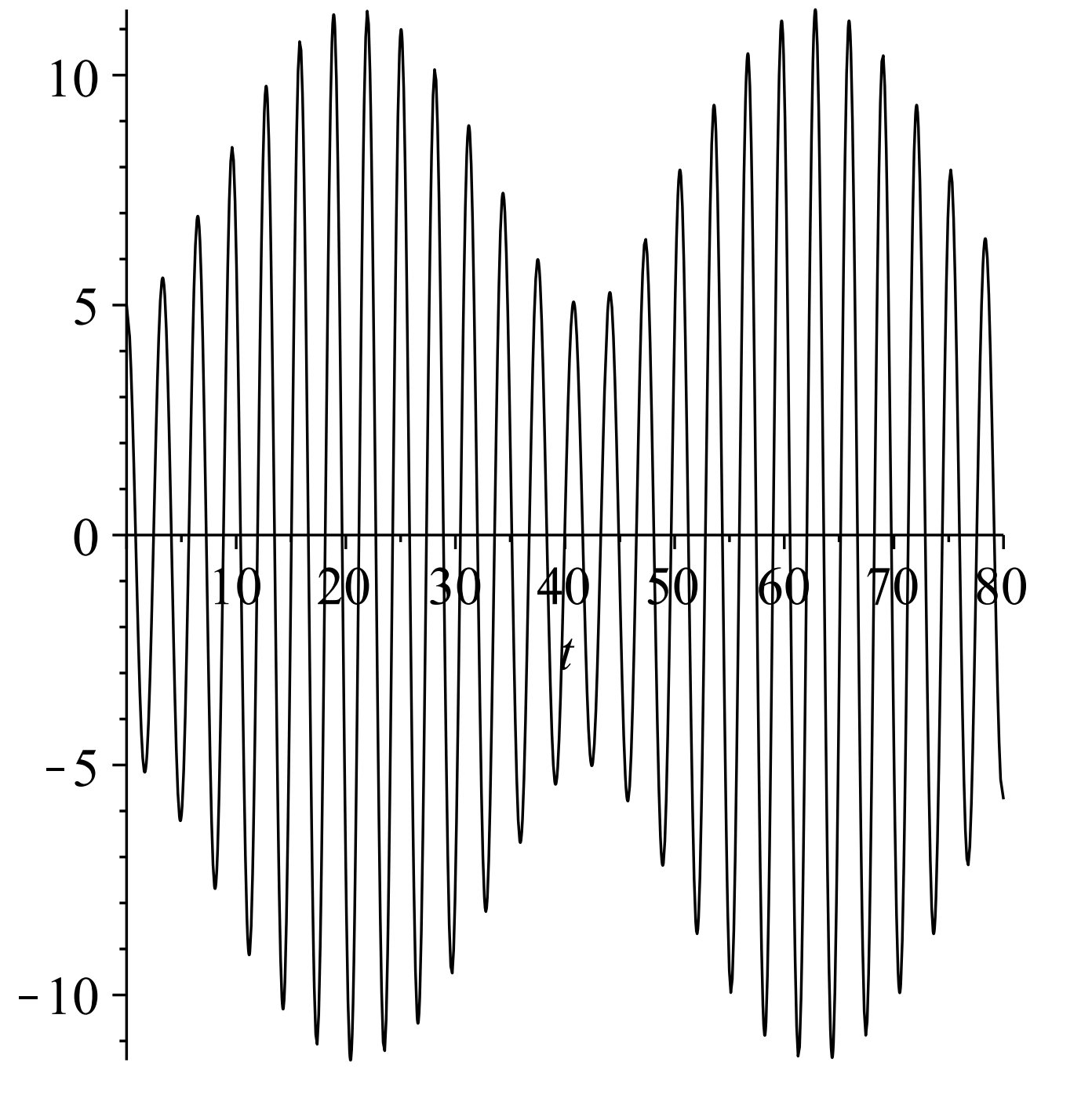
Resolver\(\ddot{x}+x=2 \cos \omega t, x(0)=0, \dot{x}(0)=0\),\(\omega=\)\(1,1.15 .\) para cada caso, necesitamos la solución del problema homogéneo,
\(x_{h}(t)=c_{1} \cos t+c_{2} \sin t .\)
La solución particular depende del valor de\(\omega\).
Porque\(\omega=1\), el término de conducción\(2 \cos \omega t\),, es una solución del problema homogéneo. Por lo tanto, asumimos
\(x_{p}(t)=A t \cos t+B t \sin t .\)
Insertando esto en la ecuación diferencial, encontramos\(A=0\) y\(B=1\). Entonces, la solución general es
\(x(t)=c_{1} \cos t+c_{2} \sin t+t \sin t\)
Imponiendo las condiciones iniciales, encontramos
\(x(t)=t \sin t\)
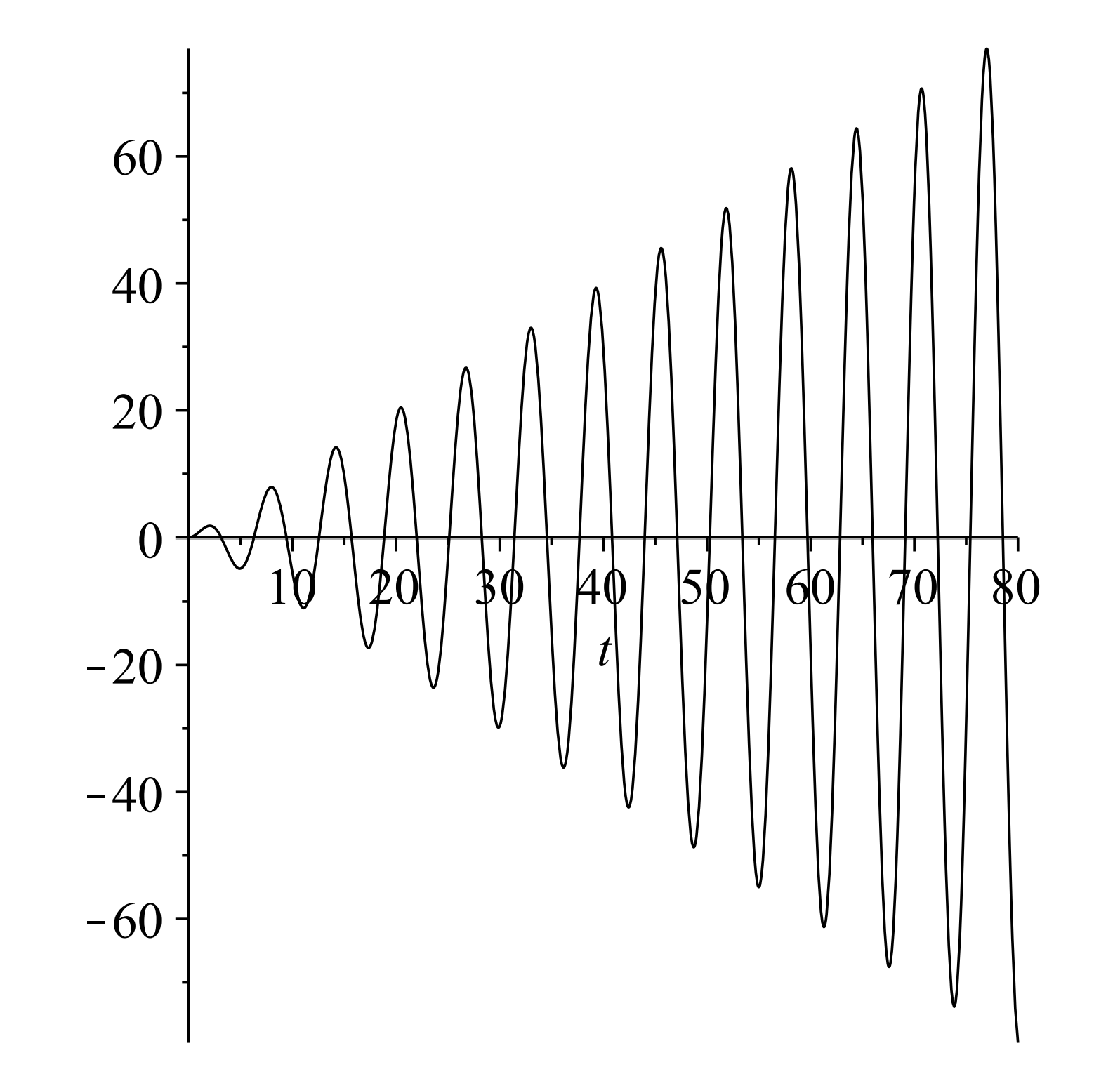
Esta solución se muestra en la Figura\(\PageIndex{4}\).
Porque\(\omega=1.15\), el término de conducción\(2 \cos \omega 1.15 t\),, no es una solución del problema homogéneo. Por lo tanto, asumimos
\(x_{p}(t)=A \cos 1.15 t+B \sin 1.15 t\)
Insertando esto en la ecuación diferencial, encontramos\(A=-\dfrac{800}{129}\) y\(B=0 .\) Entonces, la solución general es
\(x(t)=c_{1} \cos t+c_{2} \sin t-\dfrac{800}{129} \cos t\)
Imponiendo las condiciones iniciales, encontramos
\(x(t)=\dfrac{800}{129}(\cos t-\cos 1.15 t)\)
Esta solución se muestra en la Figura\(\PageIndex{5}\). La frecuencia de latido en este caso es la misma que con la Figura\(\PageIndex{3}\).
Reducción de orden para ecuaciones no homogéneas
El Método de Reducción del Orden también es útil para resolver problemas no homogéneos. En este caso si conocemos una solución del problema homogéneo, entonces podemos utilizarla para obtener una solución particular del problema no homogéneo. Por ejemplo, considere la ecuación diferencial no homogénea
\[a(x) y^{\prime \prime}(x)+b(x) y^{\prime}(x)+c(x) y(x)=f(x) \nonumber \]
Supongamos que\(y_{1}(x)\) satisface la ecuación diferencial homogénea
\[a(x) y_{1}^{\prime \prime}(x)+b(x) y_{1}^{\prime}(x)+c(x) y_{1}(x)=0 \nonumber \]
La, buscamos una solución particular,\(y_{p}(x)=v(x) y_{1}(x)\) sus derivados son dados por
\(\begin{aligned} y_{p}^{\prime} &=\left(v y_{1}\right)^{\prime} \\ &=v^{\prime} y_{1}+v y_{1}^{\prime} \\ y_{p}^{\prime \prime} &=\left(v^{\prime} y_{1}+v y_{1}^{\prime}\right)^{\prime} \\ &=v^{\prime \prime} y_{1}+2 v^{\prime} y_{1}^{\prime}+v y_{1}^{\prime \prime} \end{aligned} \)
Sustituyendo\(y_{p}\) y sus derivadas en la ecuación diferencial, tenemos
\(\begin{aligned} f &=a y_{p}^{\prime \prime}+b y_{p}^{\prime}+c y_{p} \\ &=a\left(v^{\prime \prime} y_{1}+2 v^{\prime} y_{1}^{\prime}+v y_{1}^{\prime \prime}\right)+b\left(v^{\prime} y_{1}+v y_{1}^{\prime}\right)+c v y_{1} \\ &=a v^{\prime \prime} y_{1}+2 a v^{\prime} y_{1}^{\prime}+b v^{\prime} y_{1}+v\left[a y_{1}^{\prime \prime}+b y_{1}^{\prime}+c y_{1}\right] \\ &=a v^{\prime \prime} y_{1}+2 a v^{\prime} y_{1}^{\prime}+b v^{\prime} y_{1} \end{aligned}\)
Por lo tanto,\(v(x)\) satisface la ecuación de segundo orden
\(a(x) y(x) v^{\prime \prime}(x)+\left[2 a(x) y_{1}^{\prime}(x)+b(x) y_{1}(x)\right] v^{\prime}(x)=f(x)\)
Dejando\(z=v^{\prime}\), vemos que tenemos la ecuación lineal de primer orden para\(z(x)\):
\[\left.a(x) y_{(} x\right) z^{\prime}(x)+\left[2 a(x) y_{1}^{\prime}(x)+b(x) y_{1}(x)\right] z(x)=f(x) \nonumber \]
Utilizar el Método de Reducción de Orden para resolver\(y^{\prime \prime}+\)\(y=\sec x .\)
Soluciones de la ecuación homogénea,\(y^{\prime \prime}+y=0\) son\(\sin x\) y\(\cos x .\) Podemos elegir cualquiera de las dos para comenzar a utilizar el Método de Reducción de Orden. Tomemos\(y_{p}=v \cos x .\) Sus derivados están dados por
\(\begin{aligned} y_{p}^{\prime} &=(v \cos x)^{\prime} \\ &=v^{\prime} \cos x-v \sin x \\ y_{p}^{\prime \prime} &=\left(v^{\prime} \cos x-v \sin x\right)^{\prime} \\ &=v^{\prime \prime} \cos x-2 v^{\prime} \sin x-v \cos x \end{aligned}\)
Sustituyendo en la ecuación no homogénea, tenemos
\(\begin{aligned} \sec x &=y_{p}^{\prime \prime}+y_{p} \\ &=v^{\prime \prime} \cos x-2 v^{\prime} \sin x-v \cos x+v \cos x \\ &=v^{\prime \prime} \cos x-2 v^{\prime} \sin x \end{aligned}\)
Dejando\(v^{\prime}=z\), tenemos la ecuación diferencial lineal de primer orden
\((\cos x) z^{\prime}-(2 \sin x) z=\sec x\)
Reescribir la ecuación como,
\(z^{\prime}-(2 \tan x) z=\sec ^{2} x\)
Multiplicando por el factor integrador,
\(\begin{aligned} \mu(x) &=-\exp \int^{x} 2 \tan \xi d \xi \\ &=-\exp 2 \ln |\sec x| \\ &=\cos ^{2} x \end{aligned}\)
obtenemos
\(\left(z \cos ^{2} x\right)^{\prime}=1\)
Integrando,
\(v^{\prime}=z=x \sec ^{2} x\)
Esto se puede integrar mediante la integración por partes (dejando\(U=x\) y\(V=\tan x)\):
\(\begin{aligned} v &=\int x \sec ^{2} x d x \\ &=x \tan x-\int \tan x d x \\ &=x \tan x-\ln |\sec x| \end{aligned}\)
Ahora tenemos suficiente para escribir la solución. La solución particular viene dada por
\(\begin{aligned} y_{p} &=v y_{1} \\ &=(x \tan x-\ln |\sec x|) \cos x \\ &=x \sin x+\cos x \ln |\cos x| \end{aligned}\)
La solución general es entonces
\(y(x)=c_{1} \cos x+c_{2} \sin x+x \sin x+\cos x \ln |\cos x|\)
Método de Variación de Parámetros
Una manera más sistemática de encontrar soluciones particulares es mediante el uso del Método de Variación de Parámetros. La derivación es un poco detallada y la solución a veces es desordenada, pero la aplicación del método es sencilla si se pueden hacer las integrales requeridas. Primero derivaremos las ecuaciones necesarias y luego haremos algunos ejemplos.
Comenzamos con la ecuación no homogénea. Supongamos que es de la forma estándar
\[a(x) y^{\prime \prime}(x)+b(x) y^{\prime}(x)+c(x) y(x)=f(x) \nonumber \]
Sabemos que la solución de la ecuación homogénea se puede escribir en términos de dos soluciones linealmente independientes, a las que llamaremos\(y_{1}(x)\) y\(y_{2}(x):\)
\(y_{h}(x)=c_{1} y_{1}(x)+c_{2} y_{2}(x)\)
Sustituyendo las constantes con funciones, entonces ya no tenemos solución a la ecuación homogénea. ¿Es posible que pudiéramos tropezar con las funciones correctas con las que reemplazar las constantes y de alguna manera terminar con\(f(x)\) cuando se insertan en el lado izquierdo de la ecuación diferencial? Resulta que podemos.
Entonces, supongamos que las constantes son reemplazadas por dos funciones desconocidas, a las que llamaremos\(c_{1}(x)\) y\(c_{2}(x)\). Este cambio de los parámetros es donde deriva el nombre del método. Así, estamos asumiendo que una solución particular toma la forma
\[y_{p}(x)=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x). \nonumber \]
Suponemos que la ecuación no homogénea tiene una solución particular de la forma\(y_{p}(x)=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x)\)
Si esto va a ser una solución, entonces la inserción en la ecuación diferencial debería hacer que la ecuación se mantenga. Para ello primero necesitaremos computar algunas derivadas.
La primera derivada viene dada por
\[y_{p}^{\prime}(x)=c_{1}(x) y_{1}^{\prime}(x)+c_{2}(x) y_{2}^{\prime}(x)+c_{1}^{\prime}(x) y_{1}(x)+c_{2}^{\prime}(x) y_{2}(x) \nonumber \]
A continuación necesitaremos la segunda derivada. Pero, esto dará ocho términos. Entonces, primero haremos una suposición simplificadora. Supongamos que los dos últimos términos se suman a cero:
\[c_{1}^{\prime}(x) y_{1}(x)+c_{2}^{\prime}(x) y_{2}(x)=0 \nonumber \]
Resulta que al final obtendremos los mismos resultados si no asumimos esto. ¡Lo importante es que funcione!
Bajo el supuesto de que la primera derivada simplifica a
\[y_{p}^{\prime}(x)=c_{1}(x) y_{1}^{\prime}(x)+c_{2}(x) y_{2}^{\prime}(x) \nonumber \]
La segunda derivada ahora solo tiene cuatro términos:
\[y_{p}^{\prime}(x)=c_{1}(x) y_{1}^{\prime \prime}(x)+c_{2}(x) y_{2}^{\prime \prime}(x)+c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x) \nonumber \]
Ahora que tenemos las derivadas, podemos insertar la conjetura en la ecuación diferencial. Así, tenemos
\[ \begin{aligned} f(x)=& a(x)\left[c_{1}(x) y_{1}^{\prime \prime}(x)+c_{2}(x) y_{2}^{\prime \prime}(x)+c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)\right] \\ &+b(x)\left[c_{1}(x) y_{1}^{\prime}(x)+c_{2}(x) y_{2}^{\prime}(x)\right] \\ &+c(x)\left[c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x)\right] \end{aligned} \label{2.64} \]
Reagrupando los términos, obtenemos
\[ \begin{aligned} f(x)=& c_{1}(x)\left[a(x) y_{1}^{\prime \prime}(x)+b(x) y_{1}^{\prime}(x)+c(x) y_{1}(x)\right] \\ &+c_{2}(x)\left[a(x) y_{2}^{\prime \prime}(x)+b(x) y_{2}^{\prime}(x)+c(x) y_{2}(x)\right] \\ &+a(x)\left[c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)\right] \end{aligned} \label{2.65} \]
Tenga en cuenta que las dos primeras filas desaparecen desde entonces\(y_{1}\) y\(y_{2}\) son soluciones del problema homogéneo. Esto deja la ecuación
\[f(x)=a(x)\left[c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)\right] \nonumber \]
que se puede reorganizar como
\[c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)=\dfrac{f(x)}{a(x)} \nonumber \]
Para resolver la ecuación diferencial\(L y=f\), asumimos\(y_{p}(x)=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x)\) para\(L y_{1,2}=0\). Entonces, uno solo necesita resolver un sistema sencillo de Ecuación\(\PageIndex{25}\).
En resumen, hemos asumido una solución particular de la forma
\(y_{p}(x)=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x)\)
Esto solo es posible si las funciones desconocidas\(c_{1}(x)\) y\(c_{2}(x)\) satisfacen el sistema de ecuaciones
\[\begin{aligned} & c_{1}^{\prime}(x) y_{1}(x)+c_{2}^{\prime}(x) y_{2}(x)=0 \\ & c_{1}^{\prime}(x) y_{1}^{\prime}(x)+c_{2}^{\prime}(x) y_{2}^{\prime}(x)=& \dfrac{f(x)}{a(x)} \end{aligned}\label{2.67} \]
Es estándar resolver este sistema para las derivadas de las funciones desconocidas y luego presentar las formas integradas. Sin embargo, uno podría comenzar fácilmente desde este sistema y resolver el sistema para cada problema encontrado.
El sistema se\(\PageIndex{25}\) puede resolver como\(\begin{aligned} c_{1}^{\prime}(x)=-\dfrac{f y_{2}}{a W\left(y_{1}, y_{2}\right)} \\ c_{1}^{\prime}(x)=\dfrac{f y_{1}}{a W\left(y_{1}, y_{2}\right)} \end{aligned}\) donde\(W\left(y_{1}, y_{2}\right)=y_{1} y_{2}^{\prime}-y_{1}^{\prime} y_{2}\) está el Wronskian. Utilizamos esta solución en la siguiente sección.
Encuentre la solución general del problema no homogéneo:\(y^{\prime \prime}-y=e^{2 x}\).
La solución general al problema homogéneo\(y_{h}^{\prime \prime}-y_{h}=0\) es
\(y_{h}(x)=c_{1} e^{x}+c_{2} e^{-x}\)
Para utilizar el Método de Variación de Parámetros, buscamos una solución de la forma
\(y_{p}(x)=c_{1}(x) e^{x}+c_{2}(x) e^{-x}\)
Encontramos las funciones desconocidas resolviendo el sistema en Ecuación\(\PageIndex{25}\), que en este caso se convierte
\[\begin{equation} \begin{aligned} &c_{1}^{\prime}(x) e^{x}+c_{2}^{\prime}(x) e^{-x}=0 \\ &c_{1}^{\prime}(x) e^{x}-c_{2}^{\prime}(x) e^{-x}=e^{2 x} \end{aligned} \end{equation}\label{2.68} \]
Sumando estas ecuaciones encontramos que
\(2 c_{1}^{\prime} e^{x}=e^{2 x} \rightarrow c_{1}^{\prime}=\dfrac{1}{2} e^{x}\)
Resolviendo para\(c_{1}(x)\) nosotros encontramos
\(c_{1}(x)=\dfrac{1}{2} \int e^{x} d x=\dfrac{1}{2} e^{x}\)
Restar las ecuaciones en el sistema rinde
\(2 c_{2}^{\prime} e^{-x}=-e^{2 x} \rightarrow c_{2}^{\prime}=-\dfrac{1}{2} e^{3 x}\)
Por lo tanto,
\(c_{2}(x)=-\dfrac{1}{2} \int e^{3 x} d x=-\dfrac{1}{6} e^{3 x}\)
La solución particular se encuentra insertando estos resultados en\(y_{p}\):
\[\begin{equation} \begin{aligned} y_{p}(x) &=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x) \\ &=\left(\dfrac{1}{2} e^{x}\right) e^{x}+\left(-\dfrac{1}{6} e^{3 x}\right) e^{-x} \\ &=\dfrac{1}{3} e^{2 x} \end{aligned} \end{equation}\label{2.69} \]
Así, tenemos la solución general del problema no homogéneo como
\(y(x)=c_{1} e^{x}+c_{2} e^{-x}+\dfrac{1}{3} e^{2 x}\)
Ahora considere el problema:\(y^{\prime \prime}+4 y=\sin x\).
La solución al problema homogéneo es
\[y_{h}(x)=c_{1} \cos 2 x+c_{2} \sin 2 x . \nonumber \]
Buscamos ahora una solución particular de la forma
\(y_{h}(x)=c_{1}(x) \cos 2 x+c_{2}(x) \sin 2 x .\)
Dejamos\(y_{1}(x)=\cos 2 x\) y\(y_{2}(x)=\sin 2 x, a(x)=1, f(x)=\sin x\) en Ecuación\(\PageIndex{25}\):
\[\begin{aligned} c_{1}^{\prime}(x) \cos 2 x+c_{2}^{\prime}(x) \sin 2 x &=0 \\ -2 c_{1}^{\prime}(x) \sin 2 x+2 c_{2}^{\prime}(x) \cos 2 x &=\sin x. \end{aligned}\label{2.71} \]
Ahora, usa tu método favorito para resolver un sistema de dos ecuaciones y dos incógnitas. En este caso, podemos multiplicar la primera ecuación por\(2 \sin 2 x\) y la segunda por\(\cos 2 x\). Al sumar las ecuaciones resultantes se eliminarán los\(c_{1}^{\prime}\) términos. Así, tenemos
\(c_{2}^{\prime}(x)=\dfrac{1}{2} \sin x \cos 2 x=\dfrac{1}{2}\left(2 \cos ^{2} x-1\right) \sin x\)
Insertando esto en la primera ecuación del sistema, tenemos
\(c_{1}^{\prime}(x)=-c_{2}^{\prime}(x) \dfrac{\sin 2 x}{\cos 2 x}=-\dfrac{1}{2} \sin x \sin 2 x=-\sin ^{2} x \cos x\)
Estos se pueden resolver fácilmente:
\(\begin{gathered} c_{2}(x)=\dfrac{1}{2} \int\left(2 \cos ^{2} x-1\right) \sin x d x=\dfrac{1}{2}\left(\cos x-\dfrac{2}{3} \cos ^{3} x\right) \\ c_{1}(x)=-\int \sin ^{x} \cos x d x=-\dfrac{1}{3} \sin ^{3} x \end{gathered}\)
El paso final para obtener la solución particular es insertar estas funciones en\(y_{p}(x)\). Esto da
\[\begin{equation} \begin{aligned} y_{p}(x) &=c_{1}(x) y_{1}(x)+c_{2}(x) y_{2}(x) \\ &=\left(-\dfrac{1}{3} \sin ^{3} x\right) \cos 2 x+\left(\dfrac{1}{2} \cos x-\dfrac{1}{3} \cos ^{3} x\right) \sin x \\ &=\dfrac{1}{3} \sin x \end{aligned}\end{equation}\label{2.72} \]
Entonces, la solución general es
\[y(x)=c_{1} \cos 2 x+c_{2} \sin 2 x+\dfrac{1}{3} \sin x \nonumber \]
2.4.5: Funciones de Green de Valor Inicial
EN ESTA SECCIÓN INVESTIGAREMOS la solución de problemas de valores iniciales que involucran ecuaciones diferenciales no homogéneas usando funciones de Green. Nuestro objetivo es resolver la ecuación diferencial no homogénea
\[a(t) y^{\prime \prime}(t)+b(t) y^{\prime}(t)+c(t) y(t)=f(t) \label{2.74} \]
sujeto a las condiciones iniciales
\(y(0)=y_{0} \quad y^{\prime}(0)=v_{0}\)
Dado que estamos interesados en problemas de valor inicial, denotaremos la variable independiente como variable de tiempo,\(t\).
La ecuación se\(\PageIndex{32}\) puede escribir de forma compacta como
\(L[y]=f\)
donde\(L\) esta el operador diferencial
\(L=a(t) \dfrac{d^{2}}{d t^{2}}+b(t) \dfrac{d}{d t}+c(t)\)
La solución es dada formalmente por
\(y=L^{-1}[f]\)
La inversa de un operador diferencial es un operador integral, que buscamos escribir en la forma
\(y(t)=\int G(t, \tau) f(\tau) d \tau\)
La función\(G(t, \tau)\) se conoce como el núcleo del operador integral y se llama la función de Green.
La historia de la función de los Verdes se remonta a 1828, cuando George Green publicó un trabajo en el que buscó soluciones de la ecuación de Poisson\(\nabla^{2} u=f\) para el potencial eléctrico\(u\) definido dentro de un volumen acotado con condiciones de límite especificadas en la superficie del volumen. Introdujo una función ahora identificada como lo que Riemann luego acuñó la “función de los Verdes”. En esta sección derivaremos el valor inicial de la función de Green para ecuaciones diferenciales ordinarias. Más adelante en el libro volveremos al valor límite de las funciones de Green y a las funciones de Green para ecuaciones diferenciales parciales.
George Green (1793-1841), físico matemático británico que tenía poca educación formal y trabajaba como molinero y panadero, publicó Un ensayo sobre la aplicación del análisis matemático a las teorías de la electricidad y el magnetismo en el que no sólo introdujo lo que ahora se conoce como la función de Green, sino que también introdujo la teoría del potencial y el teorema de Green en sus estudios de electricidad y magnetismo. Recientemente su ponencia fue publicada en Arxiv.org, ARXiv:0807.0088.
En la última sección resolvimos ecuaciones no homogéneas como Ecuación\(\PageIndex{32}\) usando el Método de Variación de Parámetros. Dejando,
\[y_{p}(t)=c_{1}(t) y_{1}(t)+c_{2}(t) y_{2}(t) \nonumber \]
encontramos que tenemos que resolver el sistema de ecuaciones
\[ \begin{aligned} &c_{1}^{\prime}(t) y_{1}(t)+c_{2}^{\prime}(t) y_{2}(t)=0 \\ &c_{1}^{\prime}(t) y_{1}^{\prime}(t)+c_{2}^{\prime}(t) y_{2}^{\prime}(t)=\dfrac{f(t)}{q(t)} \end{aligned} \label{2.76} \]
Este sistema se resuelve fácilmente para dar
\[ \begin{aligned} &c_{1}^{\prime}(t)=-\dfrac{f(t) y_{2}(t)}{a(t)\left[y_{1}(t) y_{2}^{\prime}(t)-y_{1}^{\prime}(t) y_{2}(t)\right]} \\ &c_{2}^{\prime}(t)=\dfrac{f(t) y_{1}(t)}{a(t)\left[y_{1}(t) y_{2}^{\prime}(t)-y_{1}^{\prime}(t) y_{2}(t)\right]} . \end{aligned} \label{2.77} \]
Observamos que el denominador en estas expresiones involucra lo wronskiano de las soluciones al problema homogéneo, que viene dado por el determinante
\[W\left(y_{1}, y_{2}\right)(t)=\left|\begin{array}{ll} y_{1}(t) & y_{2}(t) \\ y_{1}^{\prime}(t) & y_{2}^{\prime}(t) \end{array}\right| \nonumber \]
Cuando\(y_{1}(t)\) y\(y_{2}(t)\) son linealmente independientes, entonces el Wronskian no es cero y se nos garantiza una solución al sistema anterior.
Entonces, después de una integración, encontramos los parámetros como
\[ \begin{aligned} c_{1}(t) &=-\int_{t_{0}}^{t} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \\ c_{2}(t) &=\int_{t_{1}}^{t} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau \end{aligned} \label{2.79} \]
donde\(t_{0}\) y\(t_{1}\) son constantes arbitrarias a determinar a partir de las condiciones iniciales.
Por lo tanto, la solución particular de\(Equation \(\PageIndex{32}\)\) puede escribirse como
\[ y_{p}(t)=y_{2}(t) \int_{t_{1}}^{t} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau-y_{1}(t) \int_{t_{0}}^{t} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
Comenzamos con la solución particular Ecuación\(\PageIndex{37}\) de la ecuación diferencial no homogénea Ecuación\(\PageIndex{32}\). Esto se puede combinar con la solución general del problema homogéneo para dar la solución general de la ecuación diferencial no homogénea:
\[y_{p}(t)=c_{1} y_{1}(t)+c_{2} y_{2}(t)+y_{2}(t) \int_{t_{1}}^{t} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau-y_{1}(t) \int_{t_{0}}^{t} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
Sin embargo, una elección adecuada de\(t_{0}\) y se\(t_{1}\) puede encontrar para que no sea necesario escribir explícitamente la solución al problema homogéneo,\(c_{1} y_{1}(t)+c_{2} y_{2}(t) .\) Sin embargo, establecer la solución en esta forma nos permitirá utilizar\(t_{0}\) y \(t_{1}\)para determinar soluciones particulares que satisfaga ciertas condiciones homogéneas. En particular, mostraremos que la ecuación se\(\PageIndex{38}\) puede escribir en la forma
\[y(t)=c_{1} y_{1}(t)+c_{2} y_{2}(t)+\int_{0}^{t} G(t, \tau) f(\tau) d \tau \nonumber \]
donde la función\(G(t, \tau)\) será identificada como la función del Verde.
El objetivo es desarrollar la técnica de función de Green para resolver el problema de valor inicial
\[a(t) y^{\prime \prime}(t)+b(t) y^{\prime}(t)+c(t) y(t)=f(t), \quad y(0)=y_{0}, \quad y^{\prime}(0)=v_{0} \nonumber \]
Primero notamos que podemos resolver este problema de valor inicial resolviendo dos problemas de valor inicial separados. Suponemos que la solución del problema homogéneo satisface las condiciones iniciales originales:
\[a(t) y_{h}^{\prime \prime}(t)+b(t) y_{h}^{\prime}(t)+c(t) y_{h}(t)=0, \quad y_{h}(0)=y_{0}, \quad y_{h}^{\prime}(0)=v_{0} \nonumber \]
Entonces asumimos que la solución particular satisface el problema
\[a(t) y_{p}^{\prime \prime}(t)+b(t) y_{p}^{\prime}(t)+c(t) y_{p}(t)=f(t), \quad y_{p}(0)=0, \quad y_{p}^{\prime}(0)=0 \nonumber \]
Como la ecuación diferencial es lineal, entonces sabemos que
\(y(t)=y_{h}(t)+y_{p}(t)\)
es una solución de la ecuación no homogénea. Además, esta solución satisface las condiciones iniciales:
\(\begin{aligned} &y(0)=y_{h}(0)+y_{p}(0)=y_{0}+0=y_{0} \\ &y^{\prime}(0)=y_{h}^{\prime}(0)+y_{p}^{\prime}(0)=v_{0}+0=v_{0} \end{aligned}\)
Por lo tanto, solo necesitamos enfocarnos en encontrar una solución particular que satisfaga condiciones iniciales homogéneas. Esto se hará encontrando valores para\(t_{0}\) y\(t_{1}\) en Ecuación\(\PageIndex{37}\) que satisfagan las condiciones iniciales homogéneas,\(y_{p}(0)=0\) y\(y_{p}^{\prime}(0)=0\).
Primero,\(y_{p}(0)=0 .\) consideramos Tenemos
\[y_{p}(0)=y_{2}(0) \int_{t_{1}}^{0} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau-y_{1}(0) \int_{t_{0}}^{0} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
Aquí,\(y_{1}(t)\) y\(y_{2}(t)\) se toman como cualquier solución de la ecuación diferencial homogénea. Supongamos eso\(y_{1}(0)=0\) y\(y_{2} \neq(0)=0 .\) Entonces, tenemos
\[y_{p}(0)=y_{2}(0) \int_{t_{1}}^{0} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
Podemos forzar\(y_{p}(0)=0\) si nos fijamos\(t_{1}=0\).
Ahora, consideramos\(y_{p}^{\prime}(0)=0\). Primero diferenciamos la solución y encontramos que
\[y_{p}^{\prime}(t)=y_{2}^{\prime}(t) \int_{0}^{t} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau-y_{1}^{\prime}(t) \int_{t_{0}}^{t} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
ya que las contribuciones de diferenciar las integrales se cancelarán. Evaluando este resultado en\(t=0\), tenemos
\[y_{p}^{\prime}(0)=-y_{1}^{\prime}(0) \int_{t_{0}}^{0} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \nonumber \]
Suponiendo eso\(y_{1}^{\prime}(0) \neq 0\), podemos establecer\(t_{0}=0\).
Así, hemos encontrado que
\[ \begin{aligned} y_{p}(x) &=y_{2}(t) \int_{0}^{t} \dfrac{f(\tau) y_{1}(\tau)}{a(\tau) W(\tau)} d \tau-y_{1}(t) \int_{0}^{t} \dfrac{f(\tau) y_{2}(\tau)}{a(\tau) W(\tau)} d \tau \\ &=\int_{0}^{t}\left[\dfrac{y_{1}(\tau) y_{2}(t)-y_{1}(t) y_{2}(\tau)}{a(\tau) W(\tau)}\right] f(\tau) d \tau \end{aligned}\label{2.89} \]
Este resultado está en la forma correcta y podemos identificar el valor temporal, o inicial, la función de Green. Entonces, la solución particular se da como
\[y_{p}(t)=\int_{0}^{t} G(t, \tau) f(\tau) d \tau \nonumber \]
donde el valor inicial La función de Green se define como
\(G(t, \tau)=\dfrac{y_{1}(\tau) y_{2}(t)-y_{1}(t) y_{2}(\tau)}{a(\tau) W(\tau)}\)
Resumimos
Solución de IVP usando la función de Green
La solución del problema del valor inicial,
\(a(t) y^{\prime \prime}(t)+b(t) y^{\prime}(t)+c(t) y(t)=f(t), \quad y(0)=y_{0}, \quad y^{\prime}(0)=v_{0}\)
toma la forma
\[y(t)=y_{h}(t)+\int_{0}^{t} G(t, \tau) f(\tau) d \tau \nonumber \]
donde
\[G(t, \tau)=\dfrac{y_{1}(\tau) y_{2}(t)-y_{1}(t) y_{2}(\tau)}{a(\tau) W(\tau)} \nonumber \]
es la función de Green y\(y_{1}, y_{2}, y_{h}\) son soluciones de la ecuación homogénea satisfaciendo
\(y_{1}(0)=0, y_{2}(0) \neq 0, y_{1}^{\prime}(0) \neq 0, y_{2}^{\prime}(0)=0, y_{h}(0)=y_{0}, y_{h}^{\prime}(0)=v_{0}\)
Resolver el problema del oscilador forzado
\(x^{\prime \prime}+x=2 \cos t, \quad x(0)=4, \quad x^{\prime}(0)=0\)
Primero resolvemos el problema homogéneo con condiciones iniciales no homogéneas:
\[x_{h}^{\prime \prime}+x_{h}=0, \quad x_{h}(0)=4, \quad x_{h}^{\prime}(0)=0 \nonumber \]
Se ve fácilmente que la solución es\(x_{h}(t)=4 \cos t\).
A continuación, construimos la función del Verde. Necesitamos dos soluciones linealmente independientes,\(y_{1}(x), y_{2}(x)\), a la ecuación diferencial homogénea satisfaciendo diferentes condiciones homogéneas,\(y_{1}(0)=0\) y\(y_{2}^{\prime}(0)=0 .\) Las soluciones más simples son\(y_{1}(t)=\sin t\) y\(y_{2}(t)=\cos t .\) El Wronskian se encuentra como
\(W(t)=y_{1}(t) y_{2}^{\prime}(t)-y_{1}^{\prime}(t) y_{2}(t)=-\sin ^{2} t-\cos ^{2} t=-1\)
Ya que\(a(t)=1\) en este problema, calculamos la función de Green,
\[\begin{equation} \begin{aligned} G(t, \tau) &=\dfrac{y_{1}(\tau) y_{2}(t)-y_{1}(t) y_{2}(\tau)}{a(\tau) W(\tau)} \\ &=\sin t \cos \tau-\sin \tau \cos t \\ &=\sin (t-\tau) \end{aligned}\end{equation}\label{2.93} \]
Tenga en cuenta que la función del Verde depende de\(t-\tau\). Si bien esto es útil en algunos contextos, utilizaremos la forma expandida a la hora de llevar a cabo la integración.
Ahora podemos determinar la solución particular de la ecuación diferencial no homogénea. Tenemos
\[\begin{equation} \begin{aligned} x_{p}(t) &=\int_{0}^{t} G(t, \tau) f(\tau) d \tau \\ &=\int_{0}^{t}(\sin t \cos \tau-\sin \tau \cos t)(2 \cos \tau) d \tau \\ &=2 \sin t \int_{0}^{t} \cos ^{2} \tau d \tau-2 \cos t \int_{0}^{t} \sin \tau \cos \tau d \tau \\ &=2 \sin t\left[\dfrac{\tau}{2}+\dfrac{1}{2} \sin 2 \tau\right]_{0}^{t}-2 \cos t\left[\dfrac{1}{2} \sin ^{2} \tau\right]_{0}^{t} \\ &=t \sin t \end{aligned} \end{equation}\label{2.94} \]
Por lo tanto, la solución del problema no homogéneo es la suma de la solución del problema homogéneo y esta solución particular:\(x(t)=4 \cos t+t \sin t\)