6.2.2: Circuitos

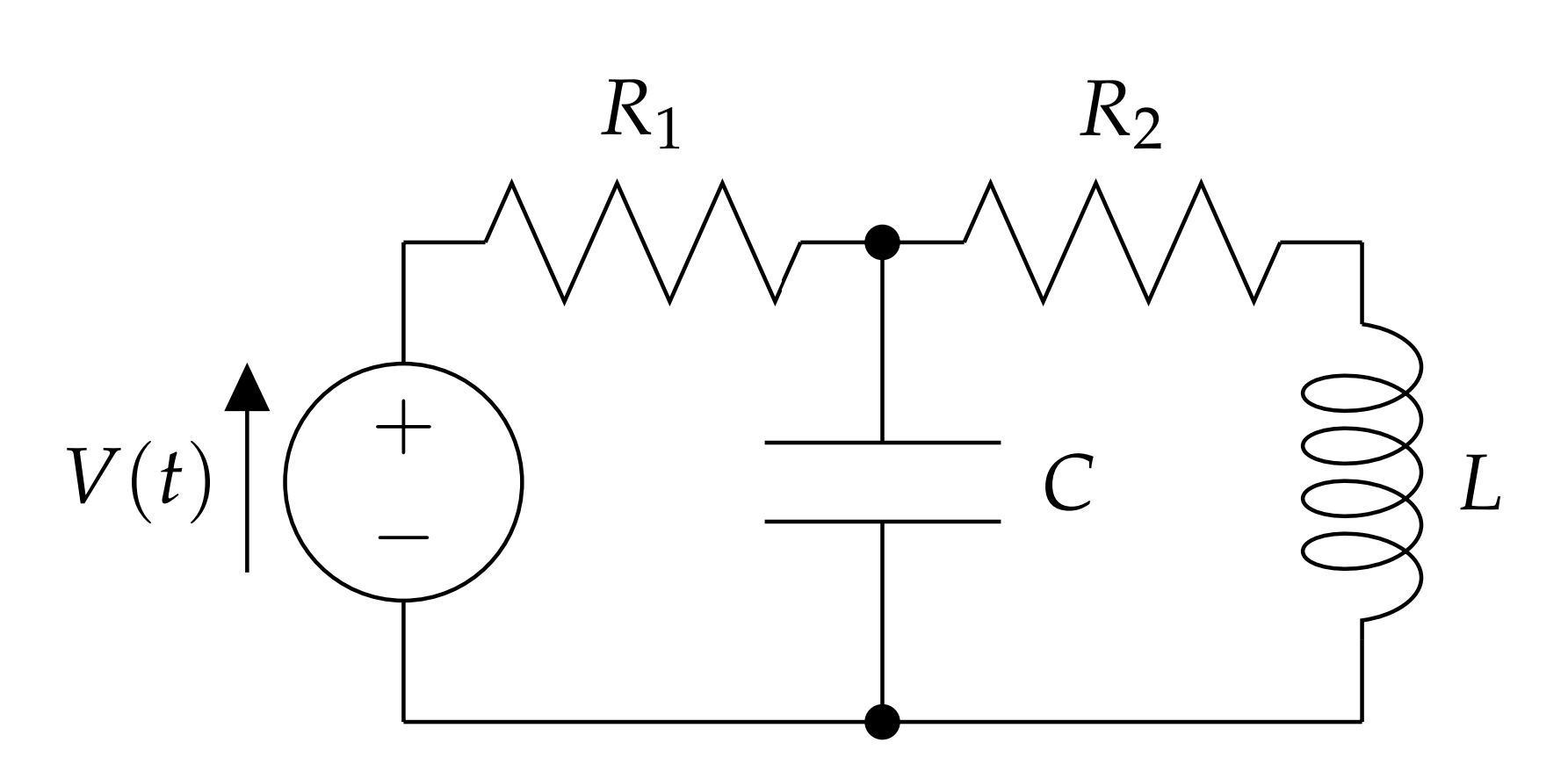
EN EL ÚLTIMO CAPÍTULO INVESTIGAMOS CIRCUITOS LRC SERIES SIMPLES. Los circuitos más complicados son posibles al observar conexiones en paralelo, u otras combinaciones, de resistencias, condensadores e inductores. Esto da como resultado varias ecuaciones para cada bucle en el circuito, lo que lleva a sistemas más grandes de ecuaciones diferenciales. Un ejemplo de otra configuración de circuito se muestra en la Figura\(\PageIndex{1}\). Esto no es un problema que pueda cubrirse en el curso de física de primer año.

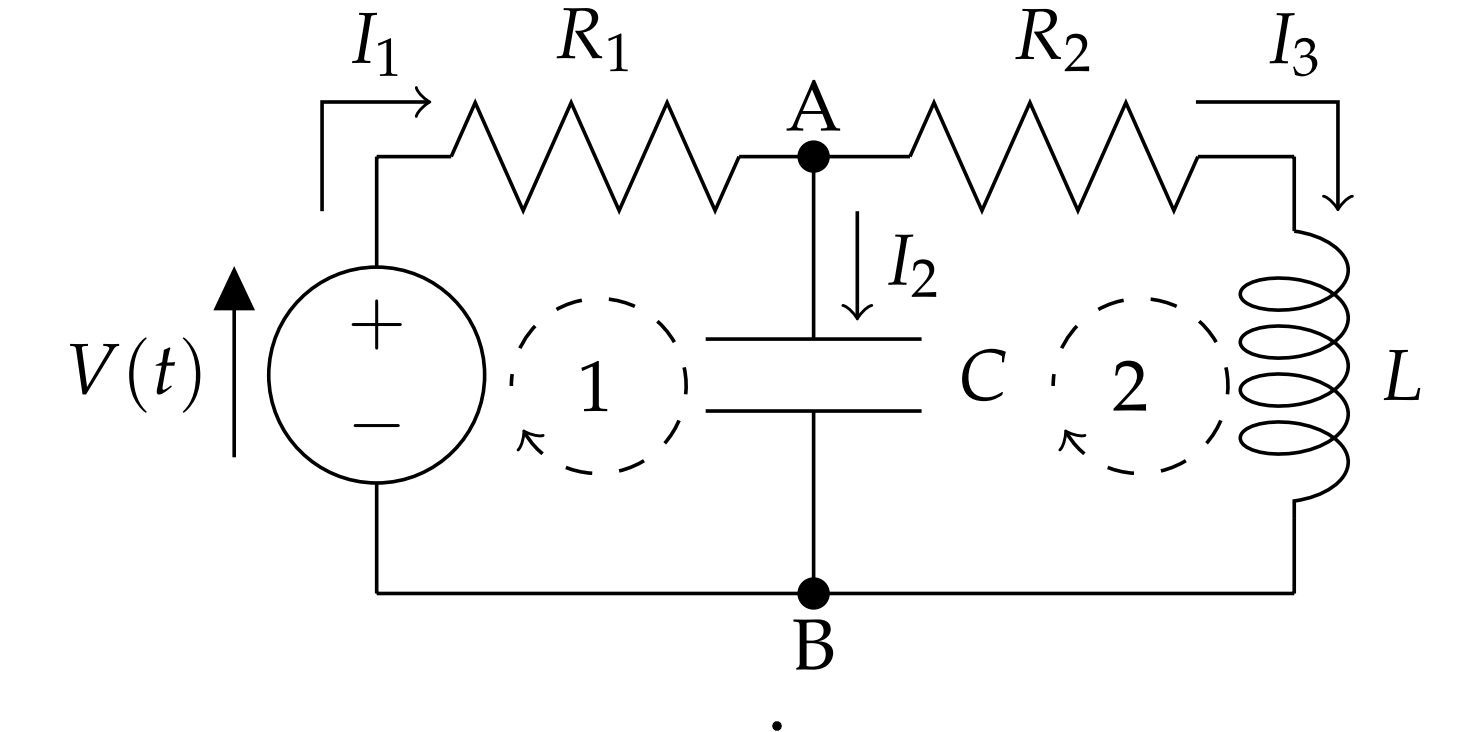
Hay dos bucles, indicados en la Figura\(\PageIndex{2}\) como atravesados en el sentido de las agujas del reloj. Para cada bucle necesitamos aplicar la Regla de Loop de Kirchoff. Hay tres corrientes orientadas, etiquetadas\(I_{i}, i=1,2,3\). Correspondiente a cada corriente hay una carga cambiante, de\(q_{i}\) tal manera que

\[I_{i}=\dfrac{d q_{i}}{d t}, \quad i=1,2,3 \nonumber \]

Tenemos para el bucle uno

\[I_1 R_1 + \dfrac{q_2}{C} = V(t) \nonumber \]

y para el bucle dos

\[I_{3} R_{2}+L \dfrac{d I_{3}}{d t}=\dfrac{q_{2}}{C} . \nonumber \]

Figura\(\PageIndex{1}\): Un circuito con dos bucles que contiene varios elementos de circuito diferentes.

Figura\(\PageIndex{2}\): El circuito paralelo anterior con las direcciones indicadas para atravesar los bucles en las Leyes de Kirchoff.

Hay tres funciones desconocidas para el cargo. Una vez que conocemos las funciones de carga, la diferenciación dará lugar a las tres corrientes. Sin embargo, sólo tenemos dos ecuaciones. Necesitamos una tercera ecuación. Esta ecuación se encuentra a partir de la Regla Point (Junction) de Kirchoff.

Considera los puntos A y B de la Figura\(\PageIndex{2}\). Cualquier cargo (corriente) que ingrese a estos cruces debe ser el mismo que el cargo total (actual) que sale de los cruces. Por punto\(A\) tenemos

\[I_{1}=I_{2}+I_{3} \nonumber \]

O

\[\dot{q}_{1}=\dot{q}_{2}+\dot{q}_{3} \nonumber \]

Ecuaciones\(\PageIndex{1}, \PageIndex{2}\), y\(\PageIndex{4}\) formar un sistema acoplado de ecuaciones diferenciales para este problema. Hay ambos derivados de primer y segundo orden involucrados. Podemos escribir todo el sistema en términos de cargos como

\[ \begin{array}{r} R_{1} \dot{q}_{1}+\dfrac{q_{2}}{C}=V(t) \\ R_{2} \dot{q}_{3}+L \ddot{q}_{3}=\dfrac{q_{2}}{C} \\ \dot{q}_{1}=\dot{q}_{2}+\dot{q}_{3} . \end{array} \label{6.49} \]

La cuestión es si, o no, podemos escribir esto como un sistema de ecuaciones diferenciales de primer orden. Dado que solo hay una derivada de segundo orden, podemos introducir la nueva variable\(q_{4}=\dot{q}_{3}\). La primera ecuación se puede resolver para\(\dot{q}_{1}\). La tercera ecuación se puede resolver\(\dot{q}_{2}\) con sustituciones apropiadas para los otros términos. \(\dot{q}_{3}\)se obtiene a partir de la definición de\(q_{4}\) y la segunda ecuación se puede resolver para\(\ddot{q}_{3}\) y realizar sustituciones para obtener el sistema

\[\begin{aligned} \dot{q}_{1} &=\dfrac{V}{R_{1}}-\dfrac{q_{2}}{R_{1} C} \\ \dot{q}_{2} &=\dfrac{V}{R_{1}}-\dfrac{q_{2}}{R_{1} C}-q_{4} \\ \dot{q}_{3} &=q_{4} \\ \dot{q}_{4} &=\dfrac{q_{2}}{L C}-\dfrac{R_{2}}{L} q_{4} . \end{aligned} \nonumber \]

Entonces, tenemos un sistema no homogéneo de ecuaciones diferenciales de primer orden.