6.2.3: Problemas de mezcla
- Page ID
- 119607
Hay muchos tipos de problemas de mezcla. Tales problemas son estándar en un primer curso sobre ecuaciones diferenciales como ejemplos de ecuaciones diferenciales de primer orden. Por lo general, estos ejemplos consisten en un tanque de salmuera, agua que contiene una cantidad específica de sal con agua pura entrando y saliendo la mezcla, o el flujo de un contaminante dentro o fuera de un lago. Primero vimos tales problemas en el Capítulo\(1 .\)
En general se tiene un caudal de cierta concentración de mezcla entrando en una región y una mezcla que sale de la región. El objetivo es determinar la cantidad de cosas que hay en la región en un momento dado. Esto se rige por la ecuación
\[\text{Rate of change of substance} = \text{Rate In} - \text{Rate Out}. \nonumber \]
Esto puede generalizarse al caso de dos tanques interconectados. Daremos un ejemplo, pero primero revisamos el problema de un solo tanque del Capítulo\(1 .\)
Un tanque de 50 galones de agua pura tiene una mezcla de salmuera con concentración de 2 libras por galón entrando a razón de 5 galones por minuto. [Ver Figura\(\PageIndex{1}\).] Al mismo tiempo, los contenidos bien mezclados drenan a razón de 5 galones por minuto. Encuentra la cantidad de sal en el tanque a la vez\(t .\) En todos esos problemas se supone que la solución está bien mezclada en cada instante del tiempo.
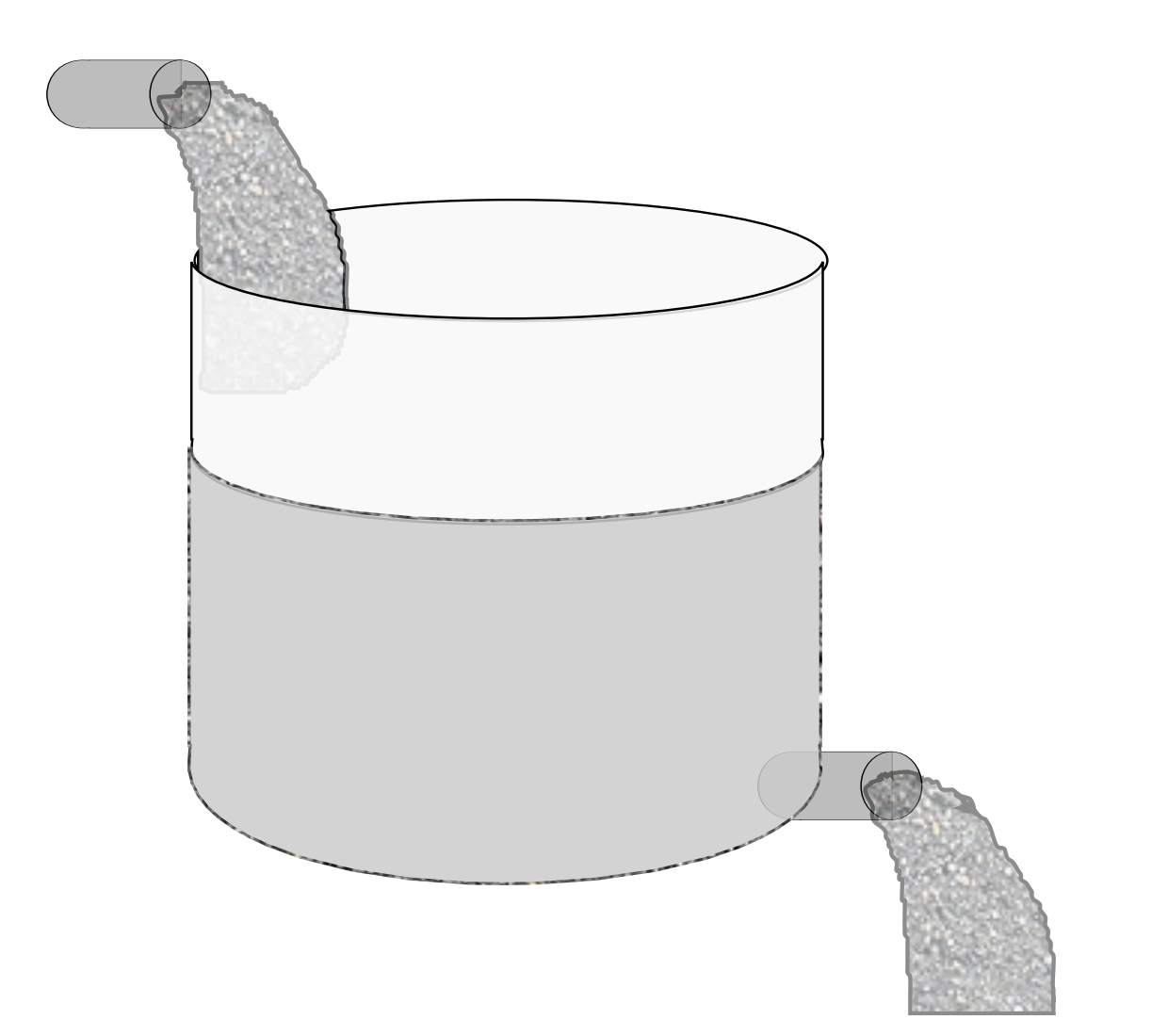
Dejar\(x(t)\) ser la cantidad de sal a la vez\(t\). Entonces la velocidad a la que aumenta la sal en el tanque se debe a la cantidad de sal que ingresa al tanque menos que la que sale del tanque. Para averiguar estas tarifas, se nota que\(d x / d t\) tiene unidades de libras por minuto. La cantidad de sal que entra por minuto viene dada por el producto de la concentración entrante multiplicada por la velocidad a la que entra la salmuera. Esto da las unidades correctas:
\[\left(2 \dfrac{\text { pounds }}{\text { gal }}\right)\left(5 \dfrac{\text { gal }}{\text { min }}\right)=10 \dfrac{\text { pounds }}{\text { min }}. \nonumber \]
Del mismo modo, se puede determinar la tasa de salida como
\[\left(\dfrac{x \text { pounds }}{50 \text { gal }}\right)\left(5 \dfrac{\text { gal }}{\text { min }}\right)=\dfrac{x}{10} \dfrac{\text { pounds }}{\text { min }} \nonumber \]
Así, tenemos
\[\dfrac{d x}{d t}=10-\dfrac{x}{10} \nonumber \]
Esta ecuación se resuelve fácilmente usando los métodos para ecuaciones de primer orden.
Uno tiene dos tanques conectados entre sí, etiquetados\(\operatorname{tank} X\) y\(\operatorname{tank} Y\), como se muestra en la Figura\(\PageIndex{2}\).
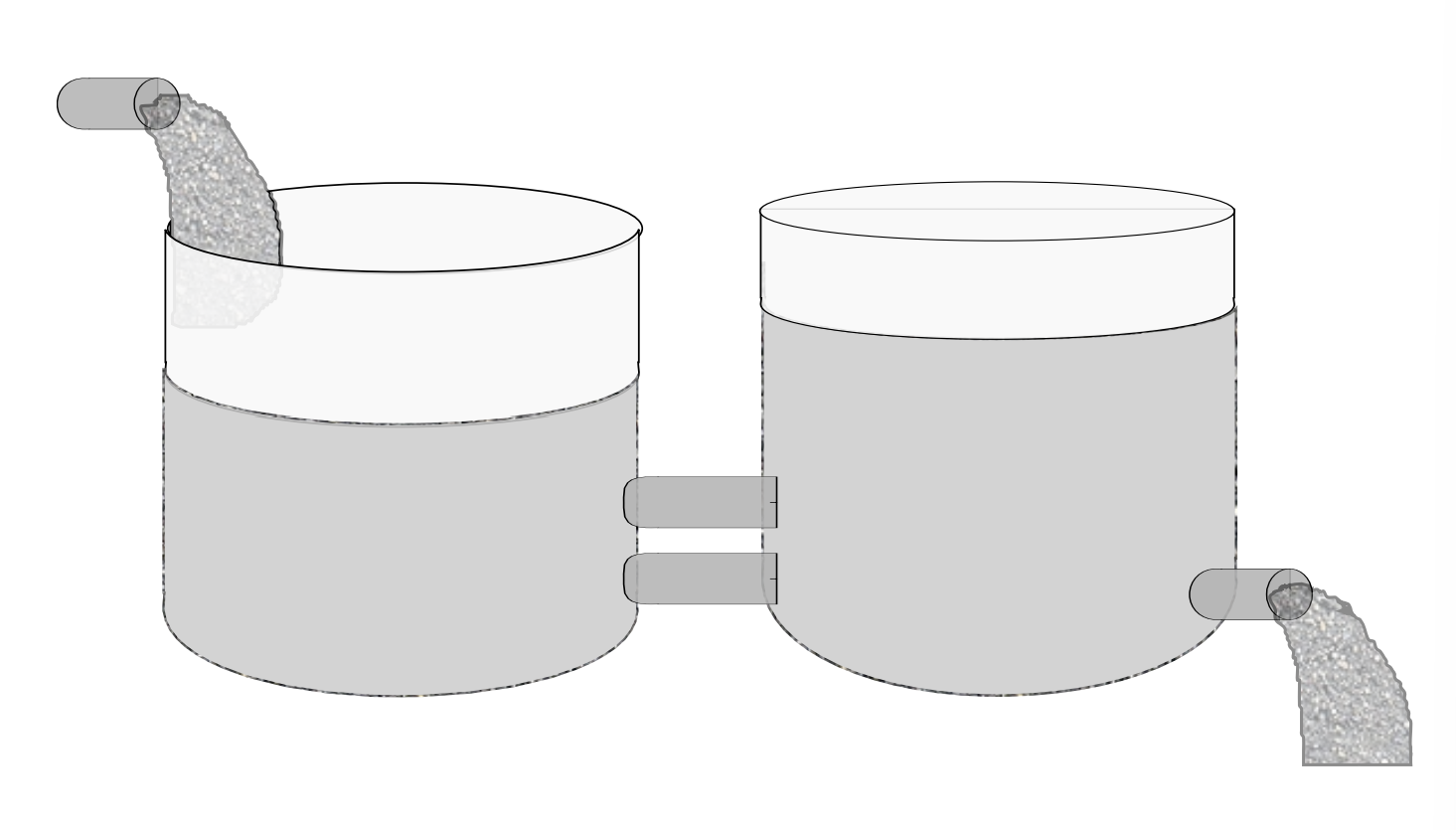
Dejar que el tanque X inicialmente tenga 100 galones de salmuera hechos con 100 libras de sal. El Tanque Y inicialmente tiene 100 galones de agua pura. El agua pura se\(X\) bombea al tanque a una velocidad de\(2.0\) galones por minuto. Parte de la mezcla de salmuera y agua pura fluye\(Y\) al tanque a 3 galones por minuto. Para mantener los niveles del tanque iguales, un galón de la\(Y\) mezcla fluye de nuevo\(\tan \mathrm{k} X\) a una velocidad de un galón por minuto y 2.0 galones por minuto drena. Encuentra la cantidad de sal en un momento dado en los tanques. ¿Qué sucede durante un largo periodo de tiempo?
En este problema configuramos dos ecuaciones. Dejar\(x(t)\) ser la cantidad de sal adentro\(\operatorname{tank} X\) y\(y(t)\) la cantidad de sal en el tanque\(Y\). Nuevamente, analizamos cuidadosamente las tasas de entrada y salida de cada tanque para establecer el sistema de ecuaciones diferenciales. Obtenemos el sistema
\[ \begin{aligned} \dfrac{d x}{d t} &=\dfrac{y}{100}-\dfrac{3 x}{100} \\ \dfrac{d y}{d t} &=\dfrac{3 x}{100}-\dfrac{3 y}{100} \end{aligned} \label{6.50} \]
Se trata de un sistema de coeficientes constantes lineales y homogéneos de dos ecuaciones de primer orden, que sabemos resolver. La forma matricial del sistema viene dada por
\[\dot{\mathbf{x}}=\left(\begin{array}{cc} -\dfrac{3}{100} & \dfrac{1}{100} \\ \dfrac{3}{100} & -\dfrac{3}{100} \end{array}\right) \mathbf{x}, \quad \mathbf{x}(0)=\left(\begin{array}{c} 100 \\ 0 \end{array}\right)\nonumber \]
Los valores propios para el problema vienen dados por\(\lambda=-3 \pm \sqrt{3}\) y los vectores propios son
\[\left(\begin{array}{c} 1 \\ \pm \sqrt{3} \end{array}\right) \nonumber \]
Dado que los valores propios son reales y distintos, la solución general se anota fácilmente:
\[\mathbf{x}(t)=c_{1}\left(\begin{array}{c} 1 \\ \sqrt{3} \end{array}\right) e^{(-3+\sqrt{3}) t}+c_{2}\left(\begin{array}{c} 1 \\ -\sqrt{3} \end{array}\right) e^{(-3-\sqrt{3}) t} \nonumber \]
Por último, necesitamos satisfacer las condiciones iniciales. Entonces,
\[\mathbf{x}(0)=c_{1}\left(\begin{array}{c} 1 \\ \sqrt{3} \end{array}\right)+c_{2}\left(\begin{array}{c} 1 \\ -\sqrt{3} \end{array}\right)=\left(\begin{array}{c} 100 \\ 0 \end{array}\right),\nonumber \]
o
\[c_{1}+c_{2}=100, \quad\left(c_{1}-c_{2}\right) \sqrt{3}=0.\nonumber \]
Entonces,\(c_{2}=c_{1}=50\). La solución final es
\[\mathbf{x}(t)=50\left(\left(\begin{array}{c} 1 \\ \sqrt{3} \end{array}\right) e^{(-3+\sqrt{3}) t}+\left(\begin{array}{c} 1 \\ -\sqrt{3} \end{array}\right) e^{(-3-\sqrt{3}) t}\right),\nonumber \]
o
\[ \begin{aligned} &x(t)=50\left(e^{(-3+\sqrt{3}) t}+e^{(-3-\sqrt{3}) t}\right) \\ &y(t)=50 \sqrt{3}\left(e^{(-3+\sqrt{3}) t}-e^{(-3-\sqrt{3}) t}\right) . \end{aligned} \label{6.51} \]


