7.5: La estabilidad de los puntos fijos en sistemas no lineales
- Page ID
- 119682
A continuación investigamos la estabilidad de las soluciones de equilibrio del péndulo no lineal que encontramos por primera vez en la sección 2.3.2. En el camino desarrollaremos algunos métodos básicos para estudiar la estabilidad de los equilibrios en sistemas no lineales en general.
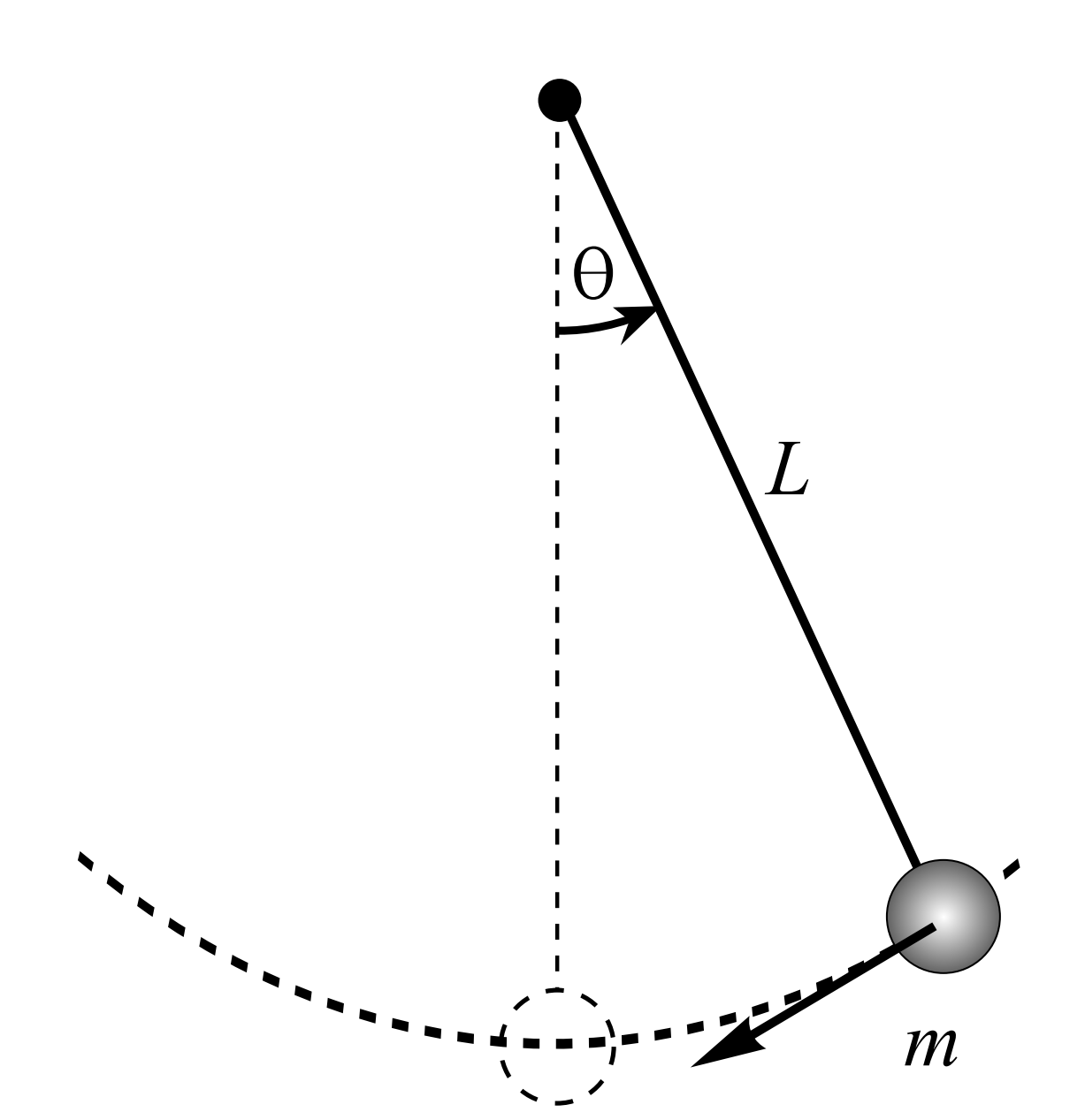
Recordemos que la derivación de la ecuación del péndulo se basó en una simple masa puntual\(m\) colgada de una cuerda de longitud\(L\) de algún soporte como se muestra en la Figura\(\PageIndex{1}\). Uno tira de la masa hacia atrás a algún ángulo inicial\(\theta_{0}\),, y la libera. El objetivo es encontrar la posición angular en función del tiempo,\(\theta(t)\).
En el Capítulo 2 derivamos la ecuación del péndulo no lineal,
\[L \ddot{\theta}+g \sin \theta=0 \nonumber \]
Hay varias variaciones de la Ecuación\(\PageIndex{1}\) que hemos utilizado en este texto. El primero es el péndulo lineal, el cual se obtuvo mediante una aproximación de ángulo pequeño,
\[L \ddot{\theta}+g \theta=0 \nonumber \]
También hicimos que el sistema fuera más realista al agregar amortiguación y forzamiento. Una variedad de estos problemas de oscilación se resumen en la siguiente tabla.
- Péndulo no lineal:\(L \ddot{\theta}+g \sin \theta=0\).
- Péndulo no lineal amortiguado:\(L \ddot{\theta}+b \dot{\theta}+g \sin \theta=0\).
- Péndulo Lineal:\(L \ddot{\theta}+g \theta=0\).
- Péndulo Lineal Amortiguado:\(L \ddot{\theta}+b \dot{\theta}+g \theta=0\).
- Péndulo no lineal amortiguado forzado:\(L \ddot{\theta}+b \dot{\theta}+g \sin \theta=F \cos \omega t\).
- Péndulo Lineal Amortiguado Forzado:\(L \ddot{\theta}+b \dot{\theta}+g \theta=F \cos \omega t\).
Hay dos sistemas simples que consideraremos, el péndulo lineal amortiguado, en la forma
\[x^{\prime \prime}+b x^{\prime}+\omega^{2} x=0 \nonumber \]
y el péndulo no lineal amortiguado, en la forma
\[x^{\prime \prime}+b x^{\prime}+\omega^{2} \sin x=0 \nonumber \]
Estas son ecuaciones diferenciales de segundo orden y se pueden emitir como un sistema de dos ecuaciones diferenciales de primer orden usando los métodos del Capítulo\(6 .\)
La ecuación lineal se puede escribir como
\[ \begin{aligned} &x^{\prime}=y \\ &y^{\prime}=-b y-\omega^{2} x \end{aligned} \label{7.13} \]
Este sistema tiene sólo una solución de equilibrio,\(x=0, y=0\).
El péndulo no lineal amortiguado toma la forma
\[ \begin{aligned} x^{\prime} &=y \\ y^{\prime} &=-b y-\omega^{2} \sin x \end{aligned} \label{7.14} \]
Este sistema también tiene la solución de equilibrio\(x=0, y=0\). Sin embargo, en realidad hay un número infinito de soluciones. Los equilibrios se determinan a partir de
\[y=0 \text { and }-b y-\omega^{2} \sin x=0 \nonumber \]
Estas ecuaciones implican que\(y=0\) y\(\sin x=0\). Hay un número infinito de soluciones a esta última ecuación:\(x=n \pi, n=0, \pm 1, \pm 2, \ldots\). Entonces, este sistema tiene un número infinito de equilibrios,\((n \pi, 0), n=0, \pm 1, \pm 2, \ldots\)
El siguiente paso es determinar la estabilidad de las soluciones de equilibrio de estos sistemas. Esto se puede lograr tal como lo habíamos hecho para las ecuaciones de primer orden. Para ello necesitamos una teoría más general para los sistemas no lineales. Entonces, desarrollaremos la maquinaria necesaria.
Comenzamos con el sistema\(n\) -dimensional
\[\mathbf{x}^{\prime}=\mathbf{f}(\mathbf{x}), \quad \mathbf{x} \in \mathrm{R}^{n} \nonumber \]
Aquí\(\mathbf{f}: \mathrm{R}^{n} \rightarrow \mathrm{R}^{n}\) hay un mapeo de\(\mathrm{R}^{n}\) a\(\mathrm{R}^{n}\). Definimos las soluciones de equilibrio, o puntos fijos, de este sistema como los puntos\(\mathbf{x}^{*}\) satisfactorios\(f(x^{*}) =0\).
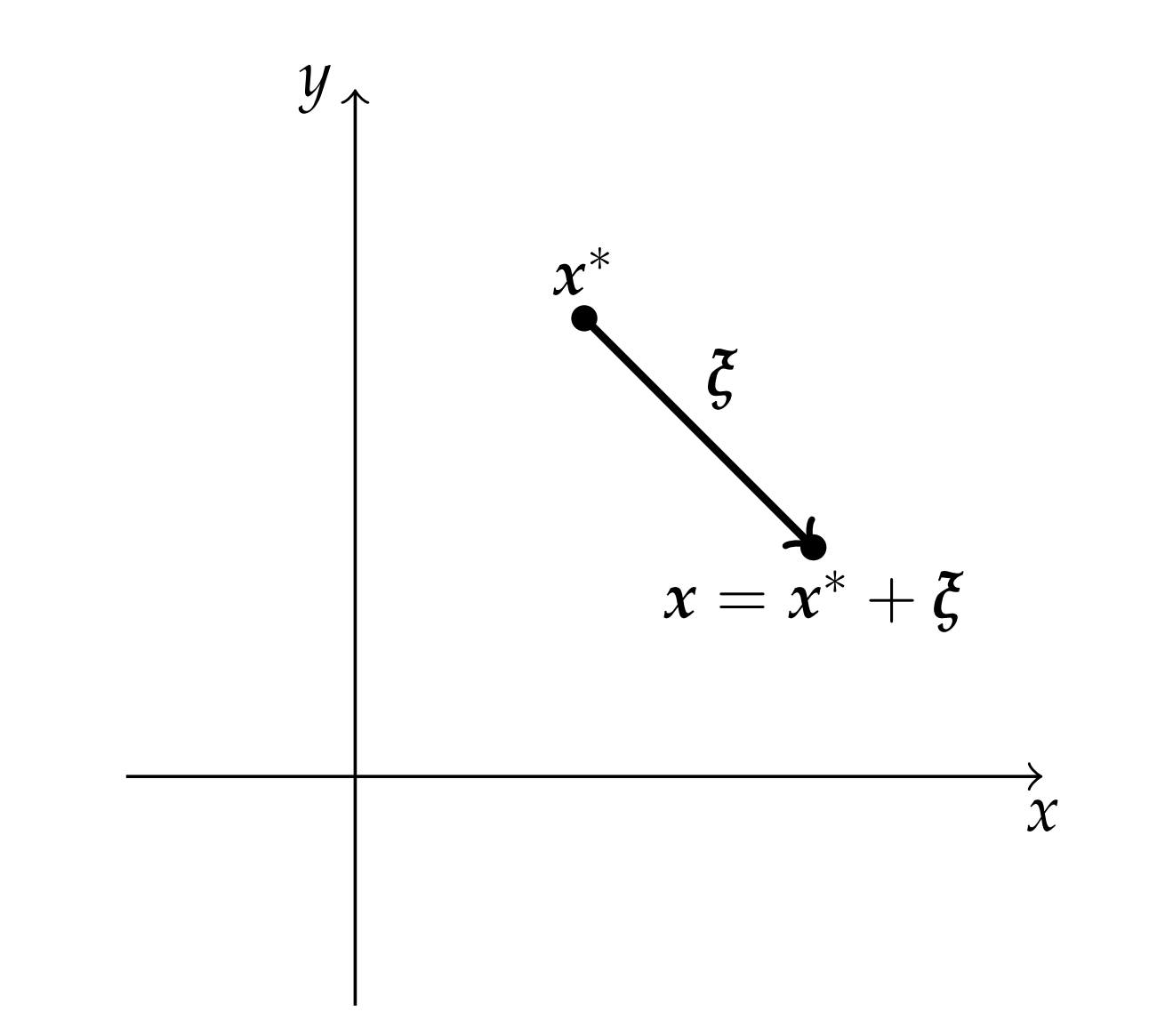
(Análisis de estabilidad lineal de sistemas). Ahora se determinará la estabilidad en la vecindad de los equilibrios. Nos interesa lo que sucede con las soluciones del sistema con condiciones iniciales comenzando cerca de un punto fijo. Representaremos un punto general en el plano, que está cerca del punto fijo, en la forma\(\mathbf{x}=\mathbf{x}^{*}+\xi\). Observamos que la longitud de\(\xi\) da una indicación de lo cerca que estamos del punto fijo. Entonces, consideramos que inicialmente,\(|\xi| \ll 1\).
A medida que el sistema evolucione,\(\xi\) va a cambiar. El cambio\(\xi\) en el tiempo se rige a su vez por un sistema de ecuaciones. Podemos aproximar esta evolución de la siguiente manera. En primer lugar, observamos que
\[\mathbf{x}^{\prime}=\xi^{\prime}\nonumber \]
A continuación, tenemos que
\[\mathbf{x}=\mathbf{x}^{*}+\xi\nonumber \]
Podemos expandir el lado derecho sobre el punto fijo usando una versión multidimensional del Teorema de Taylor. Así, tenemos que
\[\mathbf{f}\left(\mathbf{x}^{*}+\xi\right)=\mathbf{f}\left(\mathbf{x}^{*}\right)+D \mathbf{f}\left(\mathbf{x}^{*}\right) \xi+O\left(|\xi|^{2}\right) \nonumber \]
(La matriz jacobiana). Aquí\(D \mathbf{f}(\mathbf{x})\) está la matriz jacobiana, definida como
\[D \mathbf{f}\left(\mathbf{x}^{*}\right) \equiv\left(\begin{array}{cccc} \dfrac{\partial f_{1}}{\partial x_{1}} & \dfrac{\partial f_{1}}{\partial x_{2}} & \cdots & \dfrac{\partial f_{1}}{\partial x_{n}} \\ \dfrac{\partial f_{2}}{\partial x_{1}} & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \vdots \\ \dfrac{\partial f_{n}}{\partial x_{1}} & \cdots & \cdots & \dfrac{\partial f_{n}}{\partial x_{n}} \end{array}\right) \nonumber. \nonumber \]
Señalando que\(\mathbf{f}\left(\mathbf{x}^{*}\right)=\mathbf{0}\), entonces tenemos que Sistema\(\PageIndex{6}\) se convierte
\[\xi^{\prime} \approx D \mathbf{f}\left(\mathbf{x}^{*}\right) \xi \nonumber \]
Es esta ecuación la que describe el comportamiento del sistema cerca del punto fijo. Al igual que con las ecuaciones de primer orden, decimos que Sistema\(\PageIndex{6}\) ha sido linealizado o que la Ecuación\(\PageIndex{7}\) es la linealización de Sistema\(\PageIndex{6}\).
(Linealización del sistema\(\mathbf{x}^{\prime}=\mathbf{f}(\mathbf{x})\)). La estabilidad del punto de equilibrio del sistema no lineal se reduce ahora a analizar el comportamiento del sistema linealizado dado por la Ecuación\(\PageIndex{7}\). Podemos utilizar los métodos de los dos últimos capítulos para investigar los valores propios de la matriz jacobiana evaluados en cada punto de equilibrio. Demostraremos este procedimiento con varios ejemplos.
Determinar los puntos de equilibrio y su estabilidad para el sistema
\[ \begin{aligned} &x^{\prime}=-2 x-3 x y \\ &y^{\prime}=3 y-y^{2} \end{aligned} \label{7.18} \]
Primero determinamos los puntos fijos. Estableciendo el lado derecho igual a cero y factorizando, tenemos
\[ \begin{aligned} -x(2+3 y) &=0 \\ y(3-y) &=0 \end{aligned} \label{7.19} \]
A partir de la segunda ecuación, vemos que cualquiera\(y=0\) o\(y=3 .\) La primera ecuación da entonces\(x=0\) en cualquiera de los casos. Entonces, hay dos puntos fijos:\((0,0)\) y\((0,3)\).
A continuación, linealizamos el sistema de ecuaciones diferenciales sobre cada punto fijo. Primero, observamos que la matriz jacobiana viene dada por
\[D \mathbf{f}(x, y)=\left(\begin{array}{cc} -2-3 y & -3 x \\ 0 & 3-2 y \end{array}\right) \nonumber \]
- Caso I Punto de equilibrio\((0,0)\).
En este caso nos encontramos con que
\[D \mathbf{f}(0,0)=\left(\begin{array}{cc} -2 & 0 \\ 0 & 3 \end{array}\right) \nonumber \]
Por lo tanto, la ecuación linealizada se convierte
\[\xi^{\prime}=\left(\begin{array}{cc} -2 & 0 \\ 0 & 3 \end{array}\right) \xi \nonumber \]
Esto se escribe equivalentemente como el sistema
\[ \begin{aligned} &\xi_{1}^{\prime}=-2 \xi_{1} \\ &\xi_{2}^{\prime}=3 \xi_{2} . \end{aligned} \label{7.23} \]
Este es el sistema linealizado sobre el origen. Anote la similitud con el sistema original. Debemos enfatizar que las ecuaciones linealizadas son ecuaciones de coeficiente constante y podemos usar métodos de matriz para determinar la naturaleza del punto de equilibrio. Los valores propios de este sistema son obviamente\(\lambda=-2,3\). Por lo tanto, tenemos que el origen es un punto de silla de montar.
- Caso II Punto de equilibrio\((0,3)\).
Nuevamente evaluamos la matriz jacobiana en el punto de equilibrio y observamos sus valores propios para determinar el tipo de punto fijo. La matriz jacobiana para este caso se convierte
\[D \mathbf{f}(0,3)=\left(\begin{array}{cc} -11 & 0 \\ 0 & -3 \end{array}\right) \nonumber \]
Los valores propios son\(\lambda=-11,-3 .\) Entonces, este punto fijo es un nodo estable.
Este análisis nos ha dado una silla de montar y un nodo estable. Sabemos cómo es el comportamiento cerca de cada punto fijo, pero tenemos que recurrir a otros medios para decir algo sobre el comportamiento lejos de estos puntos. El retrato de fase para este sistema se da en la Figura\(\PageIndex{3}\). Deberías poder ubicar el punto de sillín y el nodo en la figura. Observe cómo se comportan las soluciones en regiones alejadas de estos puntos.
Podemos esperar poder realizar una linealización bajo condiciones generales. Estos se dan en el Teorema de Hartman-Grofman:
Existe un mapa continuo entre los sistemas lineales y no lineales cuando\(D \mathbf{f}\left(\mathbf{x}^{*}\right)\) no tiene ningún valor propio con parte real cero.
Generalmente, hay varios tipos de comportamiento que se pueden ver en sistemas no lineales. Se pueden ver sumideros o fuentes, puntos hiperbólicos (sillín), puntos elípticos (centros) o focos. Hemos definido algunos de estos para sistemas planos. En general, si al menos dos valores propios tienen partes reales con signos opuestos, entonces el punto fijo es un punto hiperbólico. Si la parte real de un valor propio distinto de cero es cero, entonces tenemos un centro, o punto elíptico.
Para los sistemas lineales en el plano, esta clasificación se realizó en el Capítulo 6. La matriz jacobiana evaluada en los puntos de equilibrio es simplemente la matriz de\(2 \times 2\) coeficientes que habíamos llamado\(A\).
\[J=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \text {. } \nonumber \]
Aquí estamos usando\(J=D \mathbf{f}\left(\mathbf{x}^{*}\right)\).
La ecuación del valor propio viene dada por
\[\lambda^{2}-(a+d) \lambda+(a d-b c)=0 \nonumber \]
Sin embargo,\(a+d\) es el rastro,\(\operatorname{tr}(J)\) y\(\operatorname{det}(J)=a d-b c\). Por lo tanto, podemos escribir la ecuación del valor propio como
\[\lambda^{2}-\operatorname{tr}(J) \lambda+\operatorname{det}(J)=0 \nonumber \]
La solución de esta ecuación se encuentra utilizando la fórmula cuadrática,
\[\lambda=\dfrac{1}{2}\left[-\operatorname{tr}(J) \pm \sqrt{\operatorname{tr}^{2}(J)-4 \operatorname{det}(J)}\right]\nonumber \]
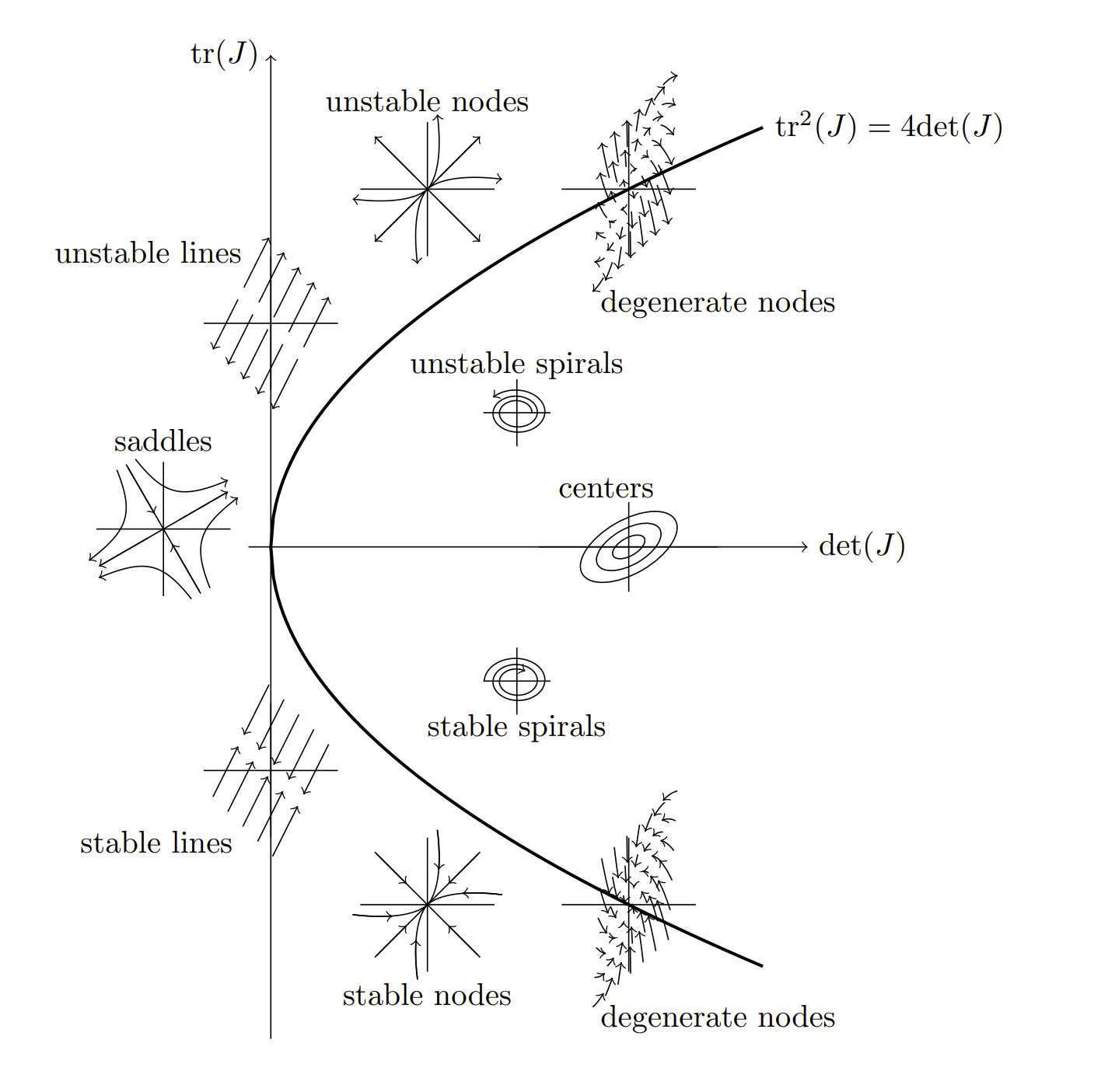
Habíamos visto en el capítulo anterior que los puntos de equilibrio en los sistemas planos pueden clasificarse como nodos, sillas de montar, centros o espirales (focos). El tipo de comportamiento se puede determinar a partir de soluciones de la ecuación de valor propio. Dado que la naturaleza de los valores propios depende de la traza y determinante de la matriz jacobiana en el punto de equilibrio, podemos relacionar los tipos de equilibrios con puntos en el plano det-tr. Esto se muestra en la Figura\(\PageIndex{4}\), que es similar a la Figura 6.7.1.
En\(\PageIndex{4}\) la Figura la parábola\(\operatorname{tr}^{2}(J)=4 \operatorname{det}(J)\) divide el plano det-tr. Los puntos en esta curva dan un discriminante de fuga en el cálculo de los valores propios. En estos casos se encuentran raíces repetidas, o valores propios. A lo largo de esta curva se pueden encontrar nodos degenerados estables e inestables. También a lo largo de esta línea se encuentran nodos propios estables e inestables, llamados nodos estrella. Éstas surgen de sistemas de la forma\(x^{\prime}=a x, y^{\prime}=a y\).
En el caso de que\(\operatorname{det}(J)<0\), tenemos que el discriminante
\[\Delta \equiv \operatorname{tr}^{2}(J)-4 \operatorname{det}(J)\nonumber \]
es positivo. No sólo eso,\(\Delta>\operatorname{tr}^{2}(J)\). Así, obtenemos dos valores propios reales y distintos con signos opuestos. Estos llevan a los puntos de sillín.
En el caso de que\(\operatorname{det}(J)>0\), podemos tener cualquiera\(\Delta>0\) o\(\Delta<0 .\) El discriminante es negativo para los puntos dentro de la curva parabólica. Es en esta región donde se encuentran centros y espirales, correspondientes a valores propios complejos. Cuando\(\operatorname{tr}(J)>0\), hay espirales inestables. Hay espirales estables cuando\(\operatorname{tr}(J)<0\). Para el caso de que\(\operatorname{tr}(J)=0\), los valores propios son puros imaginarios, dando centros.
Hay varios otros tipos de comportamiento representados en la figura, pero ahora pasaremos a estudiar algunos ejemplos.
\[\operatorname{tr}^{2}(J)=4 \operatorname{det}(J) \nonumber \]
indica dónde se desvanece el discriminante.
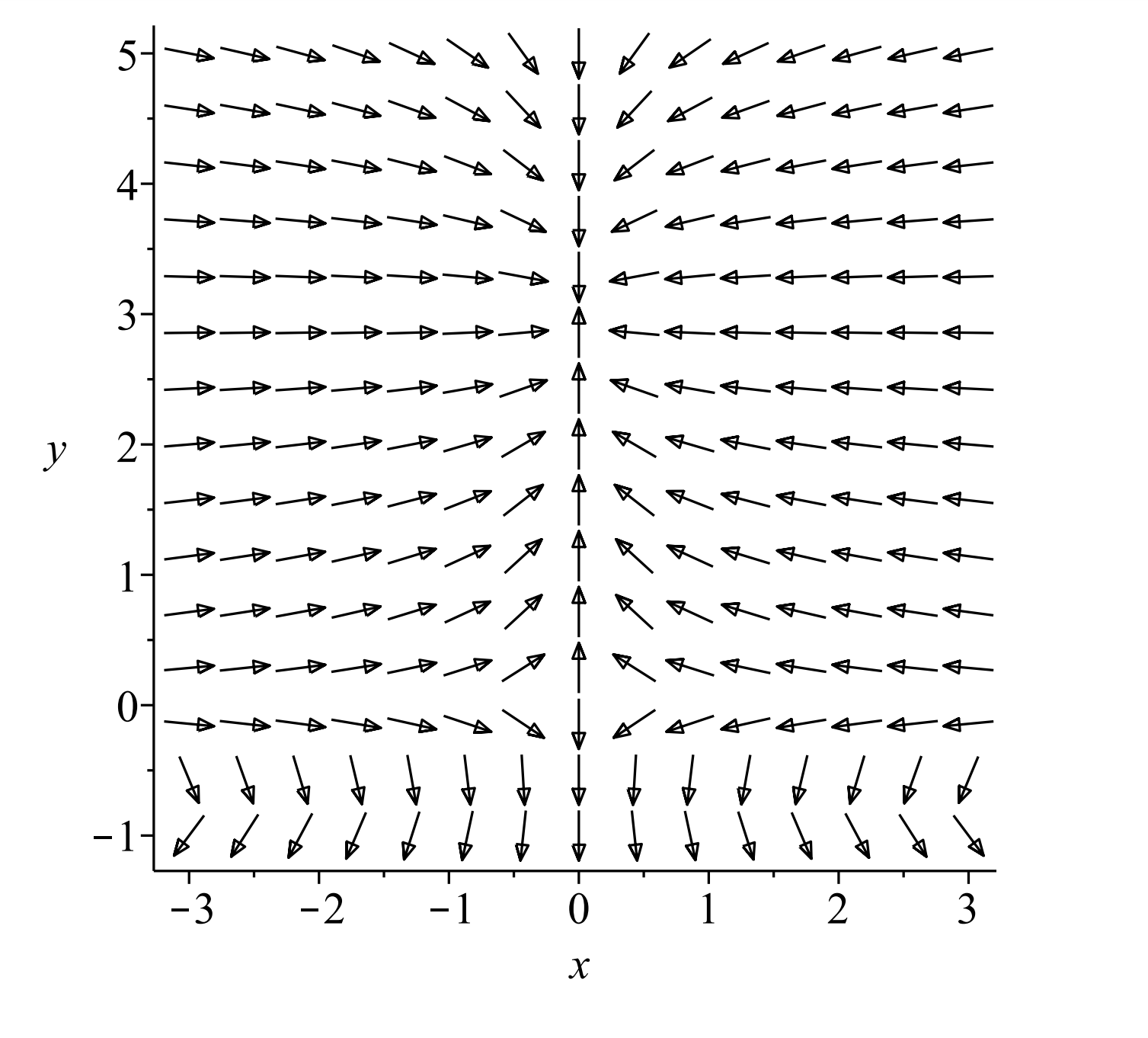
Encontrar y clasificar todas las soluciones de equilibrio del sistema no lineal.
\[ \begin{aligned} &x^{\prime}=2 x-y+2 x y+3\left(x^{2}-y^{2}\right) \\ &y^{\prime}=x-3 y+x y-3\left(x^{2}-y^{2}\right) \end{aligned}\label{7.26} \]
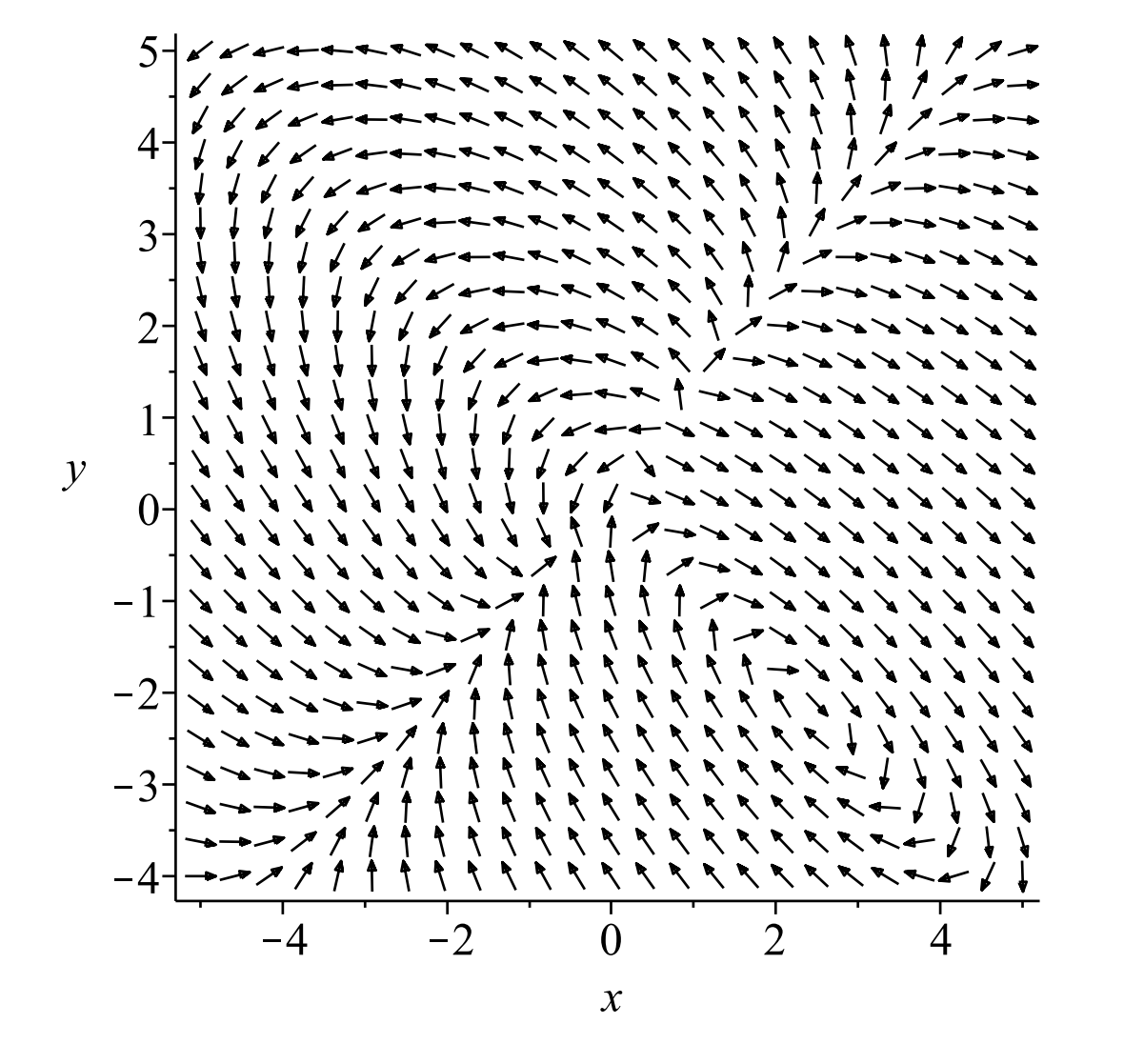
En la Figura\(\PageIndex{5}\) se muestra el campo de dirección para este sistema. Trate de localizar y clasificar visualmente los puntos de equilibrio. Después del análisis de estabilidad, debe regresar a esta cifra y determinar si identificó correctamente los puntos de equilibrio.
Primero determinaremos los puntos de equilibrio. Estableciendo el lado derecho de cada ecuación diferencial en cero, tenemos
\[ \begin{aligned} 2 x-y+2 x y+3\left(x^{2}-y^{2}\right) &=0 \\ x-3 y+x y-3\left(x^{2}-y^{2}\right) &=0 \end{aligned} \label{7.27} \]
Este sistema de ecuaciones algebraicas se puede resolver exactamente. Sumando las ecuaciones, tenemos
\[3 x-4 y+3 x y=0 \nonumber \]
\[\begin{aligned} &x^{\prime}=2 x-y+2 x y+3\left(x^{2}-y^{2}\right), \\ &y^{\prime}=x-3 y+x y-3\left(x^{2}-y^{2}\right) . \end{aligned} \nonumber \]
Resolviendo para\(x\),
\[x=\dfrac{4 y}{3(1+y)} \nonumber \]
y sustituyendo el resultado\(x\) en la primera ecuación algebraica, encontramos una ecuación para\(y\):
\[\dfrac{y(1-y)\left(9 y^{2}+22 y+5\right)}{3(1+y)^{2}}=0.\nonumber \]
Las soluciones a esta ecuación son
\[y=0,1,-\dfrac{11}{9} \pm \dfrac{2}{9} \sqrt{19}\nonumber \]
Los valores correspondientes para\(x\) son
\[x=0, \dfrac{2}{3}, 1 \mp \dfrac{\sqrt{19}}{3}.\nonumber \]
Ahora que hemos localizado los equilibrios, podemos clasificarlos. La matriz jacobiana viene dada por
\[D \mathbf{f}(x, y)=\left(\begin{array}{cc} 6 x+2 y+2 & 2 x-6 y-1 \\ -6 x+y+1 & x+6 y-3 \end{array}\right) \nonumber \]
Ahora, evaluamos el jacobiano en cada punto de equilibrio y encontramos los valores propios.
- Caso I. Punto de equilibrio\((0,0)\).
En este caso nos encontramos con que
\[D \mathbf{f}(0,0)=\left(\begin{array}{cc} -2 & -1 \\ 1 & -3 \end{array}\right) \nonumber \]
Los valores propios de esta matriz son\(\lambda=-\dfrac{1}{2} \pm \dfrac{\sqrt{21}}{2} .\) Por lo tanto, el origen es un punto de sillín.
- Caso II. Punto de equilibrio\(\left(\dfrac{2}{3}, 1\right)\).
Nuevamente evaluamos la matriz jacobiana en el punto de equilibrio y observamos sus valores propios para determinar el tipo de punto fijo. La matriz jacobiana para este caso se convierte
\[D f\left(\dfrac{2}{3}, 1\right)=\left(\begin{array}{cc} 8 & -\dfrac{17}{3} \\ -2 & \dfrac{11}{3} \end{array}\right) \nonumber \]
Los valores propios son\(\lambda=\dfrac{35}{6} \pm \dfrac{\sqrt{577}}{6} \approx 9.84,1.83 .\) Este punto fijo es un nodo inestable.
- Caso III. Punto de equilibrio\(\left(1 \mp \dfrac{\sqrt{19}}{3},-\dfrac{11}{9} \pm \dfrac{2}{9} \sqrt{19}\right)\).
La matriz jacobiana para este caso se convierte
\[D f\left(1 \mp \dfrac{\sqrt{19}}{3},-\dfrac{11}{9} \pm \dfrac{2}{9} \sqrt{19}\right)=\left(\begin{array}{cc} \dfrac{50}{9} \mp \dfrac{14}{9} \sqrt{19} & \dfrac{25}{3} \mp 2 \sqrt{19} \\ -\dfrac{56}{9} \pm \dfrac{20}{9} \sqrt{19} & -\dfrac{28}{3} \pm \sqrt{19} \end{array}\right) \nonumber \]
Hay dos puntos de equilibrio bajo este caso. El primero viene dado por
\[\left(1-\dfrac{\sqrt{19}}{3},-\dfrac{11}{9}+\dfrac{2}{9} \sqrt{19}\right) \approx(0.453,-0.254)\nonumber \]
Los valores propios para este punto son
\[\lambda=-\dfrac{17}{9}-\dfrac{5}{18} \sqrt{19} \pm \dfrac{1}{18} \sqrt{3868 \sqrt{19}-16153}\nonumber \]
Estos son aproximadamente\(-4.58\) y\(-1.62\) Así, este punto de equilibrio es un nodo estable.
El otro equilibrio es\(\left(1+\dfrac{\sqrt{19}}{3},-\dfrac{11}{9}-\dfrac{2}{9} \sqrt{19}\right) \approx(2.45,-2.19) .\) Los valores propios correspondientes son complejos con partes reales negativas,
\[\lambda=-\dfrac{17}{9}+\dfrac{5}{18} \sqrt{19} \pm \dfrac{i}{18} \sqrt{16153+3868 \sqrt{19}}\nonumber \]
o\(\lambda \approx-0.678 \pm 10.1 i\). Este punto es una espiral estable.
Las gráficas del plano de fase se dan en las Figuras\(\PageIndex{3}\) y\(\PageIndex{5}\). El lector puede mirar el campo de dirección y verificar estos resultados para el comportamiento de las soluciones de equilibrio. En la Figura se muestra una vista ampliada\(\PageIndex{6}\) con varias órbitas indicadas.
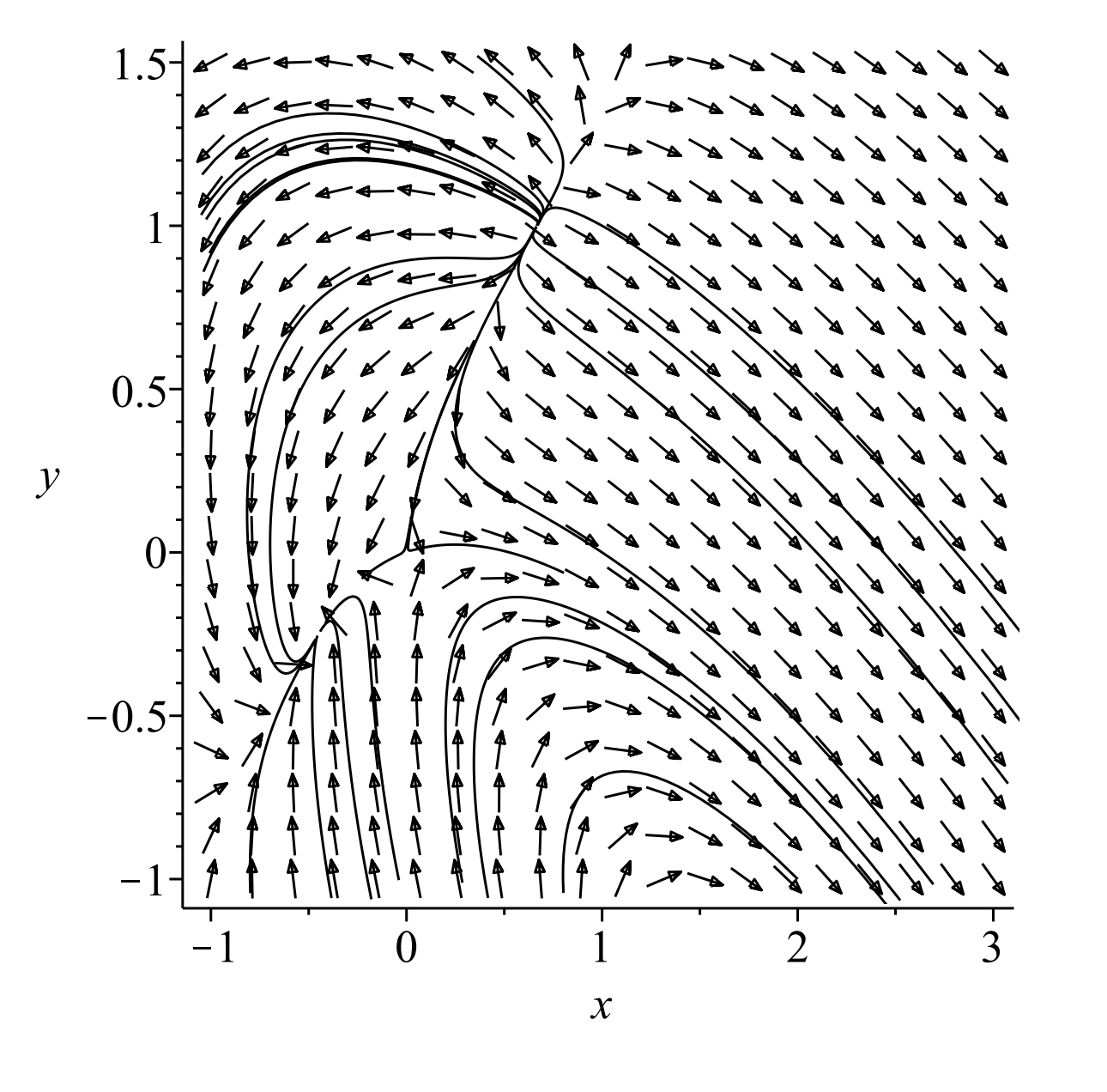
\[\begin{gathered} x^{\prime}=2 x-y+2 x y+3\left(x^{2}-y^{2}\right) \\ y^{\prime}=x-3 y+x y-3\left(x^{2}-y^{2}\right) \end{gathered}\nonumber \]
con algunas trayectorias mostradas.
Ahora estamos listos para establecer el comportamiento de los puntos fijos del sistema de péndulo no lineal amortiguado en la Ecuación\(\PageIndex{4}\). Recordemos que el sistema para el péndulo no lineal amortiguado fue dado por
\[ \begin{aligned} x^{\prime} &=y \\ y^{\prime} &=-b y-\omega^{2} \sin x \end{aligned} \label{7.32} \]
Para un sistema amortiguado, necesitaremos\(b>0\). Habíamos encontrado que hay un número infinito de puntos de equilibrio en\((n \pi, 0), n=0, \pm 1, \pm 2, \ldots\)
La matriz jacobiana para este sistema es
\[ D \mathbf{f}(x, y)=\left(\begin{array}{cc} 0 & 1 \\ -\omega^{2} \cos x & -b \end{array}\right) \nonumber \]
Evaluando esta matriz en los puntos fijos, encontramos que
\[D \mathbf{f}(n \pi, 0)=\left(\begin{array}{cc}0 & 1 \\ -\omega^{2} \cos n \pi & -b\end{array}\right)=\left(\begin{array}{cc}0 & 1 \\ (-1)^{n+1} \omega^{2} & -b\end{array}\right) \nonumber \]
La ecuación del valor propio viene dada por
\[\lambda^{2}+b \lambda+(-1)^{n} \omega^{2}=0 \nonumber \]
Hay dos casos a considerar:\(n\) par\(n\) e impar. Para el primer caso, encontramos los valores propios
\[\lambda=\dfrac{-b \pm \sqrt{b^{2}-4 \omega^{2}}}{2} \nonumber \]
Porque\(b^{2}<4 \omega^{2}\), tenemos dos raíces conjugadas complejas con una parte real negativa. Así, tenemos focos estables para\(n\) valores pares. Si no hay amortiguación, entonces obtenemos centros\((\lambda=\pm i \omega)\).
En el segundo caso,\(n\) impar, encontramos
\[\lambda=\dfrac{-b \pm \sqrt{b^{2}+4 \omega^{2}}}{2} \nonumber \]
Ya que\(b^{2}+4 \omega^{2}>b^{2}\), estas raíces serán reales con signos opuestos. Así, tenemos puntos hiperbólicos, o sillas de montar. Si no hay amortiguación, los valores propios se reducen a\(\lambda=\pm \omega\).
En la Figura\(\PageIndex{7}\) se muestra el plano de fase para el péndulo no lineal no amortiguado con\(\omega=1.25\). Vemos que tenemos una mezcla de centros y sillas de montar. Hay órbitas para las que hay movimiento periódico. En el caso de que\(\theta = \pi\) tengamos un péndulo invertido. Esta es una posición inestable y esto se refleja en la presencia de puntos de sillín, especialmente si el péndulo se construye utilizando una varilla sin masa.
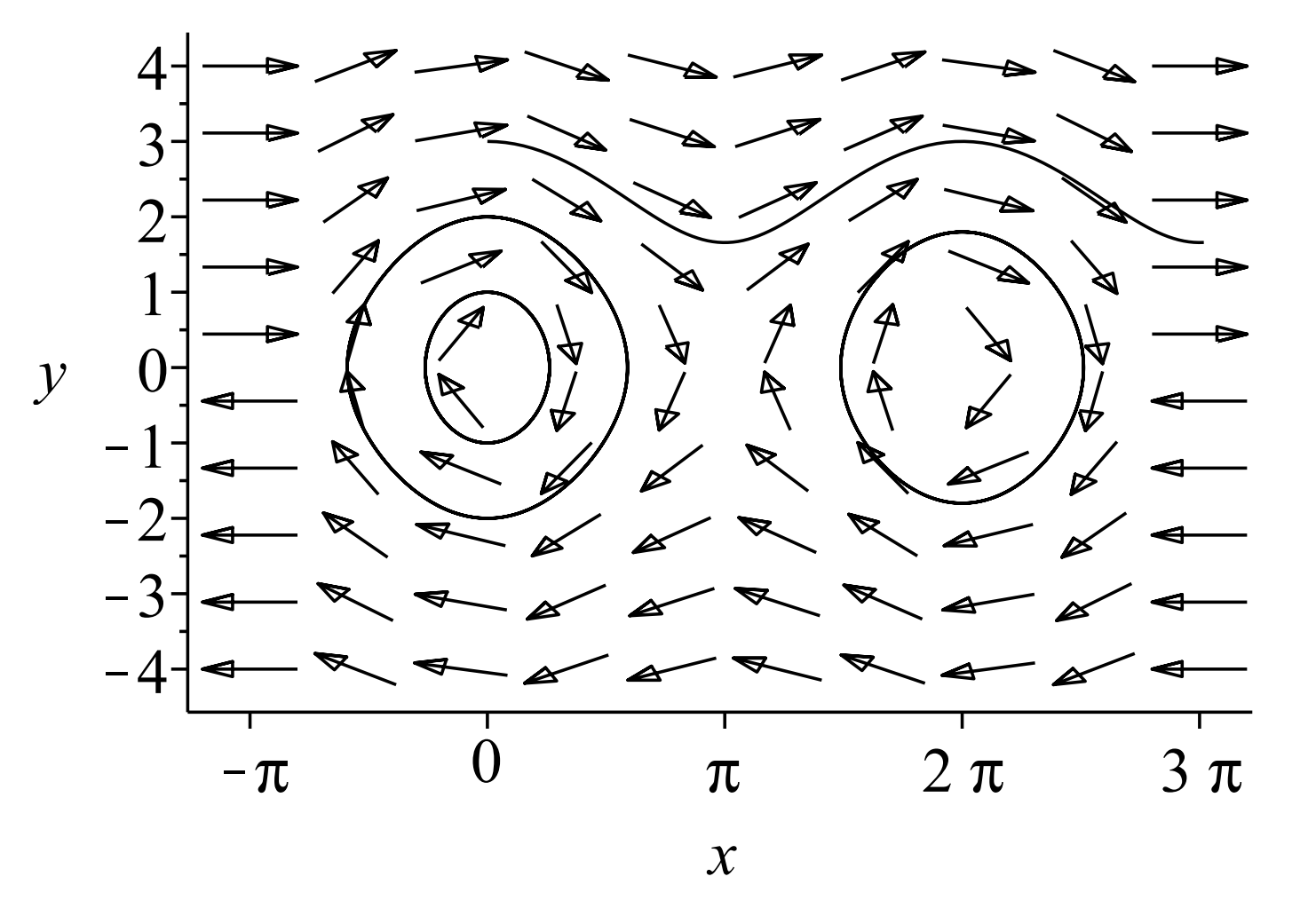
También hay órbitas sin límites, pasando por todos los ángulos posibles. Estos corresponden a la masa girando alrededor del pivote en una dirección para siempre debido a tener inicialmente energías suficientemente grandes.
Hemos indicado en la figura curvas de solución con las condiciones iniciales\(\left(x_{0}, y_{0}\right)=(0,3),(0,2),(0,1),(5,1)\). Estos muestran los diversos tipos de movimientos que hemos descrito.
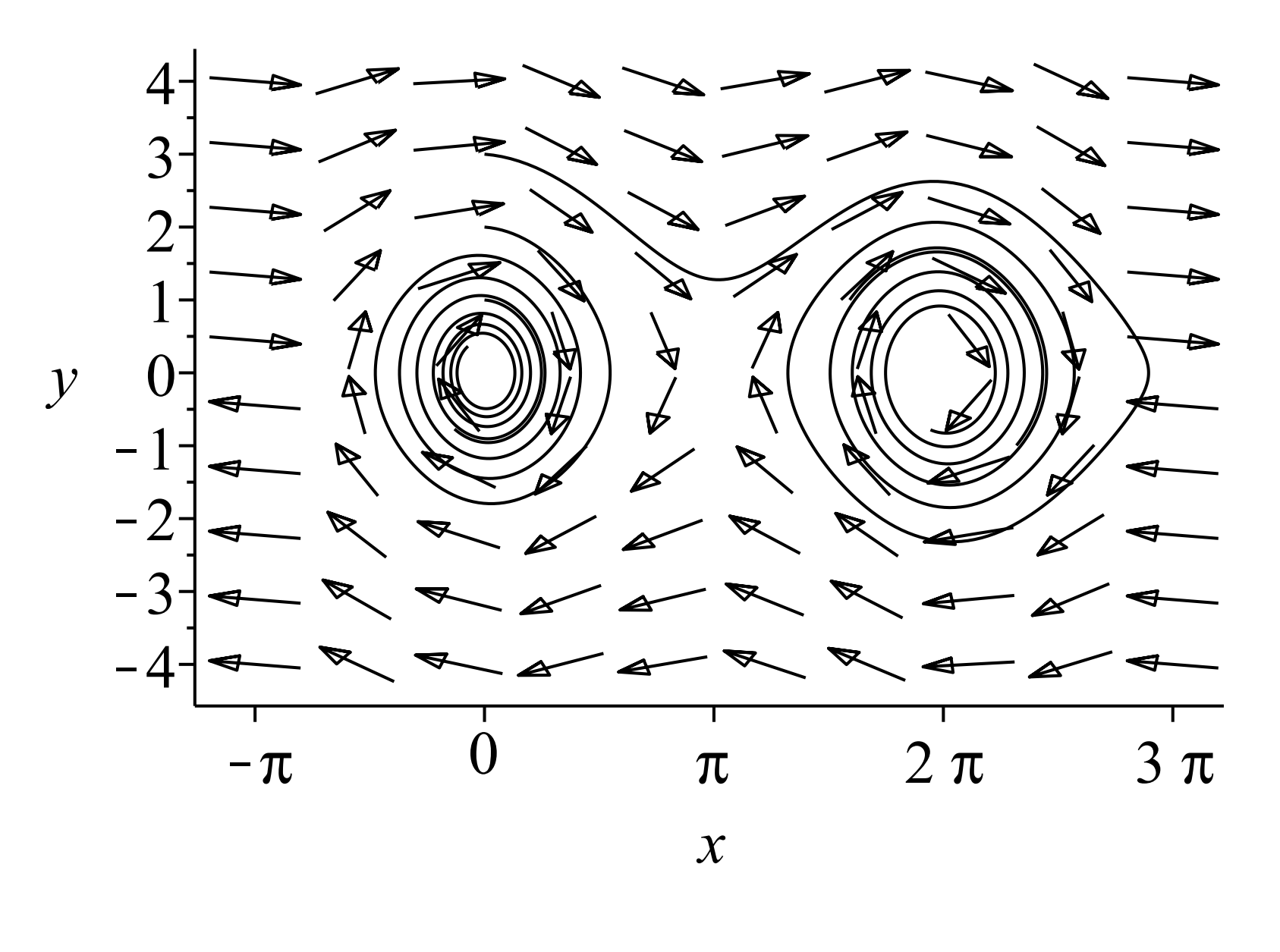
Cuando hay amortiguación, vemos que podemos tener una variedad de otros comportamientos como se ve en la Figura\(\PageIndex{8}\). En este ejemplo hemos establecido\(b=0.08\) y\(\omega=1.25 .\) vemos que la pérdida de energía da como resultado que la masa se asiente alrededor de uno de los puntos fijos estables. Esto lleva a comprender por qué hay un número infinito de equilibrios, a pesar de que físicamente la masa traza un conjunto atado de puntos cartesianos. Hemos indicado en la Figura curvas de\(\PageIndex{8}\) solución con las condiciones iniciales\(\left(x_{0}, y_{0}\right)=(0,3),(0,2),(0,1),(5,1)\).
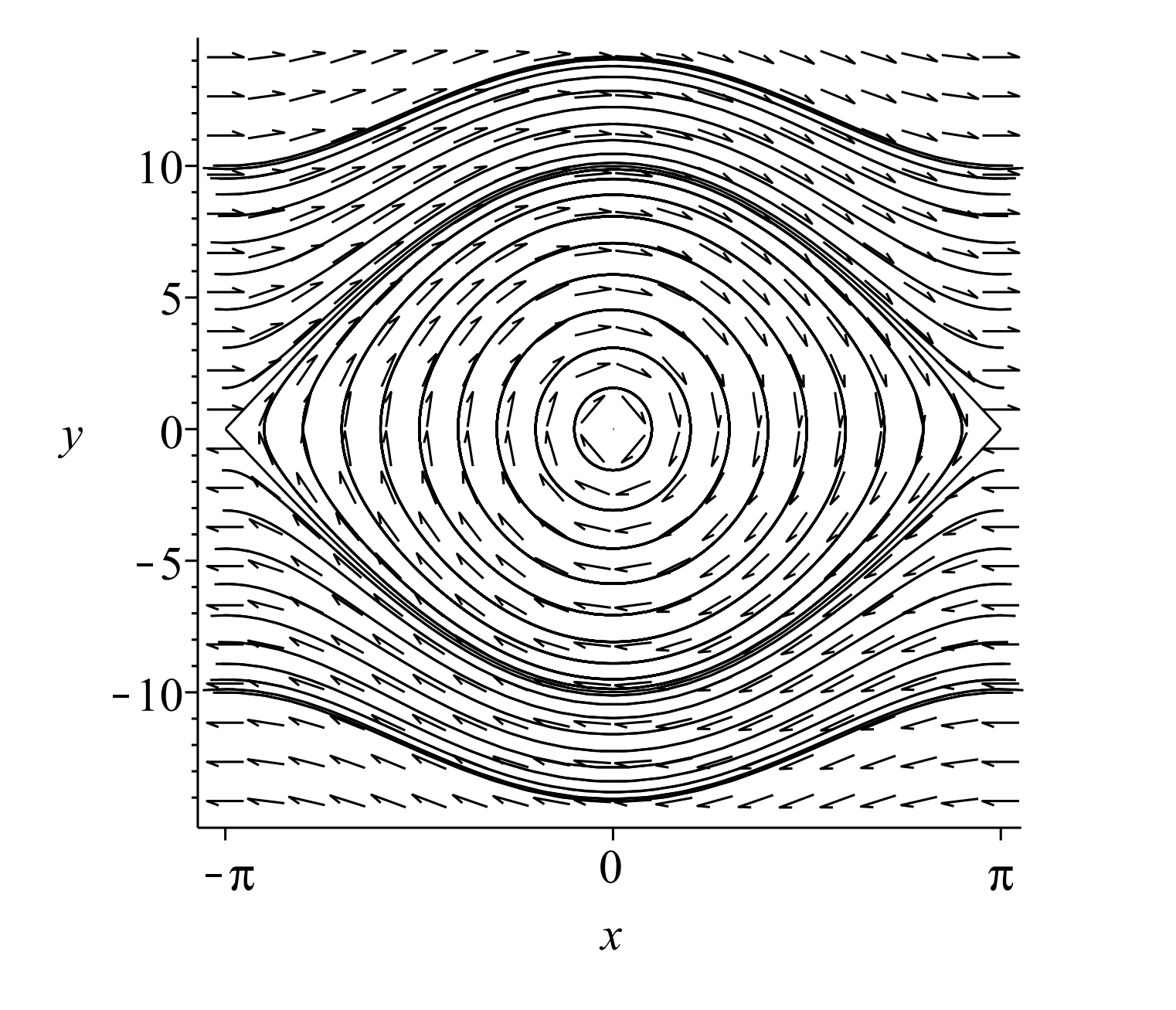
En la Figura\(\PageIndex{9}\) se muestra una región del plano de fase que corresponde a oscilaciones alrededor\(x=0\). Para ángulos pequeños el péndulo oscila siguiendo órbitas algo elípticas. A medida que los ángulos se hacen más grandes, debido a mayores energías iniciales, estas órbitas comienzan a cambiar de elipses a otras órbitas periódicas. Hay una órbita limitante, más allá de la cual se tiene un movimiento sin límites. La órbita limitadora conecta los puntos de sillín a ambos lados del centro. La curva se llama separatriz y siendo que estas trayectorias conectan dos sillas de montar, a menudo se las conoce como órbitas heteroclínicas.
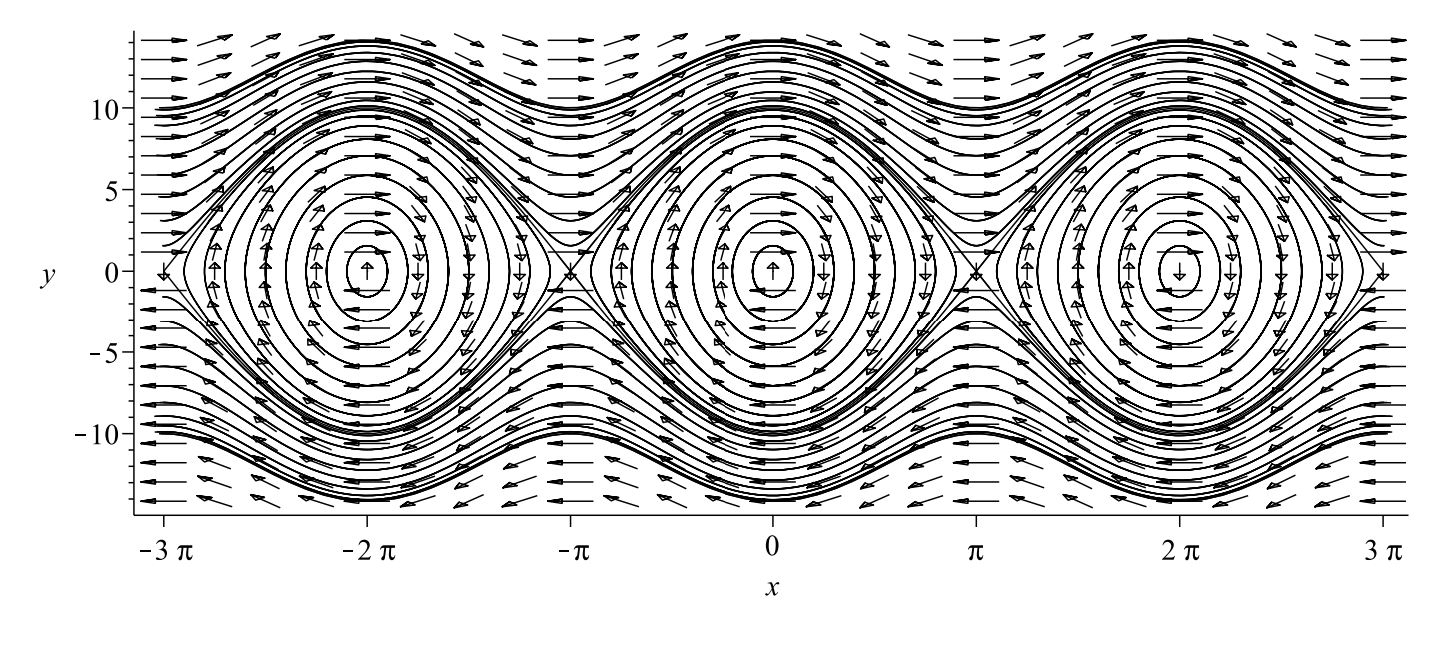
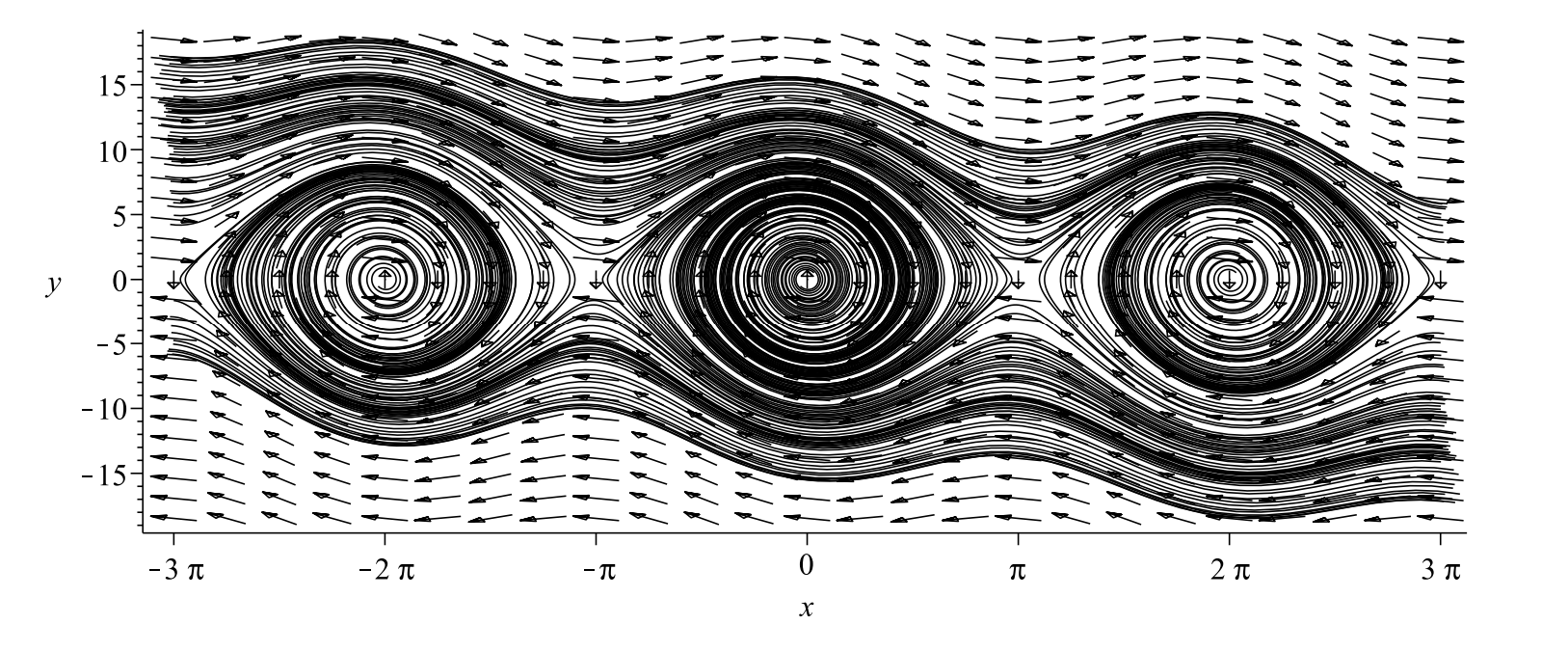
(Órbitas heteroclinas y separatrices). En las Figuras\(\PageIndex{10}\) se muestran más órbitas, incluyendo tanto el movimiento ligado como el no unido más allá del intervalo\(x \in[-\pi, \pi]\). Para ambas parcelas hemos elegido\(\omega=5\) y el mismo conjunto de condiciones iniciales,\(x(0)=\pi k / 10, k=\)\(-20, \ldots, 20\). para\(y(0)=0, \pm 10\). El intervalo de tiempo se toma para\(t \in[-3,3]\). La única diferencia es que en el caso amortiguado que tenemos\(b=0.5 .\) En estas parcelas se puede ver lo que sucede con las órbitas heteroclínicas y órbitas cercanas no acotadas bajo amortiguamiento.
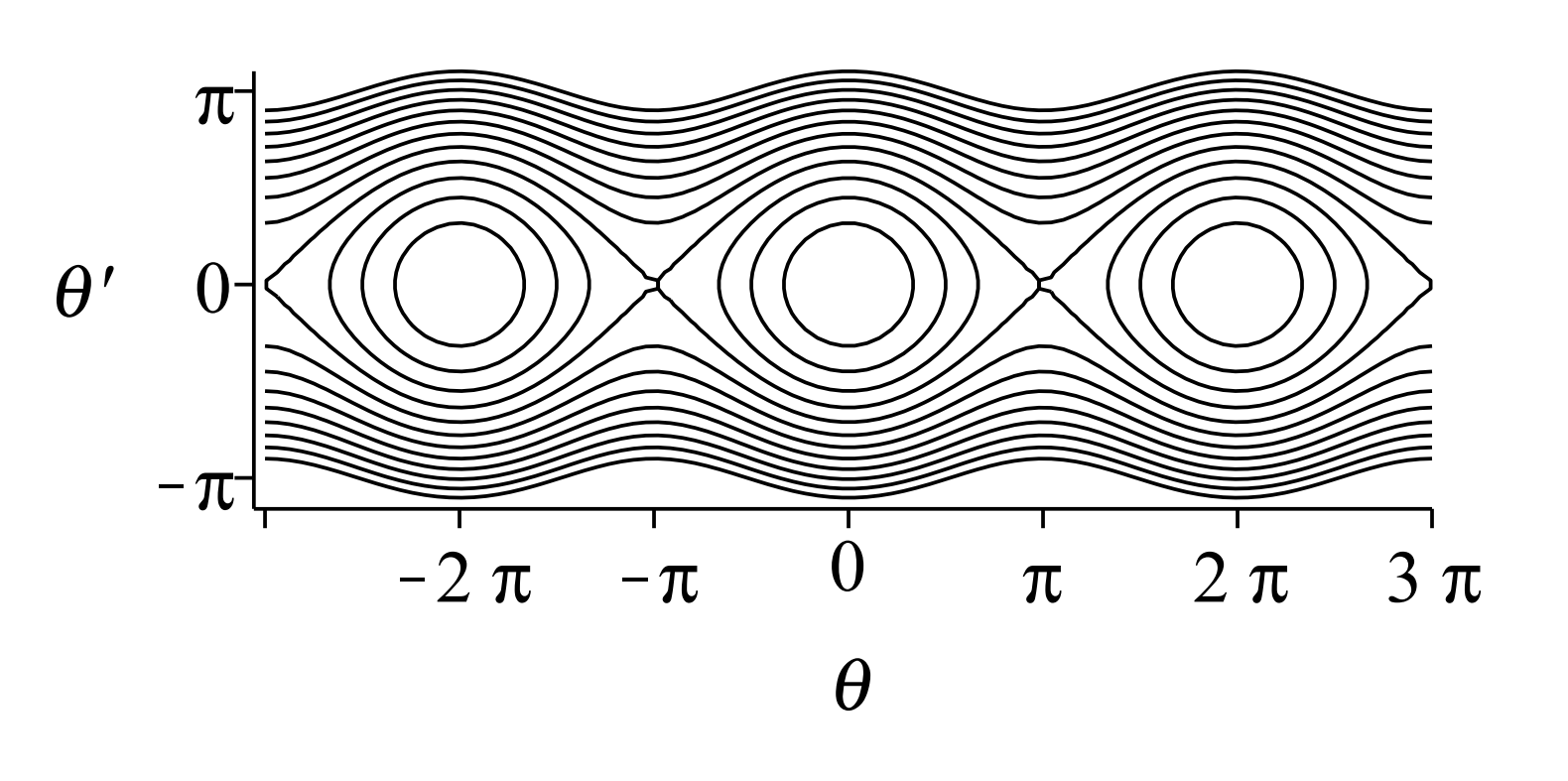
Antes de dejar este problema, debemos señalar que las órbitas en el plano de fase para el péndulo no lineal no amortiguado se pueden obtener gráficamente. Recordemos de la Ecuación 7.9.6, la energía mecánica total para el péndulo no lineal es
\[E=\dfrac{1}{2} m L^{2} \dot{\theta}^{2}+m g L(1-\cos \theta) \nonumber \]
De esta ecuación se obtuvo la Ecuación 7.9.7,
\[\dfrac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta=-\omega^{2} \cos \theta_{0} \nonumber \]
Dejar\(y=\dot{\theta}, x=\theta\), y definir\(z=-\omega^{2} \cos \theta_{0}\), esta ecuación puede escribirse como
\[\dfrac{1}{2} y^{2}-\omega^{2} \cos x=z \nonumber \]
Por cada energía\((z)\), esto da una curva de energía constante. Trazando la familia de curvas de energía obtenemos el retrato de fase que se muestra en la Figura\(\PageIndex{12}\).