7.6: Modelos de Población No Lineales
- Page ID
- 119658
YA NOS HEMOS ENCONTRADO VARIOS MODELOS DE DINÁMICA DE POBLACIÓN EN ESTE Por supuesto, uno podría soñar con varios otros ejemplos. Si bien tales modelos pueden parecer distantes de ser aplicaciones en física, resulta que estos modelos conducen a sistemas de ecuaciones diferenciales que también aparecen en sistemas físicos como el acoplamiento de ondas en láseres, en física de plasma y en reacciones químicas.
El modelo Lotka-Volterra lleva el nombre del modelo se ve similar, excepto que hay algunos cambios de signos, ya que una especie Alfred James Lotka (188o-1949) y Vito Volterra (1860-1940). no se alimenta de la otra. Además, podemos construir en términos logísticos en nuestro modelo. Vamos a guardar este último tipo de modelo para la tarea.
Dos modelos de población no lineal bien conocidos son los modelos depredador-presa y especies competidoras. En el modelo depredador-presa, una suele tener una especie, el depredador, alimentándose de la otra, la presa. Veremos el modelo estándar Lotka-Volterra en esta sección. Las especies competidoras
(El modelo Lotka-Volterra de dinámica poblacional). El modelo Lotka-Volterra toma la forma
\[ \begin{aligned} & \dot{x}=a x-b x y, \\ & \dot{y}=-d y+c x y, \end{aligned} \label{7.36} \]
donde\(a, b, c\), y\(d\) son constantes positivas. En este modelo, podemos pensar en la población de conejos (presas) y\(y\) es la población de zorros (depredadores).\(x\) Eligiendo todas las constantes para que sean positivas, podemos describir los términos.
- \(ax\): Cuando se deja sola, la población de conejos crecerá. Así\(a\) es la tasa de crecimiento natural sin depredadores.
- \(-d y\):Cuando no hay conejos, la población de zorros debe decaer. Por lo tanto, el coeficiente necesita ser negativo.
- \(-bxy\): Añadimos un término no lineal correspondiente al agotamiento de los conejos cuando los zorros están alrededor.
- \(cxy\): Cuantos más conejos haya, más comida para los zorros. Entonces, agregamos un término no lineal dando lugar a un incremento en la población de zorros.
Determinar los puntos de equilibrio y su estabilidad para el sistema Lotka-Volterra.
El análisis del modelo Lotka-Volterra comienza con la determinación de los puntos fijos. Entonces, tenemos de Ecuación\(\PageIndex{1}\)
\[ \begin{aligned} x(a-b y) &=0, \\ y(-d+c x) &=0 . \end{aligned} \label{7.37} \]
Por lo tanto, el origen\((0,0)\),, y\(\left(\dfrac{d}{c}, \dfrac{a}{b}\right)\) son los puntos fijos.
A continuación, determinamos su estabilidad, por linealización sobre los puntos fijos. Podemos usar la matriz jacobiana, o podríamos simplemente expandir el lado derecho de cada ecuación en la Ecuación\(\PageIndex{1}\) sobre los puntos de equilibrio como se muestra en el siguiente ejemplo. La matriz jacobiana para este sistema es
\[\operatorname{Df}(x, y)=\left(\begin{array}{cc} a-b y & -b x \\ c y & -d+c x \end{array}\right) \nonumber \]
Evaluando en cada punto fijo, tenemos
\[D f(0,0)=\left(\begin{array}{cc} a & 0 \\ 0 & -d \end{array}\right) , \nonumber \]
\[D f\left(\dfrac{d}{c}, \dfrac{a}{b}\right)=\left(\begin{array}{cc} 0 & -\dfrac{b d}{c} \\ \dfrac{a c}{b} & 0 \end{array}\right) . \nonumber \]
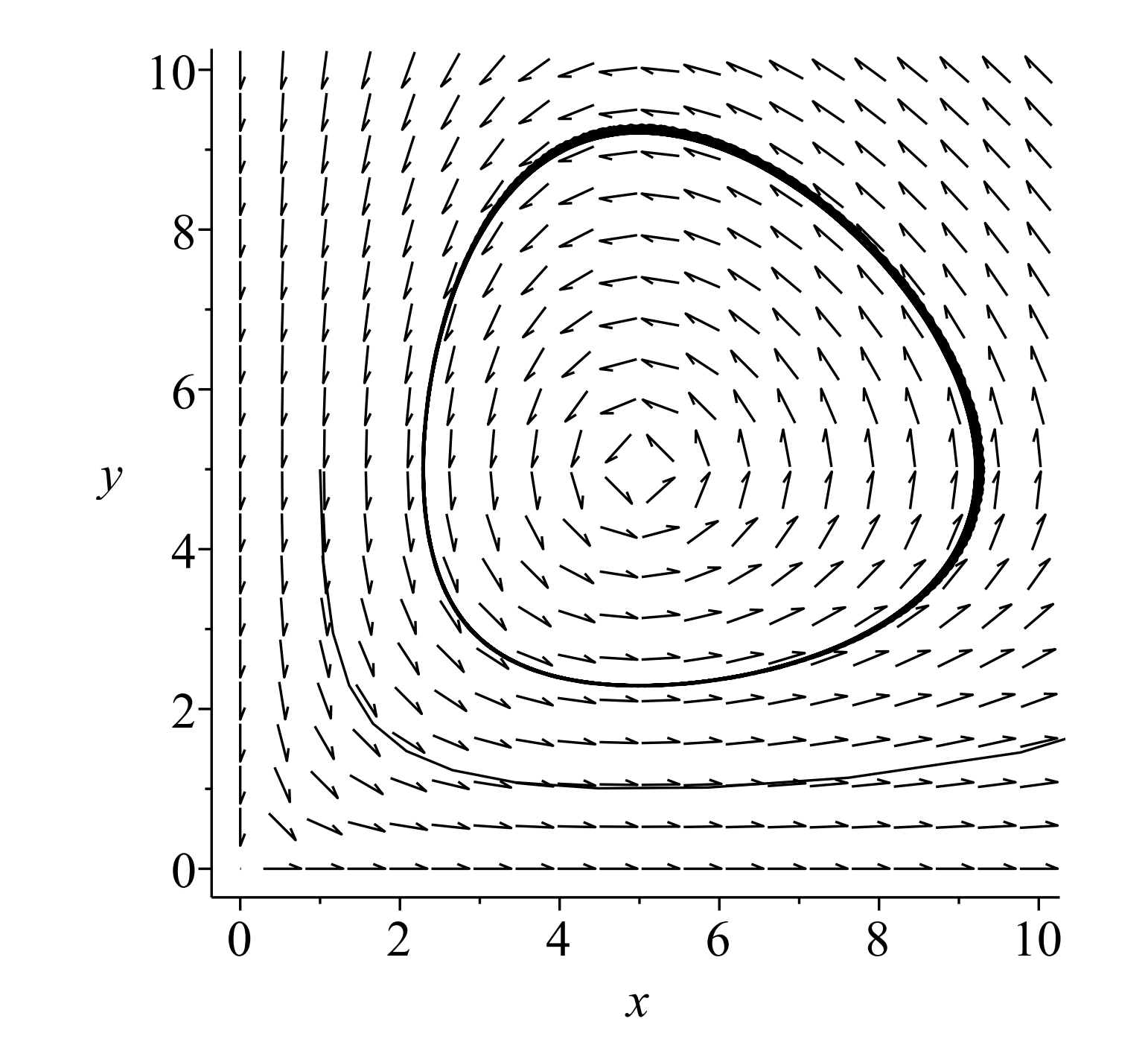
Los valores propios de\(\left(7 \cdot 3^{8}\right)\) son\(\lambda=a,-d .\) So, el origen es un punto de silla de montar.
Los valores propios de la Ecuación\(\PageIndex{4}\) satisfacen\(\lambda^{2}+a d=0 .\) Entonces, el otro punto es un centro. En la Figura\(\PageIndex{1}\) se muestra un campo de dirección de muestra para el sistema Lotka-Volterra.
Otra forma de llevar a cabo la linealización del sistema de ecuaciones diferenciales es ampliar las ecuaciones sobre los puntos fijos. Para puntos fijos\((x^{*}, y^{*})\), dejamos
\[(x, y)=\left(x^{*}+u, y^{*}+v\right) \nonumber \]
La inserción de esta traducción del origen en las ecuaciones del sistema, y la caída de términos no lineales en\(u\) y\(v\), da como resultado el sistema linealizado. Este método equivale a analizar la matriz jacobiana para cada punto fijo.
La linealización directa de un sistema se lleva a cabo introduciendo\(\mathbf{x}=\mathbf{x}^{*}+\xi\), o\((x, y)=\left(x^{*}+u, y^{*}+v\right)\) dentro del sistema y dejando caer términos no lineales en\(u\) y\(v\).
Ampliar el sistema Lotka-Volterra sobre los puntos de equilibrio.
Para el origen\((0,0)\) la linealización sobre el origen equivale a simplemente dejar caer los términos no lineales. En este caso tenemos
\ [\ begin {alineado}
&\ punto {u} =a u,\\
&\ punto {v} =-d v.
\ end {alineado}\ etiqueta {7.40}\]
La matriz de coeficientes para este sistema es la misma que\(D f(0, 0)\).
Para el segundo punto fijo, dejamos
\[(x,y)=\dfrac{d}{c}+u, \dfrac{a}{b} +v\). \nonumber \]
Insertar esta transformación en el sistema da
\ [\ begin {aligned}
\ dot {u} &=a\ left (\ frac {d} {c} +u\ right) -b\ left (\ frac {d} {c} {c} +u\ right)\ left (\ frac {a} {b} +v\ right)
\\ dot {v} &=-d\ left (\ frac {a} {b} +v\ derecha) +c\ izquierda (\ frac {d} {c} +u\ derecha)\ izquierda (\ frac {a} {b} +v\ derecha).
\ end {alineado}\ etiqueta {7.41}\]
Ampliando, obtenemos
\[ \begin{aligned} \dot{u} &=\dfrac{a d}{c}+a u-b\left(\dfrac{a d}{b c}+\dfrac{d}{c} v+\dfrac{a}{b} u+u v\right) \\ \dot{v} &=-\dfrac{a d}{b}-d v+c\left(\dfrac{a d}{b c}+\dfrac{d}{c} v+\dfrac{a}{b} u+u v\right) \end{aligned} \label{7.42} \]
En ambas ecuaciones los términos constantes cancelan y linealización es simplemente deshacerse de los\(u v\) términos. Esto deja el sistema linealizado
\[ \begin{aligned} \dot{u} &=a u-b\left(\dfrac{d}{c} v+\dfrac{a}{b} u\right) \\ \dot{v} &=-d v+c\left(+\dfrac{d}{c} v+\dfrac{a}{b} u\right) \end{aligned}\label{7.43} \]
O
\[ \begin{aligned} \dot{u} &=-\dfrac{b d}{c} v, \\ \dot{v} &=\dfrac{a c}{b} u . \end{aligned} \label{7.44} \]
La matriz de coeficientes para este sistema linealizado es la misma que\(D f\left(\dfrac{d}{c}, \dfrac{a}{b}\right)\). De hecho, para órbitas cercanas, son órbitas casi circulares. De este sistema linealizado, tenemos\(\ddot{u}+a d u=0\).
Podemos tomar\(u=A \cos (\sqrt{a d} t+\phi)\), donde\(A\) y se\(\phi\) puede determinar a partir de las condiciones iniciales. Entonces,
\[ \begin{aligned} v &=-\dfrac{c}{b d} \dot{u} \\ &=\dfrac{c}{b d} A \sqrt{a d} \sin (\sqrt{a d} t+\phi) \\ &=\dfrac{c}{b} \sqrt{\dfrac{a}{d}} A \sin (\sqrt{a d} t+\phi) \end{aligned} \label{7.45} \]
Por lo tanto, las soluciones cercanas al centro son dadas por
\[(x, y)=\left(\dfrac{d}{c}+A \cos (\sqrt{a d} t+\phi), \dfrac{a}{b}+\dfrac{c}{b} \sqrt{\dfrac{a}{d}} A \sin (\sqrt{a d} t+\phi)\right). \nonumber \]
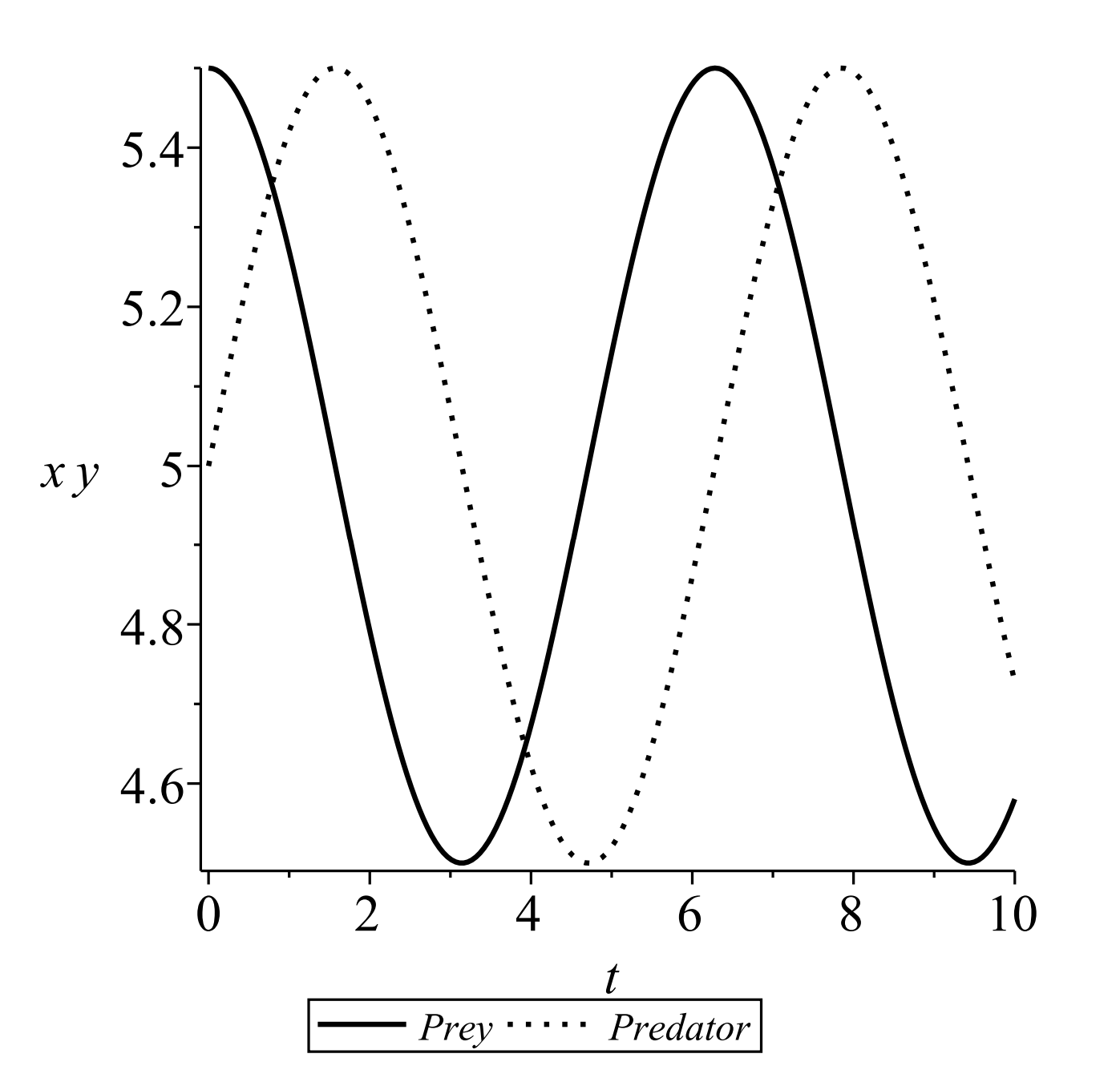
Para\(a=d=1, b=c=0.2\), y los valores iniciales de\(\left(x_{0}, y_{0}\right)=(5.5,5)\), estas soluciones se convierten
\[x(t)=5.0+0.5 \cos t, \quad y(t)=5.0+0.5 \sin t\nonumber \]
Las gráficas de estas soluciones se muestran en la Figura\(\PageIndex{2}\).
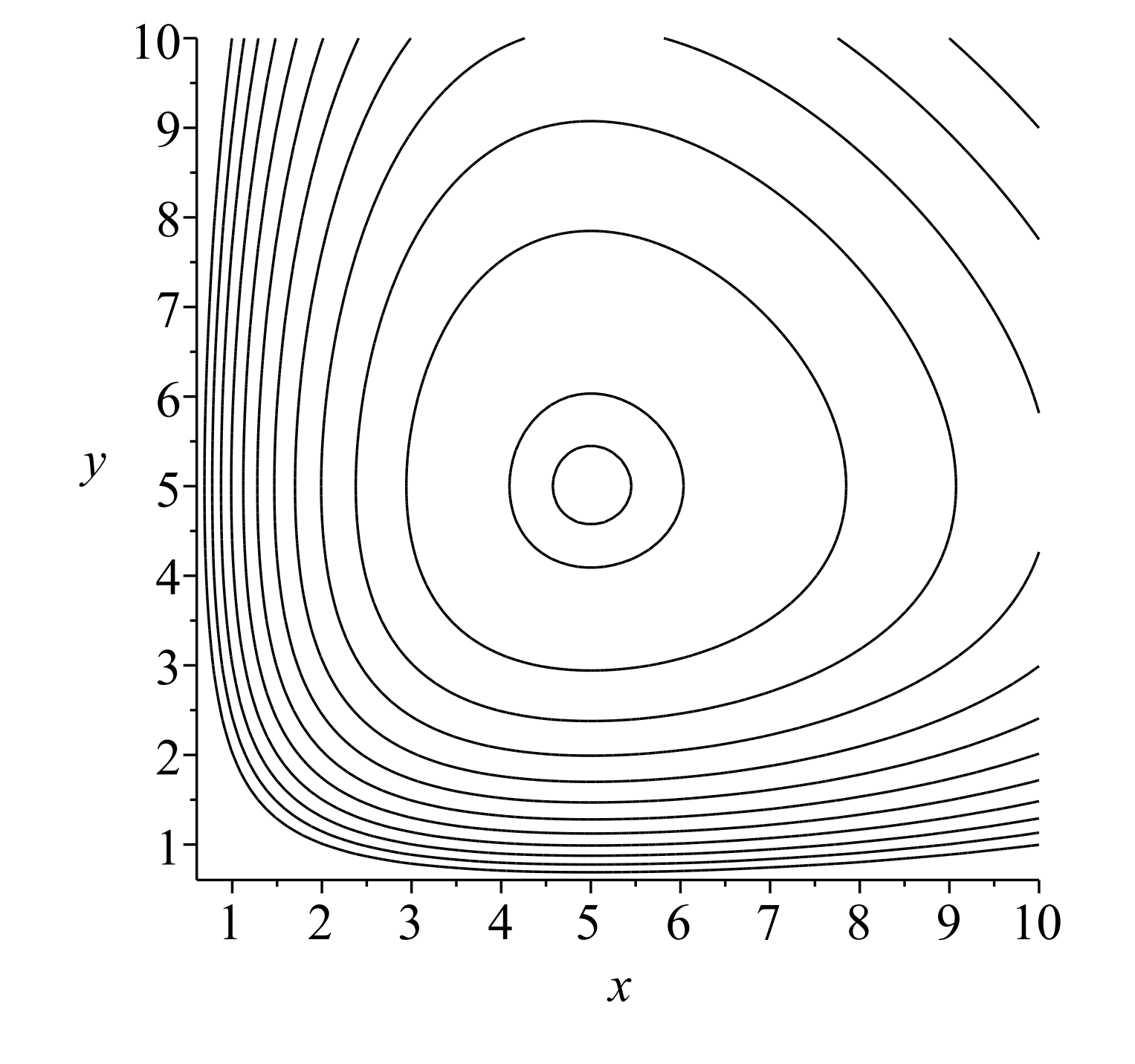
También es posible encontrar una primera integral del sistema Lotka-Volterra cuyas curvas de nivel dan el retrato de fase del sistema. Como habíamos hecho en el Capítulo 2, podemos escribir
\[\begin{aligned} \dfrac{d y}{d x} &=\dfrac{\dot{y}}{\dot{x}} \\ &=\dfrac{-d y+c x y}{a x-b x y} \\ &=\dfrac{y(-d+c x)}{x(a-b y)} \end{aligned} \label{7.46} \]
Esta es una ecuación de la forma vista en el Problema 2.6.13. Esta ecuación es ahora una ecuación diferencial separable. La solución de esta ecuación diferencial se da en forma implícita como
\[a ln y + d ln x − cx − by = C \nonumber \]
,
donde\(C\) es una constante arbitraria. Esta expresión se conoce como el primer sistema.