7.4: Bifurcaciones para Ecuaciones de Primer Orden

Ahora consideramos familias de ecuaciones diferenciales autónomas de primer orden de la forma

\[\dfrac{d y}{d t}=f(y ; \mu) \nonumber \]

Aquí\(\mu\) hay un parámetro que podemos cambiar y luego observar los comportamientos resultantes de las soluciones de la ecuación diferencial. Cuando un pequeño cambio en el parámetro conduce a cambios en el comportamiento de la solución, entonces se dice que el sistema se somete a una bifurcación. El valor del parámetro,\(\mu\), en el que se produce la bifurcación se denomina punto de bifurcación.

Consideraremos varios ejemplos genéricos, dando lugar a clases especiales de bifurcaciones de ecuaciones diferenciales autónomas de primer orden. Estudiaremos la estabilidad de las soluciones de equilibrio utilizando ambas líneas de fase y los criterios de estabilidad desarrollados en la última sección

Ejemplo\(\PageIndex{1}\)

\(y^{\prime}=y^{2}-\mu\).

Solución

Primero señalar que las soluciones de equilibrio ocurren para\(y^{2}=\mu .\) En este problema, hay tres casos a considerar.

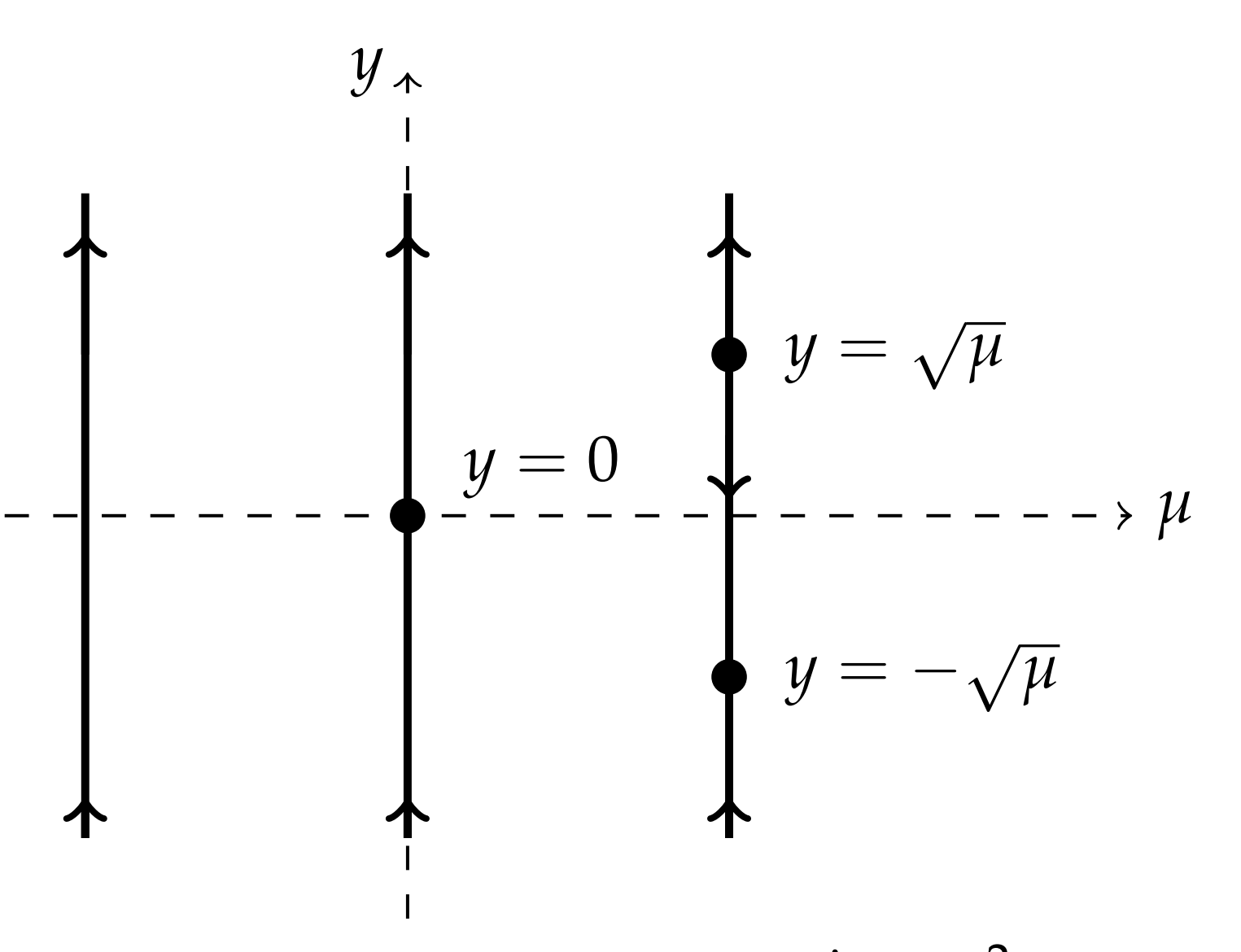
1. \(\mu>0\).

En este caso hay dos soluciones reales de\(y^{2}=\mu, y=\pm \sqrt{\mu}\). Tenga en cuenta que\(y^{2}-\mu<0\) para\(|y|<\sqrt{\mu}\). Entonces, tenemos la línea de fase correcta en la Figura\(\PageIndex{1}\)\).

Figura\(\PageIndex{1}\): Líneas de fase para\(y^{\prime}=y^{2}-\mu\) .A la derecha\(\mu>0\) y a la izquierda\(\mu<0\).

2. \( \mu = 0\).

Solo hay un punto de equilibrio en\(y=0\). La ecuación se vuelve\(y^{\prime}=y^{2} .\) Es obvio que el lado derecho de esta ecuación nunca es negativo. Entonces, la línea de fase, que se muestra como la línea media en la Figura\(\PageIndex{1}\), tiene flechas que apuntan hacia arriba.

3. \(\mu<0\).

En este caso no hay soluciones de equilibrio. Ya que\(y^{2}-\mu>0\), las pendientes para todas las soluciones son positivas como lo indica la última línea de fase en la Figura\(\PageIndex{1}\).

También podemos confirmar los comportamientos de los puntos de equilibrio señalando que\(f^{\prime}(y)=2 y .\) Entonces,\(f^{\prime}(\pm \sqrt{\mu})=\pm 2 \sqrt{\mu}\) para\(\mu \geq 0 .\) Por lo tanto, los equilibrios\(y=+\sqrt{\mu}\) son equilibrios inestables para\(\mu>0 .\) Similarmente, los equilibrios\(y=-\sqrt{\mu}\) son equilibrios estables para\(\mu>0\).

Podemos combinar estos resultados para las líneas de fase en un diagrama conocido como diagrama de bifurcación. Trazaremos las soluciones de equilibrio y sus líneas de fase\(y=\pm \sqrt{\mu}\) en el\(\mu y\) plano. Comenzamos alineando las líneas de fase para varios\(\mu^{\prime}\) s. Estas se muestran en el lado izquierdo de la Figura\(7.6\). Tenga en cuenta que el patrón de puntos de equilibrio se encuentra en la curva parabólica\(y^{2}=\mu\). La rama superior de esta curva es una colección de equilibrios inestables y la parte inferior es una rama estable. Entonces, podemos disponer de las líneas de fase y simplemente mantener los equilibrios. Sin embargo, dibujaremos la rama inestable como una línea discontinua y la rama estable como una línea continua.

Figura\(\PageIndex{2}\): (a) Las líneas de fase típicas para\(y' = y^2 − \mu\). (b) Diagrama de bifurcación para\(y' = y^2 − \mu\). Este es un ejemplo de una bifurcación de nodo de silla de montar.

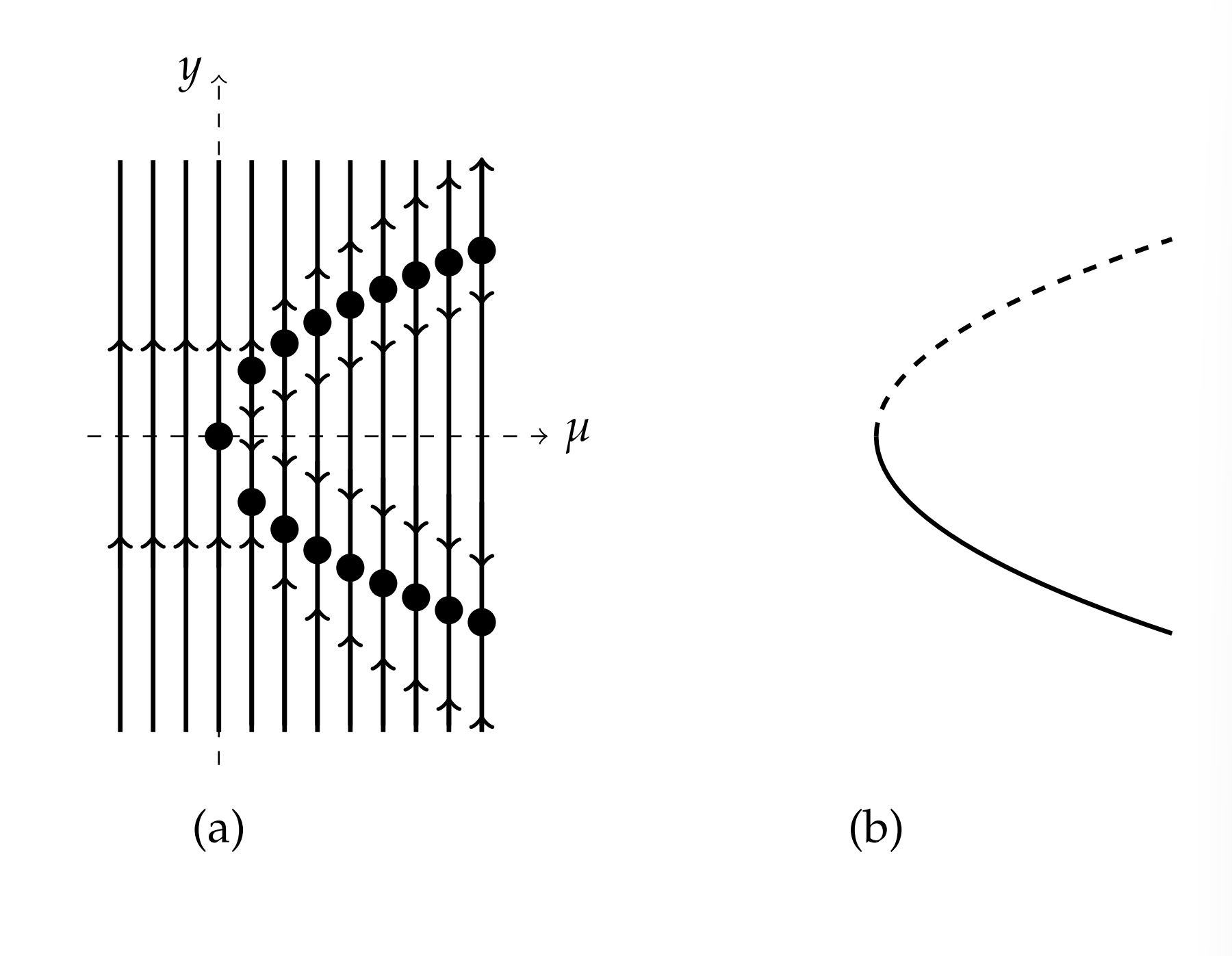
El diagrama de bifurcación se muestra en el lado derecho de la Figura\(\PageIndex{2}\). Este tipo de bifurcación se denomina bifurcación de nodo de silla de montar. El punto\(\mu=0\) en el que cambia el comportamiento es el punto de bifurcación. A medida que\(\mu\) cambia de valores negativos a positivos, el sistema pasa de no tener equilibrios a tener un punto de equilibrio estable y otro inestable.

Ejemplo\(\PageIndex{2}\)

\(y^{\prime}=y^{2}-\mu y\).

Solución

Escribiendo esta ecuación en forma factorizada\(y^{\prime}=y(y-\mu)\),, vemos que hay dos puntos de equilibrio,\(y=0\) y\(y=\mu\). El comportamiento de las soluciones depende del signo de\(y^{\prime}=y(y-\mu)\). Esto lleva a cuatro casos con los signos indicados de la derivada. Las regiones que indican los signos de\(y^{\prime}\) se muestran en la Figura\(7 \cdot 7\).

1. \(y>0, y-\mu>0 \Rightarrow y^{\prime}>0\).
2. \(y<0, y-\mu>0 \Rightarrow y^{\prime}<0\).
3. \(y>0, y-\mu<0 \Rightarrow y^{\prime}<0\).
4. \(y<0, y-\mu<0 \Rightarrow y^{\prime}>0\).

Figura\(\PageIndex{3}\): Las regiones que indican los diferentes signos de la derivada para\(y^{\prime}=\)\(y^{2}-\mu y\).

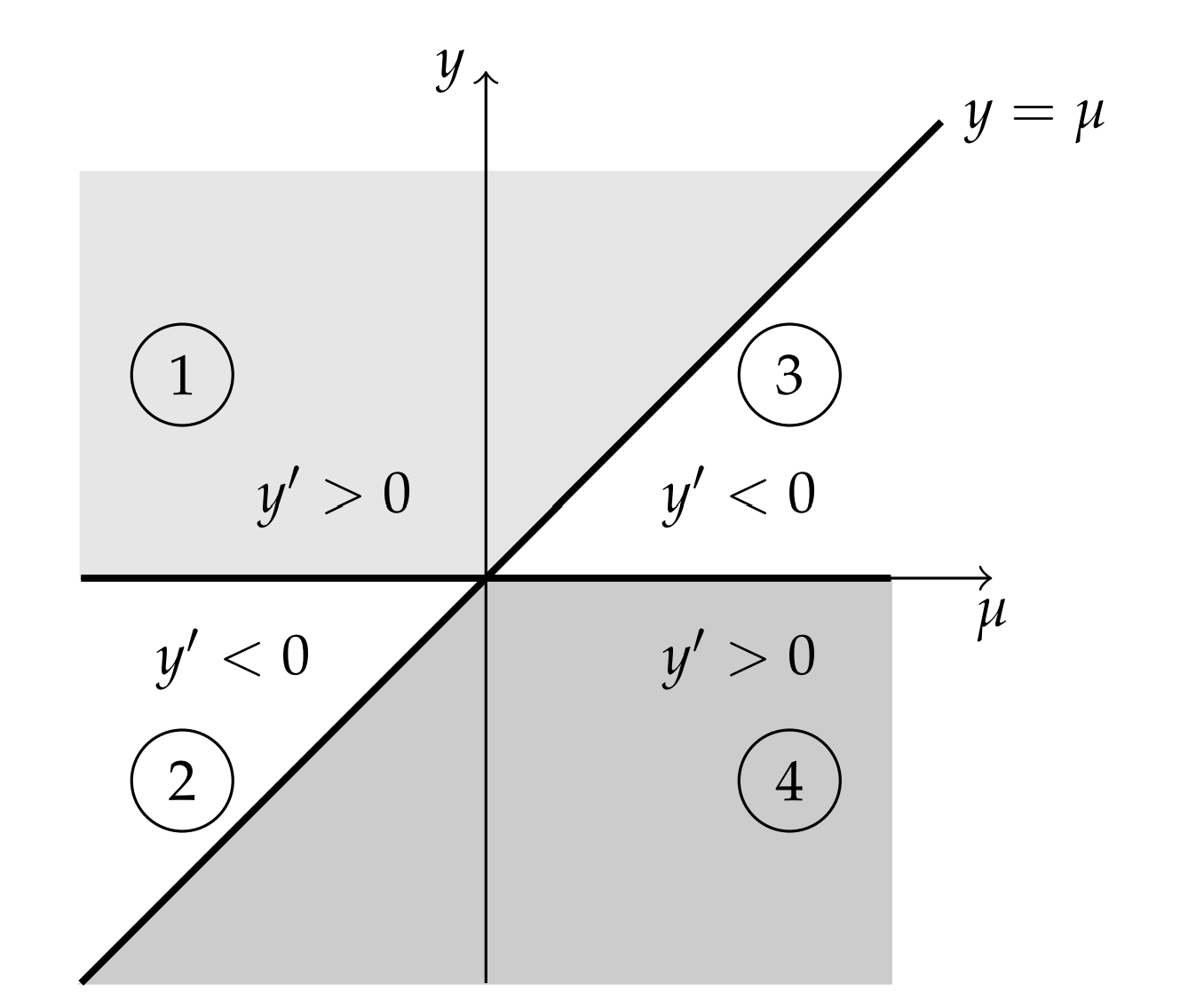
En la figura se muestran las líneas de fase correspondientes y el diagrama de bifurcación superpuesta\(7.8\). El diagrama de bifurcación se encuentra en el lado derecho de la Figura\(7.8\) y este tipo de bifurcación se denomina bifurcación transcrítica.

De nuevo, la estabilidad se puede determinar a partir de la derivada\(f^{\prime}(y)=\)\(2 y-\mu\) evaluada en\(y=0, \mu\). De\(f^{\prime}(0)=-\mu\), vemos que\(y=0\) es estable para\(\mu>0\) e inestable para\(\mu<0\). De igual manera,\(f^{\prime}(\mu)=\mu\) implica que\(y=\mu\) es inestable para\(\mu>0\) y estable para\(\mu<0 .\) Estos resultados son consistentes con las gráficas de línea de fase.

Ejemplo\(\PageIndex{3}\)

\(y^{\prime}=y^{3}-\mu y\).

Solución

Para este último ejemplo, encontramos a partir de\(y^{3}-\mu y=y\left(y^{2}-\mu\right)=0\) eso hay dos casos.

1. \(\mu<0 .\)En este caso solo hay un punto de equilibrio en\(y=0 .\) Para valores positivos de\(y\) tenemos eso\(y^{\prime}>0\) y para valores negativos de\(y\) tenemos eso\(y^{\prime}<0\). Por lo tanto, este es un punto de equilibrio inestable.

Figura\(\PageIndex{4}\): (a) Recogida de líneas de fase para\(y^{\prime}=y^{2}-\mu y\). (b) Diagrama de bifurcación para\(y^{\prime}=y^{2}-\mu y\). Este es un ejemplo de bifurcación transcrítica.

Figura\(\PageIndex{5}\): (a) Las líneas de fase para\(y^{\prime}=\)\(y^{3}-\mu y\). El izquierdo corresponde a\(\mu<\) 0 y la línea de fase derecha es para\(\mu>0\). (b) Diagrama de bifurcación para\(y^{\prime}=y^{3}-\mu y\). Este es un ejemplo de bifurcación de horca.

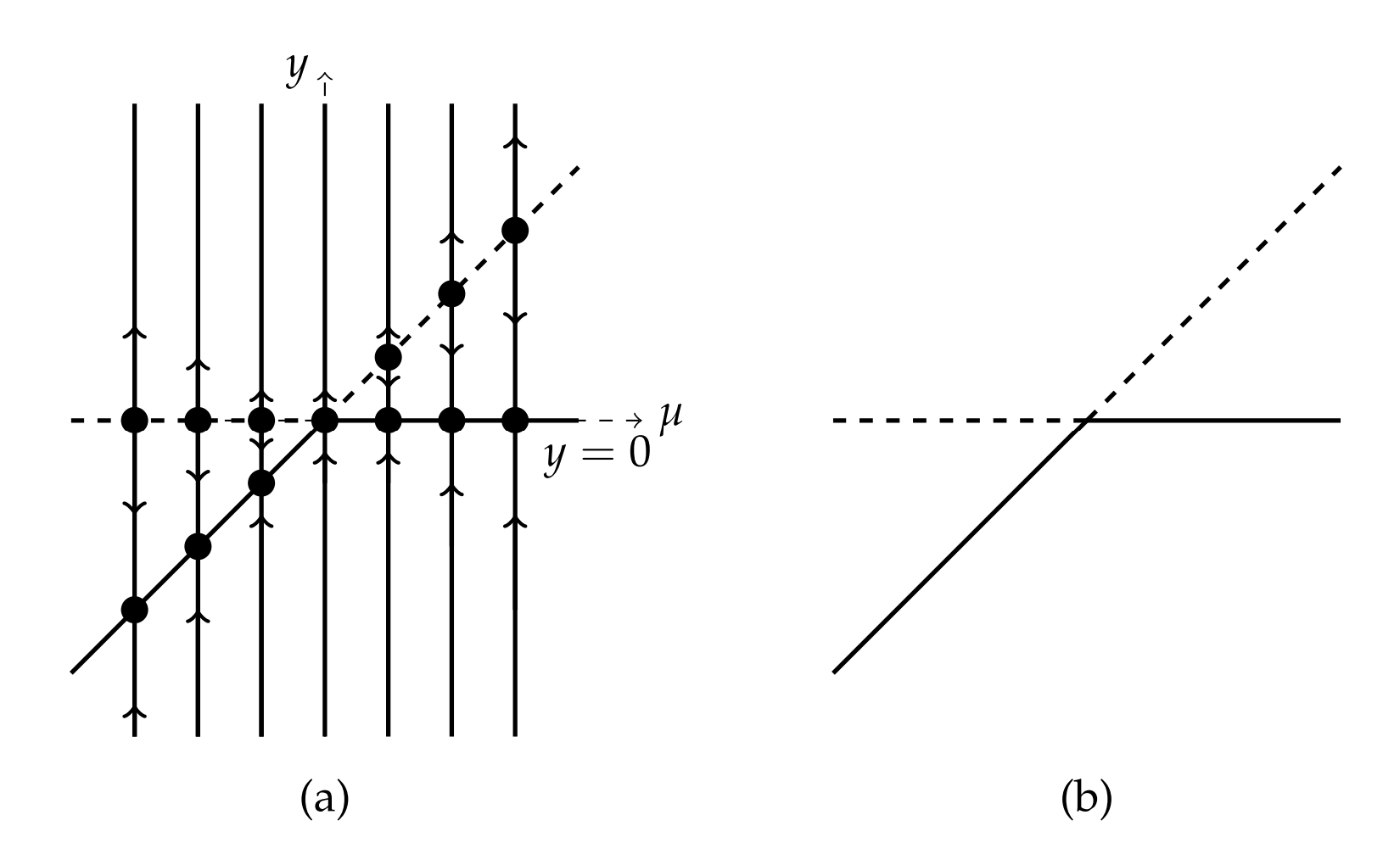
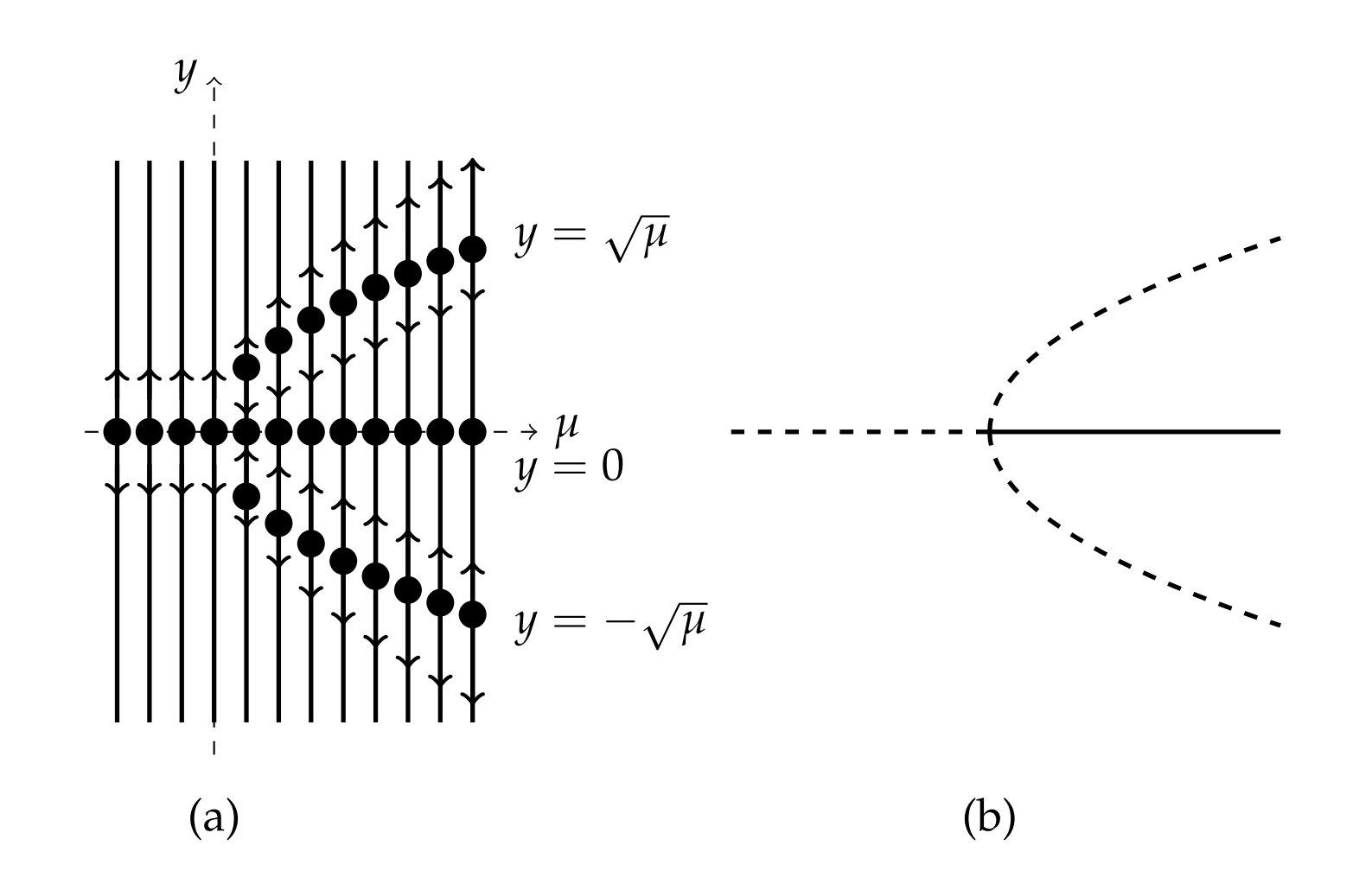
Cuando dos de las puntas de la horca son ramas inestables, la bifurcación se llama bifurcación de horca subcrítica. Cuando dos dientes son ramas estables, la bifurcación es una bifurcación de horca supercrítica.

2. \(\mu>0 .\)Aquí tenemos tres equilibrios,\(y=0, \pm \sqrt{\mu} .\) Una investigación cuidadosa muestra que\(y=0\) es un punto de equilibrio estable y que los otros dos equilibrios son inestables.

En la Figura\(\PageIndex{5}\)\) se muestran las líneas de fase para estos dos casos. Luego se esboza el diagrama de bifurcación correspondiente en el lado derecho de la Figura\(\PageIndex{5}\). Por razones obvias esto ha sido etiquetado como una bifurcación de horca.

Ya que\(f^{\prime}(y)=3 y^{2}-\mu\), el análisis de estabilidad da\(f^{\prime}(0)=-\mu .\) que So,\(y=0\) es estable para\(\mu>0\) e inestable\(\mu<0 .\) para\(\mu>0\) For, tenemos eso\(f^{\prime}(\pm \sqrt{\mu})=2 \mu\). Por lo tanto\(y=\pm \sqrt{\mu}, \mu>0\),, es inestable. Así, tenemos una bifurcación subcrítica de horca.