7.7: Límite de ciclos
- Page ID
- 119675
Hasta el momento nos acaban de preocupar las soluciones de equilibrio y su comportamiento. Sin embargo, los puntos fijos asintóticamente estables no son los únicos atractores. Existen otros tipos de soluciones, conocidas como ciclos límite, hacia los que puede tender una solución. En esta sección veremos algunos ejemplos de estas soluciones periódicas.
Tales soluciones son de naturaleza común. Rayleigh investigó el problema
\[x^{\prime \prime}+c\left(\dfrac{1}{3}\left(x^{\prime}\right)^{2}-1\right) x^{\prime}+x=0 \nonumber \]
en el estudio de las vibraciones de una cuerda de violín. Balthasar van der Pol (1889-1959) estudió un circuito eléctrico, modelando este comportamiento. Otros han investigado sistemas biológicos, como los sistemas neuronales, las reacciones químicas, como la cinética de Michaelis-Menten y otros sistemas químicos que conducen a oscilaciones químicas. Uno de los modelos más importantes en el estudio histórico de los sistemas dinámicos es el del movimiento planetario y la investigación de la estabilidad de las órbitas planetarias. Como es bien sabido, estas órbitas son periódicas.
Los ciclos límite son soluciones periódicas aisladas hacia las que los estados vecinos pueden tender cuando son estables. Un ejemplo clave que exhibe un ciclo límite se da en el siguiente ejemplo.
Encuentra el ciclo límite en el sistema
\[ \begin{aligned} x^{\prime} &=\mu x-y-x\left(x^{2}+y^{2}\right) \\ y^{\prime} &=x+\mu y-y\left(x^{2}+y^{2}\right) \end{aligned} \label{7.48} \]
Solución
Es claro que el origen es un punto fijo. La matriz jacobiana se da como
\[D f(0,0)=\left(\begin{array}{cc} \mu & -1 \\ 1 & \mu \end{array}\right) \nonumber \]
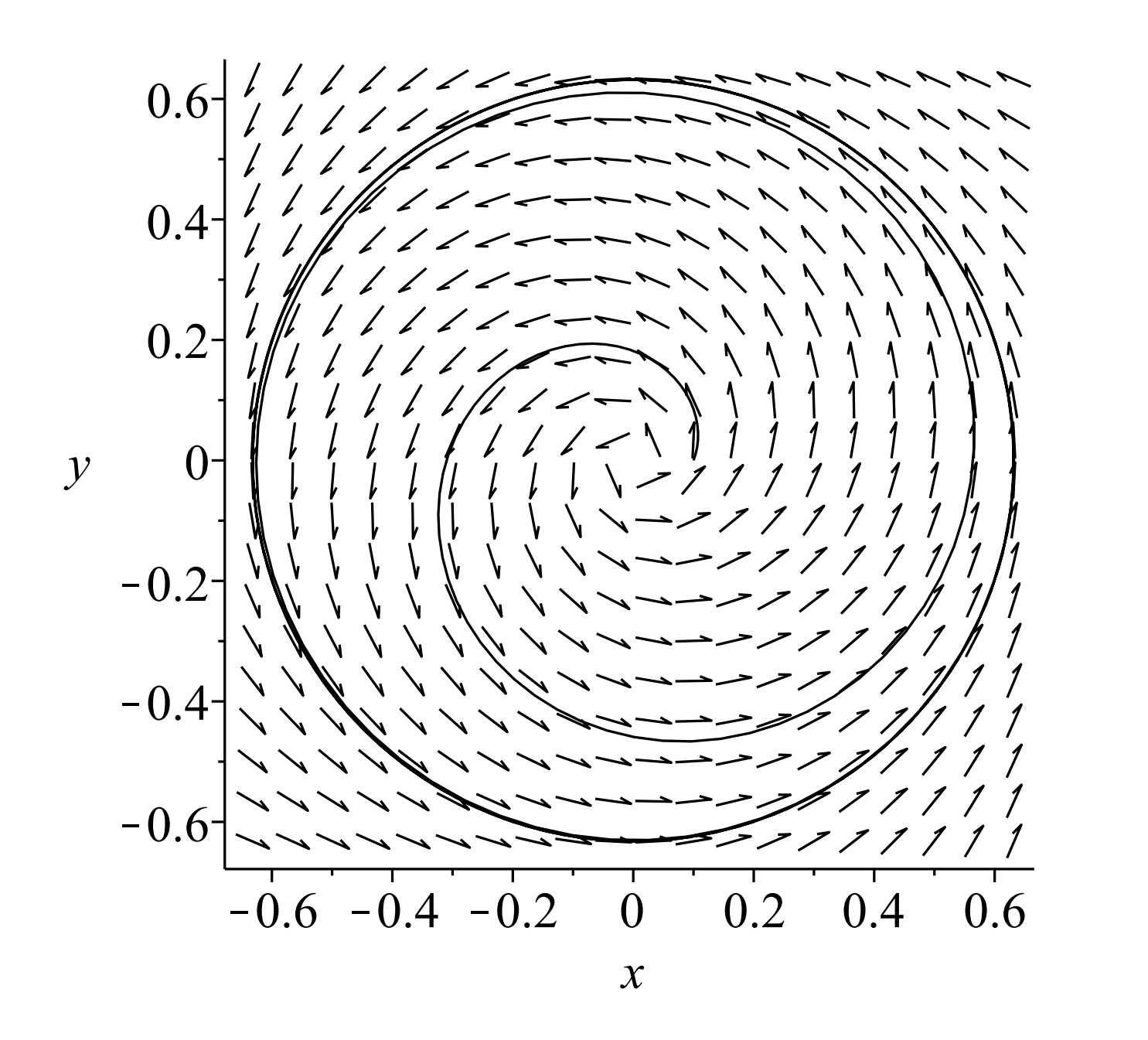
Se encuentra que los valores propios son\(\lambda=\mu \pm i\). Porque\(\mu=0\) tenemos un centro. Porque\(\mu<0\) tenemos una espiral estable y para\(\mu>0\) tenemos una espiral inestable. Sin embargo, esta espiral no vaga hacia el infinito. Vemos en la Figura\(\PageIndex{1}\) que el punto de equilibrio es una espiral. No obstante, en la Figura\(\PageIndex{2}\) es claro que la solución no sale en espiral hacia el infinito. Está delimitado por un círculo.
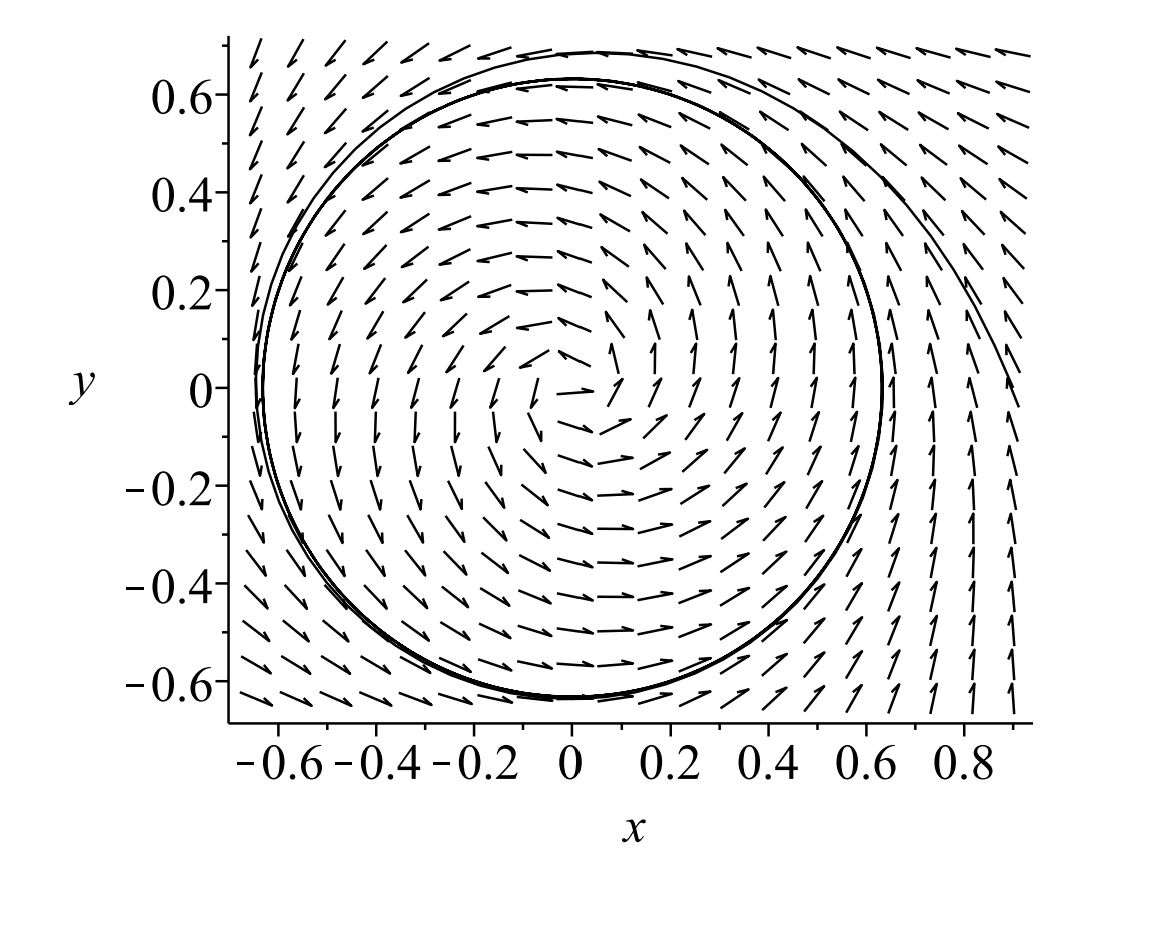
En realidad se puede encontrar el radio de este círculo. Esto requiere reescribir el sistema en forma polar. Recordemos del Capítulo 2 que podemos cambiar derivadas de coordenadas cartesianas a derivadas de coordenadas polares mediante el uso de las relaciones
\[r r^{\prime} =x x^{\prime}+y y^{\prime} \nonumber \]
\[r^{2} \theta^{\prime} =x y^{\prime}-y x^{\prime} \nonumber \]
Insertando el sistema\(\PageIndex{2}\) en estas expresiones, tenemos
\[r r^{\prime}=\mu r^{2}-r^{4}, \quad r^{2} \theta^{\prime}=r^{2}. \nonumber \]
Esto lleva al sistema
\[ \begin{aligned} r^{\prime} &=\mu r-r^{3}, \\ \theta^{\prime} &=1 . \end{aligned}\label{7.52} \]
Por supuesto, para un círculo el radio es constante,\(r=\) const. Por lo tanto, para encontrar el ciclo límite, necesitamos mirar las soluciones de equilibrio de la Ecuación\(\PageIndex{6}\). Esto equivale a encontrar las soluciones constantes de\(\mu r-r^{3}=0 .\) Las soluciones de equilibrio son\(r=0, \pm \sqrt{\mu} .\) El ciclo límite corresponde a la solución de radio positivo,\(r=\sqrt{\mu}\).
En Cifras\(\PageIndex{1} - \PageIndex{2}\) tomamos\(\mu=0.4\). En este caso esperamos un círculo con\(r=\sqrt{0.4} \approx 0.63\). De la\(\theta\) ecuación, tenemos eso\(\theta^{\prime}>0\). Esto significa que seguimos el ciclo límite en sentido contrario a las agujas del reloj a medida que aumenta el tiempo.
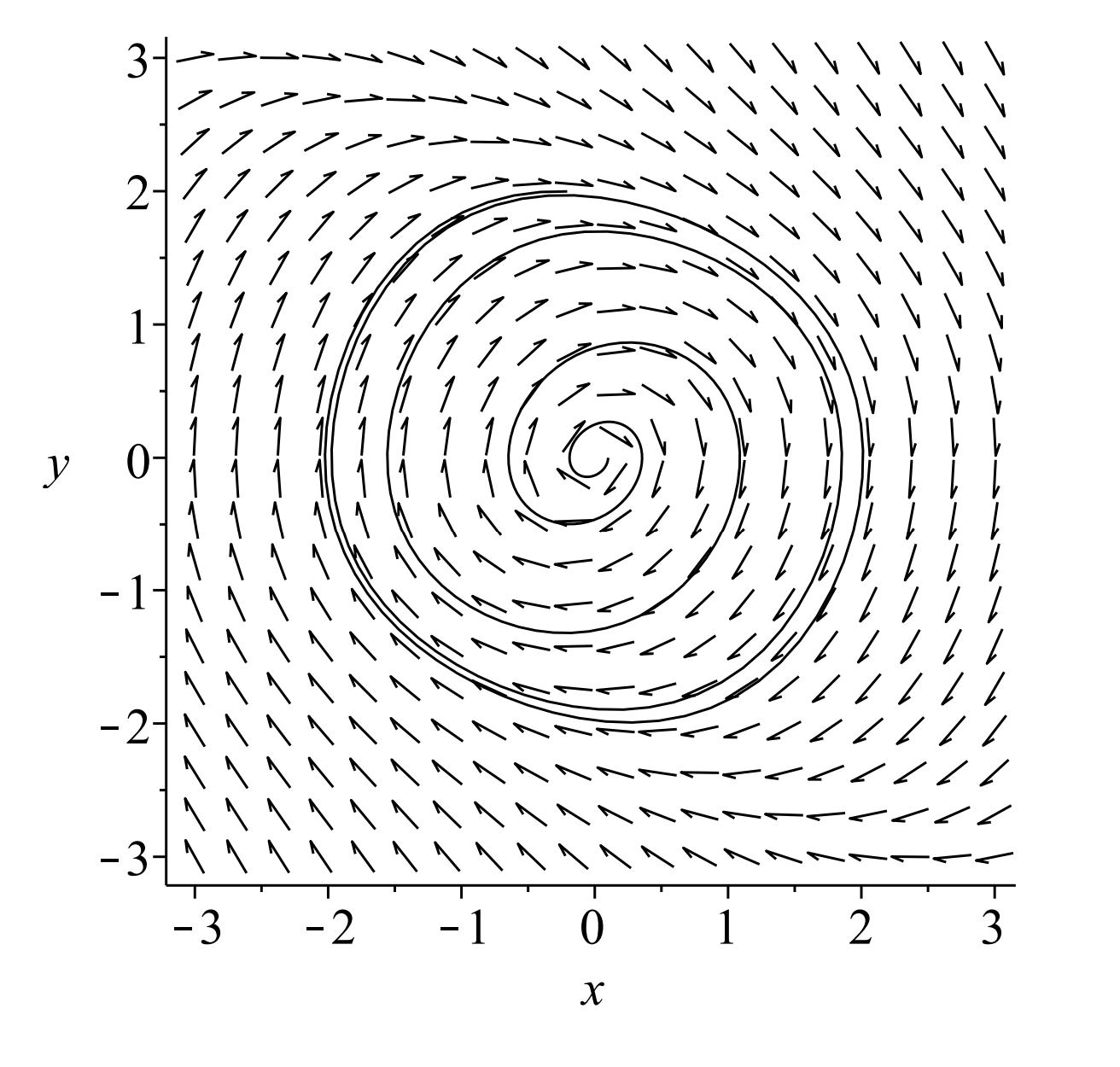
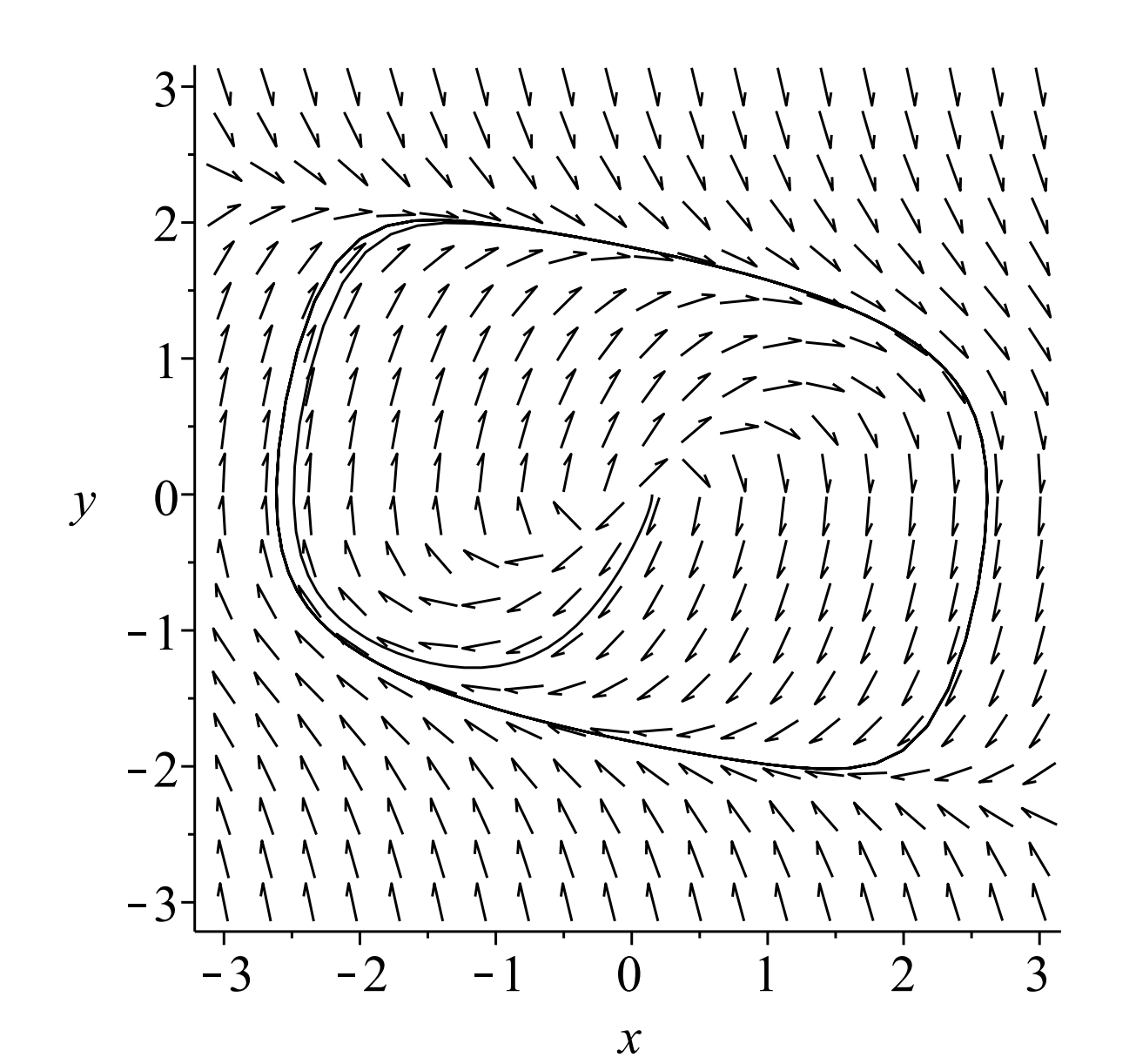
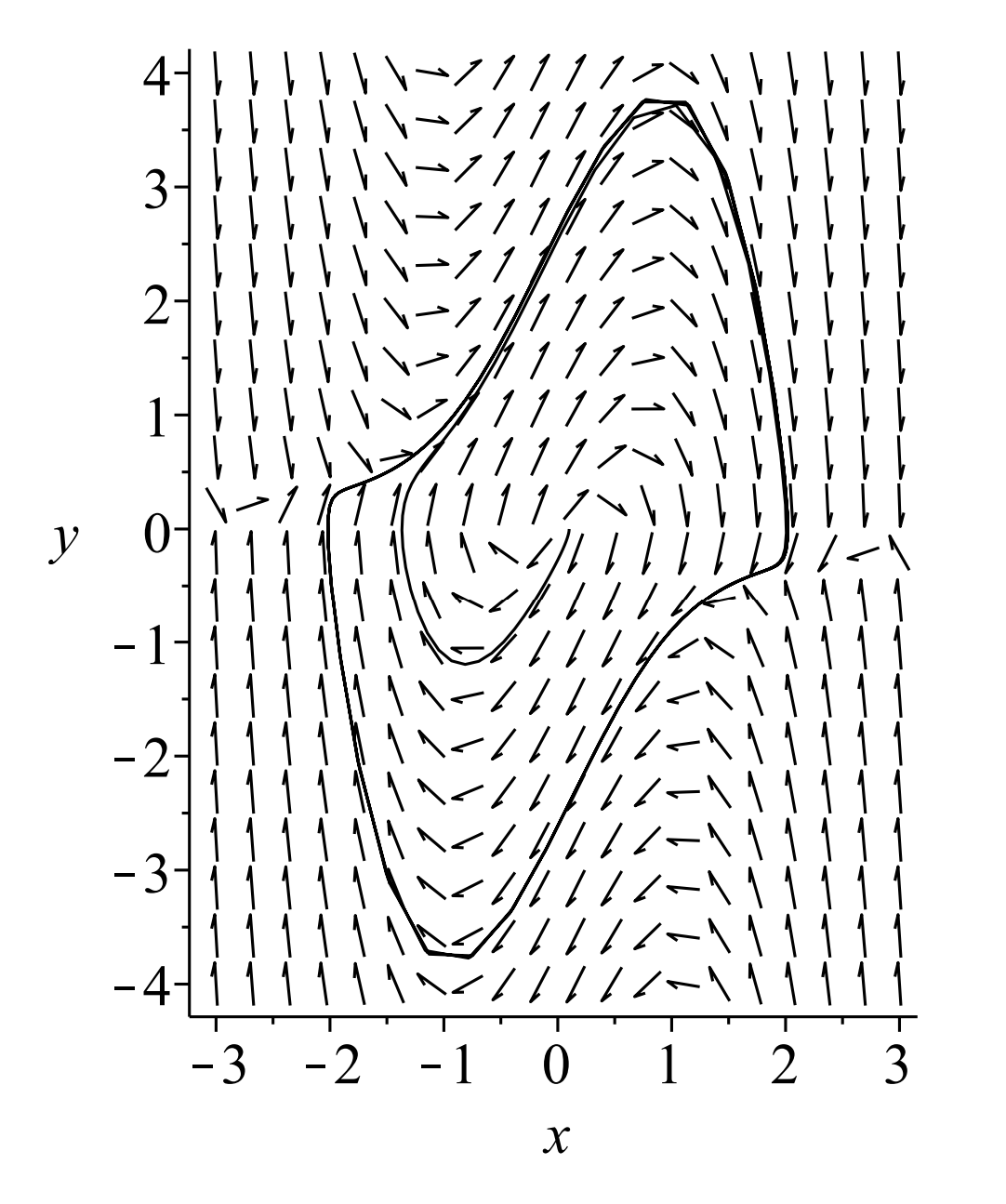
Los ciclos límite no son siempre círculos. En Figuras\(\PageIndex{3} -\PageIndex{4}\) mostramos el comportamiento del sistema Rayleigh\(\PageIndex{1}\) para\(c=0.4\) y\(c=2.0 .\) En este caso vemos que las soluciones tienden hacia un ciclo límite no circular en sentido horario.
Un ligero cambio del sistema Rayleigh lleva a la ecuación de van der Pol:
\[x^{\prime \prime}+c\left(x^{2}-1\right) x^{\prime}+x=0 \nonumber \]
(El sistema van der Pol). El ciclo límite para\(c=2.0\) se muestra en la Figura\(\PageIndex{5}\).
¿Se puede determinar con anticipación si un sistema no lineal dado tendrá un ciclo límite? Para responder a esta pregunta, introduciremos algunas definiciones.
Primero describimos diferentes trayectorias y familias de trayectorias. Un flujo encendido\(R^{2}\) es una función\(\phi\) que satisface lo siguiente
- \(\phi(\mathbf{x}, t)\)es continuo en ambos argumentos.
- \(\phi(\mathbf{x}, 0)=\mathbf{x}\)para todos\(\mathbf{x} \in R^{2}\).
- \(\phi\left(\phi\left(\mathbf{x}, t_{1}\right), t_{2}\right)=\phi\left(\mathbf{x}, t_{1}+t_{2}\right)\).
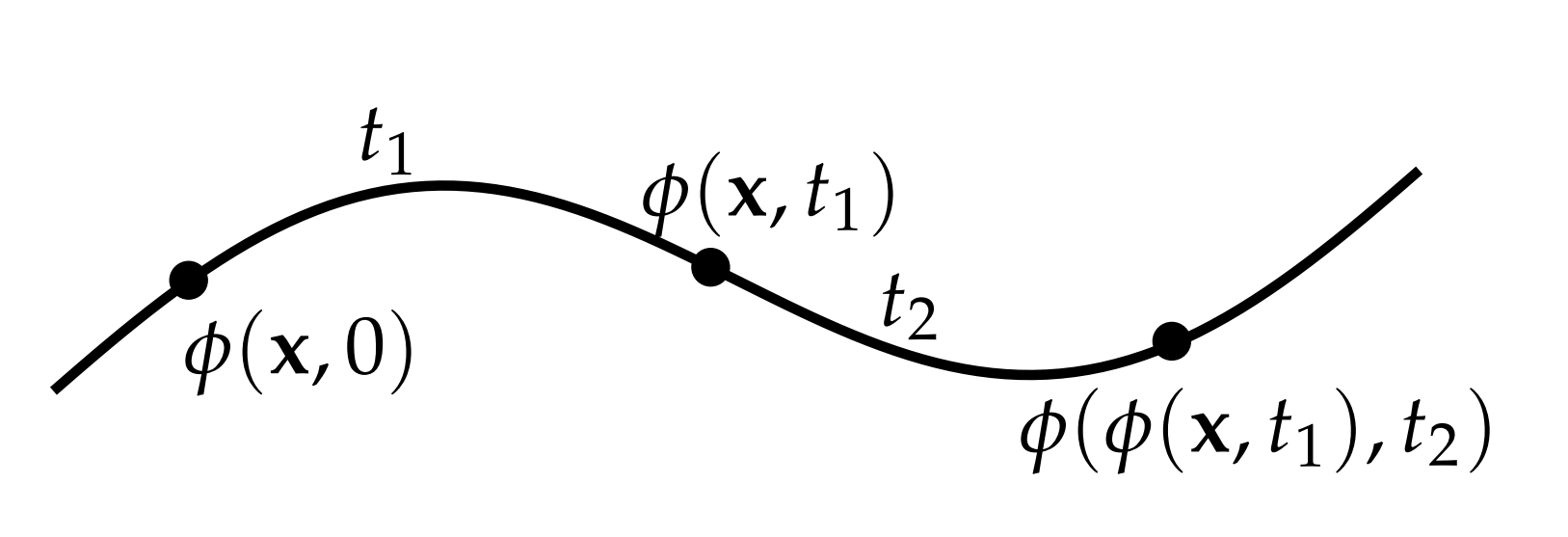
(Órbitas y trayectorias). La órbita, o trayectoria, a través\(\mathbf{x}\) se define como\(\gamma=\{\phi(\mathbf{x}, t) \mid t \in I\} .\) En la Figura\(\PageIndex{6}\) demostramos estas propiedades. Para\(t=0, \phi(\mathbf{x}, 0)=\mathbf{x}\). Al aumentar\(t\), se sigue la trayectoria hasta llegar al punto\(\phi\left(\mathbf{x}, t_{1}\right)\). Continuando\(t_{2}\) más, uno está entonces en\(\phi\left(\phi\left(\mathbf{x}, t_{1}\right), t_{2}\right)\). Por la tercera propiedad, esto es lo mismo que ir de\(\mathbf{x}\) a\(\phi\left(\mathbf{x}, t_{1}+t_{2}\right)\) para\(t=t_{1}+t_{2}\).
Una vez definidas las órbitas, necesitamos definir el comportamiento asintótico de la órbita tanto para tiempos grandes positivos como negativos. Definimos la semiórbita positiva a través\(\mathbf{x}\) como\(\gamma^{+}=\{\phi(\mathbf{x}, t) \mid t>0\} .\) La semiórbita negativa a través\(\mathbf{x}\) se define como\(\gamma^{-}=\{\phi(\mathbf{x}, t) \mid t<0\} .\) Así, tenemos\(\gamma=\gamma^{+} \cup \gamma^{-}\).
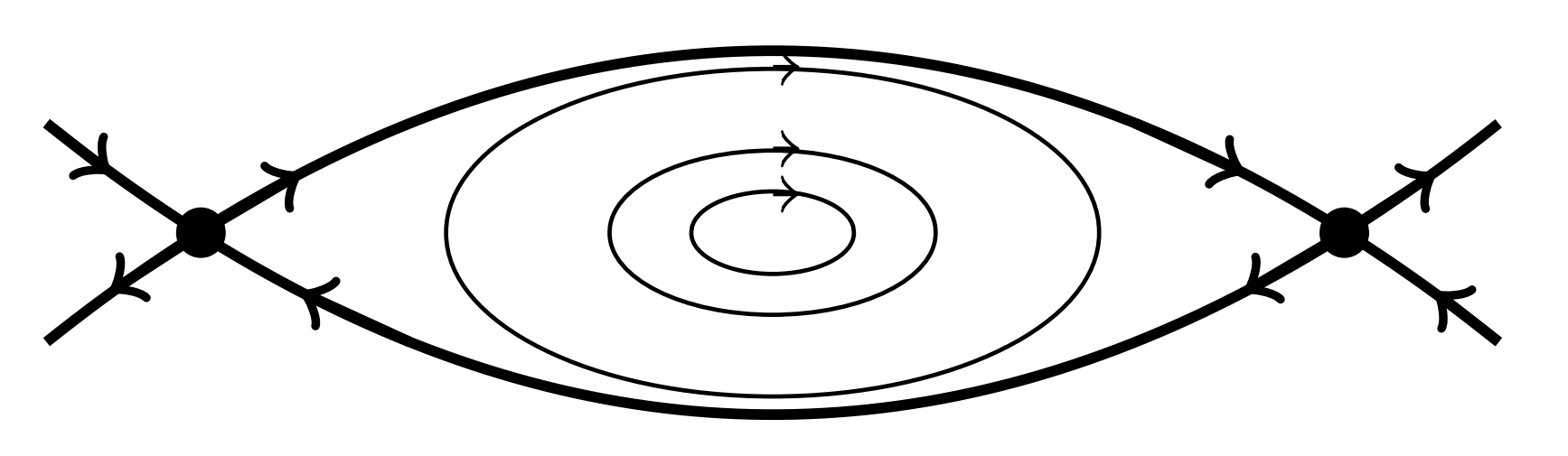
(Conjuntos de límites y puntos límite). El conjunto de límite positivo, o conjunto de límite w, de punto\(\mathbf{x}\) se define como
\[\Lambda^{+}=\left\{\mathbf{y} \mid \text { there exists a sequence of } t_{n} \rightarrow \infty \text { such that } \phi\left(\mathbf{x}, t_{n}\right) \rightarrow \mathbf{y}\right\} \nonumber \]
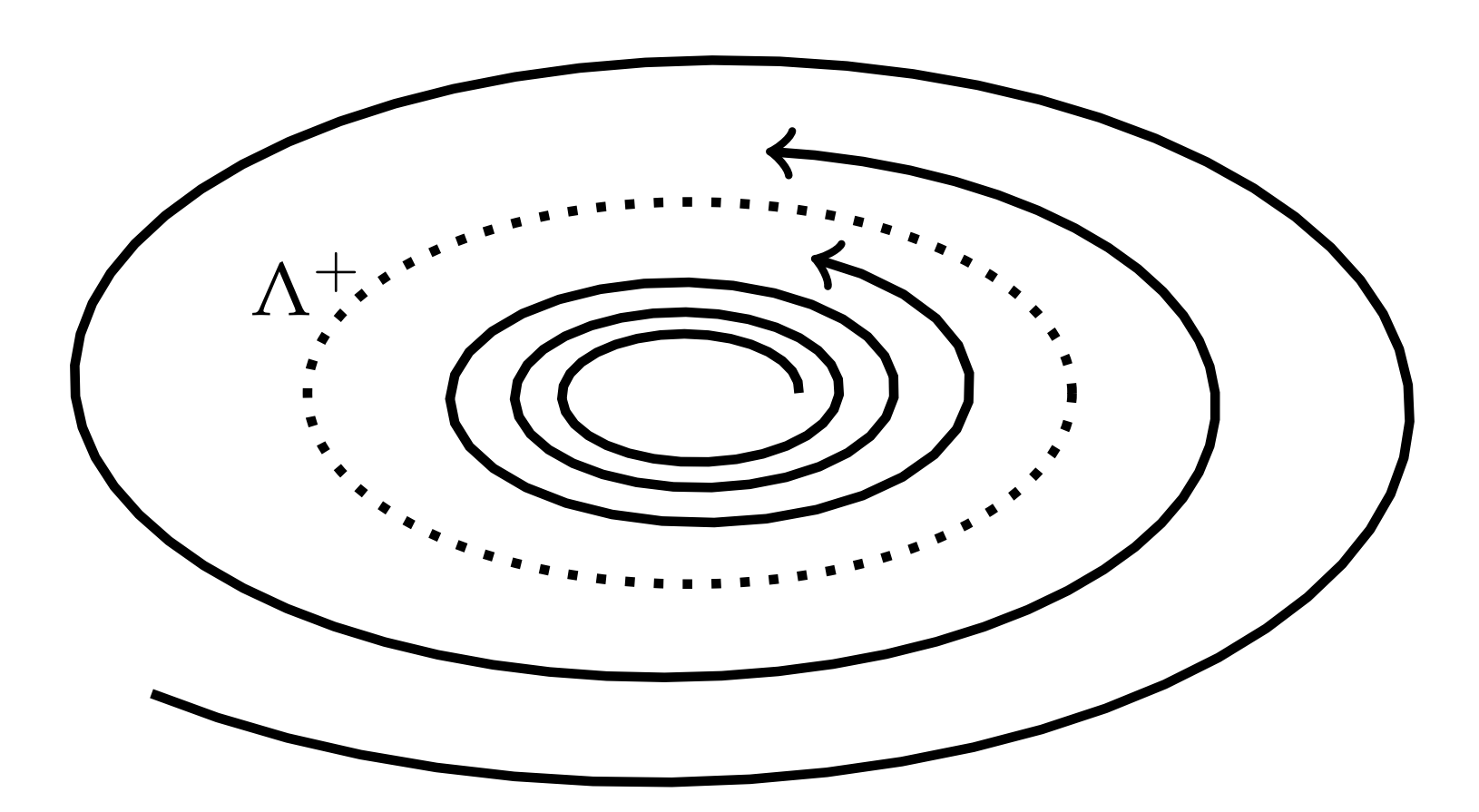
Los\(\mathbf{y}^{\prime}\) s se conocen como puntos w-limit. Esto se muestra en la Figura\(\PageIndex{7}\).
Del mismo modo, definimos el conjunto de límite negativo, o el conjunto de límite alfa, de punto\(\mathbf{x}\) se define como
\[\Lambda^{-}=\left\{\mathbf{y} \mid \text { there exists a sequences of } t_{n} \rightarrow-\infty \text { such that } \phi\left(\mathbf{x}, t_{n}\right) \rightarrow \mathbf{y}\right\}\nonumber \]
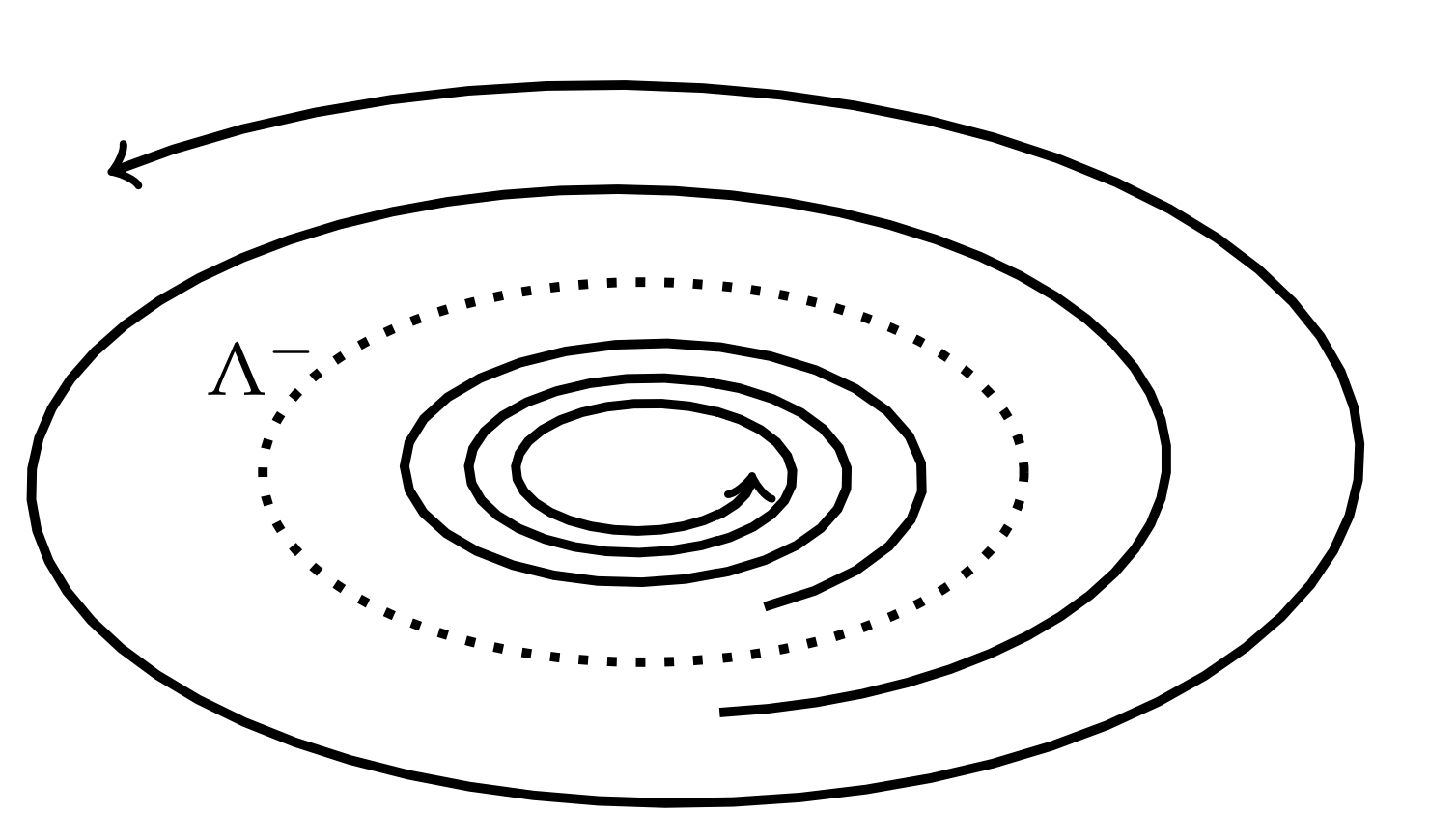
y las\(\mathbf{y}^{\prime}\) s correspondientes son\(\alpha\) -puntos límite. Esto se muestra en la Figura\(\PageIndex{8}\).
(Ciclos y órbitas periódicas). Hay varios tipos de órbitas que un sistema podría poseer. Un ciclo u órbita periódica es cualquier órbita cerrada que no es un punto de equilibrio. Una órbita periódica es estable si por cada vecindad de la órbita tal que todas las órbitas cercanas permanezcan dentro del vecindario. De lo contrario, es inestable. La órbita es asintóticamente estable si todas las órbitas cercanas convergen a la órbita periódica.
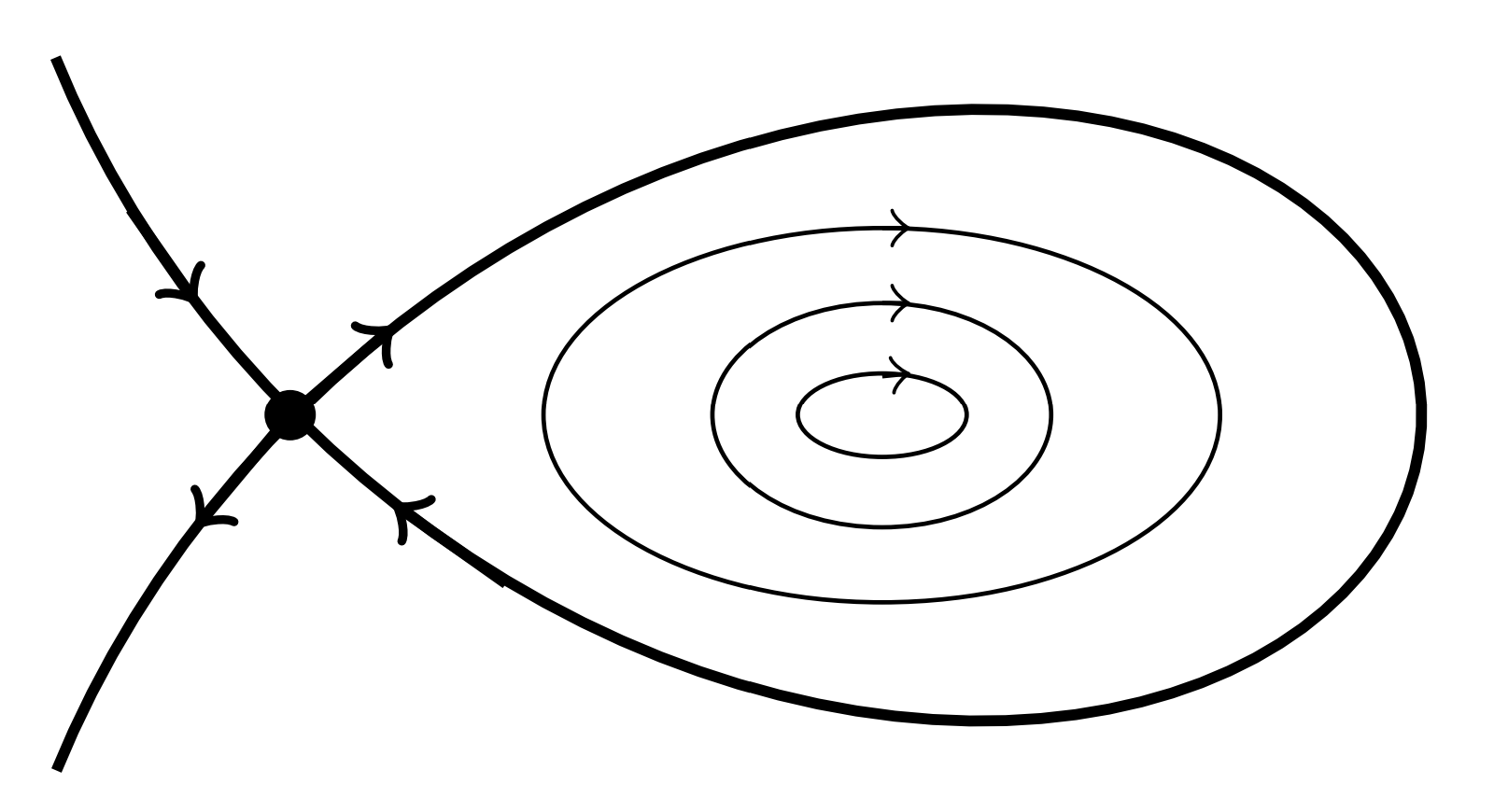
Un ciclo límite es un ciclo que es el conjunto\(\alpha\) o\(\omega\) -limit de alguna trayectoria que no sea el ciclo límite. Un ciclo límite\(\Gamma\) es estable si\(\Lambda^{+}=\Gamma\) para todos\(\mathbf{x}\) en algún barrio de\(\Gamma\). Un ciclo límite\(\Gamma\) es inestable si\(\Lambda^{-}=\Gamma\) para todos\(\mathbf{x}\) en algún vecindario de\(\Gamma\). Por último, un ciclo límite es semistable si está atrayendo por un lado y repeliendo por el otro lado. En los ejemplos anteriores, vimos ciclos límite que eran estables. Las figuras\(\PageIndex{7}\) y\(\PageIndex{8}\) representan ciclos límite estables e inestables, respectivamente.
Ahora declaramos un teorema que describe el tipo de órbitas que podríamos encontrar en nuestro sistema.
\(\gamma^{+}\)Déjese contener en región\(a\) acotada en la que hay finitamente muchos puntos críticos. Entonces\(\Lambda^{+}\) es
- un único punto crítico;
- una sola órbita cerrada;
- un conjunto de puntos críticos unidos por órbitas heteroclínicas. [Comparar cifras\(\PageIndex{9}\) y\(\PageIndex{10}.\)]
Nos interesa determinar cuándo pueden existir, o no, ciclos límite. Una consecuencia del Teorema de Poincaré-Bendixon viene dada por el siguiente corolario.
Dejar\(D\) ser un conjunto cerrado acotado que no contiene puntos críticos y supongamos que\(\gamma^{+} \subset D .\) Entonces existe un ciclo límite contenido en\(D .\)
Criterios más específicos nos permiten determinar si existe un ciclo límite en una región determinada. Estos están dados por Criterios de Dulac y Criterios de Bendixon.
Considere el sistema plano autónomo
\[x^{\prime}=f(x, y), \quad y^{\prime}=g(x, y)\nonumber \]
y una función continuamente diferenciable\(\psi\) def
\(D\) contenida en algún conjunto abierto. Si
\[\dfrac{\partial}{\partial x}(\psi f)+\dfrac{\partial}{\partial y}(\psi g) \nonumber \]
no cambia de inicio de sesión\(D\), entonces hay como máximo un ciclo límite contenido completamente en\(D .\)
Considere el sistema plano autónomo
\[x^{\prime}=f(x, y), \quad y^{\prime}=g(x, y)\nonumber \]
definido en un dominio simplemente conectado de\(D\) tal manera que
\[\dfrac{\partial}{\partial x}(\psi f)+\dfrac{\partial}{\partial y}(\psi g) \neq 0 \nonumber \]
en\(D\). Entonces, no hay ciclos límite enteramente en\(D\).
- Comprobante.
-
Estos se prueban fácilmente usando el Teorema de Green en el Plano. (Consulte el texto de su cálculo.) Demostramos los Criterios de Bendixon. Vamos\(\mathbf{f}=(f, g)\). Supongamos que\(\Gamma\) es una órbita cerrada que se encuentra en\(D .\) Let\(S\) be the interior of\(\Gamma .\) then
\[ \begin{aligned} \int_{S} \nabla \cdot \mathbf{f} d x d y &=\oint_{\Gamma}(f d y-g d x) \\ &=\int_{0}^{T}(f \dot{y}-g \dot{x}) d t \\ &=\int_{0}^{T}(f g-g f) d t=0 . \end{aligned} \label{7.54} \]
Entonces, si no\(\nabla \cdot \mathbf{f}\) es idénticamente cero y no cambia de inicio de sesión\(S\), entonces desde la continuidad de\(\nabla \cdot \mathbf{f}\) adentro\(S\) tenemos que el lado derecho arriba es positivo o negativo. Así, tenemos una contradicción y no hay una órbita cerrada que se encuentra en\(D\).
Considera el ejemplo anterior en\((7 \cdot 48)\) con\(\mu=1\).
\[ \begin{aligned} &x^{\prime}=x-y-x\left(x^{2}+y^{2}\right) \\ &y^{\prime}=x+y-y\left(x^{2}+y^{2}\right) \end{aligned} \label{7.55} \]
Ya sabemos que existe un ciclo límite en\(x^{2}+y^{2}=1 .\) Un simple cálculo da que
\[\nabla \cdot \mathbf{f}=2-4 x^{2}-4 y^{2} \nonumber \]
Para un anillo arbitrario\(a<x^{2}+y^{2}<b\), tenemos
\[2-4 b<\nabla \cdot \mathbf{f}<2-4 a \nonumber \]
Para\(a=3 / 4\) y\(b=5 / 4,-3<\nabla \cdot \mathbf{f}<-1\). Así,\(\nabla \cdot \mathbf{f}<0\) en el anillo\(3 / 4<x^{2}+y^{2}<5 / 4\). Por lo tanto, por Criterios de Dulac hay como máximo un ciclo límite en este anillo.
Considerar el sistema
\[ \begin{aligned} &x^{\prime}=y \\ &y^{\prime}=-a x-b y+c x^{2}+d y^{2} . \end{aligned} \label{7.56} \]
Vamos\(\psi(x, y)=e^{-2 d x} .\) Entonces,
\[\dfrac{\partial}{\partial x}(\psi y)+\dfrac{\partial}{\partial y}\left(\psi\left(-a x-b y+c x^{2}+d y^{2}\right)\right)=-b e^{-2 d x} \neq 0 \nonumber \]
Concluimos por Criterios de Bendixon que no hay ciclos límite para este sistema.


