7.8: Sistemas no autónomos no lineales
- Page ID
- 119687
EN ESTA SECCIÓN SE DISCUTEN LOS SISTEMAS NO AUTÓNOMOS. Recordemos que un sistema autónomo es aquel en el que no existe una dependencia explícita del tiempo. Un ejemplo sencillo es el péndulo no lineal forzado dado por la ecuación no homogénea
\[\ddot{x}+\omega^{2} \sin x=f(t) \nonumber \]
Podemos configurarlo como un sistema de dos ecuaciones de primer orden:
\[ \begin{aligned} &\dot{x}=y \\ &\dot{y}=-\omega^{2} \sin x+f(t) . \end{aligned} \label{7.58} \]
Este sistema no está en una forma para la que pudiéramos utilizar los métodos anteriores. Es decir, se trata de un sistema no autónomo. Sin embargo, introducimos una nueva variable\(z(t)=t\) y la convertimos en un sistema autónomo en una dimensión más. El nuevo sistema toma la forma
\[ \begin{aligned} \dot{x} &=y \\ \dot{y} &=-\omega^{2} \sin x+f(z) . \\ \dot{z} &=1 . \end{aligned} \label{7.59} \]
El sistema es ahora un sistema autónomo tridimensional, posiblemente no lineal, y se puede explorar utilizando métodos de los Capítulos 2 y 3.
Un modelo más interesante es proporcionado por la Ecuación Duffing. Esta ecuación, que lleva el nombre de Georg Wilhelm Christian Caspar Duffing (1861-1944), modela las oscilaciones de resorte duro y resorte blando. También modela una viga forzada periódicamente como se muestra en la Figura\(\PageIndex{1}\). Es de interés porque se trata de una ecuación simple que describe un método de visualización periódicamente forzados nuevos para sistemas no autónomos.
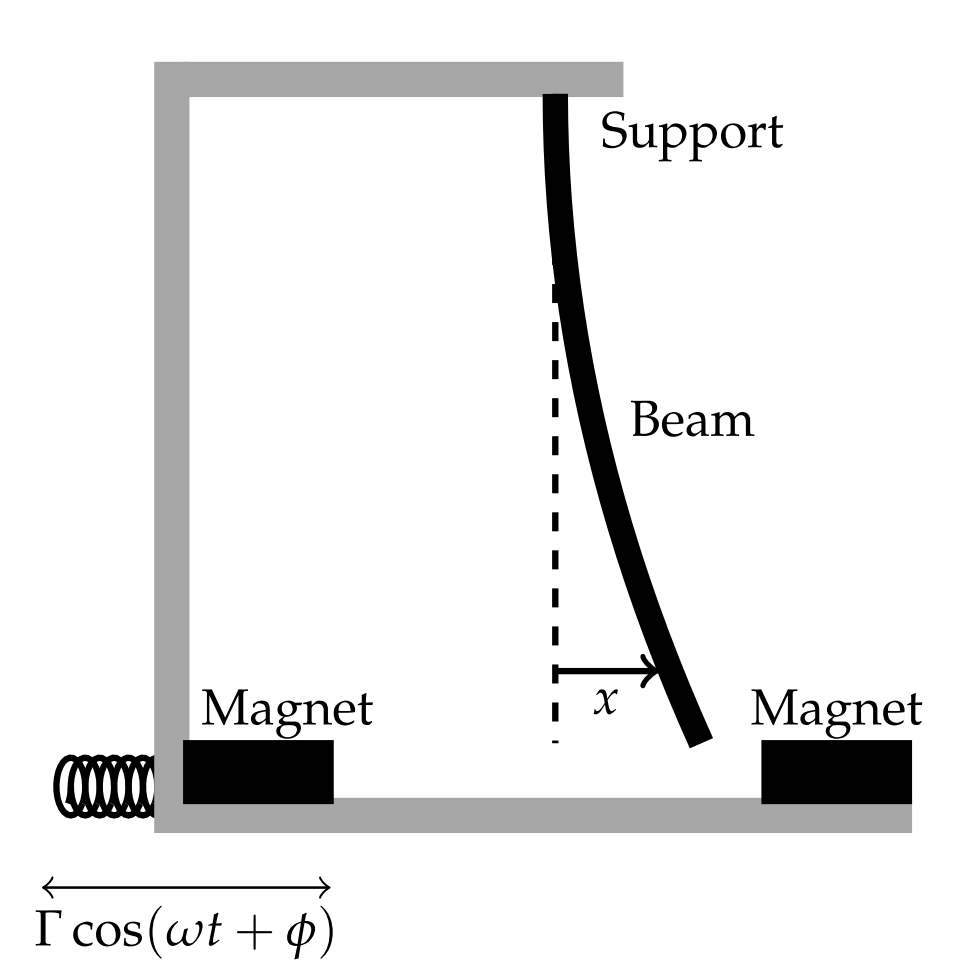
La forma más general de la ecuación de Duffing viene dada por el sistema amortiguado y forzado
\[\ddot{x}+k \dot{x}+\left(\beta x^{3} \pm \omega_{0}^{2} x\right)=\Gamma \cos (\omega t+\phi) . \nonumber \]
Esta ecuación modela las oscilaciones de resorte duro y resorte blando.\((\beta>0)\)\((\beta<0)\) Sin embargo, usaremos la versión más simple de la ecuación Duffing:
\[\ddot{x}+k \dot{x}+x^{3}-x=\Gamma \cos \omega t . \nonumber \]
Una ecuación de esta forma se puede obtener estableciendo\(\phi=0\) y reescalando\(x\) y\(t\) en la ecuación original. Exploraremos el comportamiento del sistema a medida que variamos los parámetros restantes. En las Figuras\(\PageIndex{2}-\PageIndex{5}\) se muestran algunas gráficas de solución típicas superpuestas sobre el campo de dirección.
(La ecuación de Duffing sin amortiguar y no forzada). Comenzamos con la ecuación de\((\Gamma=0)\) Duffing sin amortiguar\((k=0)\) y no forzada,
\[\ddot{x}+x^{3}-x=0 \nonumber \]
Podemos escribir esta ecuación de segundo orden como el sistema autónomo
\[ \begin{aligned} \dot{x} &=y \\ \dot{y} &=x\left(1-x^{2}\right) . \end{aligned} \label{7.62} \]
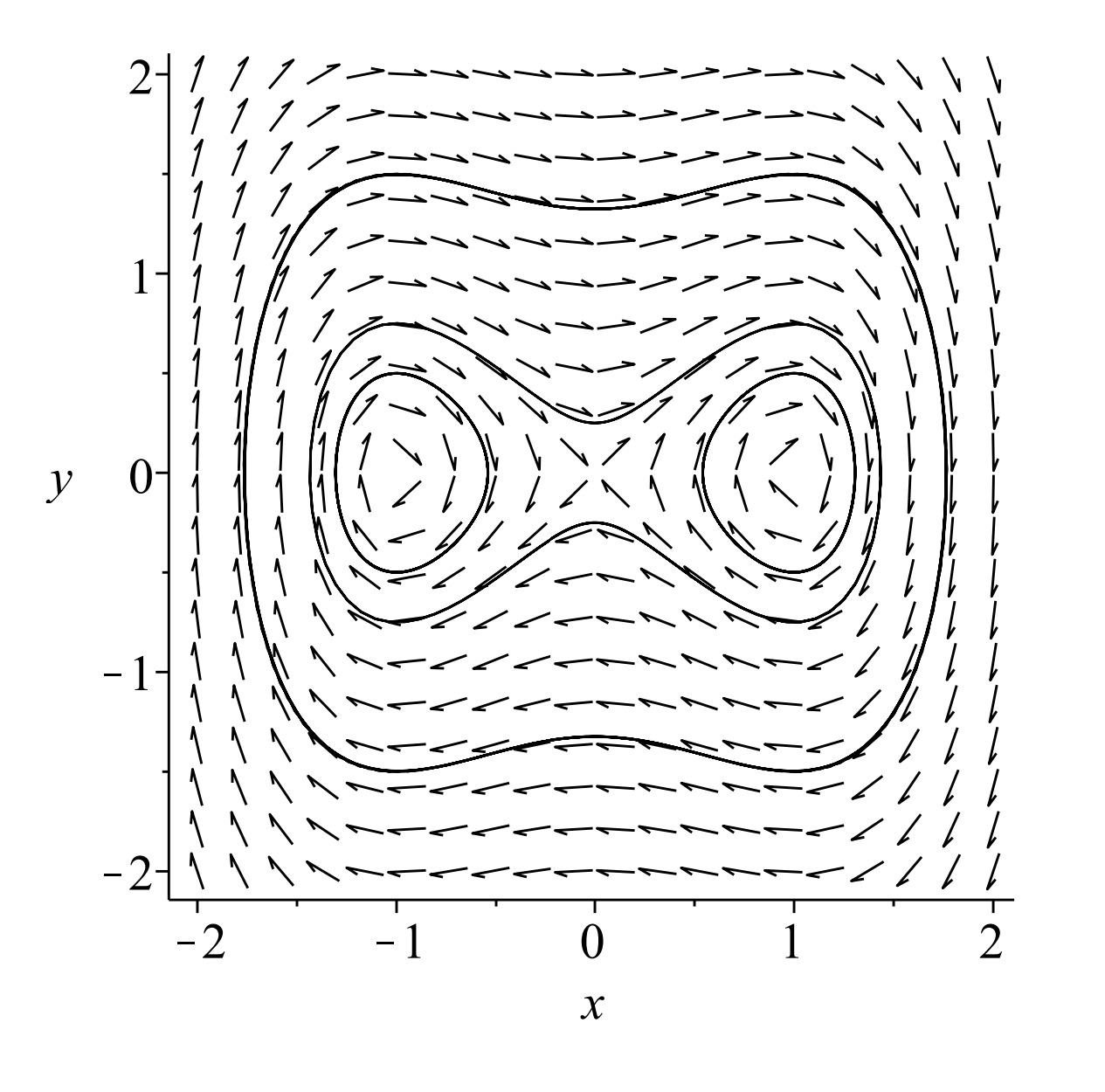
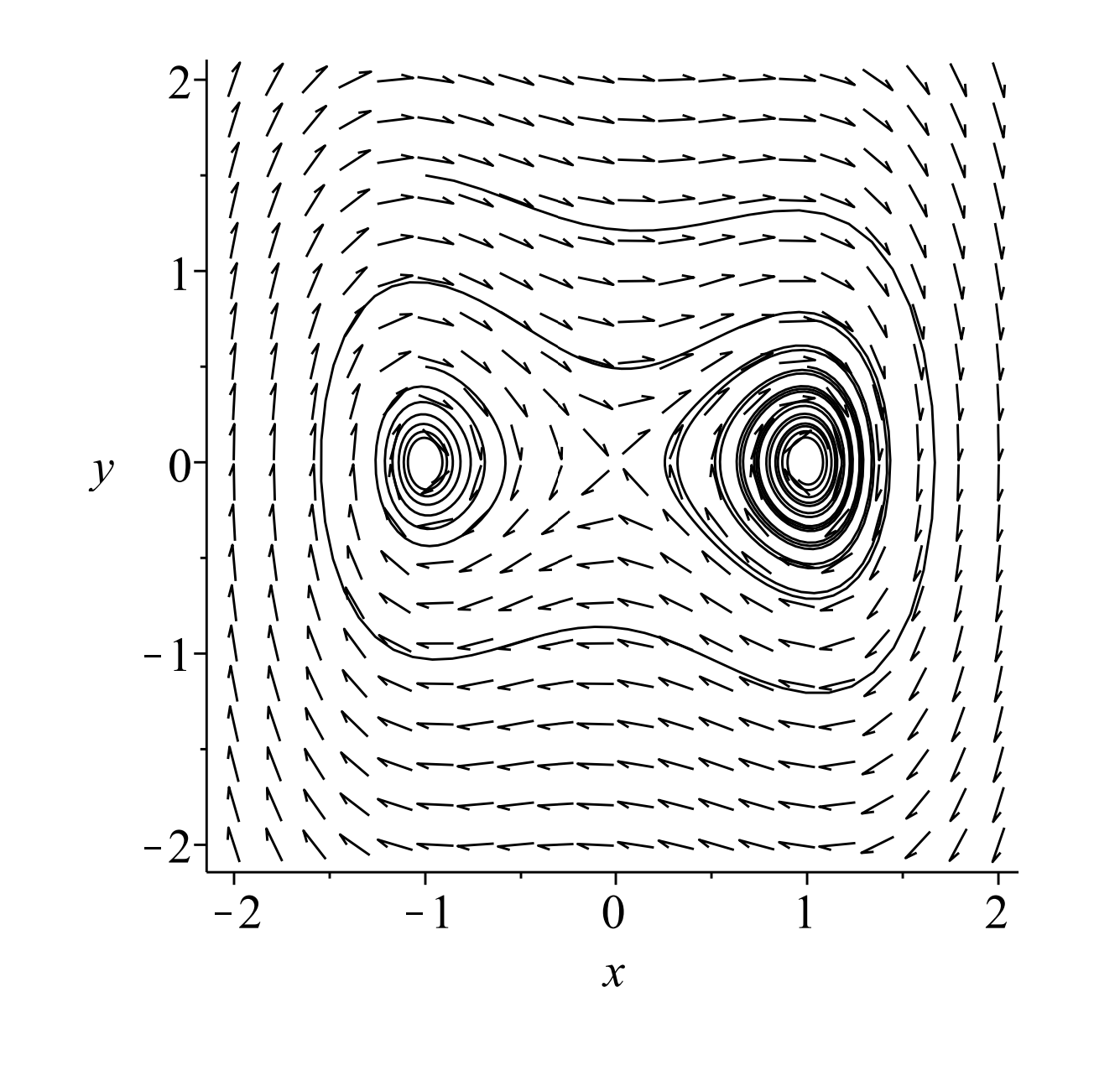
Vemos que hay tres puntos de equilibrio en\((0,0)\) y\((\pm 1,0) .\) En Figura\(\PageIndex{3}\) trazamos varias órbitas para\(k=0\), y\(\Gamma=0\). Vemos que los tres puntos de equilibrio constan de dos centros y una silla de montar.
(La ecuación de Duffing no forzada). Ahora encendemos la amortiguación. El sistema se convierte
\[ \begin{aligned} \dot{x} &=y \\ \dot{y} &=-k y+x\left(1-x^{2}\right) . \end{aligned} \label{7.63} \]
En Cifras\(\PageIndex{3}\) y\(\PageIndex{4}\) mostramos lo que sucede cuando\(k=0.1\). Estas parcelas recuerdan a las parcelas para el péndulo no lineal; sin embargo, hay menos equilibrios. Tenga en cuenta que los centros se convierten en espirales estables para\(k>0\).
A continuación encendemos el forzamiento para obtener una ecuación de Duffing amortiguada y forzada. El sistema es ahora no autónomo.
La ecuación de Duffing amortiguada y forzada.
\[ \begin{aligned} \dot{x} &=y \\ \dot{y} &=x\left(1-x^{2}\right)+\Gamma \cos \omega t . \end{aligned} \label{7.64} \]
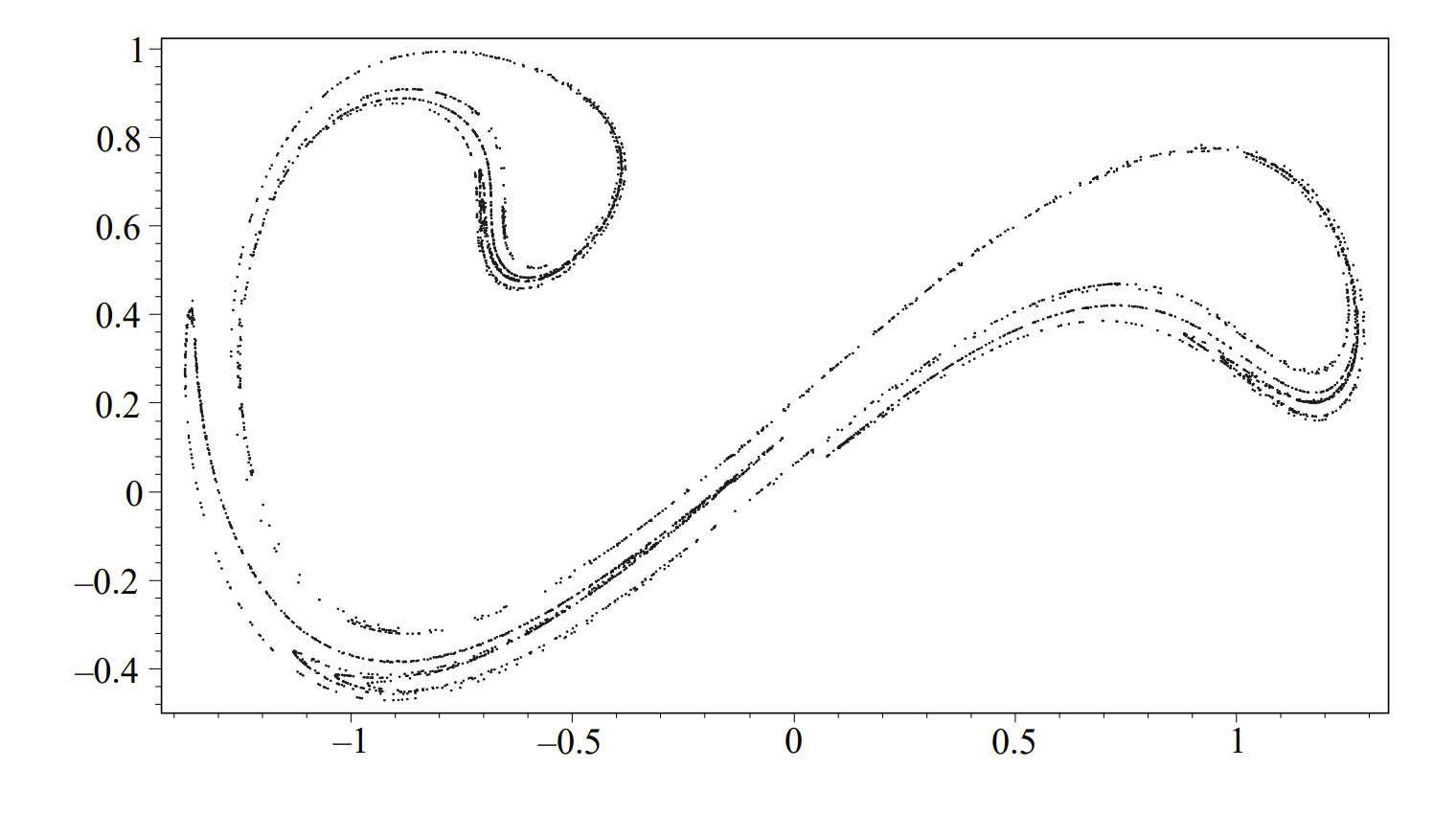
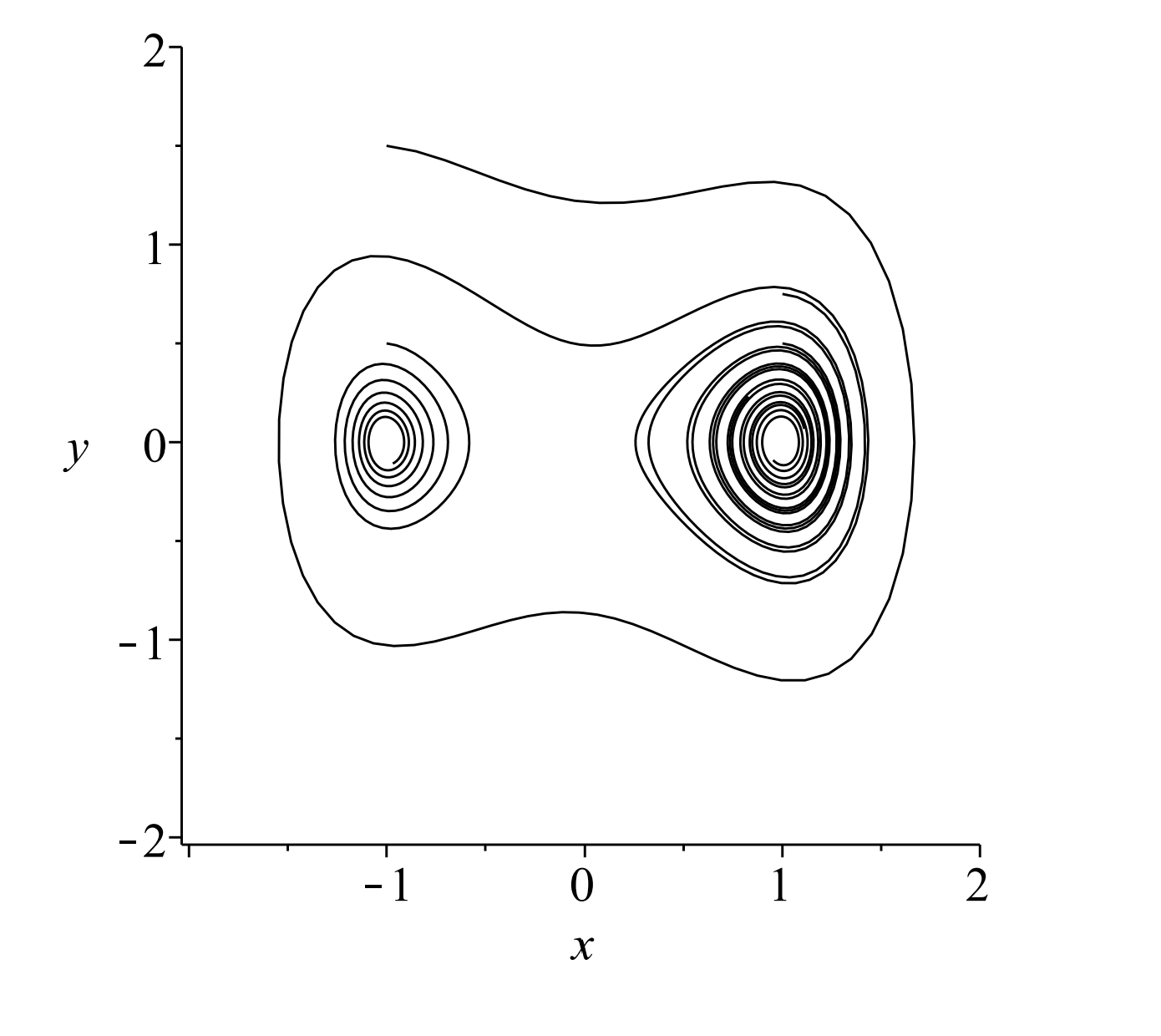
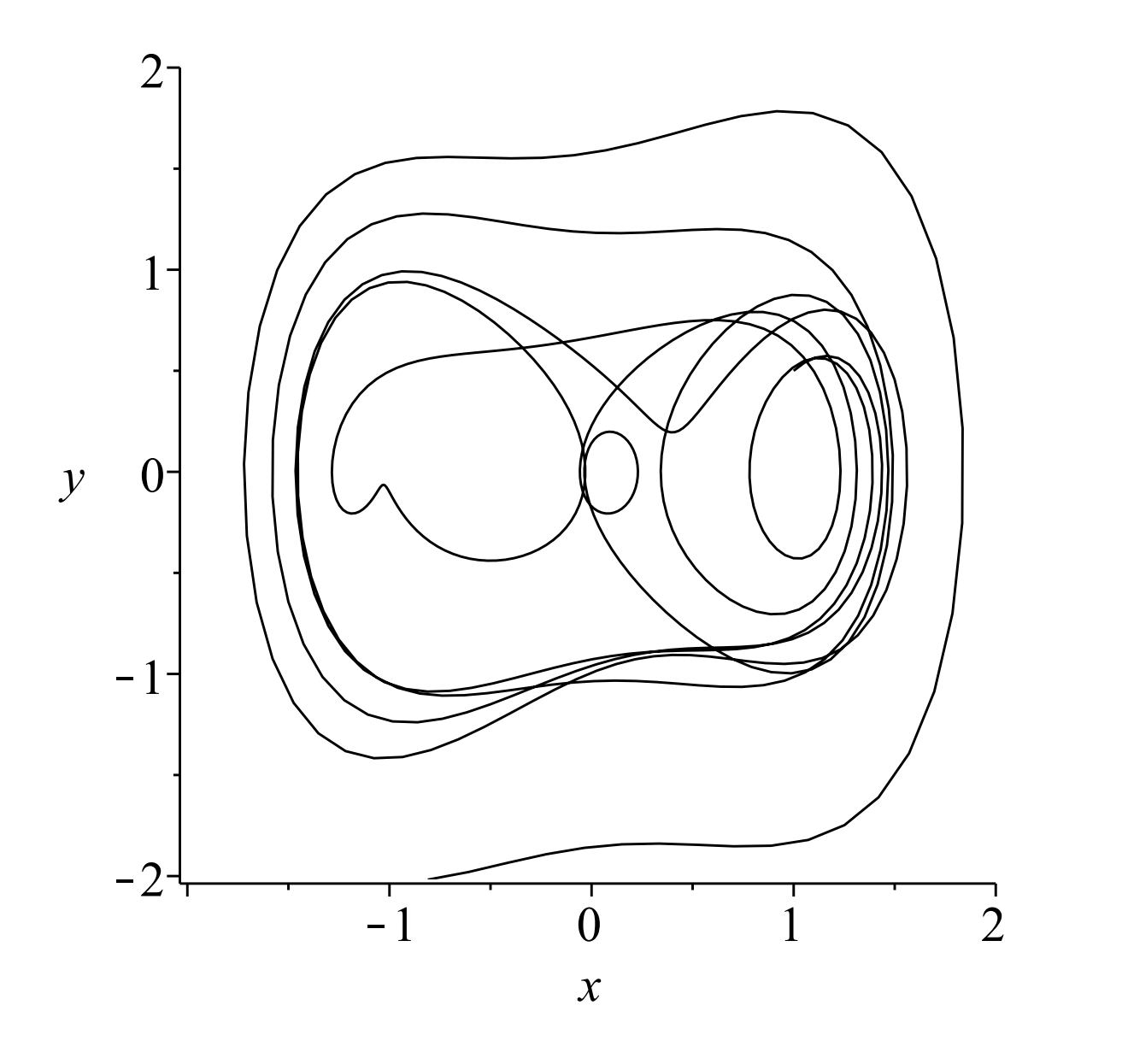
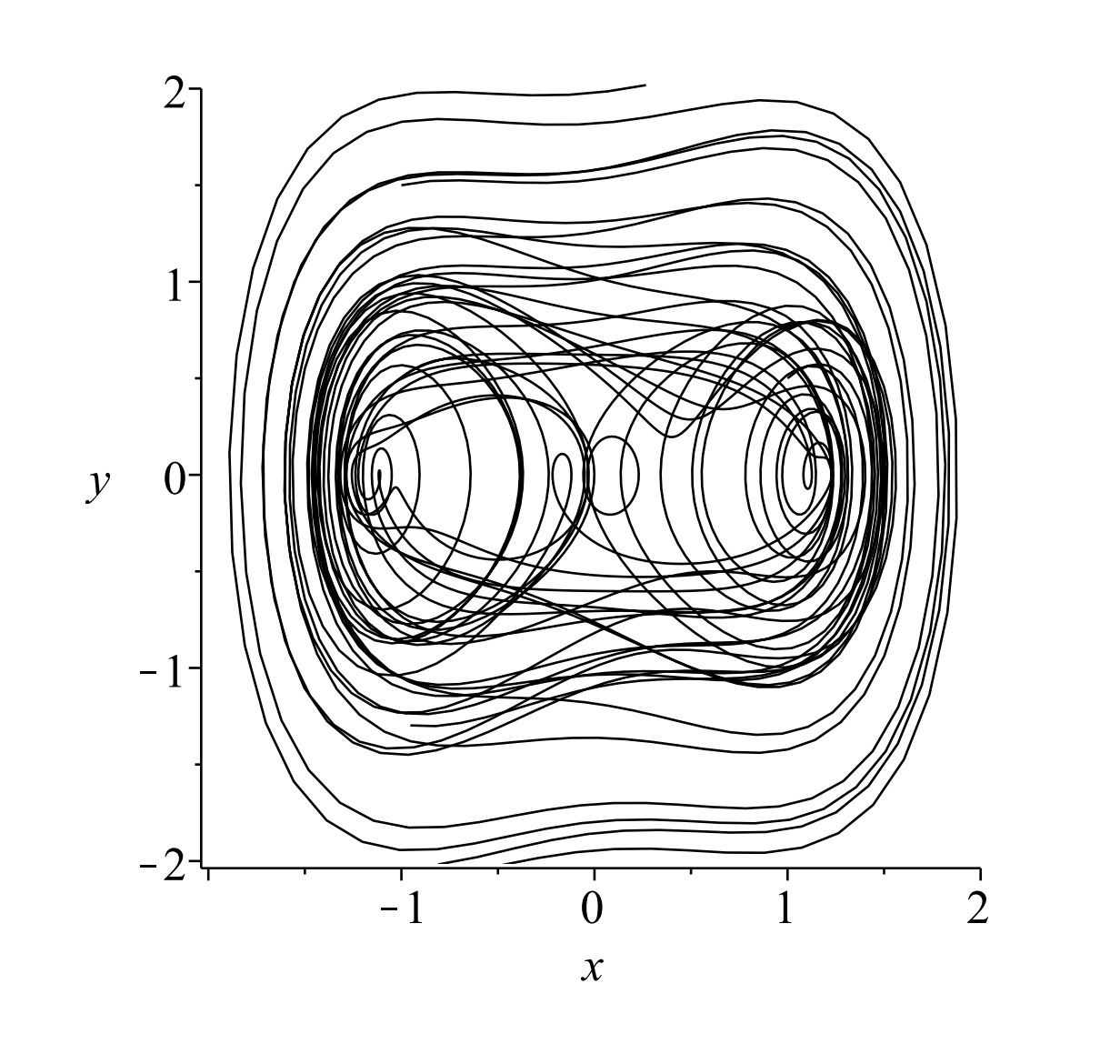
En la Figura solo\(\PageIndex{5}\) mostramos una órbita con\(k=0.1, \Gamma=0.5\), y\(\omega=1.25\). La solución se cruza y se ve un poco desordenada. Podemos imaginar lo que obtendríamos si agregáramos más órbitas. Para completar, mostramos en la Figura\(\PageIndex{6}\) un ejemplo con cuatro órbitas diferentes.
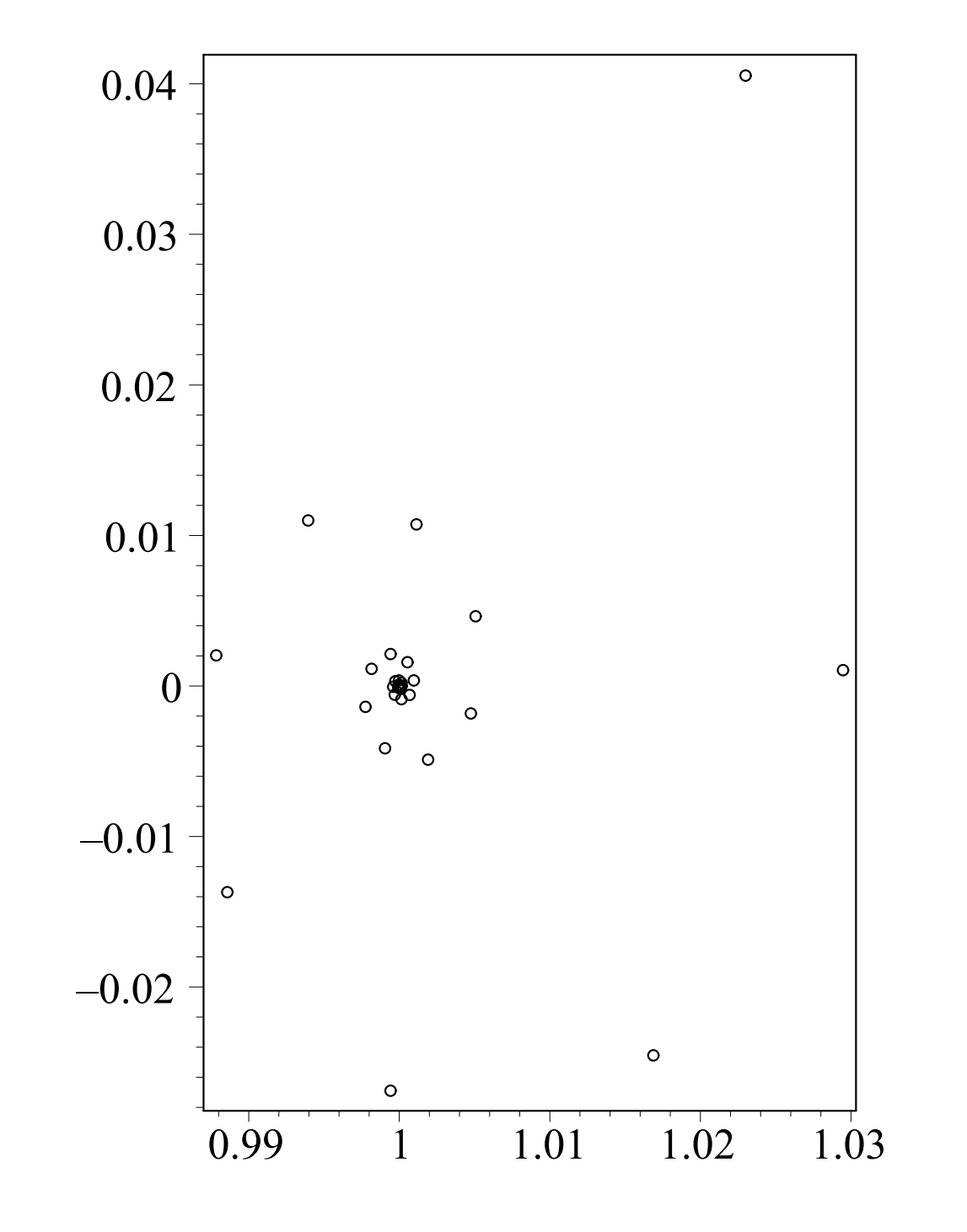
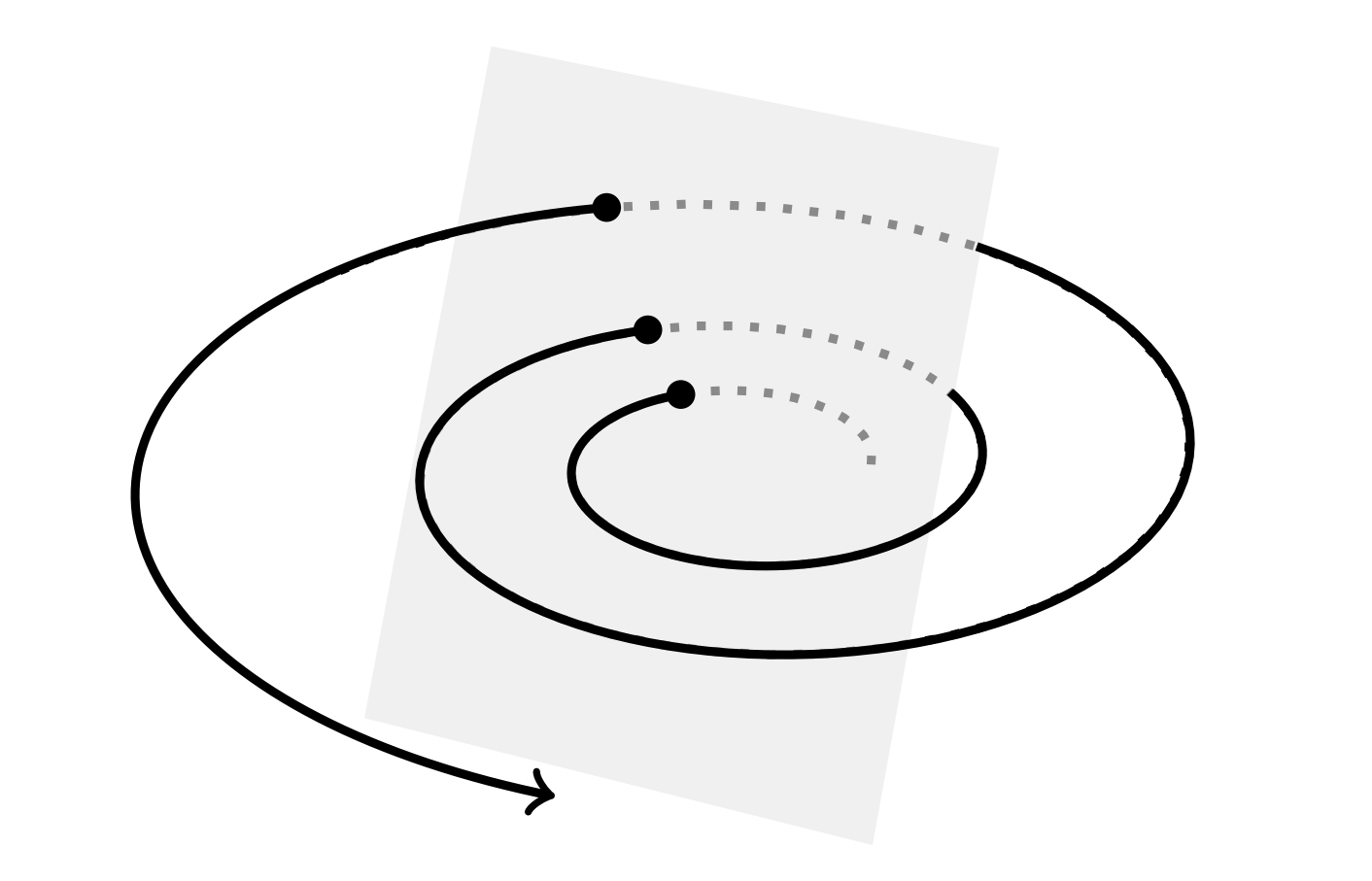
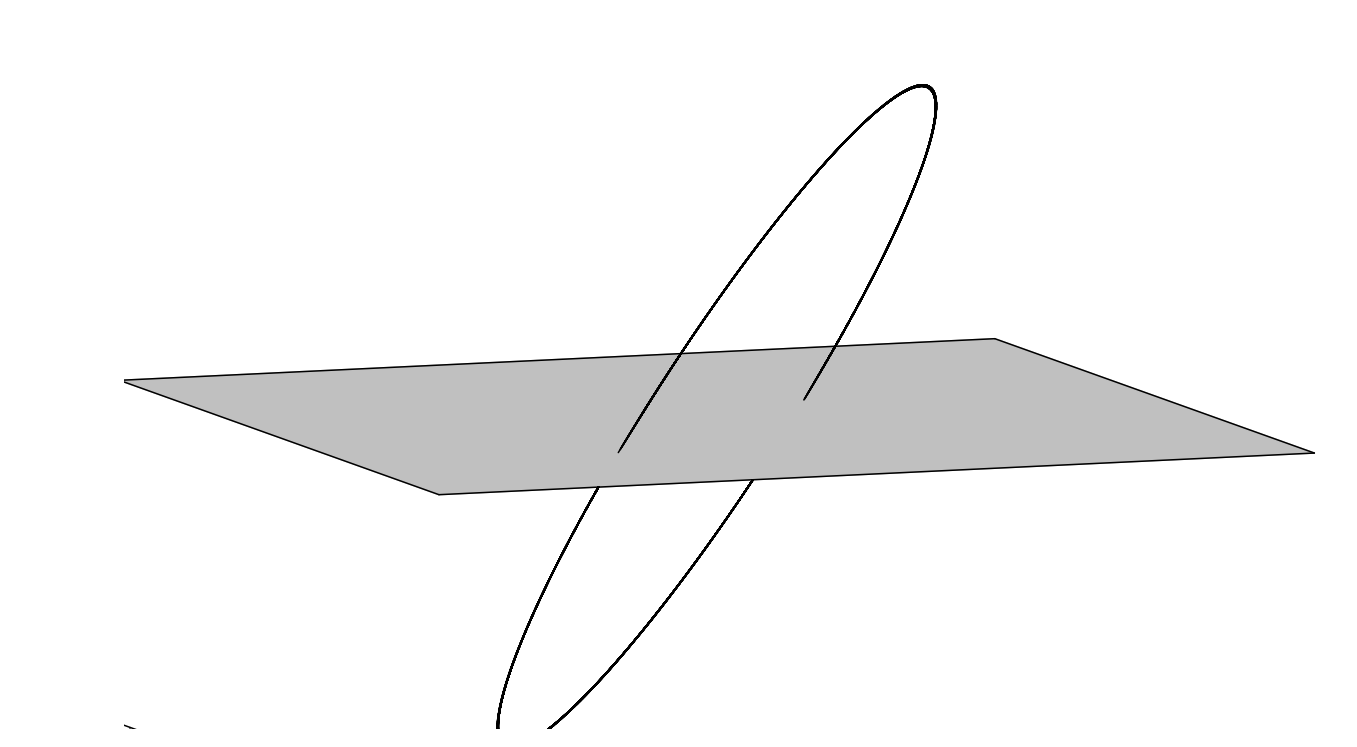
En los casos para los que se tienen órbitas periódicas como la ecuación Duffing, Poincaré introdujo la noción de superficies de sección. Uno incrusta la órbita en un espacio dimensional superior para que no haya autointersecciones, como vimos en Figuras\(\PageIndex{5}\) y\(\PageIndex{6}\). En la Figura\(\PageIndex{8}\) mostramos un ejemplo donde se muestra una órbita simple ya que perfora periódicamente una superficie determinada.
Para simplificar las imágenes resultantes, solo se trazan los puntos en los que la órbita perfora la superficie como se esboza en la Figura\(\PageIndex{7}\). En la práctica, hay una frecuencia natural, como\(\omega\) en la ecuación de Duffing forzado. Entonces, uno traza puntos en momentos que son múltiplos del periodo,\(T=\dfrac{2 \pi}{\omega} .\) En Figura\(\PageIndex{9}\) mostramos cómo sería la trama para una órbita para la ecuación de Duffing amortiguada y no forzada.
El caso más interesante, es cuando hay forzamiento y amortiguación. En este caso la superficie de la gráfica de sección se da en la Figura\(\PageIndex{10}\). Si bien esto no está tan ocupado como la gráfica de solución en la Figura\(\PageIndex{5}\), todavía proporciona algún comportamiento interesante. Lo que uno encuentra es lo que se llama un atractor extraño. Trazando muchas órbitas, encontramos que después de mucho tiempo, todas las órbitas son atraídas por una pequeña región en el plano, al igual que un nodo estable atrae órbitas cercanas. Sin embargo, este conjunto consta de más de un punto. Además, el flujo en el atractor es de naturaleza caótica. Así, los puntos deambulan de manera irregular por todo el atractor. Este es uno de los temas interesantes de la teoría del caos y toda esta teoría de los sistemas dinámicos solo ha sido tocada en este texto dejando al lector a vagar en mayor profundidad en este fascinante campo.
La superficie de las parcelas de sección al final de la última sección se obtuvo utilizando código del libro de S. Lynch Sistemas dinámicos con aplicaciones usando arce. Como referencia, las gráficas en Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\) se generaron en Maple usando los siguientes comandos: