7.10: Soluciones exactas usando funciones elípticas

LA SOLUCIÓN EN LA ECUACIÓN 7.9.9 DE LA ECUACIÓN DE PENDULO NO LINEAL condujo a la introducción de integrales elípticas. La integral elíptica incompleta del primer tipo se define como

\[F(\phi, k) \equiv \int_{0}^{\phi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}}=\int_{0}^{\sin \phi} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}} \nonumber \]

La integral completa del primer tipo viene dada por\(K(k)=F\left(\dfrac{\pi}{2}, k\right)\), o

\[K(k)=\int_{0}^{\pi / 2} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}}=\int_{0}^{1} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}} \nonumber \]

Las integrales elípticas del segundo tipo se definen como

\[E(\phi, k) =\int_{0}^{\phi} \sqrt{1-k^{2} \sin ^{2} \theta} d \theta=\int_{0}^{\sin \phi} \dfrac{\sqrt{1-k^{2} t^{2}}}{\sqrt{1-t^{2}}} d t \nonumber \]

\[E(k) =\int_{0}^{\pi / 2} \sqrt{1-k^{2} \sin ^{2} \theta} d \theta=\int_{0}^{1} \dfrac{\sqrt{1-k^{2} t^{2}}}{\sqrt{1-t^{2}}} d t \nonumber \]

Recordemos, una primera integración de la ecuación de péndulo no lineal a partir de la Ecuación 7.9.6.

\[\left(\dfrac{d \theta}{d t}\right)^{2}-\omega^{2} \cos \theta=-\omega^{2} \cos \theta_{0} \nonumber \]

O

\[\left(\dfrac{d \theta}{d t}\right)^{2}=2 \omega^{2}\left[\sin ^{2} \dfrac{\theta}{2}-\sin ^{2} \dfrac{\theta_{0}}{2}\right]\nonumber \]

Dejando

\[k z=\sin \dfrac{\theta}{2} \text { and } k=\sin \dfrac{\theta_{0}}{2}\nonumber \]

la ecuación diferencial se convierte

\[\dfrac{d z}{d \tau}=\pm \omega \sqrt{1-z^{2}} \sqrt{1-k^{2} z^{2}}\nonumber \]

Aplicando la separación de variables, encontramos

\[\pm \omega\left(t-t_{0}\right) =\dfrac{1}{\omega} \int_{1}^{z} \dfrac{d z}{\sqrt{1-z^{2}} \sqrt{1-k^{2} z^{2}}} \nonumber \]

\[=\int_{0}^{1} \dfrac{d z}{\sqrt{1-z^{2}} \sqrt{1-k^{2} z^{2}}}-\int_{0}^{z} \dfrac{d z}{\sqrt{1-z^{2}} \sqrt{1-k^{2} z^{2}}} \nonumber \]

\[=K(k)-F\left(\sin ^{-1}\left(k^{-1} \sin \theta\right), k\right) \nonumber \]

La solución,\(\theta(t)\), se encuentra entonces resolviendo para\(z\) y usando\(k z=\sin \dfrac{\theta}{2}\) para resolver para\(\theta\). Esto requiere que sepamos invertir la integral elíptica,\(F(z, k)\).

Las funciones elípticas son el resultado de la inversión de integrales elípticas. Considerar

\[u(\sin \phi, k) =F(\phi, k) =\int_{0}^{\phi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}} \nonumber \]

\[=\int_{0}^{\sin \phi} \dfrac{d t}{\sqrt{\left(1-t^{2}\right)\left(1-k^{2} t^{2}\right)}} \nonumber \]

Nota:\(F(\phi, 0)=\phi\) y\(F(\phi, 1)=\ln (\sec \phi+\tan \phi)\). En estos casos\(F\) es obviamente monótona cada vez mayor y por lo tanto debe haber una inversa.

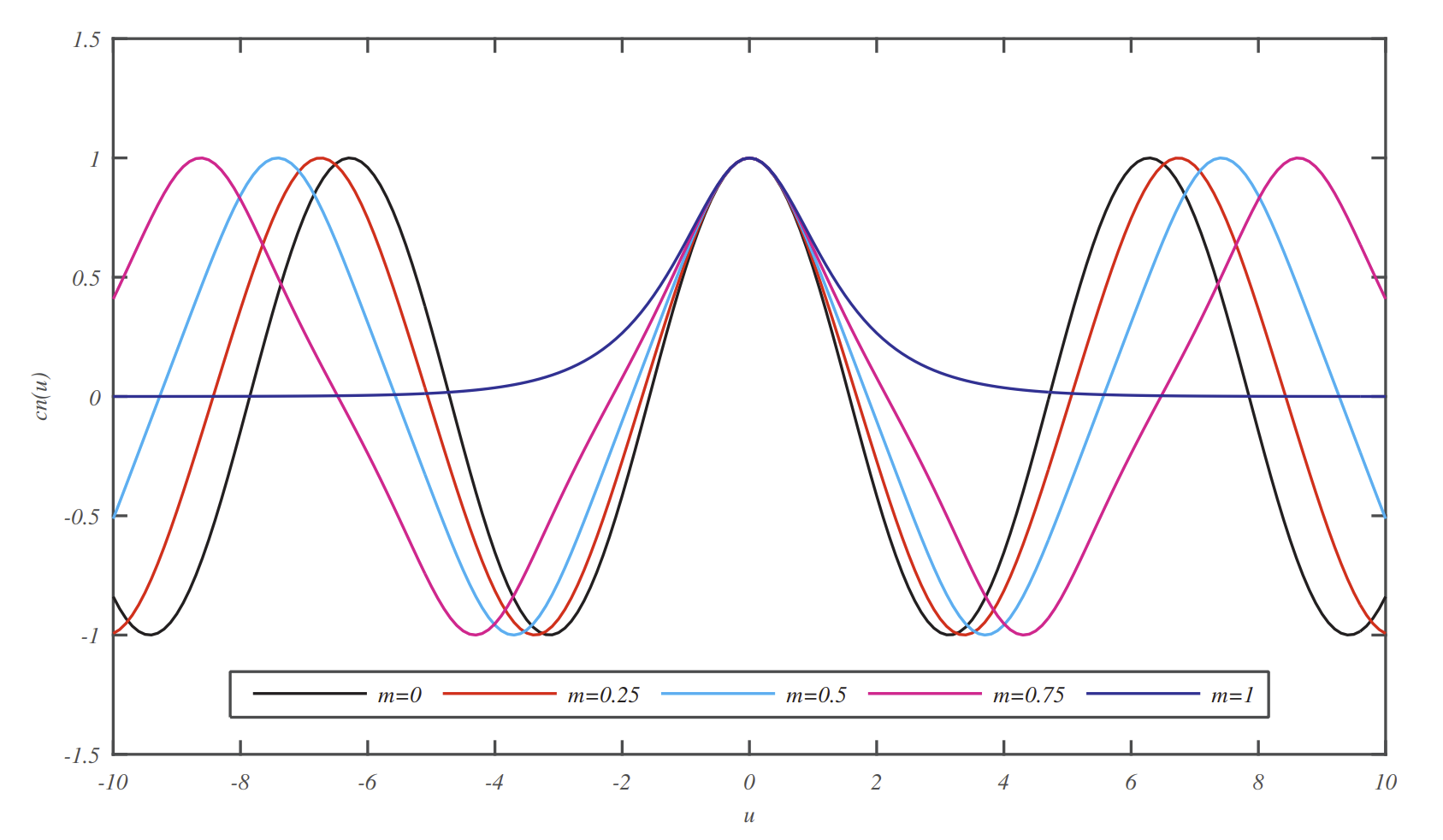
El inverso de Ecuación\(\PageIndex{1}\) se define como\(\phi=F^{-1}(u, k)=\operatorname{am}(u, k)\), donde\(u=\sin \phi\). La función\(\operatorname{am}(u, k)\) se llama la función de amplitud Jacobi y\(k\) es el módulo elíptico. [En algunas referencias y software como los paquetes MATLAB,\(m=k^{2}\) se utiliza como parámetro.] Tres de las funciones elípticas de Jacobi, mostradas en la Figura\(\PageIndex{1}\), se pueden definir en términos de la función de amplitud mediante

\[\begin{aligned} &\operatorname{sn}(u, k)=\sin \operatorname{am}(u, k)=\sin \phi, \\ &\operatorname{cn}(u, k)=\cos \operatorname{am}(u, k)=\cos \phi, \end{aligned} \nonumber \]

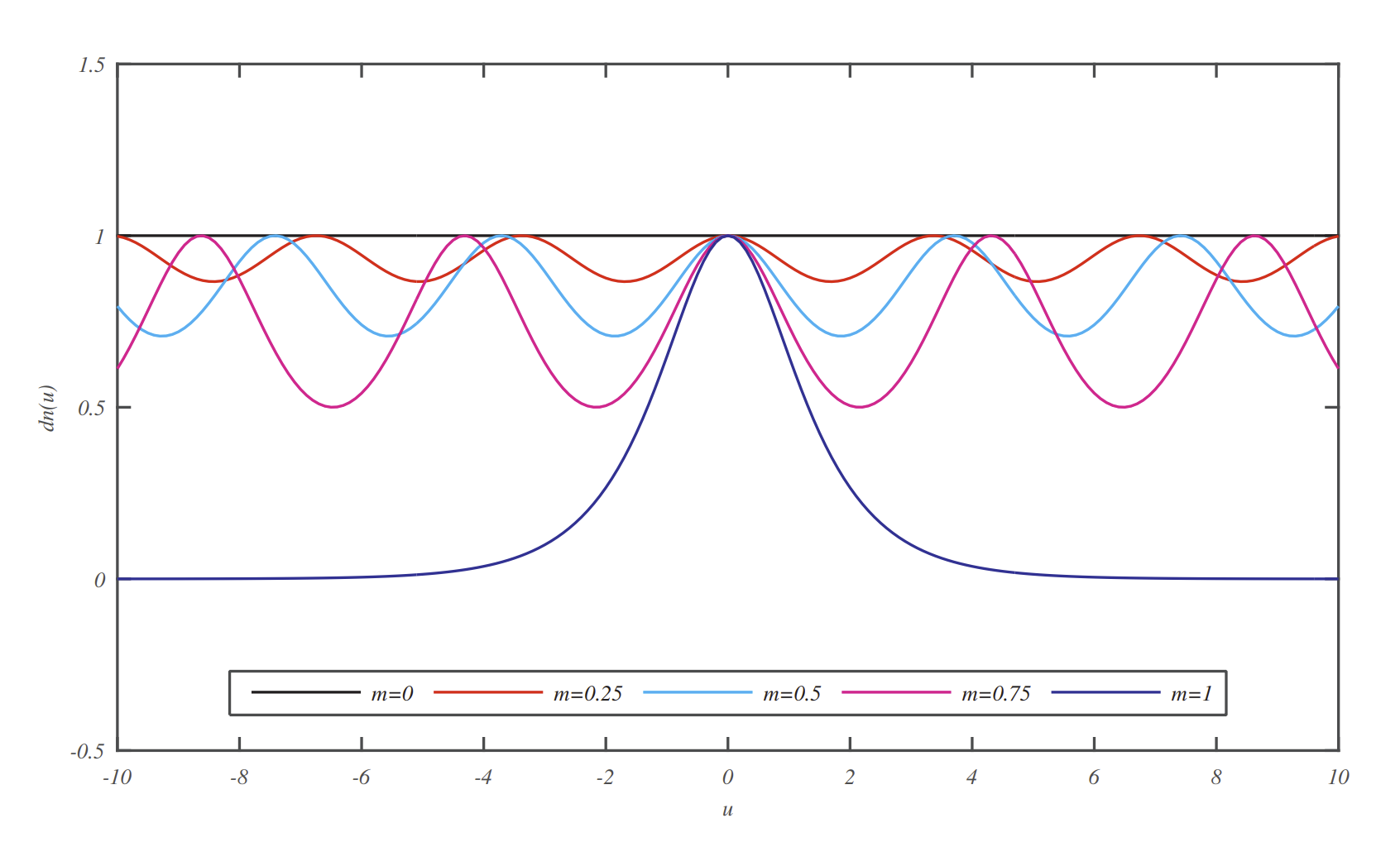
y la amplitud delta

(Funciones elípticas Jacobi).

\[\operatorname{dn}(u, k)=\sqrt{1-k^{2} \sin ^{2} \phi}\nonumber. \nonumber \]

Se relacionan a través de las identidades

\[\mathrm{cn}^{2}(u, k)+\mathrm{sn}^{2}(u, k)=1 \nonumber \]

\[\mathrm{dn}^{2}(u, k)+k^{2} \operatorname{sn}^{2}(u, k)=1 \nonumber \]

Figura\(\PageIndex{1}\): Gráficas de las funciones elípticas Jacobi\(\operatorname{sn}(u, k), \operatorname{cn}(u, k)\), y\(\operatorname{dn}(u, k)\)
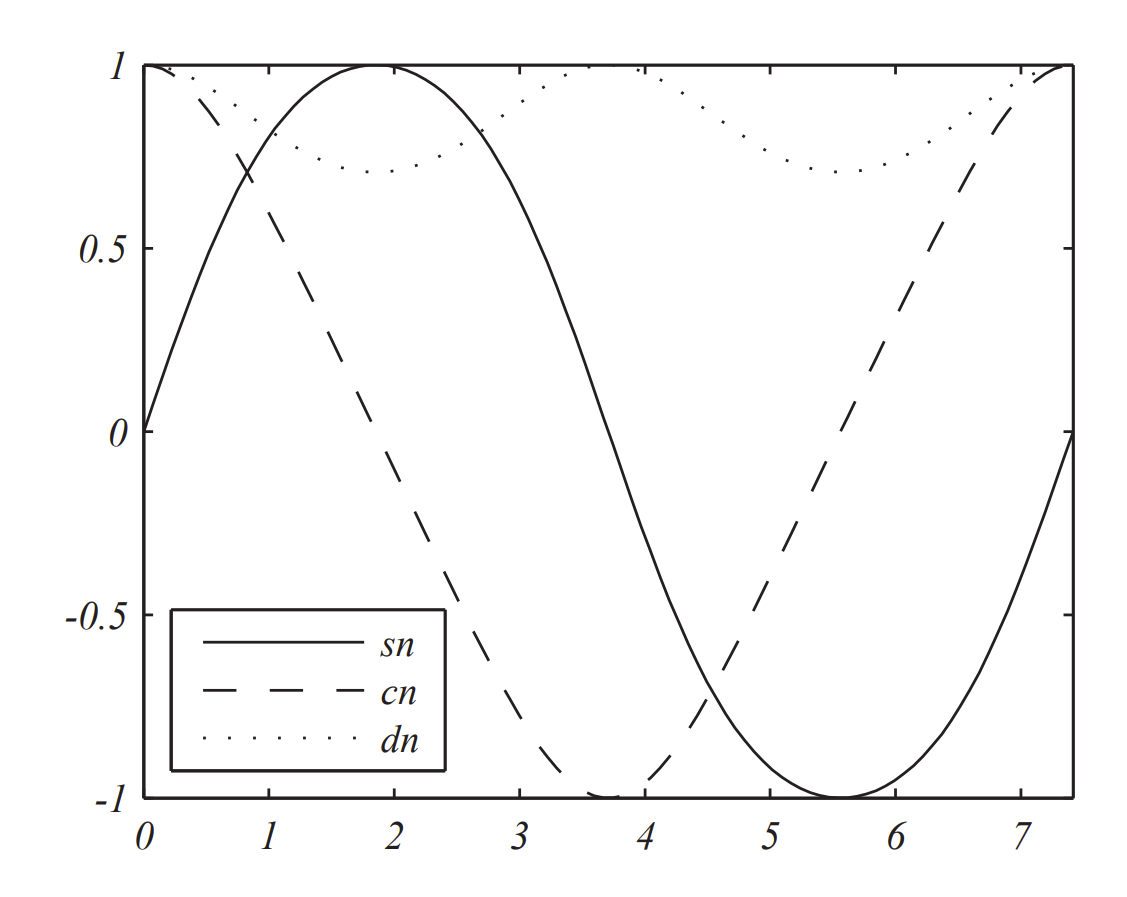
para\(m=k^{2}=0.5\). Aquí\(K(k)=1.8541\)

Las funciones elípticas se pueden extender al plano complejo. En este caso las funciones son doblemente periódicas. No obstante, no necesitaremos considerarlo en el texto actual.

También, vemos que estas funciones son periódicas. El periodo se da en renta texto. términos de la integral elíptica completa del primer tipo,\(K(k)\). Considerar

\[ \begin{aligned} F(\phi+2 \pi, k) &=\int_{0}^{\phi+2 \pi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}} \\ &=\int_{0}^{\phi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}}+\int_{\phi}^{\phi+2 \pi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}} \\ &=F(\phi, k)+\int_{0}^{2 \pi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}} \\ &=F(\phi, k)+4 K(k) \end{aligned} \label{7.86} \]

Desde entonces\(F(\phi+2\pi , k) = u +4K\), tenemos

\[\operatorname{sn}(u + 4K) = \sin(\operatorname{am}(u + 4K)) = \sin(\operatorname{am}(u) + 2\pi) = \sin \operatorname{am}(u) = \operatorname{sn} u \nonumber \]

En general, tenemos

\[\operatorname{sn}(u+2 K, k) =-\operatorname{sn}(u, k) \nonumber \]

\[\operatorname{cn}(u+2 K, k) =-\operatorname{cn}(u, k) \nonumber \]

\[\operatorname{dn}(u+2 K, k) =\operatorname{dn}(u, k) \nonumber \]

Las gráficas de\(\operatorname{sn}(u)\),\(\operatorname{cn}(u)\), y\(\operatorname{dn}(u)\), se muestran en las Figuras\(\PageIndex{2}\) -\(\PageIndex{4}\).

Figura\(\PageIndex{2}\): Gráficas de\(\mathrm{sn}(u, k)\)
\(0,0.25,0.50,0.75,1.00\).

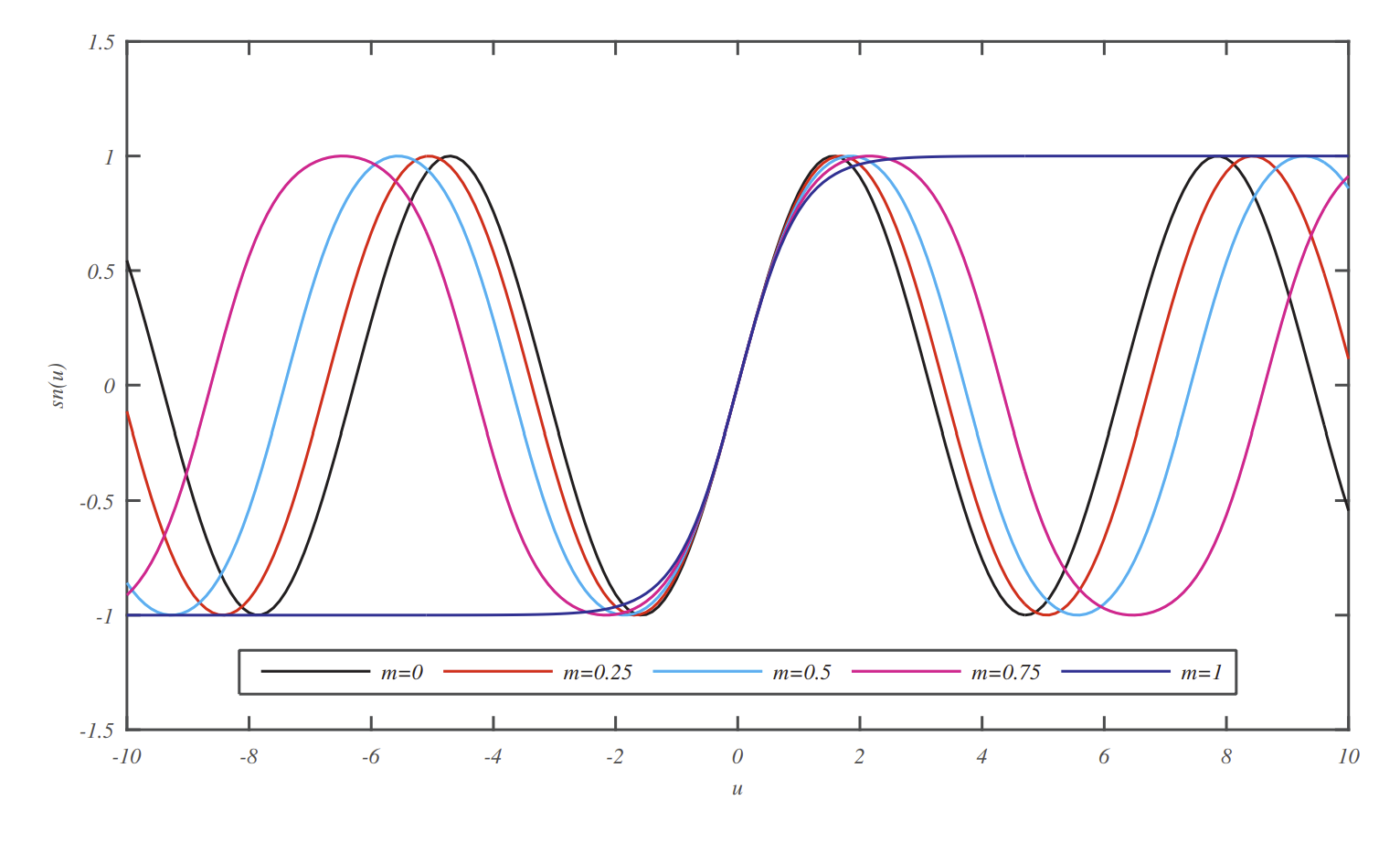
Figura\(\PageIndex{3}\): Gráficas de\(\mathrm{cn}(u, k)\) para\(m=\)\(0,0.25,0.50,0.75,1.00\).

A saber,

\[\begin{gathered} \operatorname{sn}(u+K, k)=\dfrac{\operatorname{cn} u}{\operatorname{dn} u}, \quad \operatorname{sn}(u+2 K, k)=-\operatorname{sn} u, \\ \operatorname{cn}(u+K, k)=-\sqrt{1-k^{2} \dfrac{\operatorname{sn} u}{\operatorname{dn} u}}, \quad \operatorname{dn}(u+2 K, k)=-\operatorname{cn} u, \end{gathered} \nonumber \]

Figura\(\PageIndex{4}\): Gráficas de dn\((u, k)\) para\(m=0,0.25,0.50,0.75,1.00\)

\[\operatorname{dn}(u+K, k)=\dfrac{\sqrt{1-k^{2}}}{\operatorname{dn} u}, \quad \operatorname{dn}(u+2 K, k)=\mathrm{dn} u. \nonumber \]

Por lo tanto, dn y cn tienen un periodo de\(4 K\) y dn tiene un periodo de\(2 K\).

Los valores especiales que se encuentran en la Figura\(\PageIndex{1}\) se ven como

\[\begin{gathered} \operatorname{sn}(K, k)=1 \\ \operatorname{cn}(K, k)=0 \\ \operatorname{dn}(K, k)=\sqrt{1-k^{2}}=k^{\prime} \end{gathered} \nonumber \]

donde\(k^{\prime}\) se llama el módulo complementario.

Importantes para esta sección son las derivadas de estas funciones elípticas,

\[\begin{gathered} \dfrac{\partial}{\partial u} \operatorname{sn}(u, k)=\operatorname{cn}(u, k) \operatorname{dn}(u, k) \\ \dfrac{\partial}{\partial u} \operatorname{cn}(u, k)=-\operatorname{sn}(u, k) \operatorname{dn}(u, k) \\ \dfrac{\partial}{\partial u} \operatorname{dn}(u, k)=-k^{2} \operatorname{sn}(u, k) \operatorname{cn}(u, k) \end{gathered} \nonumber \]

y la función de amplitud

\[\dfrac{\partial}{\partial u} \operatorname{am}(u, k)=\operatorname{dn}(u, k) \nonumber \]

A veces las funciones elípticas Jacobi se muestran sin referencia al módulo elíptico, como\(\operatorname{sn}(u)=\operatorname{sn}(u, k)\). Cuando\(k\) se entiende, podemos hacer lo mismo.

Ejemplo\(\PageIndex{1}\)

Mostrar que\(\operatorname{sn}(u)\) satisface la ecuación diferencial

\[y^{\prime \prime}+\left(1+k^{2}\right) y=2 k^{2} y^{3} \nonumber \]

De los derivados anteriores, tenemos que

\[ \begin{aligned} \dfrac{d^{2}}{d u^{2}} \operatorname{sn}(u) &=\dfrac{d}{d u}(\operatorname{cn}(u) \operatorname{dn}(u)) \\ &=-\operatorname{sn}(u) \operatorname{dn}^{2}(u)-k^{2} \operatorname{sn}(u) \operatorname{cn}^{2}(u) \end{aligned} \label{7.90} \]

Dejar\(y(u)=\operatorname{sn}(u)\) y usar las identidades\(\PageIndex{9}- \PageIndex{10}\), tenemos eso

\[y^{\prime \prime}=-y\left(1-k^{2} y^{2}\right)-k^{2} y\left(1-y^{2}\right)=-\left(1+k^{2}\right) y+2 k^{2} y^{3} \nonumber \]

Este es el resultado deseado.

Ejemplo\(\PageIndex{2}\)

Demostrar que\(\theta(t)=2 \sin ^{-1}(k \operatorname{sn} t)\) es una solución de la ecuación\(\ddot{\theta}+\sin \theta=0\).

Diferenciando\(\theta(t)=2 \sin ^{-1}(k \operatorname{sn} t)\), tenemos

\[ \begin{aligned} \dfrac{d^{2}}{d t^{2}}\left(2 \sin ^{-1}(k \operatorname{sn} t)\right) &=\dfrac{d}{d t}\left(2 \dfrac{k \operatorname{cn} t \operatorname{dn} t}{\sqrt{1-k^{2} \operatorname{sn}^{2} t}}\right) \\ &=\dfrac{d}{d t}(2 k \operatorname{cn} t) \\ &=-2 k \operatorname{sn} t \operatorname{dn} t \end{aligned} \label{7.91} \]

Sin embargo, podemos evaluar\(\sin \theta\) para un rango de\(\theta\). Por lo tanto, tenemos

\[ \begin{aligned} \sin \theta &=\sin \left(2 \sin ^{-1}(k \operatorname{sn} t)\right) \\ &=2 \sin \left(\sin ^{-1}(k \operatorname{sn} t)\right) \cos \left(\sin ^{-1}(k \operatorname{sn} t)\right) \\ &=2 k \operatorname{sn} t \sqrt{1-k^{2} \operatorname{sn}^{2} t} \\ &=2 k \operatorname{sn} t \operatorname{dn} t \end{aligned} \label{7.92} \]

Comparando estos resultados, lo hemos demostrado\(\ddot{\theta}+\sin \theta=0\).

La solución al último ejemplo se puede utilizar para obtener la solución exacta al problema del péndulo no lineal,\(\ddot{\theta}+\omega^{2} \sin \theta=0, \theta(0)=\theta_{0}, \dot{\theta}(0)=0\). La solución general viene dada por\(\theta(t)=2 \sin ^{-1}(k \operatorname{sn}(\omega t+\phi))\) donde se\(\phi\) tiene que determinar a partir de las condiciones iniciales. Tomamos nota de que

\[\begin{aligned} \dfrac{d \operatorname{sn}(u+K)}{d u} &=\operatorname{cn}(u+K) \operatorname{dn}(u+K) \\ &=\left(-\sqrt{1-k^{2}} \dfrac{\operatorname{sn} u}{\operatorname{dn} u}\right)\left(\dfrac{\sqrt{1-k^{2}}}{\operatorname{dn} u}\right) \\ &=-\left(1-k^{2}\right) \dfrac{\operatorname{sn} u}{\operatorname{dn}^{2} u} \end{aligned} \label{7.93} \]

Evaluando en\(u=0\), tenemos\(\operatorname{sn}^{\prime}(K)=0 .\)

Por lo tanto, si elegimos\(\phi=K\), entonces\(\dot{\theta}(0)=0\) y la solución es

\[\theta(t)=2 \sin ^{-1}(k \operatorname{sn}(\omega t+K)) \nonumber \]

Además, se encuentra que el otro valor inicial es

\[\theta(0)=2 \sin ^{-1}(k \operatorname{sn} K)=2 \sin ^{-1} k \nonumber \]

Así,\(k=\sin \dfrac{\theta_{0}}{2}\), como habíamos visto en la derivación anterior de la solución integral elíptica. La solución se da como

\[\theta(t)=2 \sin ^{-1}\left(\sin \dfrac{\theta_{0}}{2} \operatorname{sn}(\omega t+K)\right) \nonumber \]

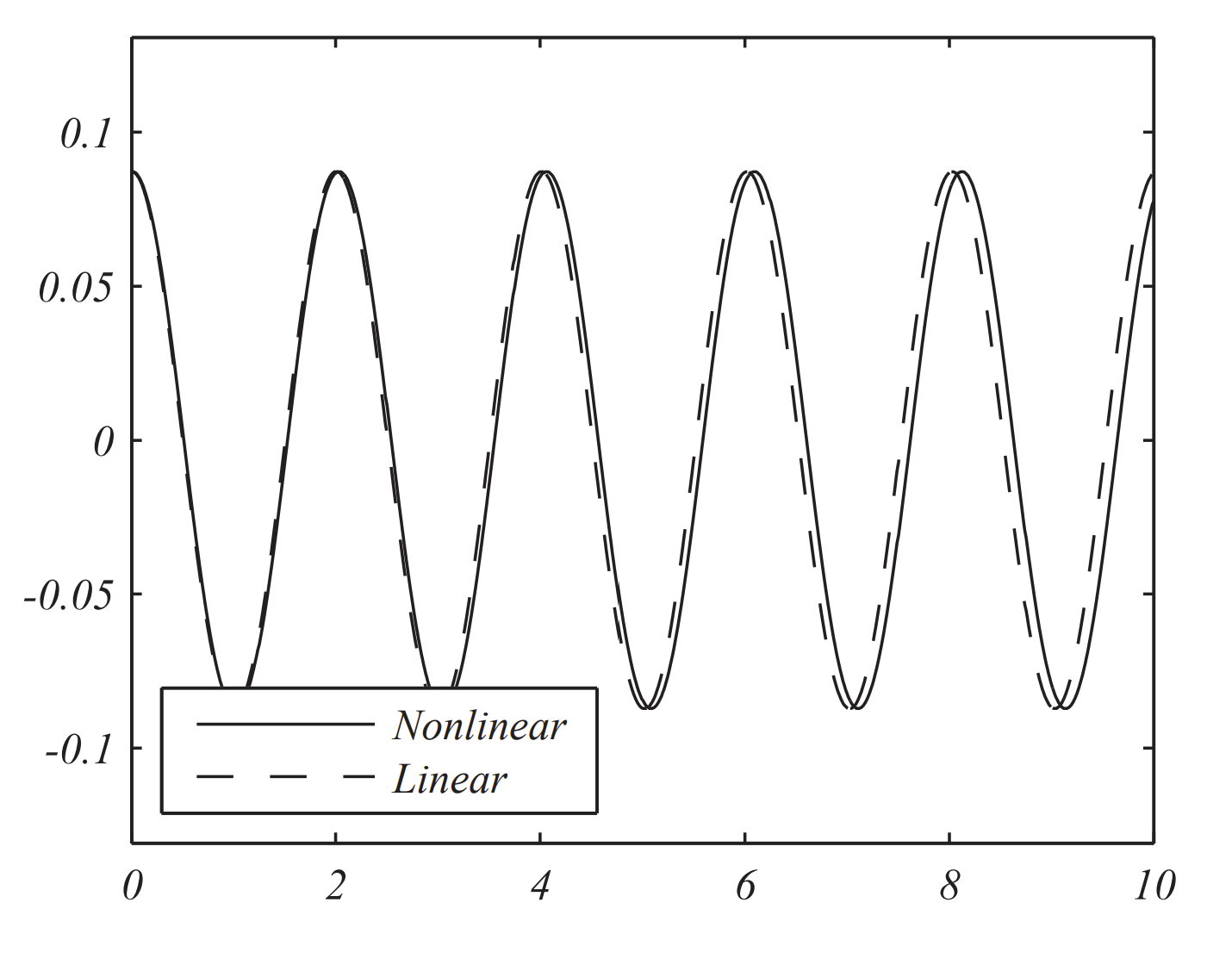
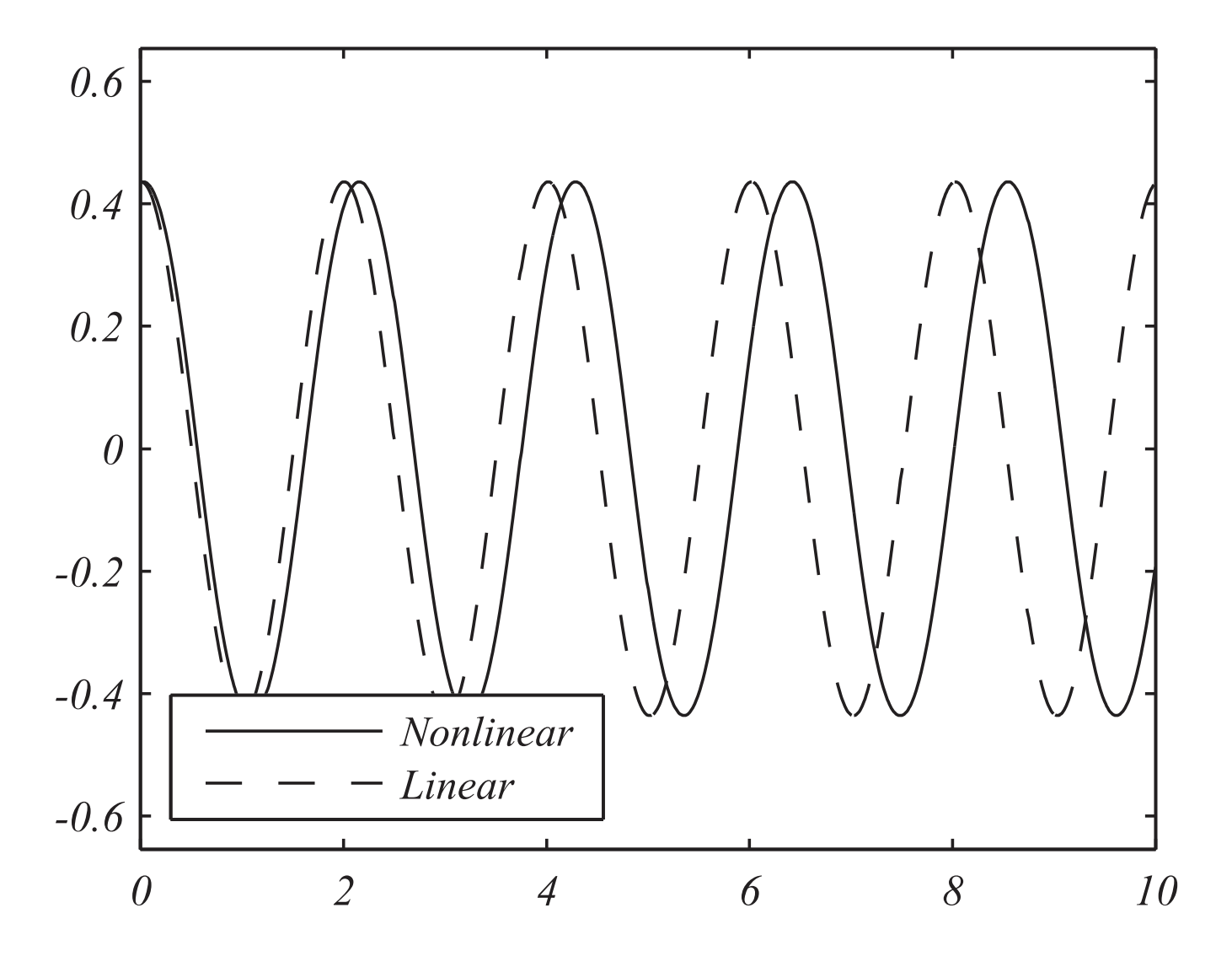
En las Figuras\(\PageIndex{5} - \PageIndex{6}\), se muestran comparaciones de las soluciones exactas de los problemas de péndulo lineal y no lineal para los ángulos iniciales\(L=1.0 \mathrm{~m}\)\(\theta_{0}=10^{\circ}\) y\(\theta_{0}=50^{\circ} .\)

Figura\(\PageIndex{5}\): Comparación de soluciones exactas de los problemas de péndulo lineal y no lineal para\(L=1.0 \mathrm{~m}\) y\(\theta_{0}=10^{\circ}\).

Figura\(\PageIndex{6}\): Comparación de las soluciones exactas de los problemas de péndulo lineal y no lineal para\(L=1.0 \mathrm{~m}\) y\(\theta_{0}=50^{\circ}\).