8.3: Funciones hiperbólicas
- Page ID
- 119757
Entonces, ¿hay alguna otra función que sea útil en física? En realidad, hay muchos más. No obstante, probablemente no hayas visto muchos de ellos hasta la fecha. Veremos al final del semestre que hay muchas funciones importantes que surgen como soluciones de algunos problemas de física bastante genéricos, pero importantes. En tus clases de cálculo también has visto que algunas relaciones están representadas en forma paramétrica. No obstante, hay al menos otro conjunto de funciones elementales, que ya deberías conocer. Estas son las funciones hiperbólicas. Tales funciones son útiles para representar cables colgantes, órbitas no delimitadas y ondas viajeras especiales llamadas solitones. También juegan un papel en la relatividad especial y general.
Los solitones son soluciones especiales para algunas ecuaciones genéricas de ondas no lineales. Por lo general, experimentan colisiones elásticas y desempeñan papeles especiales en una variedad de campos de la física, como la hidrodinámica y la óptica. Una solución simple de soliton es de la forma
\[u(x, t)=2 \eta^{2} \operatorname{sech}^{2} \eta\left(x-4 \eta^{2} t\right)\nonumber \]
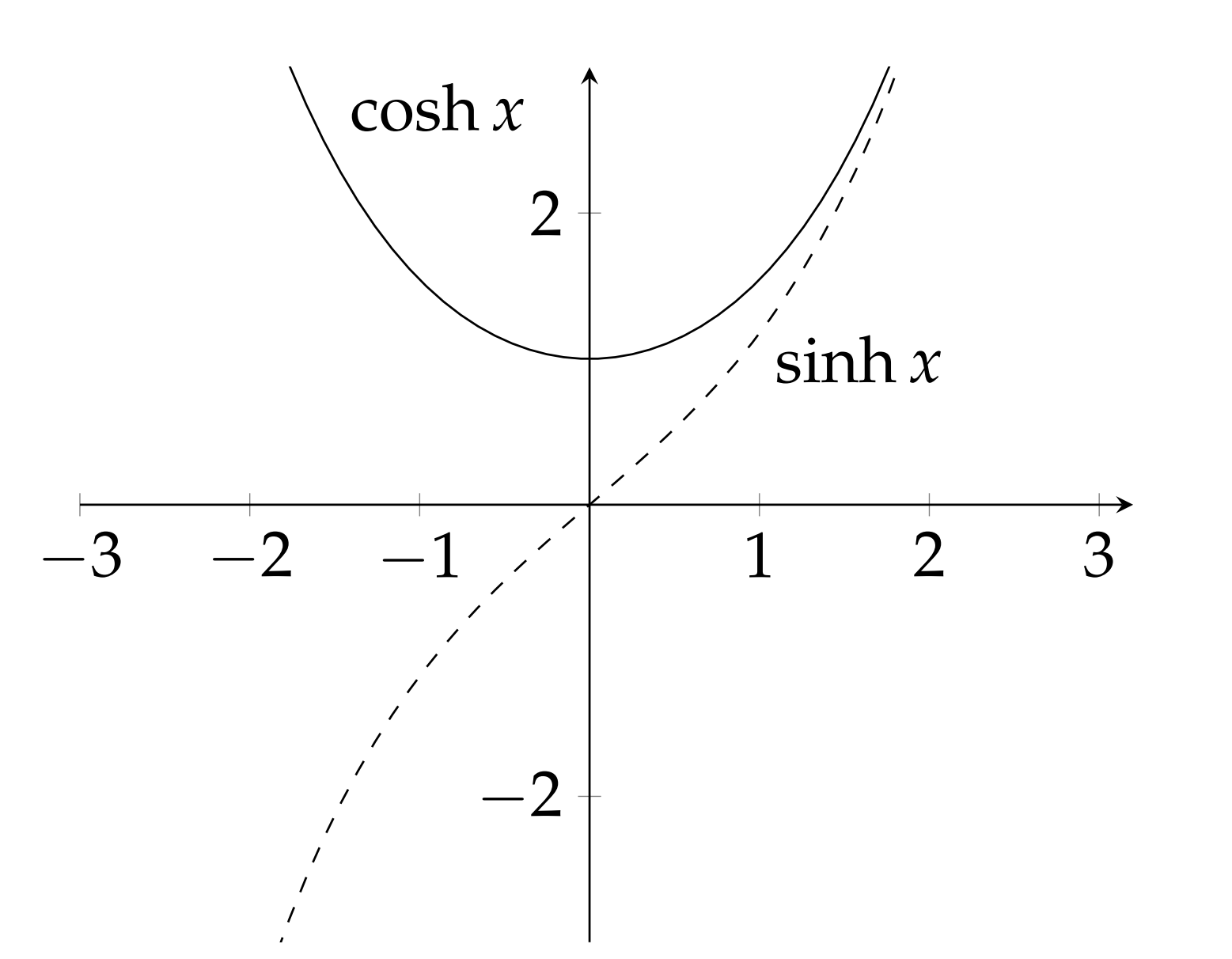
(Funciones hiperbólicas). Recordamos algunas definiciones e identidades de funciones hiperbólicas: el seno hiperbólico y el coseno hiperbólico (mostrados en la Figura\(\PageIndex{1}\)):
\[\sinh x =\dfrac{e^{x}-e^{-x}}{2} \nonumber \]
\[\cosh x =\dfrac{e^{x}+e^{-x}}{2} \nonumber \]
Las funciones hiperbólicas están relacionadas con las funciones trigonométricas. Esto lo podemos ver desde las relaciones
\[\begin{aligned} \sin \theta &=\dfrac{e^{i \theta}-e^{-i \theta}}{2 i} \\ \cos \theta &=\dfrac{e^{i \theta}+e^{-i \theta}}{2} \end{aligned} \nonumber \]
Dejando\(\theta=i x\) que tengamos\(\sin i x=i \sinh x\) y\(\cos i x=\cosh x .\)
Hay otras cuatro funciones hiperbólicas. Estas se definen en términos de las funciones anteriores similares a las relaciones entre las funciones trigonométricas. Es decir, así como todas las funciones trigonométricas se pueden construir desde el seno y el coseno, las funciones hiperbólicas se pueden definir en términos del seno hiperbólico y el coseno hiperbólico. Tenemos
\[ \tanh x =\dfrac{\sinh x}{\cosh x}=\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \nonumber \]
\[ \operatorname{sech} x =\dfrac{1}{\cosh x}=\dfrac{2}{e^{x}+e^{-x}} \nonumber \]
\[ \operatorname{csch} x =\dfrac{1}{\sinh x}=\dfrac{2}{e^{x}-e^{-x}} \nonumber \]
\[ \operatorname{coth} x =\dfrac{1}{\tanh x}=\dfrac{e^{x}+e^{-x}}{e^{x}-e^{-x}} \nonumber \]
También hay todo un conjunto de identidades, similares a las de las funciones trigonométricas. Por ejemplo, la identidad pitagórica para funciones trigonométricas,\(\sin ^{2} \theta+\cos ^{2} \theta=1\), se sustituye por la identidad
\[\cosh ^{2} x-\sinh ^{2} x=1 \nonumber \]
Esto se muestra fácilmente simplemente usando las definiciones de estas funciones. Esta identidad también es útil para proporcionar un conjunto paramétrico de ecuaciones que describen las hiperbolas. Dejando\(x=a \cosh t\) y\(y=b \sinh t\), uno tiene
\[\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=\cosh ^{2} t-\sinh ^{2} t=1 \nonumber \]
(Identidades hiperbólicas). Una lista de identidades de funciones hiperbólicas que se necesitan comúnmente son dadas por lo siguiente:
\[\cosh ^{2} x-\sinh ^{2} x =1, \nonumber \]
\[\tanh ^{2} x+\operatorname{sech}^{2} x =1, \nonumber \]
\[\cosh (A \pm B) =\cosh A \cosh B \pm \sinh A \sinh B, \nonumber \]
\[\sinh (A \pm B) =\sinh A \cosh B \pm \sinh B \cosh A, \nonumber \]
\[\cosh 2 x =\cosh ^{2} x+\sinh ^{2} x, \nonumber \]
\[\sinh 2 x =2 \sinh ^{2} \cosh x, \nonumber \]
\[\cosh ^{2} x =\dfrac{1}{2}(1+\cosh 2 x), \nonumber \]
\[\sinh ^{2} x =\dfrac{1}{2}(\cosh 2 x-1) \nonumber \]
Obsérvese la similitud con las identidades trigonométricas. De éstas se pueden derivar otras identidades.
También existen funciones hiperbólicas inversas y éstas pueden escribirse en términos de logaritmos. Al igual que con las funciones trigonométricas inversas, comenzamos con la definición
\[y=\sinh ^{-1} x \quad \Leftrightarrow \quad x=\sinh y . \nonumber \]
El objetivo es escribir\(y\) en términos de\(x\) sin utilizar la función inversa. En primer lugar, observamos que
\[x=\dfrac{1}{2}\left(e^{y}-e^{-y}\right) . \nonumber \]
A continuación resolvemos para\(e^{y}\). Esto se hace señalando eso\(e^{-y}=\dfrac{1}{e^{y}}\) y reescribiendo la ecuación anterior como
\[0=\left(e^{y}\right)^{2}-2 x e^{y}-1 \nonumber \]
Esta ecuación está en forma cuadrática que podemos resolver usando la fórmula cuadrática como
\[e^{y}=x+\sqrt{1+x^{2}} \nonumber \]
(Sólo hay una raíz ya que esperamos que el exponencial sea positivo.)
El último paso es resolver para\(y\),
\[y=\ln \left(x+\sqrt{1+x^{2}}\right) \nonumber \]
Las funciones hiperbólicas inversas atendidas por\(\sinh ^{-1} x=\ln \left(x+\sqrt{1+x^{2}}\right)\),\(\cosh ^{-1} x=\ln \left(x+\sqrt{x^{2}-1}\right)\),\(\tanh ^{-1} x=\dfrac{1}{2} \ln \dfrac{1+x}{1-x}\).


