8.7: Serie Power
- Page ID
- 119786
OTRO EJEMPLO DE UNA SERIE INFINITA que el alumno ha encontrado en cursos anteriores es la serie power. Ejemplos de tales series son proporcionados por las series Taylor y Maclaurin.
Una expansión de la serie de potencia sobre\(x=a\) con la secuencia de coeficientes\(c_{n}\) viene dada por\(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\). Por ahora consideraremos que todas las constantes son números reales con\(x\) en algún subconjunto del conjunto de números reales.
Considera la siguiente expansión sobre\(x=0\):
\[\sum_{n=0}^{\infty} x^{n}=1+x+x^{2}+\ldots \nonumber \]
Nos gustaría darle sentido a tales expansiones. ¿Para qué valores de\(x\) convergerá esta serie infinita? Hasta ahora no prestábamos mucha atención a qué series infinitas podrían converger. No obstante, esta serie en particular ya nos resulta familiar. Se trata de una serie geométrica. Obsérvese que cada término se obtiene del anterior a través de la multiplicación por\(r=x\). El primer término es\(a=1 .\) Así, a partir de la Ecuación 8.6.5, tenemos que la suma de la serie viene dada por
\[\sum_{n=0}^{\infty} x^{n}=\dfrac{1}{1-x}, \quad|x|<1\nonumber \]
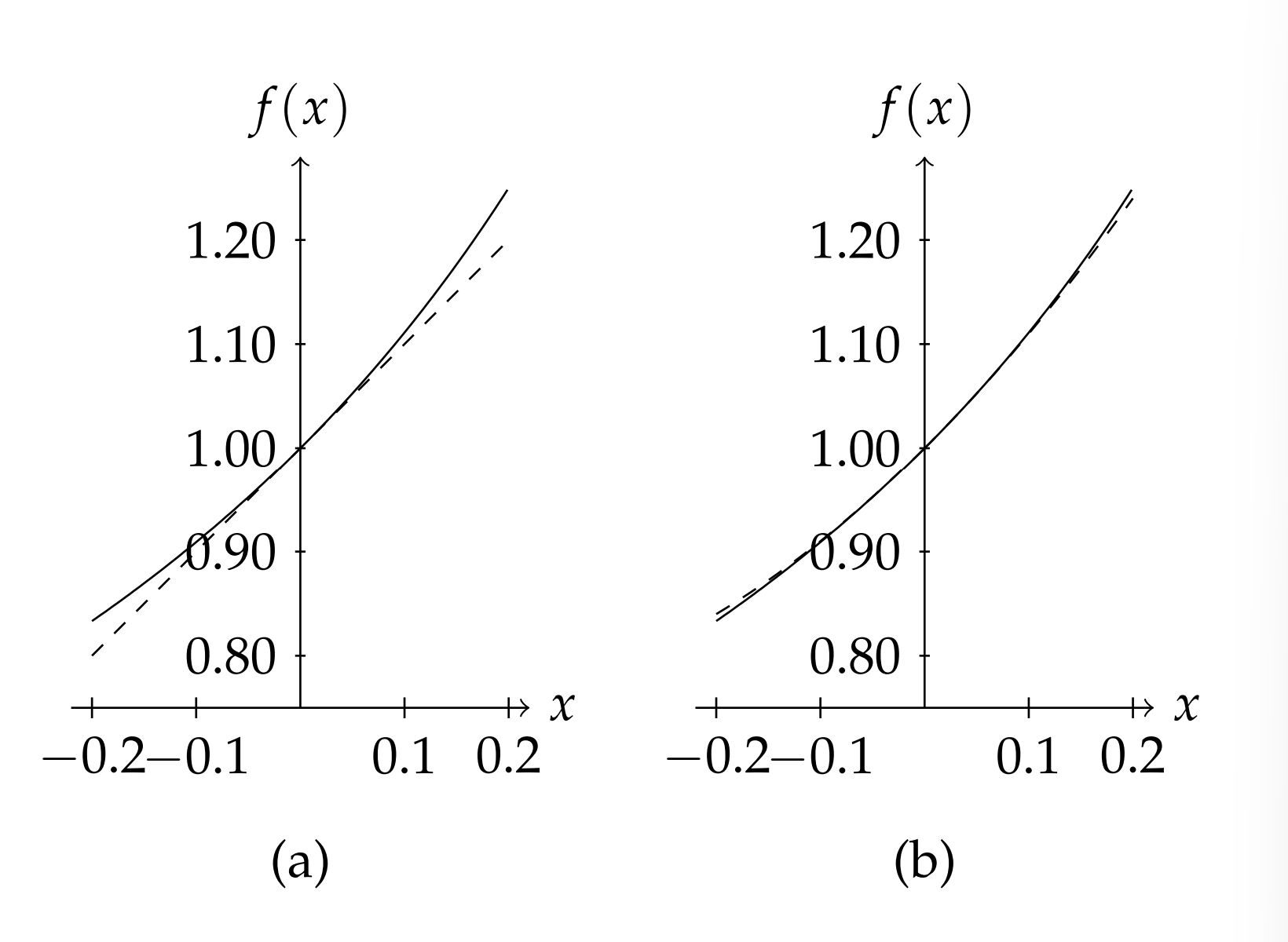
En este caso vemos que la suma, cuando existe, es una función sencilla. De hecho, cuando\(x\) es pequeño, podemos usar esta serie infinita para proporcionar aproximaciones a la función\((1-x)^{-1}\). Si\(x\) es lo suficientemente pequeño, podemos escribir
\[(1-x)^{-1} \approx 1+x \nonumber \]
\(1+x+x^{2}\) (punteado) y\(1+x+x^{2}+x^{3}\)
En la Figura\(\PageIndex{1}\) a vemos que para valores pequeños de\(x\) estas funciones sí están de acuerdo. (punteado) para\(x \in[-1.0,0.7]\).
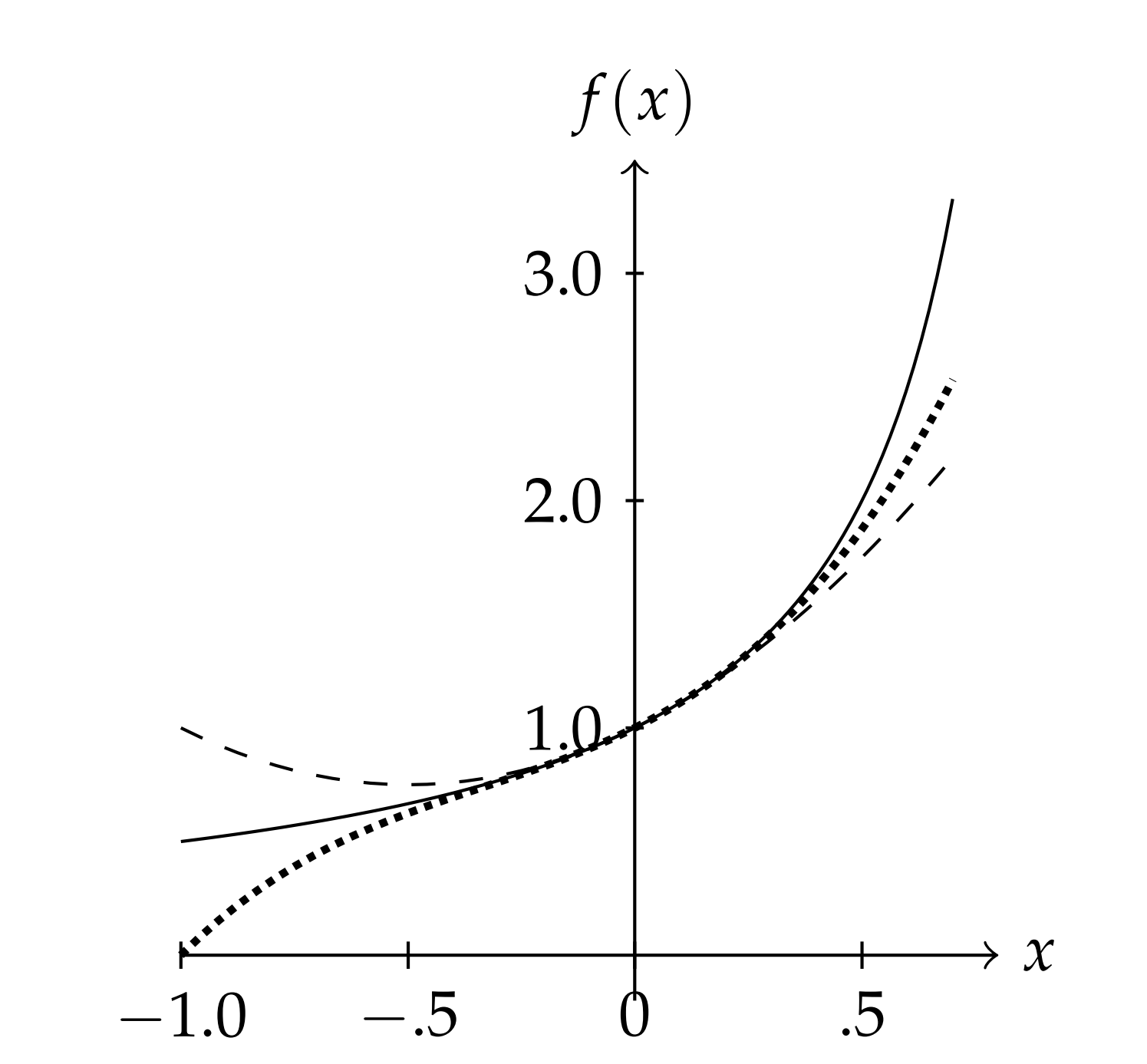
Por supuesto, si queremos un mejor acuerdo, seleccionamos más términos. En la Figura\(\PageIndex{1}\) b vemos lo que sucede cuando lo hacemos. El acuerdo es mucho mejor. Pero extendiendo el intervalo, vemos en Figura\(\PageIndex{2}\) que mantener sólo términos cuadráticos puede no ser lo suficientemente bueno. Mantener los términos cúbicos da un mejor acuerdo a lo largo del intervalo.
Finalmente, en la Figura\(\PageIndex{3}\) se muestra la suma de los primeros 21 términos a lo largo de todo el intervalo\([-1,1]\). Tenga en cuenta que hay problemas con aproximaciones cercanas a los puntos finales del intervalo,\(x=\pm 1\).
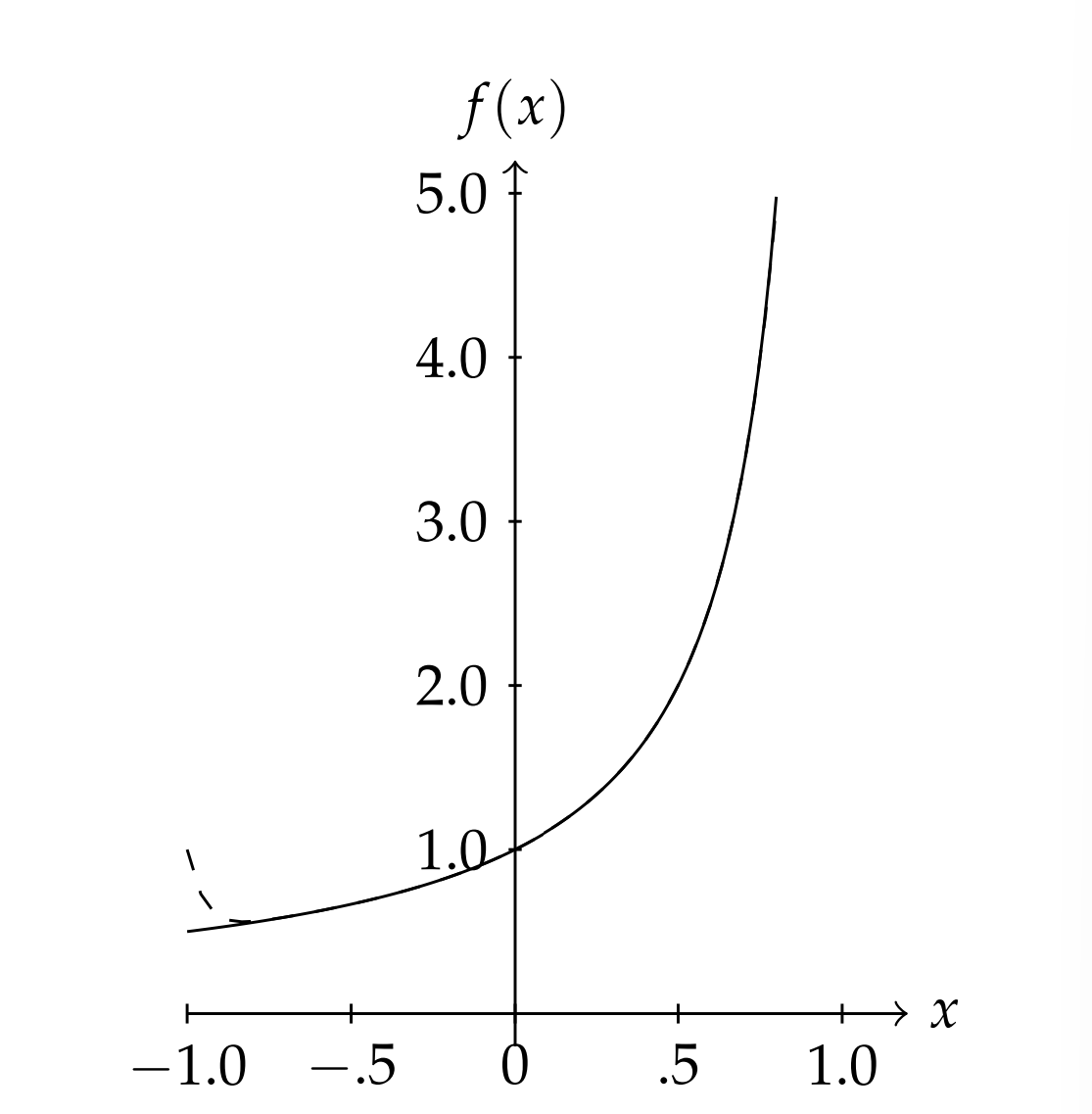
Tales aproximaciones polinómicas se denominan polinomios de Taylor. Así,\(T_{3}(x)=1+x+x^{2}+x^{3}\) es la aproximación polinomio Taylor de tercer orden de\(f(x)=\dfrac{1}{1-x}\).
Con este ejemplo hemos visto lo útil que puede ser una representación en serie para una función dada. No obstante, la representación en serie era una serie geométrica simple, que ya sabíamos sumar. ¿Hay alguna manera de comenzar con una función y luego encontrar su representación en serie? Una vez que tengamos tal representación, ¿convergerá la serie a la función con la que empezamos? ¿Para qué valores de\(x\) convergerá? Estas preguntas pueden ser respondidas recordando las definiciones de las series Taylor y Maclaurin.
Una expansión de la serie Taylor de\(f(x)\) aproximadamente\(x=a\) es la serie
\[f(x) \sim \sum_{n=0}^{\infty} c_{n}(x-a)^{n} \nonumber \]
donde
\[c_{n}=\dfrac{f^{(n)}(a)}{n !} \nonumber \]
Tenga en cuenta que usamos ∼ para indicar que aún tenemos que determinar cuándo la serie puede converger a la función dada. Una clase especial de series son aquellas series de Taylor para las que se trata la expansión\(x=0 .\) Estas se llaman serie Maclaurin.
Expansión de la serie Maclaurin.
Una expansión de la serie Maclaurin de\(f(x)\) es una expansión de la serie Taylor de\((x)\) aproximadamente\(x=0\), o
\[f(x) \sim \sum_{n=0}^{\infty} c_{n}(x)^{n} \nonumber \]
donde
\[c_{n}=\dfrac{f^{(n)}(0)}{n !} \text {. } \nonumber \]
Ampliar\(f(x)=e^{x}\) sobre\(x=0\).
Solución
Comenzamos por crear una mesa. Para poder calcular los coeficientes de expansión\(c_{n}\),, necesitaremos realizar diferenciaciones repetidas de\(f(x) .\) So, proporcionamos una tabla para estas derivadas. Entonces, solo necesitamos evaluar la segunda columna en\(x=0\) y dividirla por\(n !\).
| \(n\) | \(f^{(n)}(x)\) | \(f^{(n)}(0)\) | \(c_{n}\) |
|---|---|---|---|
| \ (n\)” style="text-align:center;” class="lt-math-91104">0 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(e^{x}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(e^{0}=1\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{0 !}=1\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">1 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(e^{x}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(e^{0}=1\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{1 !}=1\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">2 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(e^{x}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(e^{0}=1\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{2 !}\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">3 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(e^{x}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(e^{0}=1\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{3 !}\) |
A continuación, miramos la última columna e intentamos determinar un patrón para que podamos anotar el término general de la serie. Si solo hay una necesidad de obtener una aproximación polinómica, entonces los primeros términos pueden ser suficientes. En este caso, el patrón es obvio:\(c_{n}=\dfrac{1}{n !} .\) Entonces,
\[e^{x} \sim \sum_{n=0}^{\infty} \dfrac{x^{n}}{n !} \nonumber \]
Ampliar\(f(x)=e^{x}\) sobre\(x=1\).
Solución
Aquí buscamos una expansión de la forma\(e^{x} \sim \sum_{n=0}^{\infty} c_{n}(x-1)^{n} .\) Podríamos crear una tabla como el último ejemplo. De hecho, la última columna tendría valores de la forma\(\dfrac{e}{n !}\). (Debe confirmar esto.) Sin embargo, haremos uso de la expansión de la serie Maclaurin\(e^{x}\) y obtendremos el resultado más rápido. Tenga en cuenta que\(e^{x}=e^{x-1+1}=e e^{x-1}\). Ahora, aplique la expansión conocida para\(e^{x}\):
\(e^{x} \sim e\left(1+(x-1)+\dfrac{(x-1)^{2}}{2}+\dfrac{(x-1)^{3}}{3 !}+\ldots\right)=\sum_{n=0}^{\infty} \dfrac{e(x-1)^{n}}{n !}\)
Ampliar\(f(x)=\dfrac{1}{1-x}\) sobre\(x=0\).
Solución
Este es el ejemplo con el que iniciamos nuestra discusión. Podemos configurar una tabla para encontrar los coeficientes de la serie Maclaurin. Vemos de la última columna de la tabla que recuperamos la serie geométrica Ecuación\(\PageIndex{1}\).
| \(n\) | \(f^{(n)}(x)\) | \(f^{(n)}(0)\) | \(c_{n}\) |
|---|---|---|---|
| \ (n\)” style="text-align:center;” class="lt-math-91104">0 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{1-x}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">1 | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{0 !}=1\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">1 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{(1-x)^{2}}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">1 | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{1}{1 !}=1\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">2 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{2(1)}{(1-x)^{3}}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(2(1)\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{2 !}{2 !}=1\) |
| \ (n\)” style="text-align:center;” class="lt-math-91104">3 | \ (f^ {(n)} (x)\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{3(2)(1)}{(1-x)^{4}}\) | \ (f^ {(n)} (0)\)” style="text-align:center;” class="lt-math-91104">\(3(2)(1)\) | \ (c_ {n}\)” style="text-align:center;” class="lt-math-91104">\(\dfrac{3 !}{3 !}=1\) |
Entonces, hemos encontrado
\[\dfrac{1}{1-x} \sim \sum_{n=0}^{\infty} x^{n} \nonumber \]
Podemos reemplazar\(\sim\) por igualdad si podemos determinar el rango de\(x\) -valores para el cual converge la serie infinita resultante. En breve investigaremos dicha convergencia.
Las expansiones en serie para muchas funciones elementales surgen en una variedad de aplicaciones. Algunas expansiones comunes se proporcionan en la Figura\(\PageIndex{4}\).

Todavía necesitamos determinar los valores\(x\) para los cuales converge una serie de potencias dada. Las primeras cinco de las expansiones anteriores convergen para todos los reales, pero las otras sólo convergen para\(|x|<1\).
Consideramos la convergencia de\(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\). Para\(x=a\) la serie obviamente converge. ¿Convergerá para otros puntos? Uno puede probar
Si\(\sum_{n=0}^{\infty} c_{n}(b-a)^{n}\) converge para\(b \neq a\), entonces\(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\) converge absolutamente para todos\(x\) satisfactorios\(|x-a|<|b-a| .\)
Esto lleva a tres posibilidades
- \(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\)sólo puede converger en\(x=a\).
- \(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\)pueden converger para todos los números reales.
- \(\sum_{n=0}^{\infty} c_{n}(x-a)^{n}\)converge para\(|x-a|<R\) y diverge para\(\mid x-\)\(a \mid>R\).
(Intervalo y radio de convergencia). El número\(R\) se llama el radio de convergencia de la serie de potencia y\((a-R, a+R)\) se llama el intervalo de convergencia. La convergencia en los puntos finales de este intervalo tiene que ser probada para cada serie de potencia.
Para determinar el intervalo de convergencia, solo hay que señalar que cuando una serie de potencias converge, lo hace absolutamente. Entonces, sólo necesitamos probar la convergencia de\(\sum_{n=0}^{\infty}\left|c_{n}(x-a)^{n}\right|=\sum_{n=0}^{\infty}\left|c_{n}\right||x-a|^{n}\). Esto se hace fácilmente usando la prueba de relación o la prueba de raíz\(n\) th. Primero identificamos los términos\(a_{n}=\left|c_{n}\right||x-a|^{n}\) no negativos y luego aplicamos una de las pruebas de convergencia del plan de estudios de cálculo.
Por ejemplo, la\(n\) Prueba Raíz da la condición de convergencia para\(a_{n}=\)\(\left|c_{n}\right||x-a|^{n}\),
\[\rho=\lim _{n \rightarrow \infty} \sqrt[n]{a_{n}}=\lim _{n \rightarrow \infty} \sqrt[n]{\left|c_{n}\right| \mid x}-a \mid<1 \nonumber \]
Dado que\(|x-a|\) es independiente de\(n_{\prime}\), podemos factorizarlo fuera del límite y dividir el valor del límite para obtener
\[|x-a|<\left(\lim _{n \rightarrow \infty} \sqrt[n]{\left|c_{n}\right|}\right)^{-1} \equiv R\nonumber \]
Así, hemos encontrado el radio de convergencia,\(R\).
De igual manera, podemos aplicar la Prueba de Ratio.
\[\rho=\lim _{n \rightarrow \infty} \dfrac{a_{n+1}}{a_{n}}=\lim _{n \rightarrow \infty} \dfrac{\left|c_{n+1}\right|}{\left|c_{n}\right|}|x-a|<1 \nonumber \]
Nuevamente, reescribimos este resultado para determinar el radio de convergencia:
\[|x-a|<\left(\lim _{n \rightarrow \infty} \dfrac{\left|c_{n+1}\right|}{\left|c_{n}\right|}\right)^{-1} \equiv R\nonumber \]
Encuentra el radio de convergencia de la serie\(e^{x}=\sum_{n=0}^{\infty} \dfrac{x^{n}}{n !}\).
Solución
Ya que hay un factorial, utilizaremos la Prueba de Ratio.
\[\rho=\lim _{n \rightarrow \infty} \dfrac{|n !|}{|(n+1) !|}|x|=\lim _{n \rightarrow \infty} \dfrac{1}{n+1}|x|=0 \nonumber \]
Ya que\(\rho=0\), es independiente de\(|x|\) y así la serie converge para todos También\(x .\) podemos decir que el radio de convergencia es infinito.
Encuentra el radio de convergencia de la serie\(\dfrac{1}{1-x}=\)\(\sum_{n=0}^{\infty} x^{n} .\)
Solución
En este ejemplo usaremos el\(n\) th Root Test.
\[\rho=\lim _{n \rightarrow \infty} \sqrt[n]{1}|x|=|x|<1. \nonumber \]
Así, encontramos que tenemos convergencia absoluta para\(|x|<1\). Ajuste\(x=1\) o\(x=-1\), encontramos que las series resultantes no convergen. Entonces, los puntos finales no están incluidos en el intervalo completo de convergencia.
En este ejemplo también podríamos haber utilizado la Prueba de Ratio. Por lo tanto,
\[\rho=\lim _{n \rightarrow \infty} \dfrac{1}{1}|x|=|x|<1.\nonumber \]
Hemos obtenido el mismo resultado que cuando usamos el\(n\) th Root Test.
Encuentra el radio de convergencia de la serie\(\sum_{n=1}^{\infty} \dfrac{3^{n}(x-2)^{n}}{n}\).
Solución
En este ejemplo, tenemos una expansión sobre\(x=2\). Usando el\(n\) th
Root Test encontramos que
\[\rho=\lim _{n \rightarrow \infty} \sqrt[n]{\dfrac{3^{n}}{n}}|x-2|=3|x-2|<1 .\nonumber \]
Resolviendo por\(|x-2|\) en esta desigualdad, nos encontramos\(|x-2|<\dfrac{1}{3}\). Así, el radio de convergencia es\(R=\dfrac{1}{3}\) y el intervalo de convergencia es\(\left(2-\dfrac{1}{3}, 2+\dfrac{1}{3}\right)=\left(\dfrac{5}{3}, \dfrac{7}{3}\right)\).
En cuanto a los puntos finales, primero probamos el punto\(x=\dfrac{7}{3}\). La serie resultante es\(\sum_{n=1}^{\infty} \dfrac{3^{n}\left(\dfrac{1}{3}\right)^{n}}{n}=\sum_{n=1}^{\infty} \dfrac{1}{n}\). Esta es la serie armónica, y así no converge. Insertando\(x=\dfrac{5}{3}\), obtenemos la serie armónica alterna. Esta serie sí converge. Entonces, tenemos convergencia encendida\(\left[\dfrac{5}{3}, \dfrac{7}{3}\right)\). Sin embargo, solo es condicionalmente convergente en el punto final izquierdo,\(x= \dfrac{5}{3}\).
Encuentra una expansión de\(f(x)=\dfrac{1}{x+2}\) aproximadamente\(x=1\).
Solución
En lugar de computar explícitamente la expansión de la serie Taylor para esta función, podemos hacer uso de una función ya conocida. Primero escribimos\(f(x)\) en función de\(x-1\), ya que estamos expandiendo sobre\(x=1\); es decir, estamos buscando una serie cuyos términos sean poderes de\(x-1\).
Esta expansión se realiza fácilmente al señalar que\(\dfrac{1}{x+2}=\dfrac{1}{(x-1)+3} .\) Factorizando un 3, podemos reescribir esta expresión como una suma de una serie geométrica. A saber, utilizamos la expansión para
\[ \begin{aligned} g(z) &=\dfrac{1}{1+z} \\ &=1-z+z^{2}-z^{3}+\ldots \end{aligned} \label{A.101} \]
y luego reescribimos\(f(x)\) como
\[ \begin{aligned} f(x) &=\dfrac{1}{x+2} \\ &=\dfrac{1}{(x-1)+3} \\ &=\dfrac{1}{3\left[1+\dfrac{1}{3}(x-1)\right]} \end{aligned} \nonumber \]
\[=\dfrac{1}{3} \dfrac{1}{1+\dfrac{1}{3}(x-1)} \nonumber \]
Tenga en cuenta que\(f(x)=\dfrac{1}{3} g\left(\dfrac{1}{3}(x-1)\right)\) para\(g(z)=\dfrac{1}{1+z} .\) So, la expansión se convierte
\[f(x)=\dfrac{1}{3}\left[1-\dfrac{1}{3}(x-1)+\left(\dfrac{1}{3}(x-1)\right)^{2}-\left(\dfrac{1}{3}(x-1)\right)^{3}+\ldots\right] \nonumber \]
Esto se puede simplificar aún más como
\[f(x)=\dfrac{1}{3}-\dfrac{1}{9}(x-1)+\dfrac{1}{27}(x-1)^{2}-\ldots \nonumber \]
La convergencia se establece fácilmente. La expansión para\(g(z)\) converge para\(|z|<1 .\) So, la expansión para\(f(x)\) converge para\(\left|-\dfrac{1}{3}(x-1)\right|<\) 1. Esto implica que\(|x-1|<3\). Poniendo esta desigualdad en notación de intervalos, tenemos que la serie power converge absolutamente para\(x \in\)\((-2,4)\). Al insertar los puntos finales, se puede mostrar que la serie diverge para ambos\(x=-2\) y\(x=4\). ¡Deberías verificar esto!
Probar la fórmula de Euler:\(e^{i \theta}=\cos \theta+i \sin \theta\).
Solución
La Fórmula de Euler\(e^{i \theta}=\cos \theta+i \sin \theta\),, es una fórmula importante y se utiliza en todo el texto.
Como aplicación final, podemos derivar la Fórmula de Euler,
\[e^{i \theta}=\cos \theta+i \sin \theta \nonumber \]
donde\(i=\sqrt{-1}\). Usamos ingenuamente la expansión para\(e^{x}\) con\(x=i \theta\). Esto nos lleva a
\[e^{i \theta}=1+i \theta+\dfrac{(i \theta)^{2}}{2 !}+\dfrac{(i \theta)^{3}}{3 !}+\dfrac{(i \theta)^{4}}{4 !}+\ldots \nonumber \]
A continuación señalamos que cada término tiene un poder de\(i\). La secuencia de poderes de\(i\) se da como\(\{1, i,-1,-i, 1, i,-1,-i, 1, i,-1,-i, \ldots\} .\) Ver el patrón? Concluimos que
\[i^{n}=i^{r}, \text { where } r=\text { remainder after dividing } n \text { by } 4 \nonumber \]
Esto da
\[e^{i \theta}=\left(1-\dfrac{\theta^{2}}{2 !}+\dfrac{\theta^{4}}{4 !}-\ldots\right)+i\left(\theta-\dfrac{\theta^{3}}{3 !}+\dfrac{\theta^{5}}{5 !}-\ldots\right) \nonumber \]
Reconocemos las expansiones entre paréntesis como las de las funciones coseno y seno. Así, terminamos con la Fórmula de Euler.
A partir de este resultado derivamos relaciones, que serán importantes para nuestros próximos estudios. De la fórmula de Euler tenemos eso para entero\(n\):
\[e^{i n \theta}=\cos (n \theta)+i \sin (n \theta)\nonumber \]
También contamos con
\[e^{i n \theta}=\left(e^{i \theta}\right)^{n}=(\cos \theta+i \sin \theta)^{n} \nonumber \]
Igualando estas dos expresiones, nos llevan a la Fórmula de Moivre, que lleva el nombre de Abraham de Moivre\((1667-1754)\),
\[(\cos \theta+i \sin \theta)^{n}=\cos (n \theta)+i \sin (n \theta) \nonumber \]
Esta fórmula es útil para derivar identidades relacionando poderes de senos o cosenos con funciones simples. Por ejemplo, si tomamos\(n=2\) en Ecuación\(\PageIndex{8}\), encontramos
\[\cos 2 \theta+i \sin 2 \theta=(\cos \theta+i \sin \theta)^{2}=\cos ^{2} \theta-\sin ^{2} \theta+2 i \sin \theta \cos \theta \nonumber \]
Mirar las partes reales e imaginarias de este resultado conduce a las conocidas identidades de doble ángulo
\[\cos 2 \theta=\cos ^{2} \theta-\sin ^{2} \theta, \quad \sin 2 \theta=2 \sin \theta \cos \theta \nonumber \]
Fórmulas:
\[\cos 2 \theta=\cos ^{2} \theta-\sin ^{2} \theta, \quad \sin 2 \theta=2 \sin \theta \cos \theta \nonumber \]
Sustitución\(\cos^2 \theta = 1 − \sin^2 \theta\) o\(\sin^2 \theta = 1 − \cos^2 \theta \) conduce a las fórmulas de medio ángulo:
\[\cos ^{2} \theta=\dfrac{1}{2}(1+\cos 2 \theta), \quad \sin ^{2} \theta=\dfrac{1}{2}(1-\cos 2 \theta) \nonumber \]
También podemos usar la Fórmula de Euler para escribir senos y cosenos en términos de exponenciales complejos. Primero notamos que debido a que el coseno es una función par y el seno es una función impar, tenemos
\[e^{-i \theta}=\cos \theta-i \sin \theta \nonumber \]
Combinando esto con la Fórmula de Euler, tenemos que
\[\cos \theta=\dfrac{e^{i \theta}+e^{-i \theta}}{2}, \quad \sin \theta=\dfrac{e^{i \theta}-e^{-i \theta}}{2 i} \nonumber \]
Finalmente observamos que existe una relación simple entre las funciones hiperbólicas y las funciones trigonométricas. Recordemos que
\[\cosh x=\dfrac{e^{x}+e^{-x}}{2} \nonumber \]
Si lo dejamos\(x = i\theta\), entonces tenemos eso\(\cosh(i\theta) = \cos \theta \) y\(\cos(ix) = \cosh x\). Del mismo modo, podemos demostrarlo\(\sinh(i\theta) = i sin \theta \) y\(\sin(ix) = −i \sinh x\)
Aquí vemos elegantes pruebas de identidades trigonométricas bien conocidas.
\[\cos 2 \theta=\cos ^{2} \theta-\sin ^{2} \theta \nonumber \]
\[\begin{aligned} &\sin 2 \theta=2 \sin \theta \cos \theta \\ & \cos ^{2} \theta=\dfrac{1}{2}(1+\cos 2 \theta) \\ & \sin ^{2} \theta=\dfrac{1}{2}(1+\cos 2 \theta) \\ & \sin ^{2} \theta=\dfrac{1}{2}(1-\cos 2 \theta) \text {. } \end{aligned} \nonumber \]
Las funciones trigonométricas se pueden escribir en términos de exponenciales complejos:
\[\begin{aligned} &\cos \theta=\dfrac{e^{i \theta}+e^{-i \theta}}{2} \\ &\sin \theta=\dfrac{e^{i \theta}-e^{-i \theta}}{2 i} \end{aligned} \nonumber \]
Las funciones hiperbólicas y trigonométricas están íntimamente relacionadas.
\[\begin{gathered} \cos (i x)=\cosh x, \\ \sin (i x)=-i \sinh x . \end{gathered} \nonumber \]


