8.3: Propiedades de las funciones de Green

Hemos anotado algunas propiedades de las funciones de Green en la última sección. En esta sección vamos a elaborar algunas de estas propiedades como una herramienta para construir rápidamente las funciones de Green para problemas de valor límite. Aquí hay una lista de las propiedades basadas en nuestra solución anterior.

Propiedades de la Función de los Verdes

1. Ecuación Diferencial:

\(\dfrac{\partial}{\partial x}\left(p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right)+q(x) G(x, \xi)=0, x \neq \xi\)

Porque\(x<\xi\) estamos en la segunda rama y\(G(x, \xi)\) es proporcional a\(y_{1}(x)\). Así, ya que\(y_{1}(x)\) es una solución de la ecuación homogénea, entonces así es\(G(x, \xi)\). Porque\(x>\xi\) estamos en la primera rama y\(G(x, \xi)\) es proporcional a\(y_{2}(x)\). Entonces, una vez más\(G(x, \xi)\) es una solución del problema homogéneo.

2. Condiciones de Límite:

Porque\(x=a\) estamos en la segunda rama y\(G(x, \xi)\) es proporcional a\(y_{1}(x)\). Así, cualquiera que sea la condición\(y_{1}(x)\) que satisfaga,\(G(x, \xi)\) satisfará. Se puede hacer una declaración similar para\(x=b\).

3. Simetría o Reciprocidad:\(G(x, \xi)=G(\xi, x)\)

Esto lo habíamos mostrado en la última sección.

4. Continuidad de\(\mathbf{G}\) en\(x=\xi\):\(G\left(\xi^{+}, \xi\right)=G\left(\xi^{-}, \xi\right)\)

Aquí hemos definido

\ begin {alineado}
&G\ izquierda (\ xi^ {+}, x\ derecha) =\ lim _ {x\ flecha abajo\ xi} G (x,\ xi),\ quad x>\ xi\
&G\ izquierda (\ xi^ {-}, x\ derecha) =\ lim _ {x\ uparrow\ xi} G (x,\ xi),\ quad x<\ xi
\ fin {alineado}

\(x=\xi\)Ambientando en ambas ramas, tenemos

\[\dfrac{y_{1}(\xi) y_{2}(\xi)}{p W}=\dfrac{y_{1}(\xi) y_{2}(\xi)}{p W} \nonumber \]

5. Discontinuidad de salto de\(\dfrac{\partial G}{\partial x}\) al\(x=\xi\):

\[\dfrac{\partial G\left(\xi^{+}, \xi\right)}{\partial x}-\dfrac{\partial G\left(\xi^{-}, \xi\right)}{\partial x}=\dfrac{1}{p(\xi)} \nonumber \]

Este caso no es tan obvio. Primero calculamos las derivadas anotando qué rama está involucrada y luego evaluamos las derivadas y las restamos. Así, tenemos

\ [\ begin {alineado}
\ dfrac {\ parcial G\ izquierda (\ xi^ {+},\ xi\ derecha)} {\ parcial x} -\ dfrac {\ parcial G\ izquierda (\ xi^ {-},\ xi\ derecha)} {\ parcial x} &=-\ dfrac {1} {p W^ {\ prime}} y_ {1} (\ xi) y_ {2} ^ {\ prime} (\ xi) +\ dfrac {1} {p W} y_ {1} ^ {\ prime} (\ xi) y_ {2} (\ xi)\\
&=-\ dfrac {y_ {1} ^ {\ prime} (\ xi) y_ {2} (\ xi ) -y_ {1} (\ xi) y_ {2} ^ {\ prime} (\ xi)} {p (\ xi)\ left (y_ {1} (\ xi) y_ {2} ^ {\ prime} (\ xi) -y_ {1} ^ {\ prime} (\ xi) y_ {2} (\ xi)\ xi)\ derecha)}\\
&=\ dfrac {1} {p (\ xi)}
\ final {alineado}\ etiqueta {8.47}\]

Ahora mostramos cómo el conocimiento de estas propiedades permite construir rápidamente una función de Green.

Ejemplo 8.5. Construir la función del Verde para el problema

\ begin {reunió}
y^ {\ prime\ prime} +\ omega^ {2} y=f (x),\ quad 0<x<1,\\
y (0) =0=y (1),
\ end {reunidos}

con\(\omega \neq 0\).

I. Encontrar soluciones a la ecuación homogénea.

Una solución general a la ecuación homogénea se da como

\[y_{h}(x)=c_{1} \sin \omega x+c_{2} \cos \omega x . \nonumber \]

Así pues, para\(x \neq \xi\),

\[G(x, \xi)=c_{1}(\xi) \sin \omega x+c_{2}(\xi) \cos \omega x \nonumber \]

II. Condiciones de Límite.

Primero, tenemos\(G(0, \xi)=0\) para\(0 \leq x \leq \xi\). Entonces,

\[G(0, \xi)=c_{2}(\xi) \cos \omega x=0 \nonumber \]

Entonces,

\[G(x, \xi)=c_{1}(\xi) \sin \omega x, \quad 0 \leq x \leq \xi . \nonumber \]

Segundo, tenemos\(G(1, \xi)=0\) para\(\xi \leq x \leq 1\). Entonces,

\[G(1, \xi)=c_{1}(\xi) \sin \omega+c_{2}(\xi) \cos \omega .=0 \nonumber \]

Se puede elegir una solución con

\[c_{2}(\xi)=-c_{1}(\xi) \tan \omega \nonumber \]

Esto da

\[G(x, \xi)=c_{1}(\xi) \sin \omega x-c_{1}(\xi) \tan \omega \cos \omega x . \nonumber \]

Esto puede simplificarse factorizando los términos restantes\(c_{1}(\xi)\) y colocando los términos restantes sobre un denominador común. El resultado es

\ [\ begin {alineado}
G (x,\ xi) &=\ dfrac {c_ {1} (\ xi)} {\ cos\ omega} [\ sin\ omega x\ cos\ omega-\ sin\ omega\ cos\ omega x]\\
&=-\ dfrac {c_ {1} (\ xi)} {\ cos\ omega}\ sin omega (1-x)
\ fin {alineado}\ etiqueta {8.48}\]

Dado que el coeficiente es arbitrario en este punto, ya que se puede escribir el resultado como

\[G(x, \xi)=d_{1}(\xi) \sin \omega(1-x), \quad \xi \leq x \leq 1 \nonumber \]

Observamos que podríamos haber comenzado\(y_{2}(x)=\sin \omega(1-x)\) como una de nuestras soluciones linealmente independientes del problema homogéneo en anticipación que\(y_{2}(x)\) satisface la segunda condición límite.

III. Simetría o Reciprocidad

Ahora lo imponemos\(G(x, \xi)=G(\xi, x)\). A este punto tenemos que

\ (G (x,\ xi) =\ left\ {\ begin {array} {cc}
c_ {1} (\ xi)\ sin\ omega x, & 0\ leq x\ leq\ xi\\
d_ {1} (\ xi)\ sin\ omega (1-x), &\ xi\ leq x\ leq 1
\ end {array}. \ derecho.\)

Podemos hacer que las ramas sean simétricas escogiendo las formas adecuadas para\(c_{1}(\xi)\) y\(d_{1}(\xi)\). Nosotros elegimos\(c_{1}(\xi)=C \sin \omega(1-\xi)\) y\(d_{1}(\xi)=C \sin \omega \xi .\) Entonces,

\ (G (x,\ xi) =\ izquierda\ {\ comenzar {matriz} {l}
C\ sin\ omega (1-\ xi)\ sin\ omega x, 0\ leq x\ leq\ xi\\
C\ sin\ omega (1-x)\ sin\ omega\ xi,\ xi\ leq x\ leq 1
\ end {array}. \ derecho.\)

Ahora la función del Verde es simétrica y aún tenemos que determinar la constante\(C\). Observamos que podríamos haber llegado a este punto usando el Método de Variación de Parámetros resultado donde\(C=\dfrac{1}{p W}\).

IV. Continuidad de\(G(x, \xi)\)

Observamos que ya tenemos continuidad en virtud de la simetría impuesta en el último paso.

V. Salto Discontinuidad en\(\dfrac{\partial}{\partial x} G(x, \xi)\).

Aún tenemos que determinar\(C\). Podemos hacer esto usando la discontinuidad de salto de la derivada:

\[\dfrac{\partial G\left(\xi^{+}, \xi\right)}{\partial x}-\dfrac{\partial G\left(\xi^{-}, \xi\right)}{\partial x}=\dfrac{1}{p(\xi)} \nonumber \]

Por nuestro problema\(p(x)=1\). Entonces, insertando la función de nuestro Green, tenemos

\ [\ begin {alineado}
1 &=\ dfrac {\ parcial G\ izquierda (\ xi^ {+},\ xi\ derecha)} {\ x parcial} -\ dfrac {\ parcial G\ izquierda (\ xi^ {-},\ xi\ derecha)} {\ x parcial}\\
&=\ dfrac {\ parcial} {\ x parcial} [C\ sin\ omega (1-x)\ sin\ omega\ xi] _ {x=\ xi} -\ dfrac {\ parcial} {\ parcial} {\ x parcial} [C\ sin\ omega (1-\ xi)\ sin\ omega x] _ {x=\ xi}\\
&=-\ omega C\ cos\ omega (1-\ xi)\ sin\ omega\ xi-\ omega C\ sin\ omega (1-\ xi)\ cos\ omega\ xi\
&=-\ omega C\ sin\ omega (\ xi+1-\ xi)\\
&=-\ omega C\ sin\ omega.
\ end {alineado}\ etiqueta {8.49}\]

Por lo tanto,

\[C=-\dfrac{1}{\omega \sin \omega} . \nonumber \]

Por último, tenemos la función de nuestro Green:

\ [G (x,\ xi) =\ izquierda\ {\ comenzar {matriz} {l}
-\ dfrac {\ sin\ omega (1-\ xi)\ sin\ omega x} {\ omega\ sin\ omega}, 0\ leq x\ leq\ xi\
-\ dfrac {\ sin\ omega (1-x)\ sin\ omega\ xi} {\ omega\ sin\ omega},\ xi\ leq x\ leq 1
\ end {array}. \ derecho. \ label {8.50}\]

Es instructivo comparar este resultado con el resultado de Variación de Parámetros. Tenemos las funciones\(y_{1}(x)=\sin \omega x\) y\(y_{2}(x)=\sin \omega(1-x)\) como las soluciones de la ecuación homogénea satisfaciendo\(y_{1}(0)=0\) y\(y_{2}(1)=0\). Tenemos que computar\(p W\):

\ [\ begin {alineado}
p (x) W (x) &=y_ {1} (x) y_ {2} ^ {\ prime} (x) -y_ {1} ^ {\ prime} (x) y_ {2} (x)\\
&=-\ omega\ sin\ omega x\ cos\ omega (1-x) -\ omega\ cos\ omega x\ sin\ omega (x)\\
&=-\ omega\ sin\ omega
\ fin {alineado}\ etiqueta {8.51}\]

Al insertar este resultado en el resultado Variación de parámetros para la función del Verde, se obtiene la misma función de Verde que la anterior.

8.3.1 La función Dirac Delta

Desarrollaremos una teoría más general de las funciones de Green para ecuaciones diferenciales ordinarias que abarca algunas de las propiedades enumeradas. La función de Green satisface una ecuación diferencial homogénea para\(x \neq \xi\),

\[\dfrac{\partial}{\partial x}\left(p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right)+q(x) G(x, \xi)=0, \quad x \neq \xi . \label{8.52} \]

Cuando\(x=\xi\), vimos que la derivada tiene un salto en su valor. Esto es similar a la función step, o Heaviside,

\ (H (x) =\ left\ {\ begin {array} {l}
1, x>0\\
0, x<0
\ end {array}\ right.\)

En el caso de la función step, la derivada es cero en todas partes excepto en el salto. En el salto, hay una pendiente infinita, aunque técnicamente, hemos aprendido que no hay derivado en este punto. Intentaremos remediar esto introduciendo la función delta de Dirac,

\[\delta(x)=\dfrac{d}{d x} H(x) . \nonumber \]

Luego mostraremos que la función del Verde satisface la ecuación diferencial

\[\dfrac{\partial}{\partial x}\left(p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right)+q(x) G(x, \xi)=\delta(x-\xi) . \label{8.53} \]

La función delta de Dirac,\(\delta(x)\), es un ejemplo de lo que se conoce como una función generalizada, o una distribución. Dirac había introducido esta función en la década de 1930 en su estudio de la mecánica cuántica como herramienta útil. Posteriormente se estudió en una teoría general de las distribuciones y se encontró que era más que una simple herramienta utilizada por los físicos. La función delta de Dirac, como cualquier distribución, solo tiene sentido bajo una integral.

Antes de definir la función delta de Dirac e introducir algunas de sus propiedades, veremos algunas representaciones que conducen a la definición. Consideraremos los límites de dos secuencias de funciones.

Primero definimos la secuencia de funciones

\ (f_ {n} (x) =\ izquierda\ {\ begin {array} {l}
0, |x|>\ dfrac {1} {n}\\
\ dfrac {n} {2}, |x|<\ dfrac {1} {n}
\ end {array}\ derecha.\)

Esta es una secuencia de funciones como se muestra en la Figura 8.1. Como\(n \rightarrow \infty\), encontramos que el límite es cero para\(x \neq 0\) y es infinito para\(x=0\). Sin embargo, el área debajo de cada miembro de las secuencias es una ya que cada caja tiene altura\(\dfrac{n}{2}\) y ancho\(\dfrac{2}{n}\). Así, la función limitante es cero en la mayoría de los puntos pero tiene área uno. (¡En este punto el lector que es nuevo en esto debería estar rascándose la cabeza!)

Figura 8.1. Una trama de las funciones\(f_{n}(x)\) para\(n=2,4,8\).

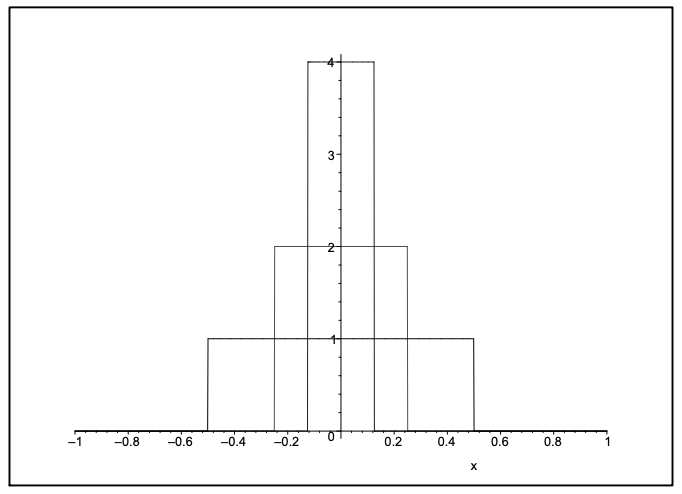
El límite no es realmente una función. Es una función generalizada. Se llama la función delta de Dirac, que se define por

1. \(\delta(x)=0\)para\(x \neq 0\).
2. \(\int_{-\infty}^{\infty} \delta(x) d x=1\).

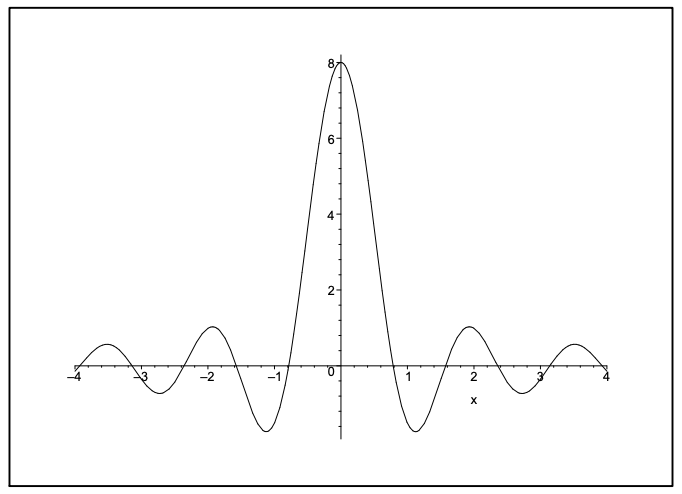
Otro ejemplo es la secuencia definida por

\[D_{n}(x)=\dfrac{2 \sin n x}{x} . \label{8.54} \]

Podemos graficar esta función. Primero reescribimos esta función como

\[D_{n}(x)=2 n \dfrac{\sin n x}{n x} . \nonumber \]

Ahora es fácil verlo como\(x \rightarrow 0, D_{n}(x) \rightarrow 2 n\). Para grandes\(x\), La función tiende a cero. Una gráfica de esta función se encuentra en la Figura 8.2. Para grandes\(n\) el pico crece y los valores de\(D_{n}(x)\) para\(x \neq 0\) tienden a cero como se muestra en la Figura 8.3.
Observamos que en el límite\(n \rightarrow \infty, D_{n}(x)=0\) para\(x \neq 0\) y es infinito en\(x=0\). Sin embargo, usando análisis complejos se puede demostrar que el área es

\[\int_{-\infty}^{\infty} D_{n}(x) d x=2 \pi \nonumber \]

Así, el área es constante para cada uno\(n\).

Figura 8.2. Una gráfica de la función\(D_n(x)\) para\(n = 4\).

Figura 8.3. Una gráfica de la función\(D_n(x)\) para\(n = 40\).

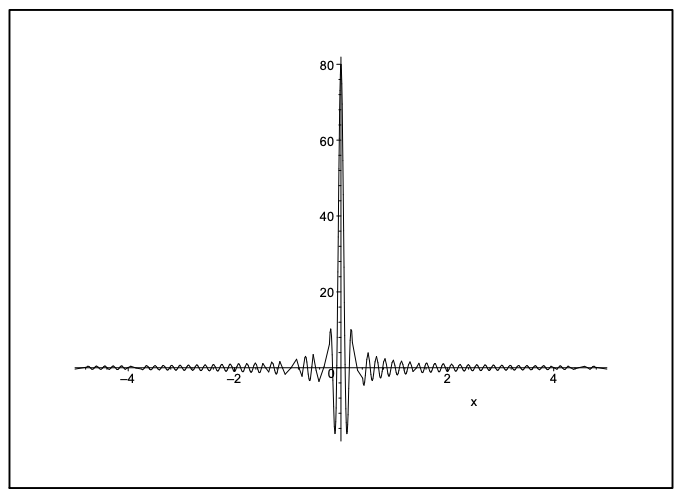
Hay dos propiedades principales que definen una función delta de Dirac. Primero tiene que el área bajo la función delta es una,

\[\int_{-\infty}^{\infty} \delta(x) d x=1 \nonumber \]

La integración en intervalos más generales da

\[\int_{a}^{b} \delta(x) d x=1, \quad 0 \in[a, b] \nonumber \]

y

\[\int_{a}^{b} \delta(x) d x=0, \quad 0 \notin[a, b] . \nonumber \]

Otra propiedad común es lo que a veces se llama la propiedad tamizada. Es decir, integrar el producto de una función y la función delta “tamiza” un valor específico de la función. Está dado por

\[\int_{-\infty}^{\infty} \delta(x-a) f(x) d x=f(a) \nonumber \]

Esto se puede ver al señalar que la función delta es cero en todas partes excepto en\(x=a\). Por lo tanto, el integrando es cero en todas partes y la única contribución de\(f(x)\) será de\(x=a\). Entonces, podemos sustituir por\(f(x)\)\(f(a)\) debajo de la integral. Ya que\(f(a)\) es una constante, tenemos que

\[\int_{-\infty}^{\infty} \delta(x-a) f(x) d x=\int_{-\infty}^{\infty} \delta(x-a) f(a) d x=f(a) \int_{-\infty}^{\infty} \delta(x-a) d x=f(a) . \nonumber \]

Otra propiedad resulta del uso de un argumento escalado,\(a x\). En este caso demostramos que

\[\delta(a x)=|a|^{-1} \delta(x) . \label{8.55} \]

Como es habitual, esto sólo tiene sentido bajo un signo integral. Entonces, colocamos\(\delta(a x)\) dentro de una integral y hacemos una sustitución\(y=a x\):

\ [\ comenzar {alineado}
\ int_ {-\ infty} ^ {\ infty}\ delta (a x) d x &=\ lim _ {L\ fila derecha\ infty}\ int_ {-L} ^ {L}\ delta (a x) d x\
&=\ lim _ {L\ fila derecha\ infty}\ dfrac {1} {a}\ int_ {-a L} ^ {a L}\ delta (y) d y
\ final {alineado}\ etiqueta {8.56}\]

Si\(a>0\) entonces

\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{a} \int_{-\infty}^{\infty} \delta(y) d y . \nonumber \]

Sin embargo, si\(a<0\) entonces

\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{a} \int_{\infty}^{-\infty} \delta(y) d y=-\dfrac{1}{a} \int_{-\infty}^{\infty} \delta(y) d y . \nonumber \]

La diferencia general en un signo menos multiplicativo puede ser absorbida en una expresión cambiando el factor\(1 / a\) a\(1 /|a|\). Así,

\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{|a|} \int_{-\infty}^{\infty} \delta(y) d y . \label{8.57} \]

Ejemplo 8.6. Evaluar\(\in_{-\infty}^{\infty}(5x+1) \delta(4(x-2))dx\). This is a straight forward integration:

\[\int_{-\infty}^{\infty}(5 x+1) \delta(4(x-2)) d x=\dfrac{1}{4} \int_{-\infty}^{\infty}(5 x+1) \delta(x-2) d x=\dfrac{11}{4} \nonumber \]

Una escala más general del argumento toma la forma\(\delta(f(x))\). La integral de se\(\delta(f(x))\) puede evaluar dependiendo del número de ceros de\(f(x)\). Si solo hay un cero,\(f\left(x_{1}\right)=0\), entonces uno tiene ese

\[\int_{-\infty}^{\infty} \delta(f(x)) d x=\int_{-\infty}^{\infty} \dfrac{1}{\left|f^{\prime}\left(x_{1}\right)\right|} \delta\left(x-x_{1}\right) d x \nonumber \]

Esto se puede probar usando la sustitución\(y=f(x)\) y se deja como un ejercicio para el lector. Este resultado suele escribirse como

\[\delta(f(x))=\dfrac{1}{\left|f^{\prime}\left(x_{1}\right)\right|} \delta\left(x-x_{1}\right) . \nonumber \]

Ejemplo 8.7. Evaluar\(\int_{-\infty}^{\infty} \delta(3x-2)x^2dx\).

Esto no es un simple\(\delta(x-a)\). Entonces, necesitamos encontrar los ceros de\(f(x)=3 x-2\). Sólo hay uno,\(x=\dfrac{2}{3}\). También,\(\left|f^{\prime}(x)\right|=3\). Por lo tanto, tenemos

\[\int_{-\infty}^{\infty} \delta(3 x-2) x^{2} d x=\int_{-\infty}^{\infty} \dfrac{1}{3} \delta\left(x-\dfrac{2}{3}\right) x^{2} d x=\dfrac{1}{3}\left(\dfrac{2}{3}\right)^{2}=\dfrac{4}{27} \nonumber \]

Tenga en cuenta que esta integral puede ser evaluada a la larga mediante el uso de la sustitución\(y=3 x-2\). Entonces,\(d y=3 d x\) y\(x=(y+2) / 3\). Esto da

\[\int_{-\infty}^{\infty} \delta(3 x-2) x^{2} d x=\dfrac{1}{3} \int_{-\infty}^{\infty} \delta(y)\left(\dfrac{y+2}{3}\right)^{2} d y=\dfrac{1}{3}\left(\dfrac{4}{9}\right)=\dfrac{4}{27} . \nonumber \]

Más generalmente, uno puede mostrar que cuando\(f\left(x_{j}\right)=0\) y\(f^{\prime}\left(x_{j}\right) \neq 0\) para\(x_{j}\)\(j=1,2, \ldots, n\), (es decir; cuando uno tiene $n$ ceros simples), entonces

\[\delta(f(x))=\sum_{j=1}^{n} \dfrac{1}{\left|f^{\prime}\left(x_{j}\right)\right|} \delta\left(x-x_{j}\right) . \nonumber \]

Ejemplo 8.8. Evaluar\(\int_0^{2 \pi} \cos x \delta \left( x^2 - \pi^2 \right)dx\).

En este caso el argumento de la función delta tiene dos raíces simples. A saber,\(f(x)=x^{2}-\pi^{2}=0\) cuándo\(x=\pm \pi\). Además,\(f^{\prime}(x)=2 x\). Por lo tanto,\(\left|f^{\prime}(\pm \pi)\right|=2 \pi\). Esto da

\[\delta\left(x^{2}-\pi^{2}\right)=\dfrac{1}{2 \pi}[\delta(x-\pi)+\delta(x+\pi)] . \nonumber \]

Insertando esta expresión en la integral y señalando que no\(x=-\pi\) está en el intervalo de integración, tenemos

\ [\ begin {alineado}
\ int_ {0} ^ {2\ pi}\ cos x\ delta\ izquierda (x^ {2} -\ pi^ {2}\ derecha) d x &=\ dfrac {1} {2\ pi}\ int_ {0} ^ {2\ pi}\ cos x [\ delta (x-\ pi) +\ delta (x+\ pi)] d x\\
&=\ dfrac {1} {2\ pi}\ cos\ pi=-\ dfrac {1} {2\ pi}
\ final {alineado}\ etiqueta {8.58}\]

Finalmente, anteriormente notamos que existe una relación entre la función Heaviside, o step, y la función delta de Dirac. Definimos la función Heaviside como

\ (H (x) =\ left\ {\ begin {array} {l}
0, x<0\\
1, x>0
\ end {array}\ right.\)

Entonces, es fácil verlo\(H^{\prime}(x)=\delta(x)\).

8.3.2 Ecuación diferencial de función de Green

Como se señaló, la función de Green satisface la ecuación diferencial

\[\dfrac{\partial}{\partial x}\left(p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right)+q(x) G(x, \xi)=\delta(x-\xi) \label{8.59} \]

y satisface condiciones homogéneas. Hemos utilizado la función de Green para resolver la ecuación no homogénea

\[\dfrac{d}{d x}\left(p(x) \dfrac{d y(x)}{d x}\right)+q(x) y(x)=f(x) . \label{8.60} \]

Estas ecuaciones se pueden escribir en las formas más compactas

\ [\ begin {reunió}
\ mathcal {L} [y] =f (x)\\
\ mathcal {L} [G] =\ delta (x-\ xi).
\ final {reunido}\ etiqueta {8.61}\]

Multiplicando la primera ecuación por\(G(x, \xi)\), la segunda ecuación por\(y(x)\), y luego restando, tenemos

\[G \mathcal{L}[y]-y \mathcal{L}[G]=f(x) G(x, \xi)-\delta(x-\xi) y(x) . \nonumber \]

Ahora, integrar ambos lados de\(x=a\) a\(x=b\). El lado izquierdo se convierte en

\[\int_{a}^{b}[f(x) G(x, \xi)-\delta(x-\xi) y(x)] d x=\int_{a}^{b} f(x) G(x, \xi) d x-y(\xi) \nonumber \]

y, usando Green's Identity, el lado derecho es

\[\int_{a}^{b}(G \mathcal{L}[y]-y \mathcal{L}[G]) d x=\left[p(x)\left(G(x, \xi) y^{\prime}(x)-y(x) \dfrac{\partial G}{\partial x}(x, \xi)\right)\right]_{x=a}^{x=b} \nonumber \]

Combinando estos resultados y reordenando, obtenemos

\[y(\xi)=\int_{a}^{b} f(x) G(x, \xi) d x-\left[p(x)\left(y(x) \dfrac{\partial G}{\partial x}(x, \xi)-G(x, \xi) y^{\prime}(x)\right)\right]_{x=a}^{x=b} \label{8.62} \]

A continuación, se utilizan las condiciones de límite en el problema para determinar qué condiciones necesita satisfacer la función de Green. Por ejemplo, si tenemos la condición de límite\(y(a)=0\) y\(y(b)=0\), entonces los términos límite ceden

\ [\ begin {alineado}
y (\ xi) =&\ int_ {a} ^ {b} f (x) G (x,\ xi) d x-\ izquierda [p (b)\ izquierda (y (b)\ dfrac {\ parcial G} {\ x parcial} (b,\ xi) -G (b,\ xi) y^ {\ prime} (b)\ derecha) derecha\]\\
&+\ izquierda [p (a)\ izquierda (y (a)\ dfrac {\ parcial G} {\ parcial x} (a,\ xi) -G (a,\ xi) y^ {\ prime} (a)\ derecha)\ derecha]\\
=&\ int_ {a} ^ {b} f (x) G (x,\ xi) d x+p (b) G (b,\ xi) y^ {\ prime} (b) -p (a) G (a,\ xi) y^ {\ prime} (a).
\ end {alineado}\ etiqueta {8.63}\]

El lado derecho sólo se desvanecerá si\(G(x, \xi)\) además satisface estas condiciones de límite homogéneas. Esto luego nos deja con la solución

\[y(\xi)=\int_{a}^{b} f(x) G(x, \xi) d x . \nonumber \]

Deberíamos reescribir esto en función de\(x\). Entonces, reemplazamos\(\xi\) con\(x\) y\(x\) con\(\xi\). Esto da

\[y(x)=\int_{a}^{b} f(\xi) G(\xi, x) d \xi . \nonumber \]

Sin embargo, esto aún no está en la forma deseable. Se invierten los argumentos de la función del Verde. Pero,\(G(x, \xi)\) es simétrico en sus argumentos. Entonces, podemos simplemente cambiar los argumentos obteniendo el resultado deseado.

Ahora podemos ver que la teoría funciona para otras condiciones límite. Si lo hubiéramos hecho\(y^{\prime}(a)=0\), entonces el\(y(a) \dfrac{\partial G}{\partial x}(a, \xi)\) término en los términos límite podría hacerse desvanecer si nos fijamos\(\dfrac{\partial G}{\partial x}(a, \xi)=0\). Entonces, esto confirma que se pueden plantear otros problemas de valor límite además del que se ha elaborado en el capítulo hasta el momento.

Incluso podemos adaptar esta teoría a condiciones de límite no homogéneas. Primero reescribimos la ecuación (8.62) como

\[y(x)=\int_{a}^{b} G(x, \xi) f(\xi) d \xi-\left[p(\xi)\left(y(\xi) \dfrac{\partial G}{\partial \xi}(x, \xi)-G(x, \xi) y^{\prime}(\xi)\right)\right]_{\xi=a}^{\xi=b} . \label{8.64} \]

Consideremos las condiciones de contorno\(y(a)=\alpha\) y\(y^{\prime}(b)= beta\). También asumimos que\(G(x, \xi)\) satisface condiciones de frontera homogéneas,

\[G(a, \xi)=0, \quad \dfrac{\partial G}{\partial \xi}(b, \xi)=0 . \nonumber \]

en ambos\(x\) y\(\xi\) ya que la función del Verde es simétrica en sus variables. Entonces, solo necesitamos enfocarnos en los términos límite para examinar el efecto en la solución. Tenemos

\ [\ comenzar {alineado}
{\ izquierda [p (\ xi)\ izquierda (y (\ xi)\ dfrac {\ parcial G} {\ parcial\ xi} (x,\ xi) -G (x,\ xi) y^ {\ prime} (\ xi)\ derecha)\ derecha] _ {\ xi=a} ^ {\ xi=b}} &=\ izquierda [p (b)\ izquierda (y (b)\ dfrac {\ parcial G} {\ parcial\ xi} (x, b) -G (x, b) y^ {\ prime} (b)\ derecha)\ derecha]\\
&- izquierda [p (a)\ izquierda (y (a)\ dfrac {\ parcial G} {\ parcial\ xi} (x, a) -G (x, a) y^ {\ prime} (a)\ derecha)\ derecha. \\
&=-\ beta p (b) G (x, b) -\ alfa p (a)\ dfrac {\ parcial G} {\ parcial\ xi} (x, a)
\ final {alineado}\ etiqueta {8.65}\]

Por lo tanto, tenemos la solución

\[y(x)=\int_{a}^{b} G(x, \xi) f(\xi) d \xi+\beta p(b) G(x, b)+\alpha p(a) \dfrac{\partial G}{\partial \xi}(x, a) . \label{8.66} \]

Esta solución satisface las condiciones de límite no homogéneas. Veamos cómo funciona.

Ejemplo 8.9. Modificar Ejemplo 8.4. para resolver el problema del valor límite\(y'' = x^2, \quad y(0)=1, y(1)=2\) using the boundary value Green's function that we found:

\ [G (x,\ xi) =\ left\ {\ begin {array} {l}
-\ xi (1-x), 0\ leq\ xi\ leq x\\
-x (1-\ xi), x\ leq\ xi\ leq 1
\ end {array}. \ derecho. \ label {8.67}\]

Insertamos la función de Green en la solución y utilizamos las condiciones dadas para obtener

\ [\ begin {alineado}
y (x) &=\ int_ {0} ^ {1} G (x,\ xi)\ xi^ {2} d\ xi-\ izquierda [y (\ xi)\ dfrac {\ parcial G} {\ parcial\ xi} (x,\ xi) -G (x,\ xi) y^ {\ prime} (\ xi)\ xi)\ derecha] _ {xi=0} ^ {\ xi=1}\\
&=\ int_ {0} ^ {x} (x-1)\ xi^ {3} d\ xi+\ int_ {x} ^ {1} x (\ xi-1)\ xi^ {2} d\ xi+y (0)\ dfrac {\ parcial G} {\ parcial\ xi} ( x, 0) -y (1)\ dfrac {\ parcial G} {\ parcial\ xi} (x, 1)\\
&=\ dfrac {(x-1) x^ {4}} {4} +\ dfrac {x\ izquierda (1-x^ {4}\ derecha)} {4} -\ dfrac {x\ izquierda (1-x^ {3}\ derecha)} {3} + (x-1) -2 x\\
&=\ dfrac {x^ {4}} {12} +\ dfrac {35} {12} x-1
\ end {alineado}\ etiqueta {8.68}\]

Por supuesto, este problema se puede resolver de manera más directa mediante la integración directa. La solución general es

\[y(x)=\dfrac{x^{4}}{12}+c_{1} x+c_{2} . \nonumber \]

Al insertar esta solución en cada condición de contorno se obtiene el mismo resultado.

Hemos visto cómo la introducción de la función delta de Dirac en la ecuación diferencial satisfecha por la función de Green, Ecuación (8.59), puede conducir a la solución de problemas de valor límite. La función delta de Dirac también ayuda en nuestra interpretación de la función de Green. Observamos que la función de Green es una solución de una ecuación en la que se encuentra la función no homogénea\(\delta(x-\xi)\). Tenga en cuenta que si multiplicamos la función delta por\(f(\xi)\) e integramos obtenemos

\[\int_{-\infty}^{\infty} \delta(x-\xi) f(\xi) d \xi=f(x) \nonumber \]

Podemos ver la función delta como un impulso unitario en el\(x=\xi\) que se puede utilizar para construir\(f(x)\) como una suma de impulsos de diferentes fortalezas,\(f(\xi)\). Así, la función del Verde es la respuesta al impulso gobernado por la ecuación diferencial y las condiciones límite dadas.

En particular, la ecuación forzada de función delta se puede utilizar para derivar la condición de salto. Comenzamos con la ecuación en la forma

\[\dfrac{\partial}{\partial x}\left(p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right)+q(x) G(x, \xi)=\delta(x-\xi) . \label{8.69} \]

Ahora, integrar ambos lados de\(\xi-\epsilon\) a\(\xi+\epsilon\) y tomar el límite como\(\epsilon \rightarrow 0\). Entonces,

\ [\ begin {alineado}
\ lim _ {\ épsilon\ fila derecha 0}\ int_ {\ xi-\ épsilon} ^ {\ xi+\ épsilon}\ izquierda [\ dfrac {\ parcial} {\ x parcial}\ izquierda (p (x)\ dfrac {\ parcial G (x,\ xi)} {\ parcial x}\ derecha) +q (x) G (x,\ xi)\ derecha] d x &=\ lim _ {\ épsilon\ fila derecha 0}\ int_ {\ xi-\ épsilon} ^ {\ xi+\ épsilon}\ delta (x-\ xi) d x\\
&=1.
\ end {alineado}\ etiqueta {8.70}\]

Dado que el\(q(x)\) término es continuo, el límite de ese término se desvanece. Usando el Teorema Fundamental del Cálculo, tenemos

\[\lim _{\epsilon \rightarrow 0}\left[p(x) \dfrac{\partial G(x, \xi)}{\partial x}\right]_{\xi-\epsilon}^{\xi+\epsilon}=1 . \label{8.71} \]

¡Esta es la condición de salto que hemos estado usando!