2.2.E: Mejores aproximaciones afín (ejercicios)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Ejercicio2.2.E.1
Encuentra la derivada de cada una de las siguientes funciones.
a)f(t)=(t3,t,2t+4)
b)g(t)=(3tcos(2t),4tsin(2t))
c)h(t)=(4t3−3,sin(t),e−2t)
d)f(t)=(e−tsin(3t),e−tcos(3t),te−t)
- Responder
-
a)Df(t)=(3t2,1,2)
c)Dh(t)=(12t2,cos(t),−2e−2t)
Ejercicio2.2.E.2
Para cada una de las siguientes, encuentra la mejor aproximación afín af en el punto dado.
a)f(t)=(t,t3),t=2
b)f(t)=(3sin(2t),4cos(2t)),t=π6
c)f(t)=(cos(t),sin(t),cos(2t)),t=π3
d)f(t)=(2cos(2t),3sin(2t),3t),t=0
- Responder
-
a)A(t)=(1,12)(t−2)+(2,8)
c)A(t)=(−√32,12,−√3)(t−π3)+(12,√32,−12)
Ejercicio2.2.E.3
Deje quef(t)=(2cos(πt),3sin(πt)) entre parametrizar una elipseE R2. TrazarE junto con la línea tangente enf(23).
Ejercicio2.2.E.4
Dejarf(t)=((1+2cos(t))cos(t),(1+2cos(t))sin(t)) parametrizar una curvaC enR2. TrazarC junto con la línea tangente enf(π6).
Ejercicio2.2.E.5
Dejarh(t)=(sin(2πt),cos(2πt),t2) parametrizar una héliceH circularR3. TrazarH junto con la línea tangente enh(32).
Ejercicio2.2.E.6
Dejarg(t)=(cos(πt),√t,sin(πt)) parametrizar una curvaC enR3. TrazarC junto con la línea tangente eng(14).
Ejercicio2.2.E.7
Supongamos quef:R→R2 se define porf(t)=(t,φ(t)), dondeφ:R→R es diferenciable, y dejar queC sea la curva enR2 parametrizada porf. Mostrar que la línea tangente aC atf(c) es la misma que la línea tangente a la gráfica deφ at(c,φ(c).
- Responder
-
Tenga en cuenta que la línea tangente aC atf(c) está parametrizada por
A(t)=(1,φ′(c))(t−c)+(c,φ(c))=(t,φ′(c)(t−c)+φ(c))
Ejercicio2.2.E.8
DejarC ser la curva enR2 parametrizada porf(t)=(t3,t6),−∞<t<∞. Esf una parametrización suave deC? Si no, ¿se puede encontrar una parametrización suave deC?
- Responder
-
No, nof es una parametrización suave deC desde entoncesDf(0)=(0,0). Sin embargog(t)=(t,t2),−∞<t<∞,, es una parametrización suave deC.
Ejercicio2.2.E.9
DejarC ser la curva enR2 parametrizada porf(t)=(t2,t2),−∞<t<∞. Demostrar que nof es una parametrización suave deC. ¿Dónde está el problema? TrazarC e identificar la ubicación del problema.
- Responder
-
fno es una parametrización suave deC desde entoncesDf(0)=(0,0).
Ejercicio2.2.E.10
Dejarv≠0 yp ser vectores enRn y dejarC ser la curva enRn parametrizada porf(t)=tv+p. ¿Cuál es la mejor aproximación afín af att=t0?
Ejercicio2.2.E.11
Para cada una de las siguientes, encuentra el vector tangente unitario y el vector normal de unidad principal en el punto indicado.
a)f(t)=(t,t2),t=1
b)g(t)=(3sin(2t),3cos(2t)),t=π3
c)f(t)=(2cos(t),4sin(t)),t=π4
d)h(t)=(cos(πt),2sin(πt)),t=34
e)g(t)=(cos(t),sin(t),t),t=π3
f)f(t)=(2sin(t),3cos(2t),2t),t=π4
g)f(t)=(sin(πt),−cos(πt),3t),t=12
h)g(t)=(cos(πt2),sin(πt2),t2),t=1
i)f(t)=(t,t2,t3),t=2
- Responder
-
a)T(1)=1√5(1,2);N(1)=1√5(−2,1)
c)T(π4)=1√5(−1,2);N(π4)=−1√5(2,1)
e)T(π3)=(−12√32,12√2,1√2);N(π3)=(−12,−√32,0)
g)T(12)=(0,π√9+π2,3√9+π2);N(12)=(−1,0,0)
i)T(2)=1√161(1,4,12);N(2)=1√29141(−76,−143,54)
Ejercicio2.2.E.12
Usa el hecho de quef(t)=(bcos(t),bsin(t)) parametriza un círculo de radiob para mostrar que un radio de un círculo siempre es perpendicular a la línea tangente en el punto donde el radio toca el círculo.
Ejercicio2.2.E.13
Verificar (2.2.21); es decir, mostrar que sif:R→Rn yφ:R→R son ambos diferenciables, entonces
D(φ(t)f(t))=φ(t)Df(t)+φ′(t)f(t).
Ejercicio2.2.E.14
Supongamosf:R→R3 y ambosg:R→R3 son diferenciables. Demostrar que
D(f(t)×g(t))=f(t)×Dg(t)+Df(t)×g(t),
otra versión más de la regla del producto.
Ejercicio2.2.E.15
La siguiente figura ilustra una curva en R2 parametrizada por alguna funciónf:R→R2. SiT es el vector tangente unitario en el punto indicado en la curva, entonces cualquieraM oN es el vector normal de unidad principal en ese punto. ¿Cuál es?
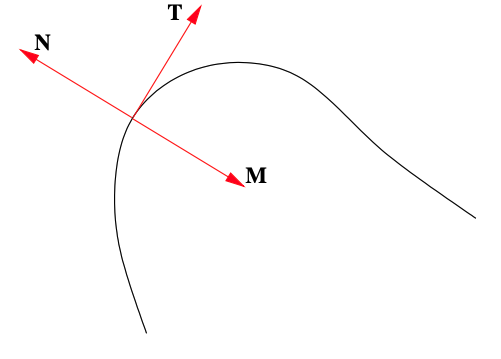
- Responder
-
M


