2.3: Movimiento a lo largo de una curva
- Page ID
- 111718
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Velocidad y Aceleración
Considera una partícula moviéndose en el espacio para que su posición en el tiempo\(t\) sea dada por\(\mathbf{x}(t)\). Pensamos que\(\mathbf{x}(t)\) se mueve a lo largo de una curva\(C\) parametrizada por una función\(f\), donde\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\). De ahí que tengamos\(\mathbf{x}(t)=f(t)\), o, más simplemente,\(\mathbf{x}=f(t)\). Para nosotros, siempre\(n\) serán 2 o 3, pero hay situaciones físicas en las que es razonable tener valores mayores de\(n\), y la mayor parte de lo que hacemos en esta sección se aplicará a esos casos igualmente bien. Este también es un buen momento para introducir la notación Leibniz para un derivado, escribiendo así
\[ \frac{d \mathbf{x}}{d t}=D f(t). \]
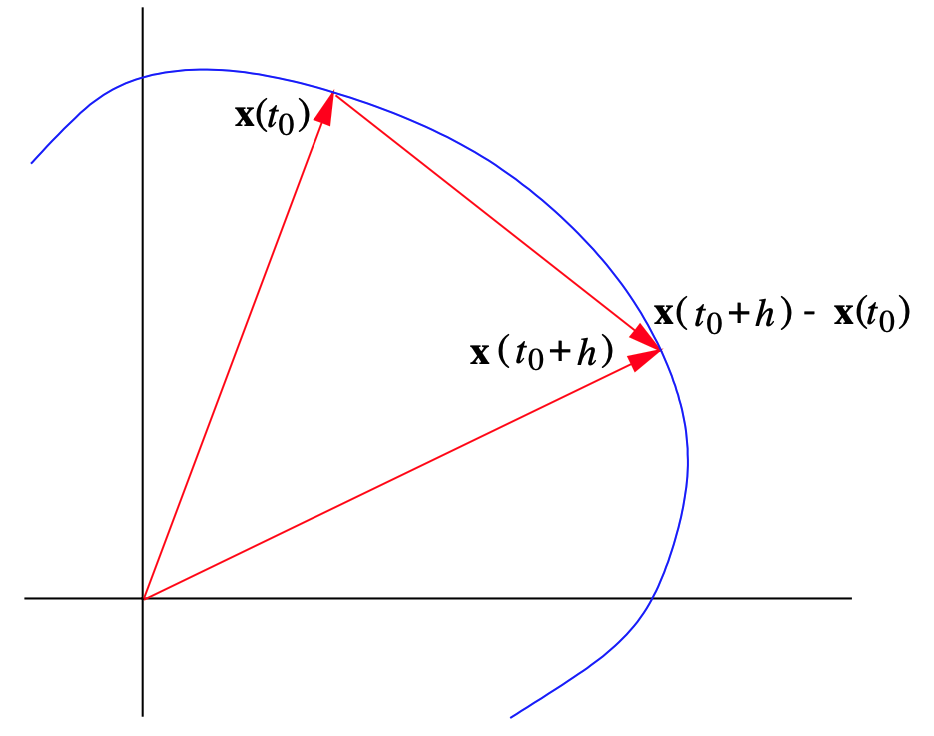
En un momento dado\(t_0\), el vector\(\mathbf{x}\left(t_{0}+h\right)-\mathbf{x}\left(t_{0}\right)\) representa la magnitud y dirección del cambio de posición de la partícula\(t_0\) a lo largo\(C\) de tiempo en tiempo\(t_0 + h\), como se muestra en la Figura 2.3.1. Dividiendo por\(h\), obtenemos un vector,
\[ \frac{\mathbf{x}\left(t_{0}+h\right)-\mathbf{x}\left(t_{0}\right)}{h}, \]
con la misma dirección, pero con longitud que se aproxima a la velocidad promedio de la partícula en el intervalo de tiempo de\(t_0\) a\(t_0 + h\). Asumiendo la diferenciabilidad y tomando el límite como\(h\) se acerca a 0, tenemos la siguiente definición.
Definición\(\PageIndex{1}\)
Supongamos\(\mathbf{x}(t)\) es la posición de una partícula en el momento\(t\) moviéndose a lo largo de una curva\(C\) en\(\mathbb{R}^n\). Llamamos
\[ \mathbf{v}(t)=\frac{d}{d t} \mathbf{x}(t) \]
la velocidad de la partícula en el momento\(t\) y llamamos
\[ s(t)=\|\mathbf{v}(t)\| \]
la velocidad de la partícula en el momento\(t\). Además, llamamos
\[ \mathbf{a}(t)=\frac{d}{d t} \mathbf{v}(t) \]
la aceleración de la partícula en el momento\(t\).
Ejemplo\(\PageIndex{1}\)
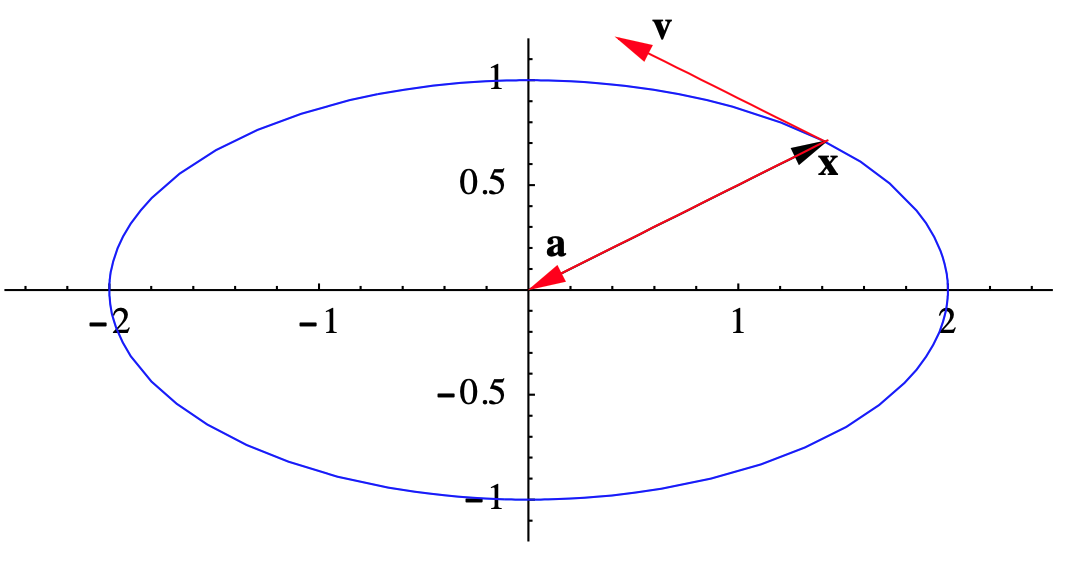
Considera que una partícula se mueve a lo largo de una elipse para que su posición en cualquier momento\(t\)
\[\mathbf{x}=(2 \cos (t), \sin (t)). \nonumber \]
Entonces su velocidad es
\[ \mathbf{v}=(-2 \sin (t), \cos (t)) , \nonumber \]
su velocidad es
\[ s=\sqrt{4 \sin ^{2}(t)+\cos ^{2}(t)}=\sqrt{3 \sin ^{2}(t)+1}, \nonumber \]
y su aceleración es
\[ \mathbf{a}=(-2 \cos (t),-\sin (t)). \nonumber \]
Por ejemplo, en\(t=\frac{\pi}{4}\) tenemos
\ [\ comenzar {reunido}
\ izquierda. \ mathbf {x}\ derecha|_ {t=\ frac {\ pi} {4}} =\ izquierda (\ sqrt {2},\ frac {1} {\ sqrt {2}}\ derecha),\\
\ izquierda. \ mathbf {v}\ derecha|_ {t=\ frac {\ pi} {4}} =\ izquierda (-\ sqrt {2},\ frac {1} {\ sqrt {2}}\ derecha),\
\\ izquierda.s\ derecha|_ {t=\ frac {\ pi} {4}} =\ sqrt {\ frac {5} {2},
\ end {reunido}\]
y
\[ \left.\mathbf{a}\right|_{t=\frac{\pi}{4}}=\left(-\sqrt{2},-\frac{1}{\sqrt{2}}\right) \text { . } \nonumber \]
Ver Figura 2.3.2. Observe que, en este ejemplo,\(\mathbf{a}=-\mathbf{x}\) para todos los valores de\(t\).
Curvatura
Supongamos que\(\mathbf{x}\) es la posición,\(\mathbf{v}\) es la velocidad,\(s\) es la velocidad, y\(\mathbf{a}\) es la aceleración, en el tiempo\(t\), de una partícula que se mueve a lo largo de una curva\(C\). Dejar\(T(t)\) ser el vector tangente unitario y\(N(t)\) ser el vector normal de la unidad principal en\(\mathbf{x}\). Ahora
\[ T(t)=\frac{\frac{d \mathbf{x}}{d t}}{\left\|\frac{d \mathbf{x}}{d t}\right\|}=\frac{\mathbf{v}}{\|\mathbf{v}\|}=\frac{\mathbf{v}}{s} , \]
por lo
\[\mathbf{v}=s\|T(t)\|. \]
Así
\[ \mathbf{a}=\frac{d \mathbf{v}}{d t}=\frac{d}{d t} s T(t)=\frac{d s}{d t} T(t)+s D T(t) \]
Desde
\[ N(t)=\frac{D T(t)}{\|D T(t)\|} ,\]
tenemos
\[ \mathbf{a}=\frac{d s}{d t} T(t)+s\|D T(t)\| N(t) . \label{2.3.10} \]
Tenga en cuenta que (\(\ref{2.3.10}\)) expresa la aceleración de una partícula como la suma de múltiplos escalares del vector tangente unitario y el vector normal de la unidad principal. Es decir,
\[ \mathbf{a}=a_{T} T(t)+a_{N} N(t) ,\]
donde
\[ a_{T}=\frac{d s}{d t} \]
y
\[ a_{N}=s\|D T(t)\|.\]
Sin embargo, ya que\(T(t)\) y\(N(t)\) son vectores unitarios ortogonales, también tenemos
\ [\ begin {align}
\ mathbf {a}\ cdot T (t) &=\ izquierda (a_ {T} T (t) +a_ {N} N (t)\ derecha)\ cdot T (t)\ nonumber\\
&=a_ {T} (T (t)\ cdot T (t)) +a_ {N} (T (t)\ cdot N (t))\ etiqueta {2.3.14}\\
&=a_ {T}\ nonumber
\ end {align}\]
y
\ [\ begin {align}
\ mathbf {a}\ cdot N (t) &=\ izquierda (a_ {T} T (t) +a_ {N} N (t)\ derecha)\ cdot N (t) c\ nonumber\\
&=a_ {T} (T (t)\ cdot N (t)) +a_ {N} (N (t)\ cpunto N (t))\ etiqueta {2.3.15}\\
&=a_ {N}. \ nonumber
\ end {align}\]
De ahí\(a_T\) es la coordenada de\(\mathbf{a}\) en la dirección de\(T(t)\) y\(a_N\) es la coordenada de\(\mathbf{a}\) en la dirección de\(N(t)\). Así (\(\ref{2.3.10}\)) escribe la aceleración como una suma de su componente en la dirección del vector tangente unitario y su componente en la dirección del vector normal de la unidad principal. En particular, esto demuestra que la aceleración se encuentra en el plano determinado por\(T(t)\) y\(N(t)\). Además,\(a_T\) es la tasa de cambio de velocidad, mientras que\(a_N\) es el producto de la velocidad\(s\) y\(\|D T(t)\|\), la magnitud de la tasa de cambio del vector tangente unitario. Ya que\(\|T(t)\|=1\) para todos\(t\),\(\|D T(t)\|\) refleja solo la velocidad a la que\(T(t)\) está cambiando la dirección de; en otras palabras,\(\|D T(t)\|\) es una medida de la rapidez con la que cambia en el momento la dirección de la partícula que\(C\) se mueve a lo largo de la curva\(t\). Si dividimos esto por la velocidad de la partícula, obtenemos una medida estándar de la tasa de cambio de dirección de\(C\) sí misma.
Definición\(\PageIndex{2}\)
Dada una curva\(C\) con parametrización suave\(\mathbf{x}=f(t)\), llamamos
\[ \kappa=\frac{\|D T(t)\|}{s(t)} \label{2.3.16}\]
la curvatura de\(C\) at\(f(t)\).
Usando (\(\ref{2.3.16}\)), podemos reescribir (\(\ref{2.3.10}\)) como
\[ \mathbf{a}=\frac{d s}{d t} T(t)+s^{2} \kappa N(t) . \label{2.3.17} \]
De ahí que la coordenada de aceleración en la dirección del vector tangente es la tasa de cambio de la velocidad y la coordenada de aceleración en la dirección del vector normal principal es el cuadrado de la velocidad por la curvatura. Así, cuanto mayor sea la velocidad o cuanto más apretada sea la curva, mayor será el tamaño del componente normal de aceleración; cuanto mayor sea la velocidad a la que aumenta la velocidad, mayor es el componente tangencial de la aceleración. Es por ello que se aconseja a los conductores que disminuyan la velocidad mientras se acercan a una curva, y luego que aceleren mientras conducen por la curva.
Ejemplo\(\PageIndex{2}\)
Supongamos que una partícula se mueve a lo largo de una línea de\(\mathbb{R}^n\) manera que su posición en cualquier momento\(t\) viene dada por
\[ \mathbf{x}=t \mathbf{w}+\mathbf{p} , \nonumber \]
donde\(\mathbf{w} \neq 0\) y\(\mathbf{p}\) son vectores en\(\mathbb{R}^n\). Entonces la partícula tiene velocidad
\[ \mathbf{v}=\frac{d \mathbf{x}}{d t}=\mathbf{w} \nonumber \]
y velocidad\(\boldsymbol{s}=\|\mathbf{w}\|\), por lo que el vector tangente unitario es
\[ T(t)=\frac{\mathbf{v}}{s}=\frac{\mathbf{w}}{\|\mathbf{w}\|} . \nonumber \]
Por lo tanto\(T(t)\) es un vector constante, así\(D T(t)=\mathbf{0}\) y
\[ \kappa=\frac{\|D T(t)\|}{s}=0 \nonumber \]
para todos\(t\). En otras palabras, una línea tiene curvatura cero, como debemos esperar ya que el vector tangente nunca cambia de dirección.
Ejemplo\(\PageIndex{3}\)
Considera que una partícula se mueve a lo largo\(C\) \(\mathbb{R}^2\)de un círculo de radio\(r>0\) y centro\((a,b)\), con su posición en el tiempo dada por
\[ \mathbf{x}=(r \cos (t)+a, r \sin (t)+b) . \nonumber \]
Entonces su velocidad, velocidad y aceleración son
\ begin {reunió}
\ mathbf {v} =( -r\ sin (t), r\ cos (t)),\\
s=\ sqrt {\ izquierda.r^ {2}\ sin ^ {(} t\ derecha) +r^ {2}\ cos ^ {2} (t)} =r
\ end {reunidos}
y
\[\mathbf{a}=(-r \cos (t),-r \sin (t)) , \nonumber \]
respectivamente. Por lo tanto, el vector tangente unitario es
\[ T(t)=\frac{\mathbf{v}}{s}=(-\sin (t), \cos (t)) . \nonumber \]
Así
\[ D T(t)=(-\cos (t),-\sin (t)) \nonumber \]
y
\[ \|D T(t)\|=\sqrt{\cos ^{2}(t)+\sin ^{2}(t)}=1 .\nonumber \]
De ahí que la curvatura de\(C\) es, para todos\(t\),
\[ \kappa=\frac{\|D T(t)\|}{s}=\frac{1}{r} .\nonumber \]
Así, un círculo tiene una curvatura constante, es decir, el recíproco del radio del círculo. En particular, cuanto mayor es el radio de un círculo, menor es la curvatura. También, tenga en cuenta que
\[ \frac{d s}{d t}=\frac{d}{d t} r=0 , \nonumber \]
entonces, de (\(\ref{2.3.10}\)), tenemos
\[ \mathbf{a}=r N(t) , \nonumber \]
que podemos verificar directamente. Es decir, la aceleración tiene un componente normal, pero ningún componente tangencial.
Ejemplo\(\PageIndex{4}\)
Ahora considera que una partícula se mueve a lo largo de una elipse\(E\) para que su posición en cualquier momento\(t\) sea
\[ \mathbf{x}=(2 \cos (t), \sin (t)) .\nonumber \]
Entonces, como vimos anteriormente, la velocidad y velocidad de la partícula son
\[ \mathbf{v}=(-2 \sin (t), \cos (t)) \nonumber \]
y
\[s=\sqrt{3 \sin ^{2}(t)+1} ,\nonumber \]
respectivamente. Para fines de diferenciación, será útil reescribir\(s\) como
\[ s=\sqrt{\frac{3}{2}(1-\cos (2 t))+1}=\sqrt{\frac{5-3 \cos (2 t)}{2}} . \nonumber \]
Entonces el vector tangente unitario es
\[ T(t)=\sqrt{\frac{2}{5-3 \cos (2 t)}}(-2 \sin (t), \cos (t)) . \nonumber \]
Así
\[ D T(t)=\sqrt{\frac{2}{5-3 \cos (2 t)}}(-2 \cos (t),-\sin (t))-\frac{3 \sqrt{2} \sin (2 t)}{(5-3 \cos (2 t))^{\frac{3}{2}}}(-2 \sin (t), \cos (t)) . \nonumber \]
Entonces, por ejemplo, en\(t=\frac{\pi}{4}\), tenemos
\ [\ comenzar {reunido}
\ izquierda. \ mathbf {x}\ derecha|_ {t=\ frac {\ pi} {4}} =\ izquierda (\ sqrt {2},\ frac {1} {\ sqrt {2}}\ derecha),\\
\ izquierda. \ mathbf {v}\ derecha|_ {t=\ frac {\ pi} {4}} =\ izquierda (-\ sqrt {2},\ frac {1} {\ sqrt {2}}\ derecha),\
\\ izquierda.s\ derecha|_ {t=\ frac {\ pi} {4}} =\ sqrt {\ frac {5} {2},
\ end {reunido}\]
\ [\ comenzar {alineado}
T\ izquierda (\ frac {\ pi} {4}\ derecha) &=\ frac {1} {\ sqrt {5}} (-2,1),\\
D T\ izquierda (\ frac {\ pi} {4}\ derecha) &=-\ frac {1} {5\ sqrt {5}} (4,8),
\ end {alineado}\]
y
\[ \left\|D T\left(\frac{\pi}{4}\right)\right\|=\frac{1}{5 \sqrt{5}} \sqrt{16+64}=\frac{4}{5} . \nonumber \]
Por lo tanto, la curvatura de\(E\) at\(\left(\sqrt{2}, \frac{1}{\sqrt{2}}\right)\) es
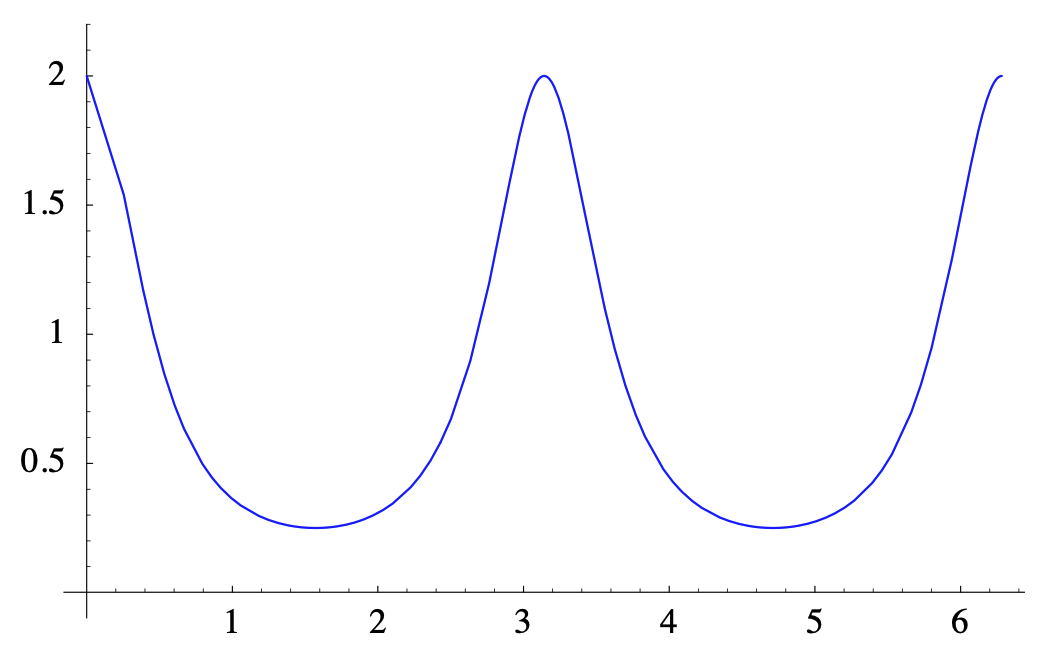
\[ \left.\kappa\right|_{t=\frac{\pi}{4}}=\frac{\frac{4}{5}}{\sqrt{\frac{5}{2}}}=\frac{4 \sqrt{2}}{5 \sqrt{5}}=0.05060 , \nonumber \]
donde el valor numérico final se ha redondeado a cuatro decimales. Aunque la expresión general para κ es complicada, es fácilmente computada y trazada usando un sistema de álgebra computacional, como se muestra en la Figura 2.3.3. Comparando esto con la gráfica de esta elipse en la Figura 2.3.2, podemos ver por qué la curvatura es mayor alrededor de (2, 0) y (−2, 0), correspondiente a\(t=0\),\(t=\pi \), y\(t=2 \pi \), y más pequeña en (0, 1) y (0, −1), correspondiente a\(t=\frac{\pi}{2}\) y \(t=\frac{3 \pi}{2}\). Por último, como vimos anteriormente, la aceleración de la partícula es
\[ \mathbf{a}=(-2 \cos (t),-\sin (t)), \nonumber \]
por lo
\[ \left.\mathbf{a}\right|_{t=\frac{\pi}{4}}=\left(-\sqrt{2},-\frac{1}{\sqrt{2}}\right) . \nonumber \]
Ahora si escribimos
\[ \left.\mathbf{a}\right|_{t=\frac{\pi}{4}}=a_{T} T(t)+a_{N} N(t), \nonumber \]
entonces podemos calcular, usando (\(\ref{2.3.17}\)),
\[ a_{T}=\left.\frac{d s}{d t}\right|_{t=\frac{\pi}{4}}=\frac{1}{\sqrt{2}}(5-3 \cos (2 t))^{-\frac{1}{2}}\left(\left.3 \sin (2 t)\right|_{t=\frac{\pi}{4}}=\frac{3}{\sqrt{10}}\right. \nonumber \]
y
\[ a_{N}=\left.\left.s^{2}\right|_{t=\frac{\pi}{4}} k\right|_{t=\frac{\pi}{4}}=\frac{5}{2} \frac{4 \sqrt{2}}{5 \sqrt{5}}=\frac{2 \sqrt{2}}{\sqrt{5}}=\frac{4}{\sqrt{10}}, \nonumber \]
o, utilizando (\(\ref{2.3.14}\)) y (\(\ref{2.3.15}\)),
\[ a_{T}=\left.\mathbf{a}\right|_{t=\frac{\pi}{4}} \cdot T\left(\frac{\pi}{4}\right)=\left(-\sqrt{2},-\frac{1}{\sqrt{2}}\right) \cdot \frac{1}{\sqrt{5}}(-2,1)=\frac{3}{\sqrt{10}} \nonumber \]
y
\[ a_{N}=\left.\mathbf{a}\right|_{t=\frac{\pi}{4}} \cdot N\left(\frac{\pi}{4}\right)=\left(-\sqrt{2},-\frac{1}{\sqrt{2}}\right) \cdot \frac{1}{4 \sqrt{5}}(-4,-8)=\frac{4}{\sqrt{10}}. \nonumber \]
De ahí que, en cualquiera de los casos,
\[ \left.\mathbf{a}\right|_{t=\frac{\pi}{4}}=\frac{3}{\sqrt{10}} T\left(\frac{\pi}{4}\right)+\frac{4}{\sqrt{10}} N\left(\frac{\pi}{4}\right) . \nonumber \]
Longitud del arco
Supongamos que una partícula se mueve a lo largo de una curva\(C\) de\(\mathbb{R}^n\) manera que su posición en el tiempo\(t\) viene dada por\(\mathbf{x}=f(t)\) y dejar que\(D\) sea la distancia recorrida por la partícula de tiempo\(t=a\) a \(t=b\). Supondremos que\(s(t)=\|\mathbf{v}(t)\|\) es continuo en\( [a,b] \). Para aproximar\(D\),\( [a,b]\) dividimos en\(n\) subintervalos, cada uno de longitud
\[ \Delta t=\frac{b-a}{n}, \nonumber \]
y etiquetar los extremos de los subintervalos\(a=t_{0}, t_{1}, \ldots, t_{n}=b\). Si\(\Delta t\) es pequeña, entonces la distancia que recorre la partícula durante el subintervalo\(j\) th,\(j=1,2, \ldots, n\), debe ser, aproximadamente,\(s \Delta t\), una aproximación que mejora a medida que\( \Delta t\) disminuye. Por lo tanto, para suficientemente pequeños\(\Delta t\) (equivalentemente, suficientemente grandes\(n\)),
\[ \sum_{j=1}^{n} s\left(t_{j-1}\right) \Delta t \label{2.3.18} \]
proporcionará una aproximación tan cercana a\(D\) como se desee. Es decir, debemos definir
\[ D=\lim _{n \rightarrow \infty} \sum_{j=1}^{n} s\left(t_{j-1}\right) \Delta t . \label{2.3.19} \]
Pero (\(\ref{2.3.18}\)) es una suma de Riemann (en particular, una suma de reglas de la izquierda) que se aproxima a la integral definida
\[ \int_{a}^{b} s(t) d t . \label{2.3.20} \]
De ahí que el límite in (\(\ref{2.3.19}\)) sea el valor de la integral definida (\(\ref{2.3.20}\)), y así tenemos la siguiente definición.
Definición\(\PageIndex{3}\)
Supongamos que una partícula se mueve a lo largo\(C\) de una curva de\(\mathbb{R}^n\) manera que su posición en el tiempo\(t\) viene dada por\(\mathbf{x}=f(t)\). Supongamos que la velocidad\(\mathbf{v}(t)\) es continua en el intervalo\([a,b]\). Luego definimos la distancia recorrida por la partícula de vez en cuando\(t=a\) \(t=b\)para ser
\[ \int_{a}^{b}\|\mathbf{v}(t)\| d t . \label{2.3.21} \]
Tenga en cuenta que la distancia recorrida es la longitud de la curva\(C\) si la partícula atraviesa\(C\) exactamente una vez. En ese caso, llamamos (\(\ref{2.3.21}\)) la longitud de\(C\). En general, para cualquier\(t\) tal que el intervalo\([a,t]\) esté en el dominio de\(f\), podemos calcular
\[ \sigma(t)=\int_{a}^{t}\|\mathbf{v}(u)\| d u , \]
que llamamos la función de longitud de arco para\(C\).
Ejemplo\(\PageIndex{5}\)
Considere la hélice\(H\) parametrizada por
\[ f(t)=(\cos (t), \sin (t), t) . \nonumber \]
Si dejamos\(L\) denotar la longitud de un bucle completo de la hélice, entonces una partícula que viaja a lo largo de\(H\) acuerdo a\(\mathbf{x}=f(t)\) atravesará esta distancia a medida que\(t\) va de 0 a\(2\pi\). Desde
\[ \mathbf{v}(t)=(-\sin (t), \cos (t), 1) , \nonumber \]
tenemos
\[ \|\mathbf{v}(t)\|=\sqrt{\sin ^{2}(t)+\cos ^{2}(t)+1}=\sqrt{2} .\nonumber \]
De ahí
\[ L=\int_{0}^{2 \pi} \sqrt{2} d t=2 \sqrt{2} \pi . \nonumber \]
Ejemplo\(\PageIndex{6}\)
Supongamos que una partícula se mueve a lo largo de una curva de\(C\) manera que su posición en\(t\) el tiempo viene
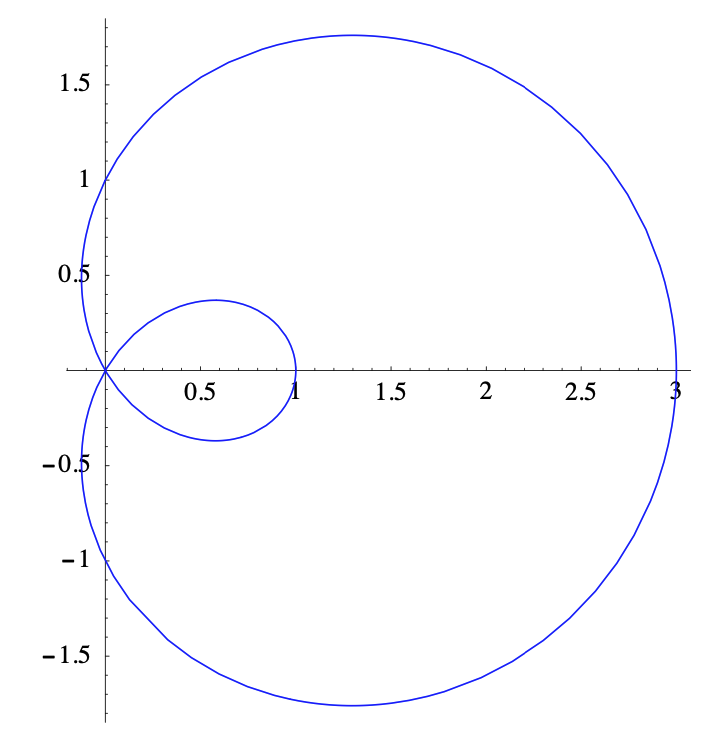
\[ \mathbf{x}=((1+2 \cos (t)) \cos (t),(1+2 \cos (t)) \sin (t)) . \nonumber \]
Entonces\(C\) está la curva en la Figura 2.3.4, que se llama limaçon. La partícula atravesará esta curva una vez a medida\(t\) que va de 0 a\(2\pi\). Ahora
\[ \mathbf{v}=\left(-(1+2 \cos (t)) \sin (t)-2 \sin (t) \cos (t),(1+2 \cos (t)) \cos (t)-2 \sin ^{2}(t)\right) , \nonumber \]
por lo
\ begin {alineado}
\ |\ mathbf {v}\ |^ {2} =&\ mathbf {v}\ cdot\ mathbf {v}\\
=& (1+2\ cos (t)) ^ {2}\ sin ^ {2} (t) +4 (1+2\ cos (t))\ sin ^ {2} (t)\ cos (t) +4\ sin ^ {2} (t)\ cos ^ {2} (t),\\
&\ cuádruple + (1+2\ cos (t)) ^ {2}\ cos ^ {2} (t) -4 (1+2\ cos (t))\ sin ^ {2} (t)\ cos (t) +4\ sin ^ {4} (t)\\
=& (1+2\ cos (t)) ^ {2}\ izquierda (\ sin ^ {2} (t) +\ cos ^ {2} (t)\ derecha) +4\ sin ^ {2} (t)\ cos ^ {2} (t) +4\ sin ^ {4} (t)\\
=& (1+2\ cos (t)) ^ {2} +4\ sin ^ {2} (t)\ cos ^ {2} (t) +4\ sin ^ {4} (t)
\ fin {alineado}
Por lo tanto, la longitud de\(C\) es
\[ \int_{0}^{2 \pi} \sqrt{(1+2 \cos (t))^{2}+4 \sin ^{2}(t) \cos ^{2}(t)+4 \sin ^{4}(t)} d t=13.3649 , \nonumber \]
donde la integración se realizó con una computadora y el resultado final se redondeó a cuatro decimales. Obsérvese que integrando de 0 a\(4\pi\) encontraría la distancia que recorre la partícula dando vueltas\(C\) dos veces, es decir,
\[ \int_{0}^{4 \pi} \sqrt{(1+2 \cos (t))^{2}+4 \sin ^{2}(t) \cos ^{2}(t)+4 \sin ^{4}(t)} d t=26.7298 . \nonumber \]


