3.3: Mejores aproximaciones afín

Mejores aproximaciones afín

Dada una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y un punto\(\mathbf{c}\), deseamos encontrar la función afín\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) que mejor se aproxime\(f\) para los puntos cercanos a\(\mathbf{c}\). Como antes, lo mejor significará que el resto funcione,

\[ R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h}) , \]

se aproxima a 0 a una velocidad suficientemente rápida. En este contexto, dado que\(R(\mathbf{h})\) es un escalar y\(\mathbf{h}\) es un vector, suficientemente rápido significará que

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{R(\mathbf{h})}{\|\mathbf{h}\|}=0 . \label{3.3.2}\]

Generalizando nuestra notación anterior, diremos que una función que\(R: \mathbb{R}^{n} \rightarrow \mathbb{R}\) satisface la Ecuación\ ref {3.3.2} es\(o(\mathbf{h})\). Obsérvese que si\(n=1\) esta definición ampliada de\(o(\mathbf{h})\) equivale a la definición dada en la Sección 2.2.

Definición\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define sobre una bola abierta que contiene el punto\(\mathbf{c}\). Llamamos a una función afín\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) la mejor aproximación afín a\(f\) at\(\mathbf{c}\) if (1)\(A(\mathbf{c})=f(\mathbf{c})\) y (2)\(R(\mathbf{h}) \text { is } o(\mathbf{h})\), donde

\[ R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h}) . \]

Supongamos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y supongamos\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\). Dado que\(A\) es afín, existe una función lineal\(L: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y un escalar\(b\) tal que

\[ A(\mathbf{x})=L(\mathbf{x})+b \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^n\). Desde entonces\(A(\mathbf{c})=f(\mathbf{c})\), tenemos

\[ f(\mathbf{c})=L(\mathbf{c})+b, \]

lo que implica que

\[ b=f(\mathbf{c})-L(\mathbf{c}) . \]

De ahí

\[ A(\mathbf{x})=L(\mathbf{x})+f(\mathbf{c})-L(\mathbf{c})=L(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^n\). Además, si dejamos

\[ \mathbf{a}=\left(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\right) , \]

donde\(\mathbf{e}_{1}, \mathbf{e}_{2}, \ldots, \mathbf{e}_{n}\) están, como de costumbre, los vectores base estándar para\(\mathbb{R}^n\), entonces, de nuestros resultados en la Sección 1.5,

\[ L(\mathbf{x})=\mathbf{a} \cdot \mathbf{x} \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^n\). De ahí

\[ A(\mathbf{x})=\mathbf{a} \cdot(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) , \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^n\), y vemos que\(A\) está completamente determinado por el vector\(\mathbf{a}\)

Definición\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define sobre una bola abierta que contiene el punto\(\mathbf{c}\). Si\(f\) tiene una mejor aproximación afín a\(\mathbf{c}\), entonces decimos que\(f\) es diferenciable en\(\mathbf{c}\). Además, si la mejor aproximación afín a\(f\) at\(\mathbf{c}\) viene dada por

\[ A(\mathbf{x})=\mathbf{a} \cdot(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) , \]

entonces llamamos\(\mathbf{a}\) el derivado de\(f\) at\(\mathbf{c}\) y escribimos\(D f(\mathbf{c})=\mathbf{a}\).

Ahora supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\mathbf{c}\) con la mejor aproximación afín\(A\) y dejar\(\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)=D f(\mathbf{c})\). Desde

\[ R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h})=f(\mathbf{c}+\mathbf{h})-\mathbf{a} \cdot \mathbf{h}-f(\mathbf{c}) \]

es\(o(\mathbf{h})\), debemos tener

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{R(\mathbf{h})}{\|\mathbf{h}\|}=0 . \]

En particular, para\(k=1,2, \ldots, n\), si lo dejamos\(\mathbf{h}=t \mathbf{e}_{k}\), entonces se\(\mathbf{h}\) acerca\(\mathbf{0}\) como se\(t\) acerca a 0, entonces

\[ 0=\lim _{t \rightarrow 0} \frac{R\left(t \mathbf{e}_{k}\right)}{\left\|t \mathbf{e}_{k}\right\|}=\lim _{t \rightarrow 0} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-t\left(\mathbf{a} \cdot \mathbf{e}_{k}\right)-f(\mathbf{c})}{|t|}=\lim _{t \rightarrow 0} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-t a_{k}-f(\mathbf{c})}{|t|} \nonumber \]

Primero considerando\(t>0\), tenemos

\[ 0=\lim _{t \rightarrow 0^{+}} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-t a_{k}-f(\mathbf{c})}{t}=\lim _{t \rightarrow 0^{+}}\left(\frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-f(\mathbf{c})}{t}-a_{k}\right) , \]

lo que implica que

\[ a_{k}=\lim _{t \rightarrow 0^{+}} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-f(\mathbf{c})}{t} . \]

Con\(t<0\), tenemos

\[ 0=\lim _{t \rightarrow 0^{-}} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-t a_{k}-f(\mathbf{c})}{-t}=-\lim _{t \rightarrow 0^{-}}\left(\frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-f(\mathbf{c})}{t}-a_{k}\right), \]

lo que implica que

\[ a_{k}=\lim _{t \rightarrow 0^{-}} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-f(\mathbf{c})}{t} . \]

De ahí

\[ a_{k}=\lim _{t \rightarrow 0} \frac{f\left(\mathbf{c}+t \mathbf{e}_{k}\right)-f(\mathbf{c})}{t}=\frac{\partial}{\partial x_{k}} f(\mathbf{c}) . \]

Así hemos demostrado que

\[ \mathbf{a}=\left(\frac{\partial}{\partial x_{1}} f(\mathbf{c}), \frac{\partial}{\partial x_{2}} f(\mathbf{c}), \ldots, \frac{\partial}{\partial x_{n}} f(\mathbf{c})\right)=\nabla f(\mathbf{c}) . \]

Teorema\(\PageIndex{1}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\mathbf{c}\), entonces

\[ D f(\mathbf{c})=\nabla f(\mathbf{c}) \]

Ahora se deduce que si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\mathbf{c}\), entonces la mejor aproximación afín a\(f\) at\(\mathbf{c}\) es

\[ A(\mathbf{x})=\nabla f(\mathbf{c}) \cdot(\mathbf{x}-\mathbf{c})-f(\mathbf{c}) . \]

Sin embargo, lo contrario no se sostiene: es posible\(\nabla f(\mathbf{c})\) que exista incluso cuando no\(f\) es diferenciable en\(\mathbf{c}\). Antes de mirar un ejemplo, tenga en cuenta que si\(f\) es diferenciable en\(\mathbf{c}\) y\(A\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\), entonces, ya que\(R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h})\) es\(o(\mathbf{h})\),

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}}(f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h}))=\lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{R(\mathbf{h})}{\|\mathbf{h}\|}\|\mathbf{h}\|=0\|\mathbf{0}\|=0 . \]

Ahora\(A\) es continuo en\(\mathbf{c}\), por lo que se deduce que

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} f(\mathbf{c}+\mathbf{h})=\lim _{\mathbf{h} \rightarrow \mathbf{0}} A(\mathbf{c}+\mathbf{h})=A(\mathbf{c})=f(\mathbf{c}) . \]

En otras palabras,\(f\) es continuo en\(\mathbf{c}\).

Teorema\(\PageIndex{2}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\mathbf{c}\), entonces\(f\) es continuo en\(\mathbf{c}\).

Ejemplo\(\PageIndex{1}\)

Considera la función

\[ g(x, y)= \begin{cases}\frac{x y}{x^{2}+y^{2}}, & \text { if }(x, y) \neq(0,0), \nonumber \\ 0, & \text { if }(x, y)=(0,0) .\end{cases} \nonumber \]

En la Sección 3.1 mostramos que no\(g\) es continuo en (0, 0) y en la Sección 3.2 lo vimos\(\nabla g(0,0)=(0,0)\). Dado que no\(g\) es continuo en (0, 0), ahora se deduce, del teorema anterior, que no\(g\) es diferenciable en (0, 0), aunque el gradiente exista en ese punto. De la gráfica de\(g\) la Figura 3.3.1 (vista originalmente en la Figura 3.1.7), podemos ver que el hecho de que no\(g\) sea diferenciable, de hecho, ni siquiera continuo, en el origen se manifiesta geométricamente como un desgarro en la superficie.

Figura\(\PageIndex{1}\): El gráfico de una función no diferenciable

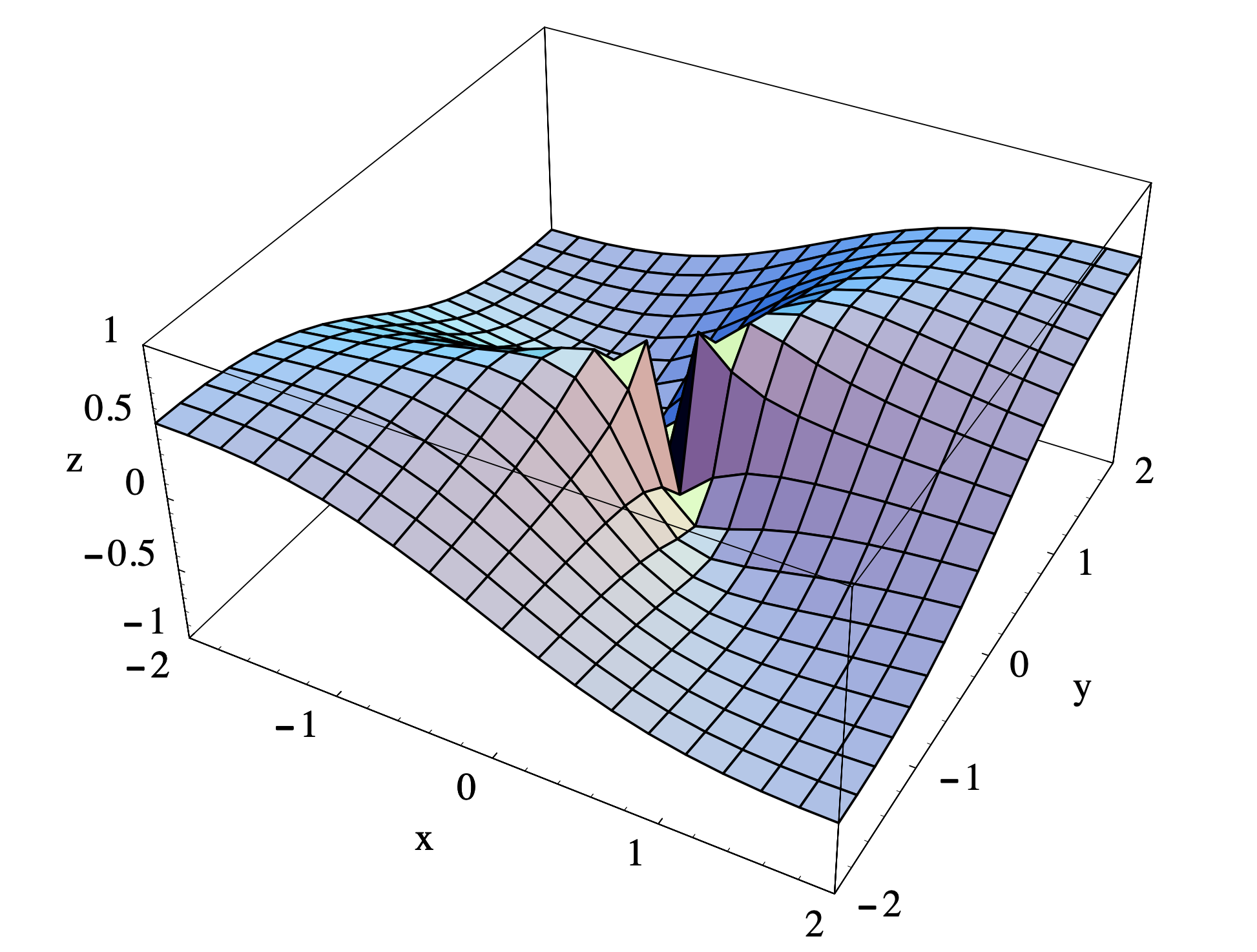
A partir de este ejemplo vemos que la diferenciabilidad de una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) en un punto\(\mathbf{c}\) requiere algo más que la existencia del gradiente de\(f\) at\(\mathbf{c}\). Resulta que la continuidad de las derivadas parciales de\(f\) sobre una bola abierta que contiene\(\mathbf{c}\) suficiente para demostrar que\(f\) es diferenciable en\(\mathbf{c}\). Obsérvese que las derivadas parciales de\(g\) en el ejemplo anterior no son continuas (ver Ejercicio 8 de la Sección 3.2).

Entonces ahora vamos a suponer que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) está\(C^1\) en alguna bola abierta que contiene\(\mathbf{c}\). Si definimos una función afín\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) por

\[ A(\mathbf{x})=\nabla f(\mathbf{c}) \cdot(\mathbf{x}-\mathbf{c})+f(\mathbf{c}) , \]

entonces la función de resto es

\[ R(\mathbf{h})=f(\mathbf{c}+\mathbf{h})-A(\mathbf{c}+\mathbf{h})=f(\mathbf{c}+\mathbf{h})-f(\mathbf{c})-\nabla f(\mathbf{c}) \cdot \mathbf{h} . \]

Tenemos que demostrar que\(R(\mathbf{h})\) es\(o(\mathbf{h})\). Hacia ese fin, para un fijo\(\mathbf{h} \neq \mathbf{0}\), definir\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) por

\[ \varphi(t)=f(\mathbf{c}+t \mathbf{h}) . \]

Primero notamos que\(\varphi\) es diferenciable con

\ [\ begin {align}
\ varphi^ {\ prime} (t) &=\ lim _ {s\ fila derecha 0}\ frac {\ varphi (t+s) -\ varphi (t)} {s}\ nonumber\\
&=\ lim _ {s\ rightarrow 0}\ frac {f (\ mathbf {c} + (t+s)\ mathbf {h}) -f (\ mathbf {c} +t\ mathbf {h})} {s}\ nonúmero\\
&=\ |\ mathbf {h}\ |\ lim _ {s\ fila derecha 0} \ frac {f\ izquierda (\ mathbf {c} +t\ mathbf {h} +s\ |\ mathbf {h}\ |\ frac {\ mathbf {h}} {\ |\ mathbf {h}\ |}\ derecha) -f (\ mathbf {c} +t\ mathbf {h})} {s\ |\ mathbf {h}\ umber\\
&=\ |\ mathbf {h}\ | D_ {\ frac {\ mathbf {h}} {\ |\ mathbf {h}\ |}} f (\ mathbf {c} +t\ mathbf {h})\ nonumber\\
&=\ |\ mathbf {h}\ |\ left (\ nabla f (\ mathbf {c} +t\ mathbf {h})\ cdot\ frac {\ mathbf {h}} {\ |\ mathbf {h}\ |}\ derecha)\ nonumber\\
&=\ nabla f (\ mathbf {c} +t\ mathbf {h})\ cdot\ mathbf {h}\ label {}
\ end {align}\

Del teorema del valor medio del cálculo de una sola variable, se deduce que existe un número\(s\) entre 0 y 1 tal que

\[ \varphi^{\prime}(s)=\varphi(1)-\varphi(0)=f(\mathbf{c}+\mathbf{h})-f(\mathbf{c}) . \]

De ahí que podamos escribir

\[ R(\mathbf{h})=\nabla f(\mathbf{c}+s \mathbf{h}) \cdot \mathbf{h}-\nabla f(\mathbf{c}) \cdot \mathbf{h}=(\nabla f(\mathbf{c}+s \mathbf{h})-\nabla f(\mathbf{c})) \cdot \mathbf{h} . \label{3.3.29} \]

Aplicando la desigualdad Cauchy-Schwarz a (\(\ref{3.3.29}\)),

\[ |R(\mathbf{h})| \leq\|\nabla f(\mathbf{c}+s \mathbf{h})-\nabla f(\mathbf{c})\|\|\mathbf{h}\| , \]

y así

\[ \frac{|R(\mathbf{h})|}{\|\mathbf{h}\|} \leq\|\nabla f(\mathbf{c}+s \mathbf{h})-\nabla f(\mathbf{c})\| . \]

Ahora las derivadas parciales de\(f\) son continuas, por lo que

\ [\ begin {align}
\ lim _ {\ mathbf {h}\ rightarrow\ mathbf {0}}\ |\ nabla f (\ mathbf {c} +s\ mathbf {h}) -\ nabla f (\ mathbf {c})\ | &=\ |\ nabla f (\ mathbf {c} +s\ mathbf {0}) -\ nabla f (\ mathbf {c})\ |\ nonumber\\
&=\ |\ nabla f (\ mathbf {c}) -\ nabla f (\ mathbf {c})\ |\ nonumber\\
&=0. \ label {}
\ end {align}\]

De ahí

\[ \lim _{\mathbf{h} \rightarrow \mathbf{0}} \frac{R(\mathbf{h})}{\|\mathbf{h}\|}=0 . \]

Es decir,\(R(\mathbf{h})\) es\(o(\mathbf{h})\) y\(A\) es la mejor aproximación afín a\(f\) at\(\mathbf{c}\). Así tenemos el siguiente teorema fundamental.

Teorema\(\PageIndex{3}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) está\(C^1\) en una bola abierta que contiene el punto\(\mathbf{c}\), entonces\(f\) es diferenciable en\(\mathbf{c}\).

Ejemplo\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y)=4-2 x^{2}-y^{2} . \nonumber \]

Para encontrar la mejor aproximación afín a\(f\) at (1, 1), primero calculamos

\[ \nabla f(x, y)=(-4 x,-2 y) . \nonumber \]

Así\(\nabla f(1,1)=(-4,-2)\) y\(f(1,1)=1\), así la mejor aproximación afín es

\[ A(x, y)=(-4,-2) \cdot(x-1, y-1)+1 . \nonumber\]

Simplificando, tenemos

\[ A(x, y)=-4 x-2 y+7 . \nonumber \]

Ejemplo\(\PageIndex{3}\)

Supongamos que\(f: \mathbb{R}^{3} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y, z)=\sqrt{x^{2}+y^{2}+z^{2}}. \nonumber \]

Entonces

\[ \nabla f(x, y, z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}(x, y, z) . \nonumber \]

Así, por ejemplo, la mejor aproximación afín a\(f\) at (2, 1, 2) es

\ begin {alineado}
A (x, y, z) &=\ nabla f (2,1,2)\ cdot (x-2, y-1, z-2) +f (2,1,2)\\
&=\ frac {1} {3} (2,1,2)\ cdot (x-2, y-1, z-2) +3\\
&=\ frac {2} {3} (x-2) +\ frac {1} {3} (y-1) +\ frac {2} {3} (z-2) +3\\
&=\ frac {2} {3} x+\ frac {1} {3} y+\ frac {2} {3} z.
\ end {alineado}

Ahora supongamos que dejamos\((x,y,z)\) ser las longitudes de los tres lados de un bloque sólido, en cuyo caso\(f(x,y,z)\) representa la longitud de la diagonal de la caja. Además, supongamos que medimos los lados del bloque y los encontramos que tienen longitudes\(x=2+\epsilon_{x}\),\(y=1+\epsilon_{y}\), y\(z=2+\epsilon_{z}\), dónde\(\left|\epsilon_{x}\right| \leq h\)\(\left|\epsilon_{y}\right| \leq h\), y\(\left|\epsilon_{z}\right| \leq h\) para algún número positivo\(h\) que represente el límite de la precisión de nuestro dispositivo de medición. Ahora estimamos que la diagonal de la caja sea

\[ f(2,1,2)=3 \nonumber\]

con un error de

\ [\ begin {alineado}
\ izquierda|f\ izquierda (2+\ epsilon_ {x}, 1+\ épsilon_ {y}, 2+\ epsilon_ {z}\ derecha) -f (2,1,2)\ derecha| &\ approx\ izquierda|a\ izquierda (2+\ épsilon_ {x}, 1+\ épsilon_ {y}, 2+\ épsilon_ {z}\ derecha) -3\ derecha|\\
&=\ izquierda|\ frac {2} {3}\ épsilon_ {x} +\ frac {1} {3}\ épsilon_ {y} +\ frac {2} {3}\ épsilon_ {z}\ derecha|\\
&\ leq\ frac {2} {3}\ izquierda|\ epsilon_ {x}\ derecha|+\ frac {1} {3}\ izquierda|\ epsilon_ {y}\ derecha|+\ frac {2} {3}\ izquierda|\ epsilon_ {z}\ derecha|\
&\ leq h\ izquierda (\ frac {2} {3} +\ frac {1} {3} +\ frac {2} {3}\ derecha)\\
&=\ frac {5} {3} h.
\ final {alineado}\]

Es decir, esperamos que nuestro error al estimar la diagonal del bloque no sea más que multiplicado por el error máximo en nuestras mediciones de los lados del bloque. Por ejemplo, si el error en nuestras mediciones de longitud está desactivado en no más de ±0. 1 centímetros, entonces nuestra estimación de la diagonal de la caja está apagada en no más de ±0. 17 centímetros.

Tenga en cuenta que si\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es la mejor aproximación afín a\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) at\(\mathbf{c}=\left(c_{1}, c_{2}, \ldots, c_{n}\right) \), entonces la gráfica de\(A\) es el conjunto de todos los puntos\(\left(x_{1}, x_{2}, \ldots, x_{n}, z\right)\) en\(\mathbb{R}^{n+1}\) satisfacer

\[ z=\nabla f(\mathbf{c}) \cdot\left(x_{1}-c_{1}, x_{2}-c_{2}, \ldots, x_{n}-c_{n}\right)+f(\mathbf{c}) .\]

Dejando

\[ \mathbf{n}=\left(\frac{\partial}{\partial x_{1}} f(\mathbf{c}), \frac{\partial}{\partial x_{2}} f(\mathbf{c}), \ldots, \frac{\partial}{\partial x_{n}} f(\mathbf{c}),-1\right) , \]

podemos describir la gráfica de\(A\) como el conjunto de todos los puntos en\(\mathbb{R}^{n+1}\) satisfacer

\[ \mathbf{n} \cdot\left(x_{1}-c_{1}, x_{2}-c_{2}, \ldots, x_{n}-c_{n}, z-f(\mathbf{c})\right)=0 .\]

Así la gráfica de\(A\) es un hiperplano al\(\mathbb{R}^{n+1}\) pasar por el punto\(\left(c_{1}, c_{2}, \ldots, c_{n}, f(\mathbf{c})\right)\) (un punto en la gráfica de\(f\)) con vector normal\(\mathbf{n}\).

Definición\(\PageIndex{3}\)

Si\(A: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es la mejor aproximación afín a\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) at\(\mathbf{c} = \left(c_{1}, c_{2}, \ldots, c_{n}\right) \), entonces llamamos a la gráfica\(A\) del hiperplano tangente a la gráfica de\(f\) at\(\left(c_{1}, c_{2}, \ldots, c_{n}, f(\mathbf{c})\right)\).

Ejemplo\(\PageIndex{4}\)

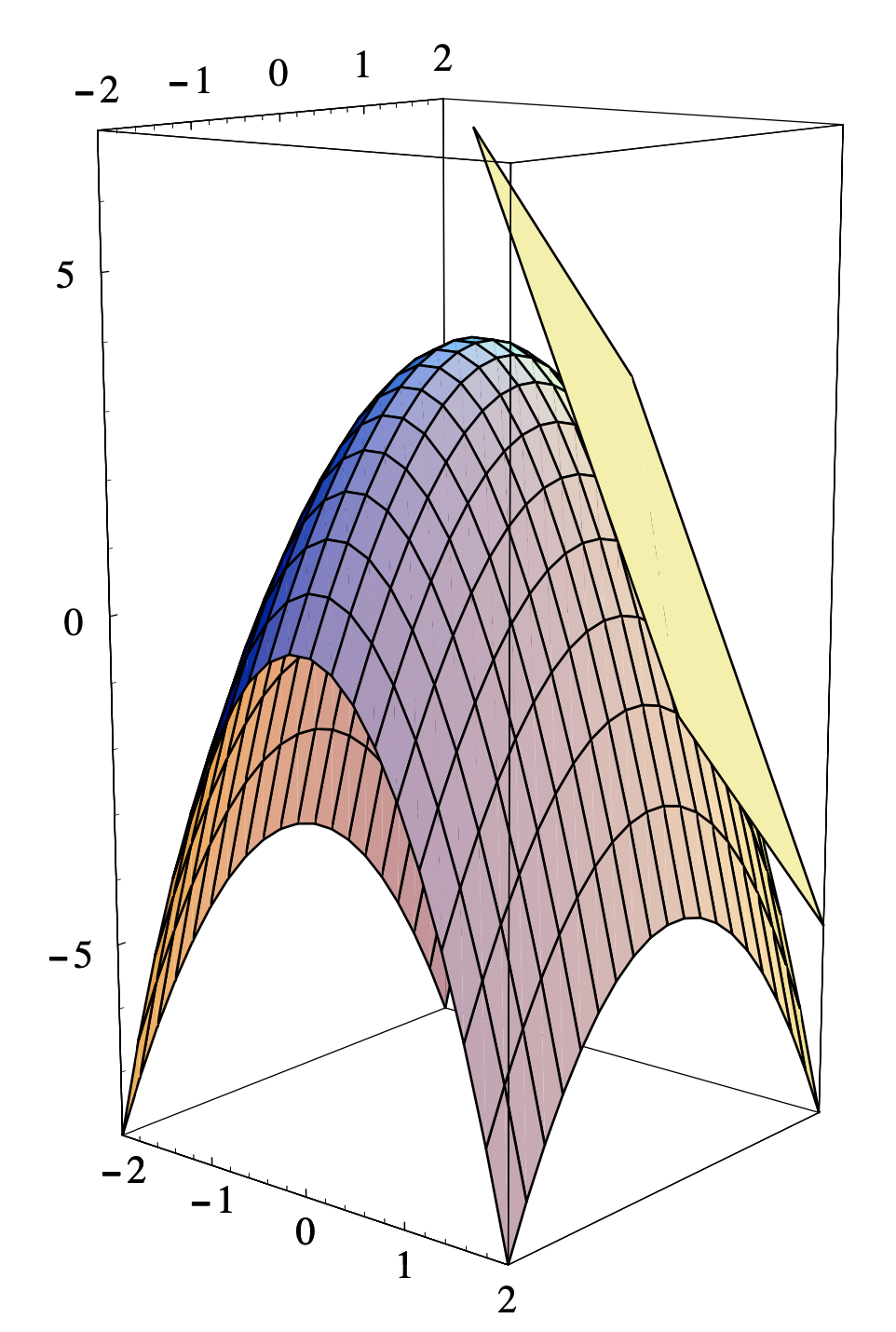
Vimos arriba que la mejor aproximación afín a

\[ f(x, y)=4-2 x^{2}-y^{2} \nonumber \]

en (1,1) es

\[ A(x, y)=7-4 x-2 y . \nonumber \]

De ahí que la ecuación del plano tangente a la gráfica de\(f\) at es

\[ z=7-4 x-2 y , \nonumber \]

o

\[ 4 x+2 y+z=7 . \nonumber \]

Obsérvese que el vector\(\mathbf{n}=(4,2,1)\) es normal al plano tangente, y por lo tanto normal a la gráfica de\(f\) at (1, 1, 1). La gráfica de\(f\) junto con el plano tangente en (1, 1, 1) se muestra en la Figura 3.3.2.

Figura\(\PageIndex{2}\): Un plano tangente a la gráfica de\(f(x, y)=4-2 x^{2}-y^{2}\)

La regla de la cadena

Supongamos que\(\varphi: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es diferenciable en un punto\(c\) y\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en el punto\(\varphi(c)\). Entonces la composición de\(f\) y\(\varphi\) es una función\(f \circ \varphi: \mathbb{R} \rightarrow \mathbb{R}\). Para calcular la derivada de\(f \circ \varphi\) at\(c\), debemos evaluar

\[ (f \circ \varphi)^{\prime}(c)=\lim _{h \rightarrow 0} \frac{f \circ \varphi(c+h)-f \circ \varphi(c)}{h}=\lim _{h \rightarrow 0} \frac{f(\varphi(c+h))-f(\varphi(c))}{h} . \label{3.3.37} \]

Deja\(A\) ser la mejor aproximación afín a\(f\) at\(\mathbf{a}=\varphi(c)\) y let\(\mathbf{k}=\varphi(c+h)-\varphi(c)\). Entonces

\[ f(\varphi(c+h))=f(\mathbf{a}+\mathbf{k})=A(\mathbf{a}+\mathbf{k})+R(\mathbf{k}) , \label{3.3.38} \]

Dónde\(R(\mathbf{k})\) está\(o(\mathbf{k})\). Ahora

\[ A(\mathbf{a}+\mathbf{k})=\nabla f(\mathbf{a}) \cdot \mathbf{k}+f(\mathbf{a}) , \label{3.3.39} \]

por lo

\ [\ begin {align}
f (\ varphi (c+h)) -f (\ varphi (c)) &=f (\ mathbf {a} +\ mathbf {k}) -f (\ mathbf {a})\ nonumber\\
&=\ nabla f (\ mathbf {a})\ cdot\ mathbf {k} +R (\ mathbf {k})\ nonumber\\
&=\ nabla f (\ mathbf {a})\ cdot (\ varphi (c+h) -\ varphi (c)) +R (\ mathbf {k}). \ label {3.3.40}
\ end {align}\]

Sustituyendo (\(\ref{3.3.40}\)) en (\(\ref{3.3.37}\)), tenemos

\ [\ begin {align}
(f\ circ\ varphi) ^ {\ prime} (c) &=\ lim _ {h\ fila derecha 0}\ frac {\ nabla f (\ mathbf {a})\ cdot (\ varphi (c+h) -\ varphi (c)) +R (\ mathbf {k})} {h}\ nonumber\\
=\ lim _ {h\ fila derecha 0}\ nabla f (\ mathbf {a})\ cdot\ frac {\ varphi (c+h) -\ varphi (c)} {h} +\ lim _ {h\ fila derecha 0}\ frac {R (\ mathbf {k})} {h}\ nonumber\\
&=\ nabla f (\ mathbf {a})\ cdot D\ varphi (\ mathbf {c}) +\ lim _ {h\ rightarrow 0}\ frac {R (\ mathbf {k})} {h}. \ label {}
\ end {align}\]

Ahora\(R(\mathbf{k})\) es\(o(\mathbf{k})\), entonces

\[ \lim _{\mathbf{k} \rightarrow \mathbf{0}} \frac{R(\mathbf{k})}{\|\mathbf{k}\|}=0 , \nonumber \]

de lo que se deduce que, para cualquier dado\(\epsilon>0\), tenemos

\[ \frac{|R(\mathbf{k})|}{\|\mathbf{k}\|}<\epsilon \]

para suficientemente pequeños\(\mathbf{k} \neq 0\). Ya que\(R(\mathbf{0})=0\), de ello se deduce que

\[ |R(\mathbf{k})|<\epsilon\|\mathbf{k}\| \label{3.3.43} \]

para todos\(\mathbf{k}\) suficientemente pequeños. Además,\(\varphi\) es continuo en\(c\), por lo que podemos elegir lo suficientemente\(h\) pequeño como para garantizar que

\[ \mathbf{k}=\varphi(c+h)-\varphi(h) \nonumber \]

es lo suficientemente pequeño como para que (\(\ref{3.3.43}\)) se sostenga. Por lo tanto, para lo suficientemente pequeño\(h \neq 0\),

\[ \frac{|R(\mathbf{k})|}{h}<\frac{\epsilon\|\mathbf{k}\|}{h} . \]

Ahora

\[ \lim _{h \rightarrow 0} \frac{\|\mathbf{k}\|}{h}=\lim _{h \rightarrow 0} \frac{\|\varphi(c+h)-\varphi(c)\|}{h}=\|D \varphi(c)\| \]

y la elección de\(\epsilon\) fue arbitraria, por lo que se deduce que

\[\lim _{h \rightarrow \mathbf{0}} \frac{R(\mathbf{k})}{h}=0 .\]

De ahí

\[ (f \circ \varphi)^{\prime}(c)=\nabla f(\mathbf{a}) \cdot D \varphi(c) . \]

Esta es una versión de la regla de la cadena.

Teorema\(\PageIndex{4}\)

Supongamos que\(\varphi: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es diferenciable en\(c\) y\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\varphi (c)\). Entonces

\[ (f \circ \varphi)^{\prime}(c)=\nabla f(\varphi(c)) \cdot D \varphi(c) . \label{3.3.48} \]

Si imaginamos una partícula que se mueve a lo largo de la curva\(C\) parametrizada por\(\varphi\), con velocidad\(\mathbf{v}(t)\) y unidad tangente vector\(T(t)\) a la vez\(t\), entonces (\(\ref{3.3.48}\)) dice que la velocidad de cambio de\(f\) lo largo\(C\) a\(\varphi (c)\) es

\[ \nabla f(\varphi(c)) \cdot \mathbf{v}(c)=\|\mathbf{v}(c)\| \nabla f(\varphi(c)) \cdot T(c)=\|\mathbf{v}(c)\| D_{T(c)} f(\varphi(c)) . \]

En otras palabras, la tasa de cambio de\(f\) lo largo\(C\) es la tasa de cambio de\(f\) en la dirección de\(T(t)\) multiplicado por la velocidad de la partícula que se mueve a lo largo de la curva.

Ejemplo\(\PageIndex{5}\)

Supongamos que la temperatura en un punto\((x,y,z)\) dentro de una región cubica del espacio viene dada por

\[ T(x, y, z)=80-20 x e^{-\frac{1}{20}\left(x^{2}+y^{2}+z^{2}\right)} . \nonumber \]

Además, supongamos que un insecto vuela a través de esta región a lo largo de la hélice elíptica parametrizada por

\[ \varphi(t)=(\cos (\pi t), 2 \sin (\pi t), t) . \nonumber \]

Entonces

\[ \nabla T(x, y, z)=e^{-\frac{1}{20}\left(x^{2}+y^{2}+z^{2}\right)}\left(2 x^{2}-20,2 x y, 2 x z\right) \nonumber \]

y

\[ D \varphi(t)=(-\pi \sin (\pi t), 2 \pi \cos (\pi t), 1) . \nonumber \]

De ahí que, por ejemplo, si queremos conocer la tasa de cambio de temperatura para el error en\(t=\frac{1}{3}\), evaluaríamos

\[ D \varphi\left(\frac{1}{3}\right)=\left(-\frac{\sqrt{3} \pi}{2}, \pi, 1\right) \nonumber \]

y

\[ \nabla T\left(\varphi\left(\frac{1}{3}\right)\right)=\nabla T\left(\frac{1}{2}, \sqrt{3}, \frac{1}{3}\right)=e^{-\frac{121}{20}}\left(-\frac{39}{2}, \sqrt{3}, \frac{1}{3}\right), \nonumber \]

por lo

\ begin {aligned}
(T\ circ\ varphi) ^ {\ prime}\ izquierda (\ frac {1} {3}\ derecha) &=e^ {-\ frac {121} {720}}\ izquierda (-\ frac {39} {2},\ sqrt {3},\ frac {1} {3}\ derecha)\ cdot\ izquierda (-\ frac {\ sqrt {3}\ pi} {2},\ pi, 1\ derecha)\\
&=e^ {-\ frac {121} {720}}\ izquierda (\ frac {39\ pi\ sqrt {3}} {4} +\ sqrt {3}\ pi+\ frac {1} {3}\ derecha )\\
&=49.73,
\ end {alineado}

donde el valor final se ha redondeado a dos decimales. De ahí que en ese momento la temperatura para el error esté aumentando a razón de 49. 73º por segundo. También podríamos expresar esto como

\[ \left.\frac{d T}{d t}\right|_{t=\frac{1}{3}}=49.73^{\circ} . \nonumber \]

Para una formulación alternativa de la regla de la cadena, supongamos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y\(x_{i}: \mathbb{R} \rightarrow \mathbb{R}\)\(i=1,2, \ldots, n\),, son todos diferenciables y dejar\(w=f\left(x_{1}, x_{2}, \ldots, x_{n}\right)\). Si\(x_{1}, x_{2}, \ldots, x_{n}\) son todas las funciones de\(t\), entonces, por la regla de la cadena,

\ [\ begin {align}
\ frac {d w} {d t} &=\ izquierda (\ frac {\ w parcial} {\ parcial x_ {1}},\ frac {\ parcial w} {\ parcial x_ {2}},\ ldots,\ frac {\ w parcial} {\ parcial x_ {n}}\ derecha)\ cdot\ izquierda (\ frac d {x_ {1}} {d t},\ frac {d x_ {2}} {d t},\ lpuntos,\ frac {d x_ {n}} {d t}\ derecha)\ nonumber\\
&=\ frac {\ w parcial} {\ parcial x_ {1}}\ frac {d x_ {1}} {d t} +\ frac {\ w parcial} {\ parcial x_ {2}}\ frac {d x_ {2}} {d t} +\ cdots+\ frac {\ parcial w} {\ parcial x_ {n}}\ frac {d x_ {n} {d t}. \ label {}
\ end {align}\]

Ejemplo\(\PageIndex{6}\)

Supongamos que las dimensiones de una caja van en aumento de manera que su longitud, anchura y altura en el momento\(t\) sean, en centímetros,

\ [\ begin {aligned}
&x=3 t,\\
&y=t^ {2},
\ end {alineado}\]

y

\[ z=t^{3}, \nonumber \]

respectivamente. Dado que el volumen de la caja es

\[ V=x y z , \nonumber \]

la tasa de cambio del volumen es

\[ \frac{d V}{d t}=\frac{\partial V}{\partial x} \frac{d x}{d t}+\frac{\partial V}{\partial y} \frac{d y}{d t}+\frac{\partial V}{\partial z} \frac{d z}{d t}=3 y z+2 x z t+3 x y t^{2} . \nonumber \]

De ahí, por ejemplo, en que\(t = 2\) tenemos\(x = 6\),\(y = 4\), y\(z = 8\), así

\[ \left.\frac{d V}{d t}\right|_{t=2}=96+192+288=576 \mathrm{~cm}^{3} / \mathrm{sec} . \nonumber \]

Los conjuntos de gradiente y nivel

Ahora considere una función diferenciable\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y un punto\(\mathbf{a}\) en el nivel\(S\) establecido por\(f(\mathbf{x})=c\) para algún escalar\(c\). Supongamos que\(\varphi: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es una parametrización suave de una curva\(C\) que se encuentra completamente sobre\(S\) y pasa a través de ella\(\mathbf{a}\). Vamos\(\varphi(b)=\mathbf{a}\). Entonces la composición de\(f\) y\(\varphi\) es una función constante; es decir,

\[ g(t)=f \circ \varphi(t)=f(\varphi(t))=c \]

para todos los valores de\(t\). Por lo tanto, utilizando la regla de la cadena,

\[ 0=g^{\prime}(b)=\nabla f(\varphi(b)) \cdot D \varphi(b)=\nabla f(\mathbf{a}) \cdot D \varphi(b) . \]

De ahí

\[ \nabla f(\mathbf{a}) \perp D \varphi(b) . \label{3.3.53} \]

Ahora\(D \varphi(b)\) es tangente a\(C\) at\(\mathbf{a}\); además, ya que (\(\ref{3.3.53}\)) se mantiene para cualquier curva de\(S\) paso\(\mathbf{a}\),\(\nabla f(\mathbf{a})\) es ortogonal a cada vector tangente a\(S\). En otras palabras,\(\nabla f(\mathbf{a})\) es normal al hiperplano tangente a\(S\) at\(\mathbf{a}\). Así tenemos el siguiente teorema.

Teorema\(\PageIndex{5}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en una bola abierta que contiene el punto\(\mathbf{a}\), y deja\(S\) ser el conjunto de todos los puntos en\(\mathbb{R}^n\) tal que\(f(\mathbf{x})=f(\mathbf{a})\). Si\(\nabla f(\mathbf{a}) \neq \mathbf{0}\), entonces el hiperplano con ecuación

\[ \nabla f(\mathbf{a}) \cdot(\mathbf{x}-\mathbf{a})=0 \label{3.3.54} \]

es tangente a\(S\) at\(\mathbf{a}\).

Para\(n = 2\), el hiperplano descrito por (\(\ref{3.3.54}\)) será una línea tangente a una curva; para\(n = 3\), será un plano tangente a una superficie.

Ejemplo\(\PageIndex{7}\)

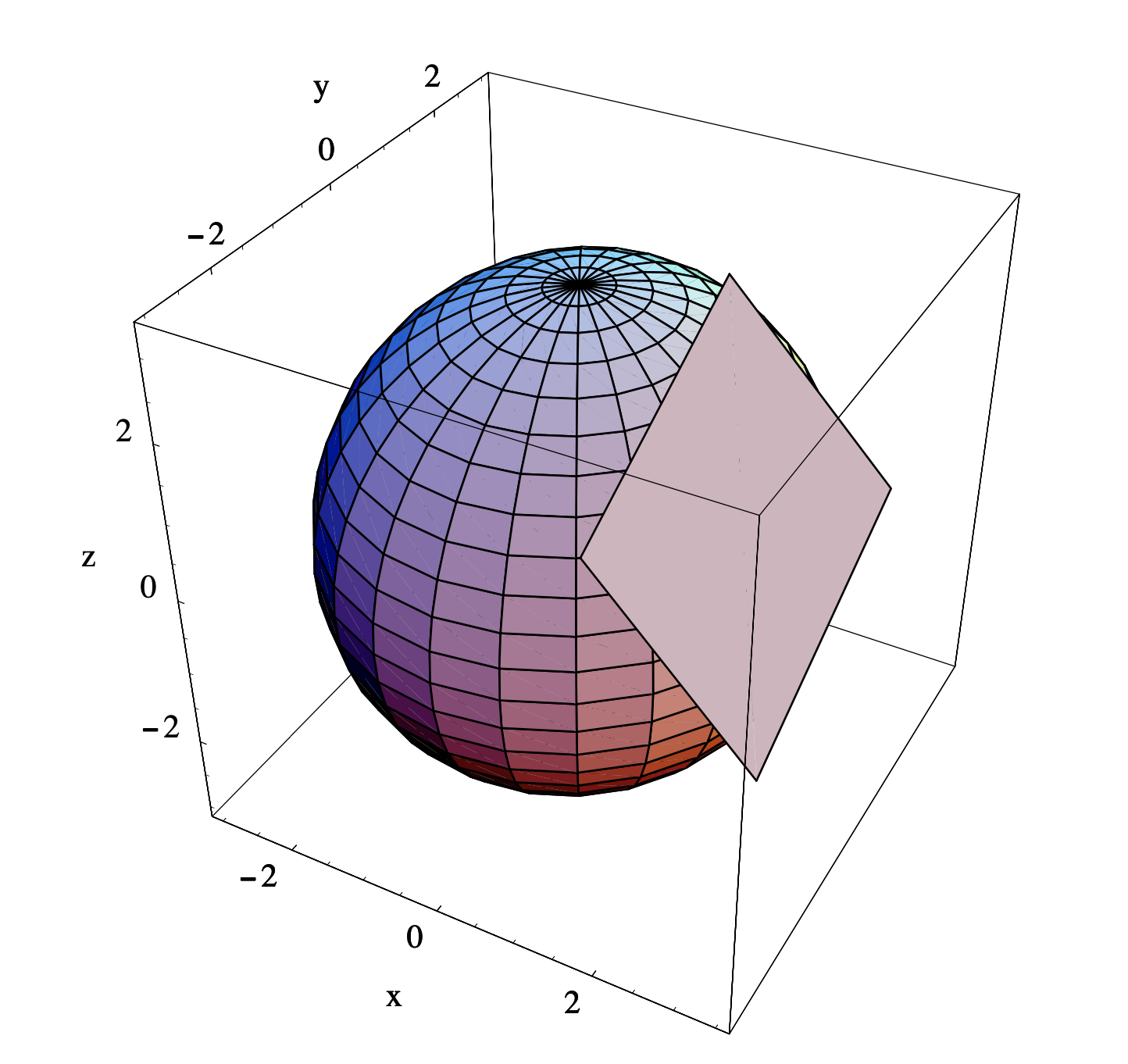
El conjunto de todos los puntos\(S\) en\(\mathbb{R}^3\) satisfacer

\[ x^{2}+y^{2}+z^{2}=9 \nonumber \]

es una esfera con radio 3 centrada en el origen. Encontraremos una ecuación para el plano tangente a\(S\) at (2, −1, 2). Primera nota que\(S\) es una superficie nivelada para la función

\[ f(x, y, z)=x^{2}+y^{2}+z^{2} . \nonumber \]

Ahora

\[ \nabla f(x, y, z)=(2 x, 2 y, 2 z) , \nonumber \]

por lo

\[ \nabla f(2,-1,2)=(4,-2,4) . \nonumber \]

Por lo tanto, una ecuación para el plano tangente es

\[ (4,-2,4) \cdot(x-2, y+1, z-2)=0 , \nonumber \]

o

\[ 4 x-2 y+4 z=18 . \nonumber \]

Ver Figura 3.3.3.

Figura\(\PageIndex{3}\): Esfera con plano tangente